空重箱混合运输条件下集装箱海运网络优化研究＊

郭子坚 王文渊 唐国磊 黄 俊

（大连理工大学水利工程学院1） 大连 116085） （交通部规划研究院2） 北京 100028）

0 引 言

随着国际海运业的发展，集装箱生成系数（集装箱吞吐量／外贸进出口总额）不断提高，适箱货物比例越来越大，集装箱运输已经逐步替代了传统的散杂货运输方式，成为世界运输发展的趋势.集装箱海运业的繁荣对其自身的经营管理模式及网络结构提出了更高要求.尤其是近年来由于国际贸易不平衡的加剧，空箱积压与调运问题逐渐成为各个航运公司发展的瓶颈.根据2007年德鲁里（Drewry）集装箱市场季度报告显示，全球集装箱港口吞吐量中空箱吞吐量约占全部集装箱总吞吐量的20%，部分港口甚至接近50%，见表1.因此，建立高效、有序的集装箱海运网络，在保证重箱运输的同时，优化空箱调运是企业降低成本、加快效率、提高收益的基础，是增进国际集装箱贸易交流的有效措施.

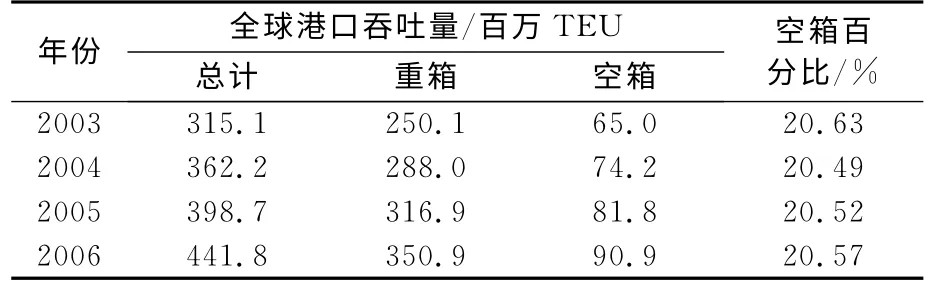
表1 全球集装箱运量及组成

针对集装箱运输网络优化及空箱调运问题，国内外学者从不同角度进行研究.Pyung等［1］提出了基于启发式禁忌搜索算法的集装箱运输网络船队管理和航线优化方法.Baird［2］针对地区性的国际集装箱港口群，提出了集疏运枢纽港的确定和优化选址方法.Shintani等［3］采用遗传算法优化集装箱班轮运输网络，并给出了空箱调运方案.卜祥智、赵泉午等［4］建立了空箱调运的集装箱海运收益管理能力分配优化模型，定量研究了不确定需求的海运集装箱能力分配问题.武振业［5］等建立了需求不确定的海运集装箱路径随机规划模型.然而，以往的研究多是针对单一航线的路径选择以及相应的空箱调运措施，对海运网络系统的全局层面的优化研究还很缺乏.宋向群等［6］针对区域性港口集装箱海上运输网络系统的最小费用流问题建立了优化模型，但在计算网络成本时，没有考虑空箱调运所产生的费用.周红梅等［7］以调运空箱成本最低为目标建立优化模型，模型中并未考虑重箱运输对空箱调运的影响.本文提出一种基于免疫算法的集装箱海运模型，同步优化港口集装箱海运网络的集装箱运输路径、空箱调运方案、集装箱船服务频率及船型配置.

1 空重箱混合运输条件下集装箱海运网络优化模型

由于航行于干线的大型集装箱船的船舶费用昂贵，所以必须选择恰当的航行路线，挂靠港不能太多，并且要求挂靠的干线港要有相当规模的箱量集中，以保证大型集装箱船有足够的满载率，体现大船的规模经济效益，从而有力地控制整个网络的航运总成本.因此，对于港口集装箱海运网络，需要寻找合理的运输线路，以使箱量在某些航线上集中，降低集装箱的单位运输成本，优化空箱调运策略，达到降低集装箱海运网络综合运输成本的目的.

1.1 集装箱综合运输成本分析

本文在集装箱海运网络运输系统的优化问题中，将集装箱综合运输成本划分为在途成本（CW）和港口成本（CP）.在途成本指在船舶航行时产生的成本，与在途时间有关；港口成本指船舶到港后产生的成本，主要与船舶吨级和装卸货物量有关，包括进港费用、装卸成本以及在港等待的时间成本等.

1）在途成本的计算 从港口i到港口j 航线上载箱量为Q（TEU）的集装箱船发生的在途成本CPij计算如下.

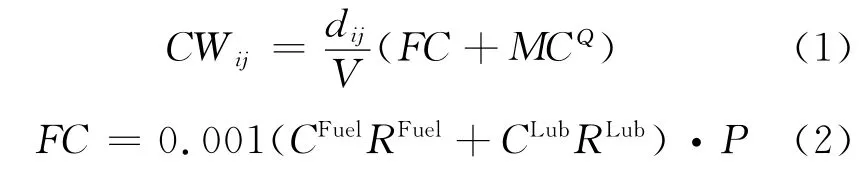
式中：dij为港口i到港口j的航行距离，n mile；V为船舶航速，kn；FC 为集装箱船每小时的燃油及相关成本消耗，美元／（h·艘）；MCQ为船舶每小时运营成本，折算为每小时的租船成本，美元／（h·艘）；CFuel为燃料成本，美元／t；RFiuel为燃料消耗，g／（kW·h）；CLub为润滑油成本，美元／t；RLub为润滑油消耗，g／（kW·h）；P 为发动机功率，kW.

2）港口成本的计算 从港口i到港口j 航线上载箱量为Q（TEU）的集装箱船发生的在途成本计算如下.

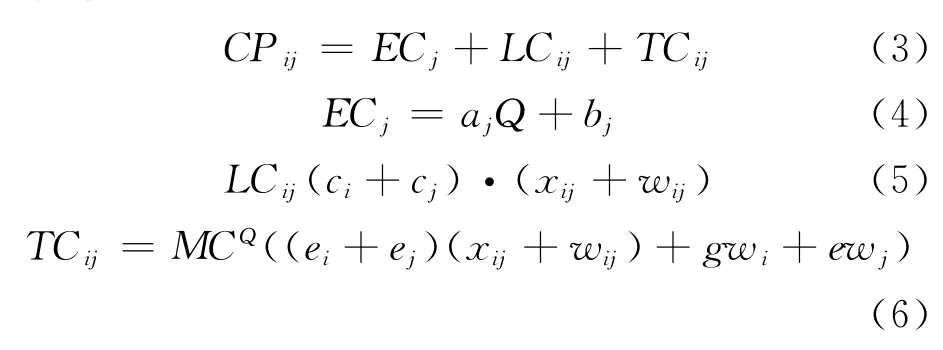
式中：ECj为船舶的进港费用，美元／艘；LCij为集装箱的装卸成本，美元／艘；TCij为船舶在港等待的时间成本，美元／艘；aj，bj为常数，与港口j 的进港费率有关；ci，cj为常数，与港口i和港口j 的单箱装卸成本；xij，wij为从i 港到j 港的重箱和空箱运量，TEU；ei，ej为分别为港口i，和港口j的装卸效率，h／TEU；gwi为i 港的出港等待时间，h；ewj为j 港的进港等待时间，h.

1.2 构建模型

设计载箱量为Q（TEU）的集装箱船，从港口i到港口j 的货运总成本为

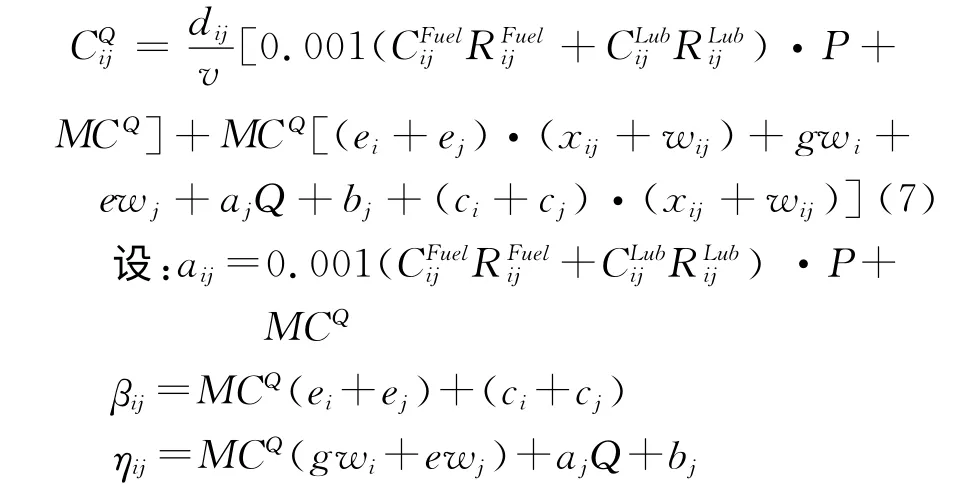
则具有N 个港口的集装箱海运网络总成本最小的优化模型为

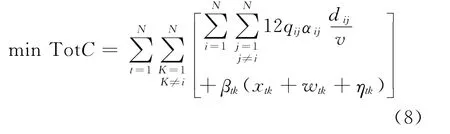
港口i到港口j 航线上的总运量为

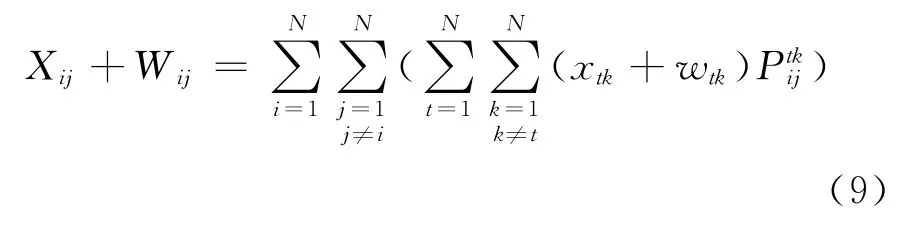
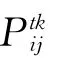
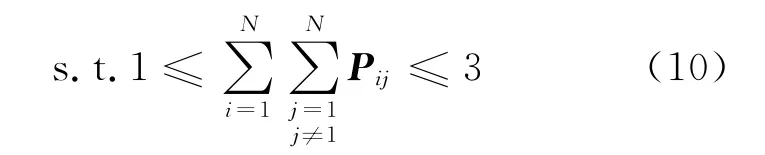
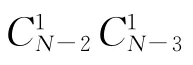
2 模型求解

2.1 免疫优化算法设计

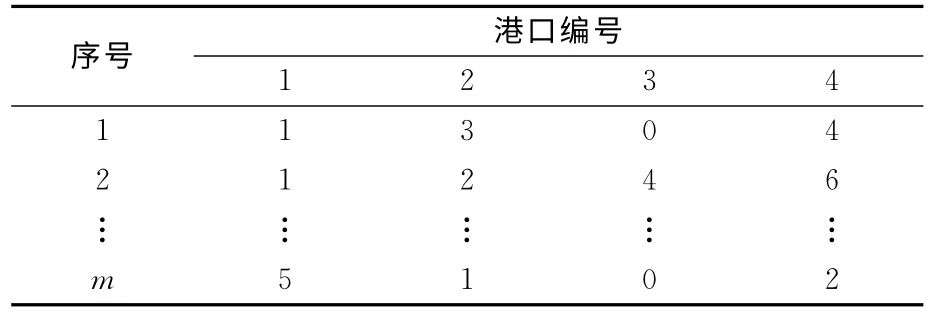
表2 二维染色体编码示例

本问题中，抗体间的亲和力：

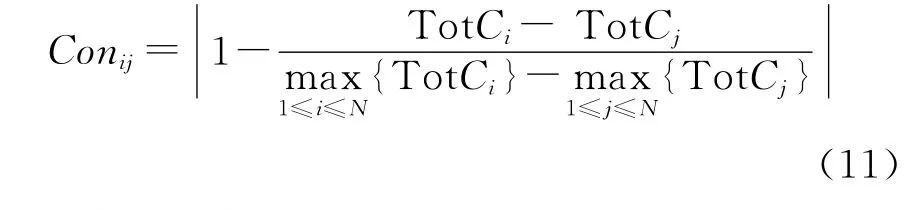
抗体与抗原的亲和力：

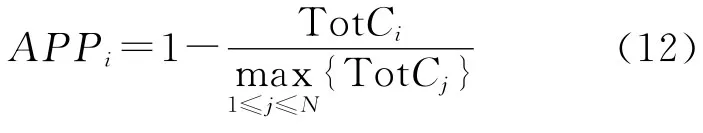
式中：Tot Ci和Tot Cj为第i个和第j 个海运网络（抗体）的总成本.

2.2 模型求解流程

决策变量Pij确定后，就可以根据总成本最小的原则确定船舶载箱量和服务频率.为简化起见，本文假定集装箱缺箱港所需集装箱均从网络内其他港口调运，不采用租赁集装箱的方式，也不从网络外的港口调运.集装箱海运网络优化流程见图1.

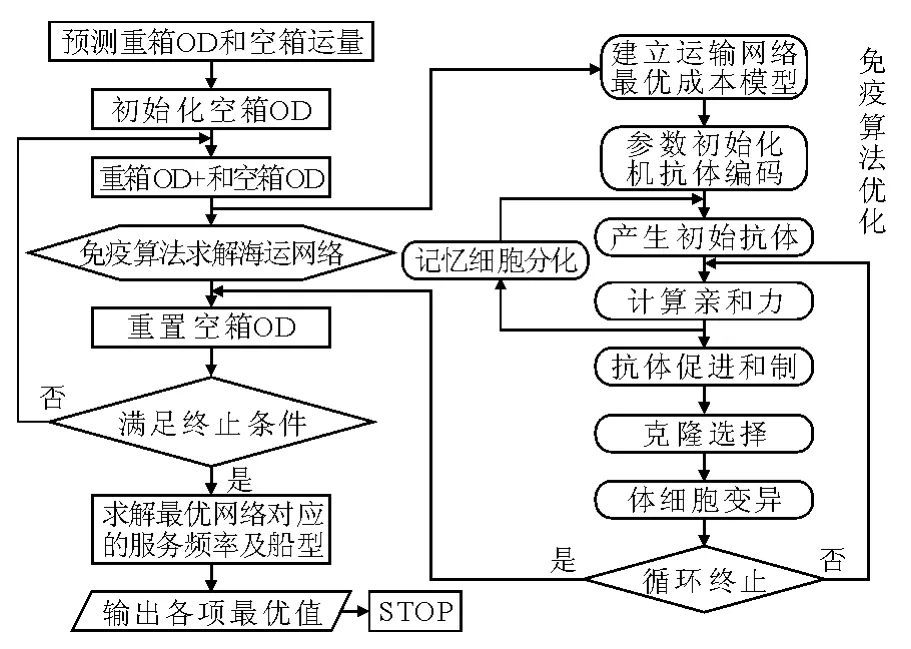
图1 集装箱海运网络优化流程图

3 算例分析

本文选择环太平洋和大西洋的8个港口，组成具有8个节点的集装箱海运网络作为研究对象.采用线性回归方法预测某船公司2015年上述8个港口间的集装箱OD 分布（origin－destination distribution），即任意2港口间的重箱生成量见表3，以及每个港口的空箱余缺量见表4.由预测结果可知，空箱运量占整个网络总运量的47%.

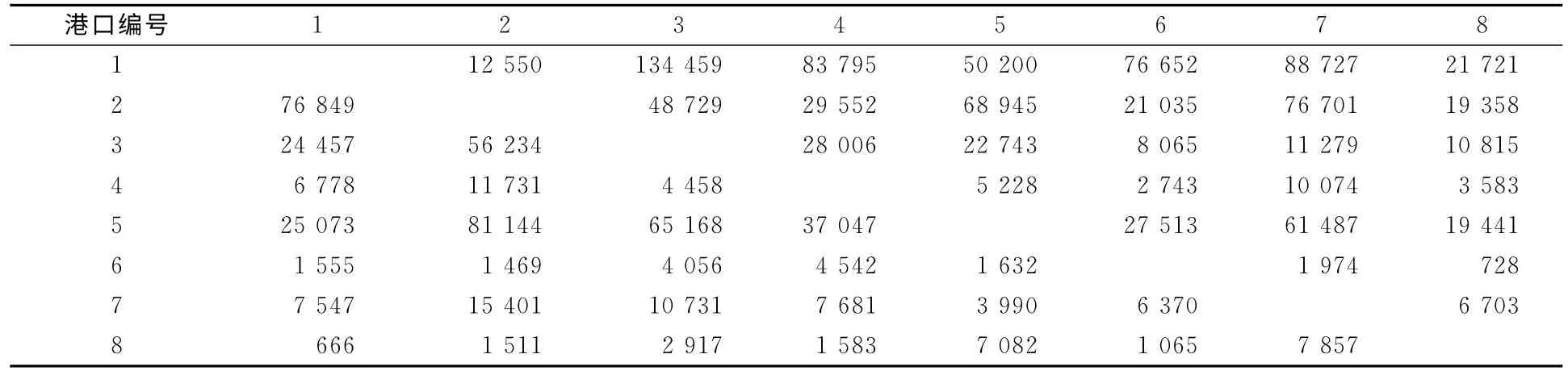
表3 某船公司2015年8个港口的集装箱OD预测表 TEU

表4 某船公司2015年8个港口的空箱运量预测表TEU

根据集装箱海运网络的优化模型，采用C＋＋语言编写优化程序，并在VC＋＋6.0环境下通过编译运行.由于某些集装箱船型的基本运营数据难以获得，无法为其建立基于最优成本的运输网络模型，因此仅选用Q＝｛500，1000，2500，3500｝5种设计载箱量的集装箱船（集装箱船参数见表5）作为网络中运营的船型.

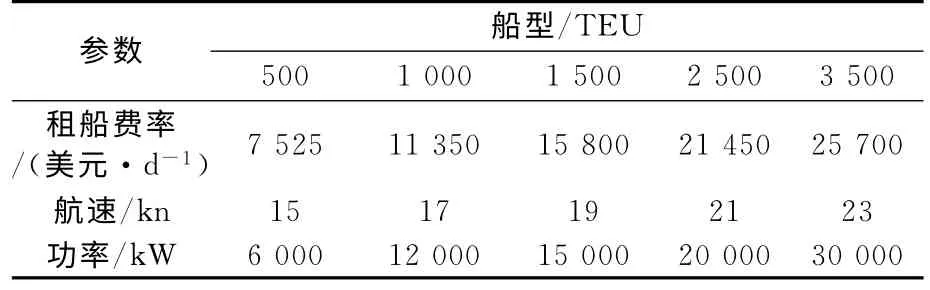
表5 集装箱船参数

经过反复实验，算法最优参数选择如下：抗体群规模PN＝500；记忆细胞数量MCM＝40；抗体群最终进化代数TEM ＝200；变异率PM ＝0.03；亲和力阈值TAC＝0.85.输入数据，运行程序得海运网络优化结果见表6.相应的集装箱海运网络中转方案见表7，空箱运输的OD 调运方案见表8，船型及服务频率配置分别见表9、表10.

表6 集装箱海运网络优化结果 百万美元

表7 最优解对应的集装箱海运网络中转方案

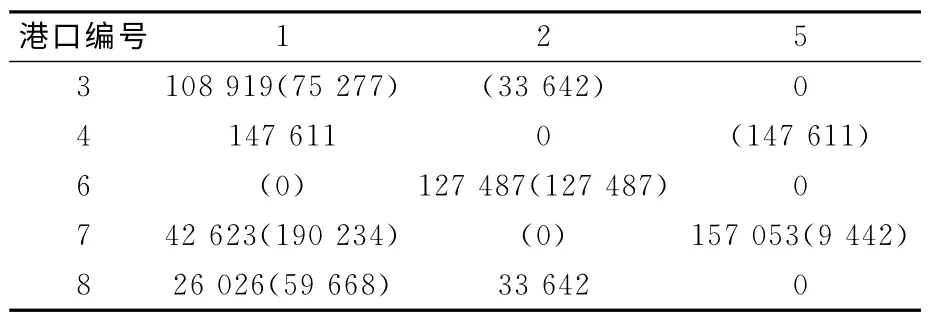
表8 2种不同的空箱OD调运方案比较

表9 最优解对应的船型优选方案 TEU

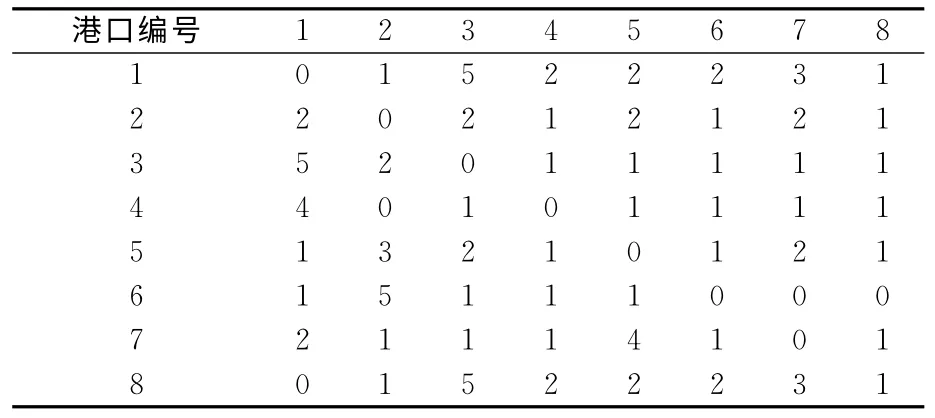
表10 最优解对应的服务频率配置 艘／月

由表10可知，对于一个航运公司来说，因其运力有限，服务频率配置方案中有27个服务频率为1艘／月，占运量个数的53%.这种情况下，最好能采取与其他船公司的集装箱拼船的策略以降低成本.

4 结束语

由表6 可知，空箱运输网络最优成本为781.94百万美元，比全部OD 量均采用直达方式运输节约3.02%，24.35百万美元.

由表7可知，在由8个港口组成的海运网络中，仅有4个运量需要从其他港口中转，而大多数运量均选择直达的方式运输.作为中转港的港口仅有一个5号港，该港口不仅位于网络的中心区域，港口自身具有较大的运量，因此，有条件成为该海运网络中的枢纽港.

表8是分别按最短运距优选调运原则和最低成本优先调运原则确定的空箱OD 调运方案，由表8可知，简单的将积压的空箱往最近的缺箱港运输并不是合理的作法，航运企业完全可以通过完善的管理来节约这部分成本.

由表9可知，该集装箱海运网络的51条航线中，有30 条航线上的集装箱船载箱量在2500 TEU 以上，且载箱量为3500TEU 的集装箱船均在远洋干线中使用.

考虑空重箱混合运输条件的集装箱海运网络优化方法是解决空箱调运问题的关键所在.本研究引入基于二维染色体编码的免疫优化算法，在建立空重箱混合运输条件下集装箱海运网络优化模型的基础上，实现了集装箱海运网络集装箱运输路径、空箱调运方案、集装箱船舶服务频率及船型配置的同步优化.通过数值计算方法验证了模型的有效性，并指出空箱OD 应从全局的角度出发，合理调运，而不是简单的将积压的空箱运往最近的缺箱港.同时，有效地验证了在规模经济效益的驱动下，对于长距离运输，大型集装箱船更具有成本优势.

［1］PYUNG H K，WOON S L，DONG W J.Fleet sizing and vehicle routing for container transportation in a static environment［J］.OR Spectrum，2004（26）：193－209.

［2］BAIRD A J.Optimising the container transhipment hub location in northern Europe［J］.Journal of Transport Geography，2006，14（3）：195－214.

［3］SHINTANI K，IMAI A，NISHIMURA E，et al.The container shipping network design problem with empty container repositioning［J］.Transportation Research Part E，2007（43）：39－59.

［4］卜祥智，赵泉午，黄 庆，等.考虑空箱调运的集装箱海运收益管理能力分配优化模型［J］.中国管理科学，2005，13（1）：71－75.

［5］武振业，宋天生，赵 柯.海运集装箱运输路径选择［J］.西南交通大学学报，2006，41（3）：269－272.

［6］宋向群，张 鹏，郭子坚.基于蚁群算法的港口集装箱运输网络径流优化［J］.大连理工大学学报，2007（6）：853－857.

［7］周红梅，方 芳.航运集装箱空箱调运优化模型的研究［J］.武汉理工大学学报：交通科学与工程版，2003，27（3）：384－387.

［8］黄 俊，宋向群，郭子坚.基于二维染色体编码的集装箱海运网络免疫算法优化模型［J］.土木工程学报，2007，40（8）：94－99.