一种求解高维多模态复杂问题的差分文化算法*
拓守恒,陶维天
(1.陕西理工学院数学与计算机科学学院,陕西 汉中 723000;2.甘肃中医学院网络中心,甘肃 兰州 730000)
1 引言
随着人工智能技术的发展,许多科学和工程领域大规模复杂难题得到了很好的解决,但更加复杂多维优化问题随之出现,需要学者们不断探索更好的优化处理方法。近10年来仿生智能优化算法成为学者们的研究热点,例如遗传算法GA(Genetic Algorithm)、微粒群优化算法、差分进化算法、蚁群算法和文化算法 CA(Cultural Algorithm)[1]等。文化算法是Reynolds于1994年提出的一种模拟文化进化过程的智能优化算法。文化算法通过不断地从种群进化过程中积累经验知识,然后再利用积累的经验知识去指导种群的进化,从而能够有效提高算法的收敛性。该算法很适合大规模复杂系统的优化处理,已成功应用于大规模空间数据库的数据挖掘、非线性约束优化[2]、多目标优化和机器学习等问题的处理。
2 文化算法及研究现状
文化算法由种群空间(Population Space)、信度空间(Belief Space)和交流渠道(Communication Channel)构成,交流渠道通过三个函数(接受函数Acceptance Function、影响函数Influence Function和更新调整函数Adjust Function)完成。文化算法的框架如图1所示,种群空间和信度空间是两个独立的进化空间,彼此按照通信协议(Communication Protocol)进行联系。
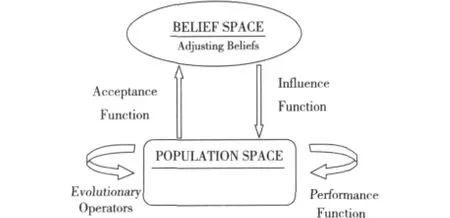
Figure 1 Cultural algorithm framework图1 文化算法的基本框架
下面是算法的基本过程:
算法1 文化进化算法


由图1和算法1可以看出,文化算法只是给出了一个进化框架,并没有对种群空间和信度空间的进化过程进行具体要求和描述,因此研究者是通过将一些仿生智能优化算法与文化算法结合来进行具体问题的处理。文献[3]中Becerra等将差分进化引入文化算法的种群空间,成功解决了非线性约束优化问题。文献[4]将模拟退火算法引入到文化算法中,实现了移动代理网络路由优化。文献[5]将免疫量子进化算法引入文化算法中,采用量子进化算法对种群空间进行优化,信度空间采用免疫接种技术。黄海燕等提出了一种基于多层信念空间的文化算法[6],通过对多层信念空间的择优选用将提取的知识用于提高进化计算性能,解决约束优化问题。高丽丽等提出一种基于文化算法的粒子群优化算法[7],在群体空间采用基于高斯概率分布和柯西概率分布的改进PSO算法,在信念空间根据形势知识和规范化知识指导种群的进化。郭骥等提出一种基于文化算法和高斯变异的多群协同粒子群算法[8],用于求解高维多峰函数寻优问题。郭一楠等[9]对文化算法的结构、研究现状和发展趋势作了详细的分析。
本文针对高维多模态优化问题,提出一种基于差分进化和高斯分布估计的小生境文化进化算法模型,算法在种群空间中利用改进的差分进化算法进化种群,将获得的小生境传送到信度空间。在信度空间中,利用高斯分布算法求解每个小生境的最优解,将小生境特征存储记录下来作为进化知识,然后用进化知识库再去指导种群空间进行搜索。
3 关键技术
3.1 自适应差分进化算法
差分进化算法 DE(Differential Evolution)[10]是由Storn和Price提出的一种用于优化问题的启发式算法。该算法采用实数编码,模仿生物进化过程中“优胜劣汰,适者生存”的原理,通过对个体进行方向扰动来达到使个体函数值下降的目的,对函数的可导性甚至连续性没有要求,适用性很强。DE算法的优点是实现简单、参数少、全局优化能力强,在求解高维复杂优化问题时收敛速度快;其缺点是求解精度低。本文提出一种自适应差分变异进化算法,自适应变异操作是由随机产生的二进制串ri= {s1,s2,…,sD}与变异向量对应属性进行点乘,变异频率随着进化代数的增加逐步减小。
算法2 自适应差分进化算法

其中,λ和F是缩放因子,在区间[0,2]内取值,用于控制差分向量的扰动大小。rand(1,D)表示随机产生一个D维的向量,每一维的值是(0,1)之间的随机数。c=0.9-0.3t/T是差分自适应变异因子,用于控制二进制向量rd中1的个数,随着c的值从0.9逐步递减到0.6,rd中1的个数比例(c-0.5)从40%递减到10%。其实,rd中1的个数比例就是差分变异概率。这样算法在进化初期具有较大的变异概率,具有较强的差分扰动能力,随着进化的深入,为了避免算法陷入停滞,算法通过逐步降低变异概率,保证算法的扰动能力,并且能够逐步提高解的精度。算法时间复杂度为O(N),函数评价次数为N次。显然,算法通过对个体的各维变量同时并行变异,不会随着函数维数的增加而增加算法的时间复杂度和函数评价次数,适用于高维优化问题。
虽然该差分进化算法用于高维复杂问题时,不会随着维度的增加而增加时间复杂度,收敛速度快,但同时也存在求解精度低的问题。因此,本文利用小生境技术和高斯分布估计优化算法进行小生境内局部搜索,有效地解决了精度问题。
3.2 高斯分布估计优化算法
分布估计算法EDA(Estimation of Distribution Algorithms)[11,12]通过概率模型来分析变量的关系,并根据当前种群的分布状况来产生下一代种群。EDA的基本步骤有:
(1)建立解空间的概率模型。模型对当前种群进行评估并构建优秀个体解集来描述群体的分布概率模型。
(2)根据(1)构建的概率模型产生下一代种群。
分布估计算法用于高维复杂优化问题时能够有效地降低时间复杂度,收敛速度快,求解精度高。本文采用高斯分布估计优化算法GEDA(Gaussian Estimation of Distribution Algorithms)在一个小生境局部的范围内获得局部最优解。高斯分布估计搜索算法的具体描述如下:
算法3 高斯分布估计优化算法

其中,α∈ (0,1),β∈ (0,1)为 学 习 因 子,xbest,j、xworst,j分别表示跟种群中最优个体和最差个体所对应的第j维的属性值。
3.3 动态小生境识别算法
小生境(Niche)在生物学中是指特定环境下的一种生存环境。生物在其进化过程中,一般总是和与自己相同的物种在某一特定的地理区域中生活在一起,共同繁衍后代。小生境技术的基本思想是将生物学中的小生境概念应用于进化计算中,将进化计算中的每一代个体划分为若干类,每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个群,再在种群中,以及不同种群中之间,杂交、变异产生新一代个体群。
在小生境识别技术中,如何确定小生境半径的大小是一个难点问题,往往需要先给出确定的半径然后再去确定小生境个数。这样,若小生境半径设置过大,虽然有利于保持种群多样性,但种群进化速度缓慢;若小生境半径设置过小,虽然有利于提高算法的收敛速度,但种群多样性缺失较快,算法容易早熟而陷入局部最优[13,14]。作者在文献[13]中根据种群中个体适应值和个体相似度提出一种动态小生境识别算法,能够准确有效地获得小生境的大小特征。
4 基于差分进化和高斯分布估计的文化进化算法模型
4.1 算法模型
由于传统的优化算法在求解高维多模优化问题时,收敛速度慢、稳定性差、求解精度低和容易陷入局部搜索,本文将差分进化算法和高斯分布估计算法引入到文化算法模型中,将差分进化和高斯分布估计算法融合,利用文化算法的智能引导来提高算法的性能。算法描述如下。
算法4 基于差分进化和高斯分布估计的文化进化算法
(1)设置初始参数。
(2)种群空间进行种群的初始化,并评价其适应值。
(3)利用自适应差分进化算法对种群进行Tn代进化。
(4)利用动态小生境识别算法识别出种群空间中的小生境种群。
(5)接收函数Accept()将小生境种群送至信度空间。
(6)在信度空间,对每个小生境种群采用高斯分布估计优化算法进行境内最优解搜索,记录每个小生境的大小(u,δ)和境内最优解,并放入进化知识库中。
(7)采用影响函数Influence()对种群空间中的种群进行选择:选择不属于进化知识库中小生境内的个体直接进入下一代(消去种群空间内的小生境,避免以后对该区域进行重复密集搜索)。
(8)随机产生新个体,如果其不在知识库的某一小生境内,将其加入种群中,重复该步骤,直到满足种群规模大小。
(9)如果满足终止条件,则结束运行并输出信度空间进化知识库内的最优解;否则,转(3)进行下一代进化。
基于差分进化和高斯分布估计的文化进化算法模型如图2所示。
4.2 算法分析

Figure 2 Cultural algorithm model based on DE and Gaussian distribution algorithm图2 基于差分进化和高斯分布估计的文化进化算法模型
利用小生境技术和高斯分布估计优化算法进行小生境内局部搜索,虽然能够有效地解决精度问题,但频繁利用小生境识别算法和高斯分布估计算法需要付出巨大的时间代价。为了解决该问题,在种群空间中利用算法2进行Tn代的进化后再去识别小生境,一个小生境就对应多峰值函数的一个峰值。将获得小生境空间大小存入信度空间的进化知识库。进化知识库根据库内小生境的位置和特征将该小生境(峰值)削平,避免了种群再次陷入该区域进入重复搜索。并且通过进化知识库的指导来选择和产生新一代种群,能够保证种群的多样性。
5 仿真分析
为了评估本文算法的性能,选取了四个复杂高维的多峰值Benchmark函数(f1:Rastrigin;f2:Ackley;f3:Griewangk;f4:Rosenbrock)进行测试。在四个函数中f1~f3属于多峰值函数,存在多个极值点;函数f4被称作变态函数,变量之间具有很强的关联性,最优解是(1,1,…,1),最优函数值为0,但该函数在优化时,非常容易收敛于点(0,0,…,0)。四个函数的具体表达式如下:
Rastrigin:


实验测试结果分别与混沌差分文化算法(CDECA)[15]和取得较好优化效果的改进差分算法Defir DE[16]进行了比较和分析。
5.1 运行环境与参数设置
在测试中,使用微机硬件环境为华硕笔记本电脑,I3 450CPU,1 GB内存,在 MATLAB 2009(a)软件平台上进行编程实现。
设置种群空间中种群规模N=100,差分进化算法中缩放因子λ=0.4,F=0.6;高斯分布式估计算法中学习因子α=0.5,β=0.5;在100和200维时,设置函数f1~f3的最大进化代数为T=1 000,最高评价次数为300 000次,设置函数f4的最大进化代数为3 000,最高评价次数为1 000 000次,在500维时,设置最大进化代数为T=5 000,函数最高评价次数为1 500 000次。
5.2 运行结果与分析
在所有测试函数中,让程序各自独立运行20次,记录最优值 (Best)、平均值(Mean)、最差值(Worst)和标准差(Std.Dev),统计结果如表1所示。
由表1可以看出,本文算法对每个函数进行的20次独立测试中,除了f4函数在500维时平均最优解的精度不够高外,其它函数都获得了高精度全局最优解。图3中显示了变态函数f4在100,200,500维时的进化曲线。可以看出,在100维和200维时,算法能够在1 000代进化以内发现最优解,在500维时,收敛速度稍低,但也能够在5 000代进化后发现最优解并逐步收敛。

表2中,在维数为100和200时,将本文算法和CDECA、Defir DE的平均最优解进行了比较。结果可以看出,对所有函数f1~f4,在同等条件下,本文算法的平均最优解精度都明显高于CDE-CA和Defir DE算法。从图4中的函数收敛曲线可看出,对于函数f4,本文算法能够很快地收敛到4 000以内,并能够一直基本保持下降收敛状态。由于CDECA和DefirDE算法在优化初期为了在整个搜索空间探测全局最优解,收敛速度较慢,在进化次数达到2 000代以后,才进入局部搜索,但限于局部搜索算法的求解精度不高,从而导致全局最优解不如本文算法好。

Table 1 Experimental results of the proposed algorithm in this paper表1 本文算法的测试结果

Table 2 Mean optimal solution comparison of three algorithm(proposed algorithm,CDECA,Defir DE)表2 本文算法和CDECA,DefirDE的平均最优解比较
6 结束语
首先阐述文化算法的基本框架和原理,分析了文化算法的发展现状。根据文化算法的结构特征,将差分进化算法和高斯分布算法应用到文化算法中。在种群空间中,利用自适应差分进化算法在可行域内进行全局的并行搜索。采用小生境识别算法识别小生境种群,将生成的小生境种群送至信度空间并用高斯分布估计算法进行境内优化,并将优化结果放入进化知识库,进化知识库通过Influence函数指导种群空间进行搜索。算法能够有效地避免种群在一些局部区域重复搜索。最后通过四个高维Benchmark函数测试表明,本文算法具有全局搜索能力强、收敛速度快、求解精度高和稳定性好等优势。
[1]Reynolds R G.An introduction to cultural algorithms[C]∥Proc of the 3rd Annual Conference on Evolutionary Programming,World Scientific,1994:131-139.
[2]Reynolds R G,Michalewicz Z,Cavaretta M.Using cultural algorithms for constraint handling in GENOCOP[C]∥Proc of the 4th Annual Conference on Evolutionary Programming,1995:298-305.
[3]Becerra R L,Coello C A C.Culturizing differential evolution for constrained optimization[C]∥Proc of the 5th Mexican In-ternational Conference in Computer Science,2004:304-311.
[4]Ma Jun,Zhang Jian-pei,Yang Jing,et al.Research on cultural algorithm for solving routing problem of mobile agent[J].The Journal of China Universities of Posts and Telecommunications,2008(4):121-125.
[5]Liu Sheng,Yu Xing.A cultural immune quantum evolutionary algorithm and its application[C]∥Proc of Asia Simulation Conference 2008/the 7th International Conference on System Simulation and Scientific Computing,2008:1.
[6]Huang Hai-Yan,Gu Xin-Sheng,Liu Man-Dan.Research on cultural algorithm for solving nonlinear constrained optimization[J].Acta Automatica Sinica,2007,33(10):1115-1120.(in Chinese)
[7]Gao Li-li,Liu Hong,Li Tong-xi.Particle swarm based on cultural algorithm for solving constrained optimization problems[J].Computer Engineering,2008,34(5):179-181.(in Chinese)
[8]Guo Ji,Peng Xin,Ma Lin-hua.Particle swarms cooperative mutative optimization algorithm combining cultural algorithm[J].Computer Engineering and Applications,2011,45(16):46-48.(in Chinese)
[9]Guo Yi-nan,Wang Hui.Overview of cultural algorithms[J].Computer Engineering and Applications,2009,45(9):41-46.(in Chinese)
[10]Storn R,Price K.Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359.
[11]Zhou Shu-de,Sun Zeng-qi.A survey on estimation of distribution algorithms[J].Acta Automatica Sinica,2007,33(2):113-124.(in Chinese)
[12]Zhang Jian-hua,Zeng Jian-chao.Estimation of distribution algorithms using empirical distribution function as probability model[J].Computer Engineering and Applications,2011,47(8):33-35.(in Chinese)
[13]Tuo Shou-heng,Wang Wen-yong.Self-adaptive differential evolution algorithm based on orthogonal and niche elite for high-dimensional multi-modal optimization[J].Journal of Computer Applications,2011,31(4):1094-1098.(in Chinese)
[14]Lu Qing,Liang Chang-yong,Yang Shan-lin.An adaptive niche genetic algorithm for multimodal function optimization[J].Pattern Recognition and Artificial Intelligence,2009,22(1):91-100.(in Chinese)
[15]Lu You-lin,Zhou Jian-zhong.Differential evolution-based cultural algorithm combined with chaotic search and its application[J].Journal of System Simulation,2009,21(16):5107-5111.(in Chinese)
[16]Noman N,Iba H.Enhancing differential evolution performance with local search for high dimensional function optimization[C]∥Proc of 2005 Conference on Genetic and Evolutionary Computation(GECCO 2005),2005:967-974.
附中文参考文献:
[6]黄海燕,顾幸生,刘漫丹.求解约束优化问题的文化算法研究[J].自动化学报,2007,33(10):1115-1120.
[7]高丽丽,刘弘,李同喜.基于文化粒子群算法的约束优化问题求解[J].计算机工程,2008,34(5):179-181.
[8]郭骥,彭鑫,马林华.结合文化算法的多种群协同变异PSO算法[J].计算机工程与应用,2011,45(16):46-48.
[9]郭一楠,王 辉.文化算法研究综述[J].计算机工程与应用,2009,45 (9):41-46.
[11]周树德,孙增圻.分布估计算法综述[J].自动化学报,2007,33(2):113-124.
[12]张建华,曾建潮.经验分布函数概率模型的分布估计算法[J].计算机工程与应用,2011,47(8):33-35.
[13]拓守恒,汪文勇.求解高维多模优化问题的正交小生境自适应差分演化算法[J].计算机应用,2011,31(4):1094-1098.
[14]陆青,梁昌勇,杨善林,等.面向多模态函数优化的自适应小生境遗传算法[J].模式识别与人工智能,2009,22(1):91-100.
[15]卢有麟,周建中,李英海,等.混沌差分文化算法及其仿真应用研究[J].系统仿真学报,2009,21(16):5107-5111.
TUO Shou-heng,born in 1978,MS,lecturer,CCF member(E200020808M),his research interests include evolutionary computation,artificial intelligence,and neural network.

陶维天(1976-),男,甘肃兰州人,硕士,讲师,研究方向为计算机应用和医学信息学。E-mail:lztao@126.com
TAO Wei-tian,born in 1976,MS,lecturer,his research interests include com-puter applications,and medical informatics.

——以贵阳花溪公园为例

