无线传感器网络离群时间序列检测研究*

唐 琪，刘学军

(南京工业大学电子与信息工程学院，南京211816)

传感器网络[1]是由大量小型的、低成本和低功耗的传感器节点组成，传感器节点采集的异常数据称为离群数据，这些离群数据往往代表某种异常事件的发生，例如火灾的出现、入侵监测[2]，攻击异常检测[3]等。因此，在监测系统中，传感器节点的离群数据往往更重要，也常常是监测的重点。离群数据检测的基本算法有基于统计[4]的离群数据检测方法，基于偏离的离群数据检测方法，基于距离[5]的离群数据检测方法和基于密度[6]的离群数据检测方法等等。离群数据检测包括单个离群数据点的检测和时间序列离群数据的检测，通常后者的复杂度远远高于前者。在无线传感器网络中，每个传感器节点采集到的数据可以认为是一个时间序列，而所有传感器节点采集到的数据被认为是一个时间序列数据集，通过时间序列进行离群数据检测比单个离群数据点检测往往更有意义，更有利于揭示异常事件的发生。但是，时间序列异常检测算法的复杂度通常都很高，难以应用于无线传感器网络环境中。因此，本文通过将时间序列转换成切比雪夫多项式，通过少数切比雪夫系数的比较来快速判断两个时间序列数据的相似性，从而发现异常的时间序列。该算法不仅适用于一维时间序列，也适用于多维时间序列。

本文后续内容安排如下:第1节介绍了相关的研究工作;第2节提出了一种基于切比雪夫多项式的无线传感器网络离群时间序列检测算法;第3节通过实验分析了无线传感器网络时间序列离群数据检测算法的性能;第4节总结了全文。

1 相关研究

在无线传感器网络中，离群时间序列是那些与其他时间序列有较大偏差的时间序列，以至于引起这样的怀疑，这些偏差并非随机产生，而是产生于一种完全不同的方式。研究表明，利用切比雪夫系数的欧氏距离判定两个时间序列的相似度，相对于离散傅里叶变换(Discrete Fourier Transform，DFT)[7]，离散小波变换(DiscreteWaveletTransform，DWT)[8]，自适应分段常数近似(Adaptive Piecewise Constant Approximation，APCA)[9]，分段聚合近似(Piecewise Aggregate Approximation，PAA)[10]，前者的算法精确度高于后面几种算法。Yang Zhang[11]等人对传感器网络的离群点检测技术进行了综述，详细地分析了传感器网络中离群点检测的意义、应用领域以及相关算法等。Dang-Hoan Tran[12]等人提出了在无线传感器网络中利用DFT方法进行离群数据检测，通过将时间序列转变成频域序列进行离群数据检测。Yongzhen Zhuang[13]等人提出了在无线传感器网络中网络异常清洗方法，通过对时间序列进行小波变换来检测离群数据。ShengBo[14]等人提出了基于直方图的离群点检测研究算法，但是只适合一维数据，不适合多维数据。Kifer[15]等人提出了一种复杂的无参框架的离群数据检测，适用于一维数据流，不适合高维数据流。

与以上研究不同，本文基于切比雪夫思想和欧氏距离，提出了一种新的快速无线传感器网络离群时间序列检测算法(fast outlier time series detection algorithm，FODA)。

2 离群时间序列检测算法FODA

2.1 网络模型

本文要解决的问题是传感器节点采集到的低维或高维数据构成的时间序列，通过切比雪夫思想快速检测出离群时间序列，具体描述如下:

在无线传感器网络Y中，N个无线传感器节点部署在区域D内，Y=(A，E)。A表示网络中的传感器节点集合A={Ai，i=1，…N}，E表示两个在彼此通信范围内的相连传感器节点的虚拟边。传感器节点采集到的数据是一个长度为m，维数为d的多变量时间序列，存储到时间窗口W中。将长度为ω的滑动窗口ω＜＜m放在时间序列的起始位置，此时滑动窗口对应时间序列上长度为ω的一段基本窗口，然后滑动窗口向后移，以时间序列的第2点为起始点，形成另一个长度为ω的基本窗口，依此类推，共得到m－1个长度为ω的基本窗口，这些基本窗口用S=(S1，S2，…，Sm－1)表示。本文利用滑动窗口、基本窗口检测出离群时间序列。无线传感器网络结构如图1所示。增大滑动窗口每次移动的距离，可以减少基本窗口的数量。

图1 无线传感器网络结构

2.2 切比雪夫思想的基本概念

本节回顾了切比雪夫多项式的正交性和切比雪夫系数的计算。

定义1切比雪夫多项式[16]:切比雪夫多项式Pm(t)=cos[mcos(－1)(t)]，其中 t∈[－1，1]。因为cosmθ+cos(m－2)θ=2cosθcos(m－1)θ，切比雪夫多项式可以改写为

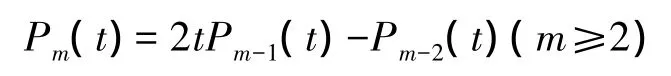
如:P0(t)=1，P1(t)=t，P2(t)=2t2－1，P3(t)=4t3－3t，P4(t)=8t4－8t2+1

定义2设 t=cosθ，则 Pi(cosθ)=cos(iθ)，Pj(cosθ)=cos(jθ)。两个切比雪夫的内积:

定义3给定切比雪夫多项式P0，…，Pm，将函数f(t)近似为:

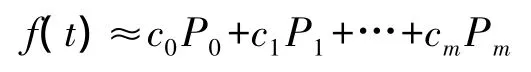
切比雪夫多项式系数[17]:

2.3 时间序列的切比雪夫思想

定义4时间序列的切比雪夫逼近:时间序列 S={(t1，v1)，…，(tω，vω)}，其中－1≤t1＜…＜tω≤1(把时间标准化为[－1，1])。时间序列是一个离散函数，将离散函数化成连续函数，即:

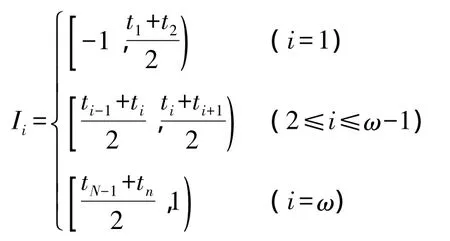
那么 g(t)=vi，其中 t∈Ii(1≤i≤ω)。将时间序列转换成的连续函数为，其中 t∈Ii(1≤i≤ω)。

时间序列的切比雪夫系数:

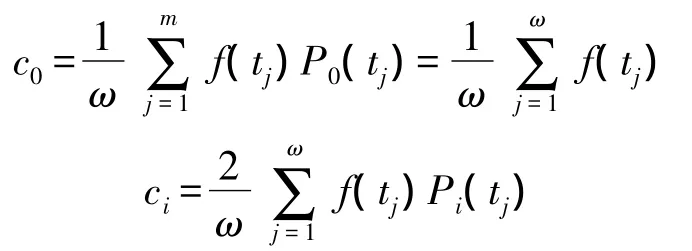
定义5长度均为ω的两个一维时间序列为S1={(t1，v1)，…，(tω，vω)}和 S2={(t1，q1)，…，(tω，qω)}，两个时间序列的欧氏距离:

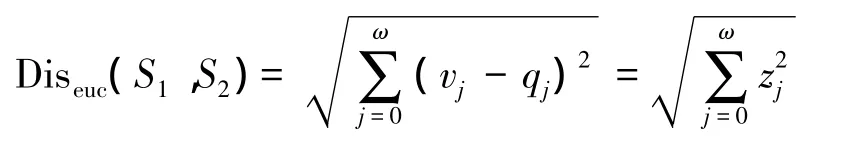
定义6长度均为ω的两个一维时间序列S1，S2的连续函数分别为f1(t)和f2(t)且fZ(t)=f1(t)－f2(t)，切比雪夫系数向量分别为和(T 为向量 C 的转置)，两个系数向量的欧式距离:

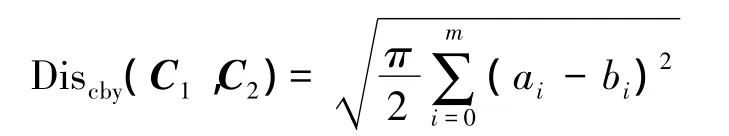
引理1Discby(C1，C2)≤Diseuc(S1，S2)。

证明

其中第二步由文献[16]得到。

定义7d维的两个时间序列S，R的切比雪夫向量系数分别为。两个时间序列的切比雪夫向量系数的欧氏距离为:

根据引理1 得 Discby(C，D)≤Diseuc(S，R)。

定义8相似序列:对于两个时间序列S，R，此两个时间序列的切比雪夫系数向量分别为C，D。若Discby(C，D)＜ε，则称时间序列S和R相似。记为similar(S，R)。进行相似度匹配时，我们采用滑动窗口机制，找出新数据窗口(滑动窗口)和历史数据窗口(基本窗口)的相似度，并计算出相似度值。

定义9对于一个时间序列S，如果历史数据窗口中，与之相似的时间序列数量小于一定的比例，那么时间序列S称为离群时间序列即

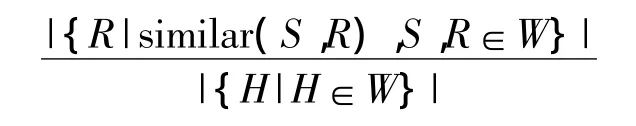
其中R为与S相似的时间序列，H为时间窗口W中的历史数据窗口。

2.4 算法描述

(1)算法步骤详述

每个传感器节点采集数据构成一个时间序列，在时间窗口中通过切比雪夫思想把时间序列化成时间区间在[－1，1]的连续函数，并计算连续函数的切比雪夫多项式系数，利用系数求两个时间序列的相似度，最后利用定义9判定离群时间序列，将离群时间序列传给Sink节点。

(2)算法伪代码

将各个传感器节点的离群时间序列传给Sink节点

3 算法实验分析

在100×100的区域内随机部署101个传感器节点(包括基站)。在无线传感器网络中，相对于数据无线发送接收来说，节点进行计算和储存的能耗基本可以忽略不计，网络的生存时间主要取决于数据传输。设节点初始能量为1 J，发送和接收能耗均为0.395 nJ/bit，空闲能耗为 0.039 nJ/bit.为了将数据传输的更远，放大电路功耗为100 pJ/bit·m2，通信距离为50 m，仿真时间为1 000 s，数据大小为512 byte，无线传感器网络的协议为802.15.4。离群时间序列检测算法的精确度如公式所示。

3.1 切比雪夫系数的选取

传感器节点采集的数据以20 s为一个基本窗口，离群时间序列的速度为每100 s出现一次。对时间序列进行切比雪夫转化，分别取系数的值为[0，25]中的整数.基于文献[13]Yongzhen Zhuang等人提出了基于无线传感器网络中离散小波变换(DWT)离群数据检测，图2显示了DWT算法与本文的FODA算法中切比雪夫系数选取的比较。切比雪夫系数与小波变换系数类似，取系数值在4到8之间时，检测精确度在90%以上，取5左右时精确度最好。

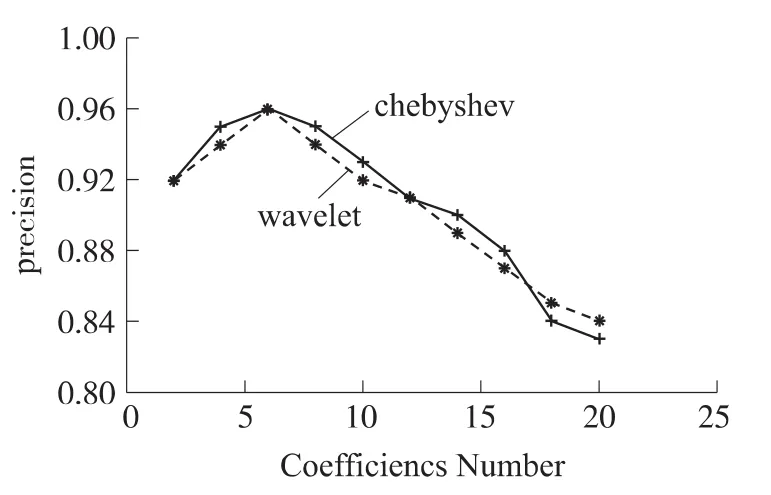
图2 切比雪夫和小波变换系数的选取比较

3.2 精确度比较

传感器节点采集的数据以20 s为一个基本窗口，离群时间序列的速度分别为每100 s，200 s，300 s，400 s，500 s各一个。对这5组数据进行离群时间序列检测。

(1)传感器节点采集的数据维度d=1。由文献[16]可以得知，利用PAA和切比雪夫思想进行时间序列相似性判定时，切比雪夫思想比PAA更好。图3显示了PAA的离群时间序列检测与FODA算法检测在一维数据上的精确度比较，实验证明在一维数据上，FODA算法比PAA的离群时间序列检测精度稍高。本文利用切比雪夫多项式进行无线传感器网络环境中的离群数据检测，目前，尚未见类似的工作。

图3 一维时间序列数据，PAA算法与FODA算法精度比较

(2)传感器节点采集的数据维度d=4时。图4显示了PAA的离群时间序列检测与FODA算法检测在4维数据上的精确度比较。同上述一样，实验证明在多维数据上，FODA算法比PAA算法的离群时间序列的检测精确度较高。

图4 多维时间序列数据，PAA算法与FODA算法精度比较

3.3 CPU速度比较

传感器节点采集的数据维度d=1。比较了FODA算法和PAA算法的时间效率。由图5可以看出，FODA算法所消耗的CPU时间低于PAA的离群时间序列检测所消耗的CPU时间。

图5 一维时间序列数据，PAA算法与FODA算法速度比较

取传感器节点采集的数据维度d=4，对FODA算法和PAA算法的时间效率进行了仿真。如图6所示，FODA算法所消耗的CPU时间也低于PAA的离群时间序列检测所消耗的CPU时间。

图6 多维时间序列数据，PAA算法与FODA算法速度比较

从上述两组仿真实验可以看出，FODA算法在速度方面优于PAA算法。主要原因是:PAA算法的时间复杂度是O(N)，其中N为时间序列的长度。而FODA算法的时间复杂度是O(n)，其中，n为切比雪夫系数个数，而n远远小于N，因此FODA算法执行速度明显快于PAA的离群时间序列检测算法。

4 总结与展望

本文提出的无线传感器网络离群时间序列检测算法，不仅适用于低维的离群时间序列数据检测，而且适用于高维的离群时间序列数据检测，同时保持了较高的检测精度。本文利用切比雪夫多项式系数判定两个时间序列的相似度能够快速的检测离群时间序列。通过实验验证了上述结论。接下来的工作是为了节省网络能量消耗，我们考虑无线传感器网络分簇的问题并将提出的算法与实际应用结合起来。

[1]任丰原，黄海宁.无线传感器网络[J].软件学报，2003，14(7):1282－1291.

[2]周贤伟，王培，覃伯平，等.一种无线传感器网络异常检测技术研究[J].传感技术学报，2007，20(8):1870－1874.

[3]杨黎斌，慕德俊，蔡晓妍.基于核聚类的无线传感器网络异常检测方案[J].传感技术学报，2008，21(8):1442－1447.

[4]孙金花，胡建.基于分型理论的离群点检测[J].计算机工程，2011，37(3):33－35.

[5]Vu N H，Gopalkrishnan V.Efficient Pruning Schemes for Distance-Based Outlier Detection[C].Proc.of the European Conference on Machine Learning and Knowledge Discovery in Databases，2009:160－175.

[6]薛安荣，鞠时光，何伟华，等.局部离群点挖掘算法研究[J].计算机学报，2007，30(8):1455－1463.

[7]Faloutsos C，Ranganathan M，Manolopoulos Y.Fast Subsequence Matching in Time-Series Databases[C].Proc.SIGMOD，1994:419－429.

[8]Wu Y，Agrawal D，Abbadi A.A Comparison of DFT and DWT Based Similarity Search in Time-Series Databases[C].Proc.CIKM，2000:488－495.

[9]Keogh E，Chakrabarti K，Pazzani M，et al.Locally Adaptive Dimensionality Reduction for Indexing Large Time Series Databases[C].Proc.ACM SIGMOD，2001:151 –162.

[10]Keogh E，Chakrabarti K，Pazzani M，et al.Dimensionality Reduction for Fast Similarity Search in Large Time Series Databases[J].Journal of Knowledge and Information Systems，2000:263－286.

[11]Yang Zhang，Nirvana Meratnia，Paul Havinga.Outlier Detection Techniques for Wireless Sensor Networks:A Survey[J].IEEE Communications Surveys ＆ Tutorials，2010，12(2):1－12.

[12]Dang-Hoan Tran，Jin Yang.Decentralized Change Detection in Wireless Sensor Network Using DFT-Based Synopsis[C].The 12thIEEE International Conference，2011:226－235.

[13]Zhuang Yongzhen，Chen Lei.In-Network Outlier Cleaning for Data Collection in Sensor Networks[C].Proceedings of Very Large Data Bases，2006.

[14]Sheng Bo，Li Qun，Mao Weizhen.Outlier Detection in Sensor Networks[C].Proc of the 8th ACM International Symposium on Mobile Ad hoc Networking and Computing.New York:ACM Press，2007:219－228.

[15]Kifer D，Ben-David S，Gehrke J.Detecting Change in Data Streams[C].In Proceedings of the Thirtieth International Conference，2004:180－191.

[16]Cai Yuhan，Raymond Ng.Indexing Spatio-Temporal Trajectories with Chebyshev Polynomials[C].Proc.ACM SIGMOD，2004:599－610.

[17]Mason J C，Handscomb D C.Chebyshev Polynomials[M].Chapman and Hall/CRC，2011，9.