电阻式压力敏感阵列足底压力测量及噪声滤除方法研究*

蔡 楷，毛志勇，蔡 萍

(上海交通大学仪器工程系，上海200240)

人体足底压力分布测量广泛应用于糖尿病等的疾病分期、康复救治、体育训练及特殊功能鞋的设计等方面。压力分布测量的传感器阵列通常有电阻式、电容式及压电薄膜式等。电容式敏感阵列制作成本高、测量电路复杂;压电传感器存在分辨率和精度都较低的问题[1]。利用电阻油墨制成的压阻式压力敏感阵列因具有制作工艺简单、易于实现大规模阵列、与前两者相比抗干扰能力较强等优点而得到广泛应用。

电容式、压电式和电阻式压敏单元三者的敏感机理虽各不相同，但内阻都很高，对外界电气干扰十分敏感。此外，行列扫描时，模拟开关高速切换引起的开关噪声也会严重污染压力云图数据结果。为此，对压力云图数据进行恰当的空域滤波，是压力分布测量中有待解决的共性技术。中值滤波是图像处理中一种经典的噪声滤除方法，该方法对窗口内的像素按照灰度值排序，取其中值作为窗口中心像素的滤波输出，能够有效滤除脉冲噪声。在此基础上发展出的中心加权中值滤波[2]、开关中值滤波[3]、窗口自适应中值滤波[4]和 IMF 中值[5](Improved Median Filter)等从不同角度对标准中值滤波进行了改进。中心加权中值滤波对中心元素进行加权复制后进行中值滤波;开关中值滤波对当前窗口内的噪声水平进行判定后使用不同的滤波方法;窗口自适应中值滤波则在判断当前窗口无法滤除噪声时，自适应扩大滤波窗口的大小，从而获得更加准确的滤波效果;IMF算法结合了中值滤波和均值滤波[6]特性，既能抑制脉冲噪声也能抑制高斯噪声。但是以上这些滤波方法对本系统的噪声滤波效果不佳，故而本文在分析IMF算法特点的基础上，借鉴开关滤波的思路，提出了一种改进的IMF中值滤波方法，实验结果表明，改进的IMF中值滤波方法较IMF等其它滤波方法具有更好的去除噪声能力。

1 压力分布测量系统简介

系统构成如图1(a)所示，主要包括压力敏感阵列、行列扫描电路和零电势放大电路和模数转换等四部分。电阻敏感阵列如图1(b)所示，其由上、下两张印刷有电阻油墨图案的塑料薄膜相向叠合而成。电阻油墨的印刷图案为一组平行线，上、下两张薄膜的平行线正交交叉相触形成触点阵列，交叉点即为压阻敏感单元。敏感单元处的压力大小通过该敏感单元的阻值反映，电阻值与压力成反比，压敏特性如图1(c)所示。

以行列形式连接的敏感阵列其选通单元和其余非选通单元之间存在复杂的串并联关系，串扰是首要解决的问题。图1(d)为4×4的敏感单元阵列示意图，图中R22为选通单元，可以看到，非选通的其它单元以组合并串的方式形成R22的旁路，引起串扰。但只要将非选通行全部接地，即所谓零电势电路，其等效电路如图1(e)所示，旁路电阻串完全不影响通过R22的电流，有效抑制了串扰。系统选用超高速模数转换电路AD9012，其转换速度达100 MSPS，以满足动态压力分布测量的要求。

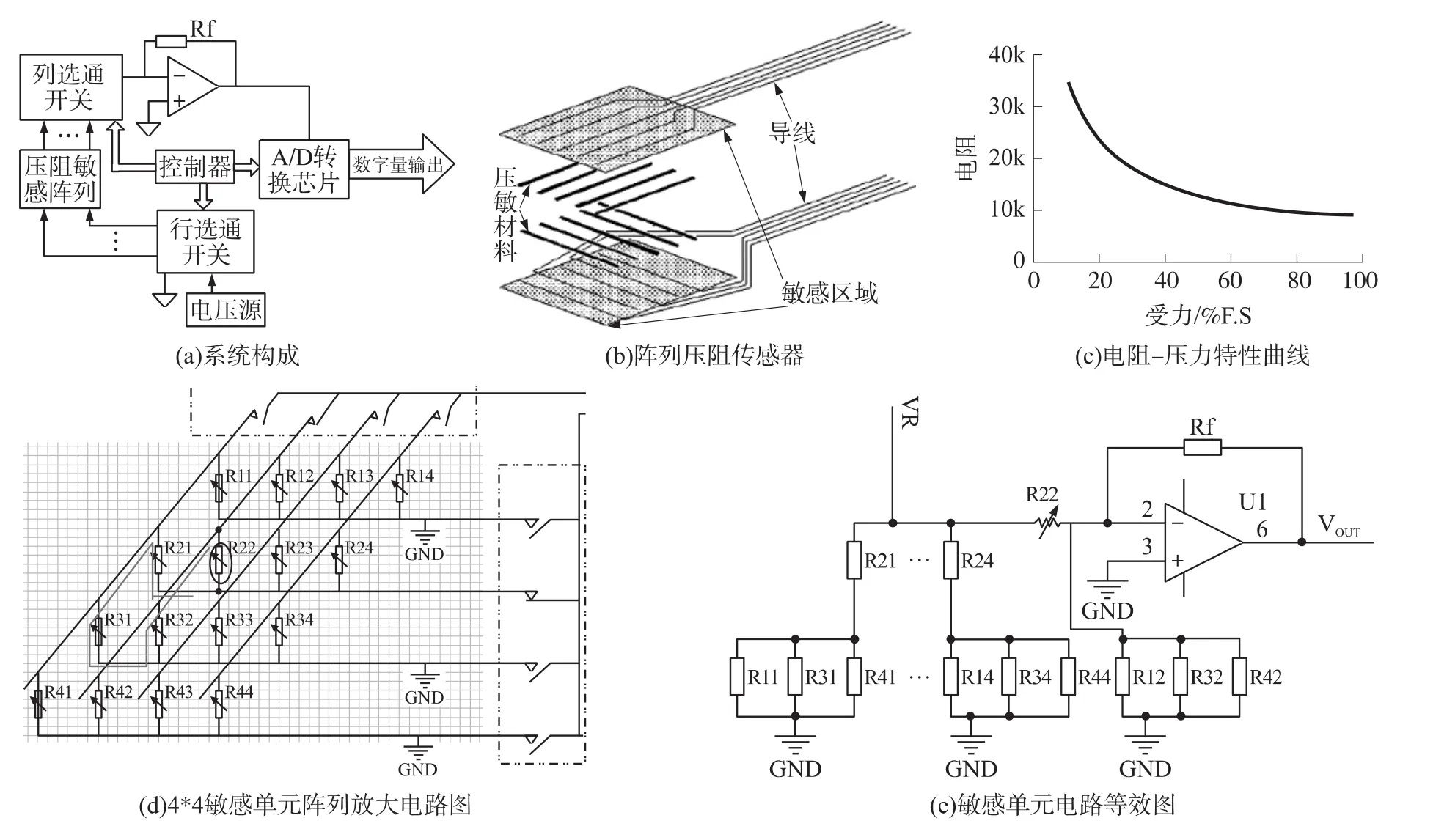
图1 压力分布测量系统

2 系统噪声及IMF滤波方法分析

压力分布测量通过行选通和列选通模拟开关将敏感单元逐一接入电路获得测量结果，由于各模拟开关的响应特性存在差异，在高速切换过程中会出现短时无敏感单元接入的情况，此时高速A/DC对放大电路的饱和输出进行转换，由此引入脉冲噪声。这一噪声对足底压力云图的影响非常显著，在数据插值后将造成较大的噪声输出，故而需要专门针对这一噪声设计滤波算法。

此外，高速A/D固有的对电气干扰的敏感、电阻油墨材料电导率不均匀导致的噪声、和A/D的量化误差[7]等引起的信号波动表现为高斯噪声的特点。

IMF算法在简单中值滤波的基础上，将滤波窗口内的其它像素进行求权相加，具有同时滤除脉冲噪声和高斯噪声的能力。考虑像素点g(x，y)，滤波窗口win(x，y)，对其进行中值滤波，获得灰度中值M(x，y)，由此求得滤波窗口各像素点g(m，n)和灰度中值的方差:

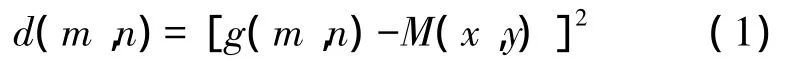
像素点对应的权值为:

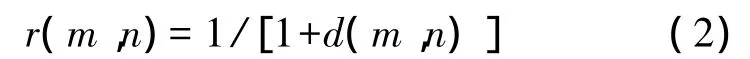
其归一化权值为:

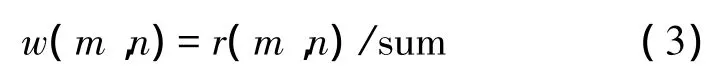
则该像素点的滤波输出为

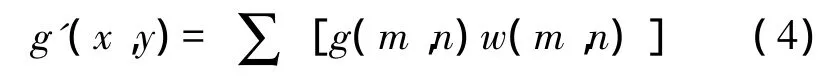
该算法使用窗口内的各个像素与滤波窗口中值的方差计算获得权值，通过使用中值抑制脉冲噪声，通过窗体内像素的加权求和抑制高斯噪声。这一算法没有对各个像素点上的噪声性质进行甄别，对各个像素使用了同样的滤波方法，缺乏针对性。由式(2)和式(4)可知，当窗口内某个点的灰度值同中值非常接近时，该点会获得相当大的权值，此时的滤波算法接近于简单的中值滤波，故有必要对这一方法进行改进。

3 自适应中值滤波方法及实现

借鉴开关中值滤波的思想[8]，使用模板对窗口中心点是否为脉冲噪声进行判断，若为脉冲噪声，对当前的窗口使用中值滤波进行滤除;对上一步处理后窗口数据，使用改进的IMF滤波算法。具体的算法步骤如下。

(1)使用边界模版

压力分布正常数据的灰度值达到极值的像素点相对集中，具有连续性，并具有连续性的边界，这一特点可用于准确鉴别是正常的局部压力集中还是脉冲噪声。本算法参考方向卷积模板[9－10]，使用边界模板进行脉冲噪声的检测。记3×3滤波窗口(中心元素坐标为(x，y)，记窗口为 win(x，y))，当中心像素的灰度值为灰度极值时，使用四种方向上的模板[11]，如图2 所示。

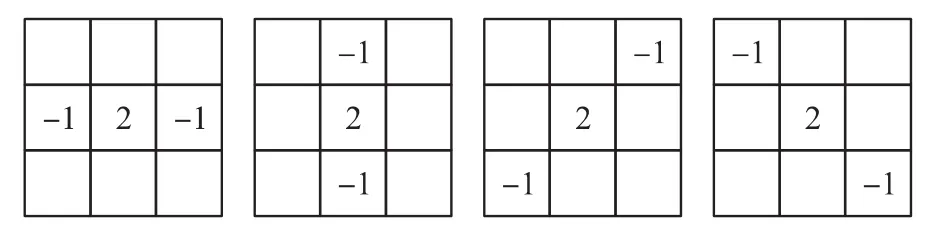
图2 四种方向的边界模板

按照边界模版中的权值，对滤波窗口的数据做累加计算，获得四个方向上的灰度差值。由于正常压力分布其灰度极值的出现是连续的，并且在连续区域的外部具有连续的边界，基本边界方向同图2所示模板相似，在这四个方向上的差值应当在一定的范围内，该值可通过实验获得，在本系统采集到的压力分布图像中，像素灰度为0～255，则差值一般在0～50之间，在此将50设定为阈值，记为Ttemplate，当四个方向上的灰度差值均大于Ttemplate时，即可判断该点为脉冲噪声，并将其滤除。

(2)拓展时间窗口

在图像的3×3滤波窗口之外，在时间序列上拓展窗口[12]，使用前2帧图像滤波后的结果以及当前采集的图像，将这三帧图像的窗口叠加，拓展成3×3×3的窗口，并对当前采集图像的窗口的中心元素进行加权，增强中心元素的作用，求出该窗口的均值 M(x，y)3×3×3。而后使用式 (1)获得各个像素点 g(m，n)的灰度方差 d(m，n)3×3×3。

(3)阈值自适应权值及滤波算法实现

针对IMF算法的缺点，对式(2)进行改进，设定一个自适应阈值T[13]，当灰度方差大于T时，使用式(1)计算获得的灰度方差进行权值计算;而当灰度方差小于T时，使用T代替原有方差进行权值计算。当阈值T取得较大时，这一算法接近于典型的均值滤波，本文取阈值为

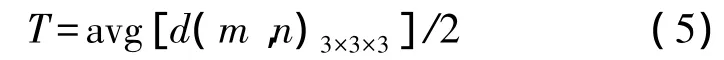
avg为对窗口内的数值做平均。则式(4)变形为

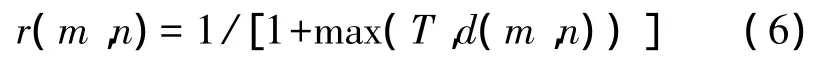
而后根据式(5)、式(6)计算获得最后的滤波输出。本算法中，阈值T的大小由窗口内部的数据自适应调整，规避了固定的阈值会导致的性能问题。算法流程如图3所示。

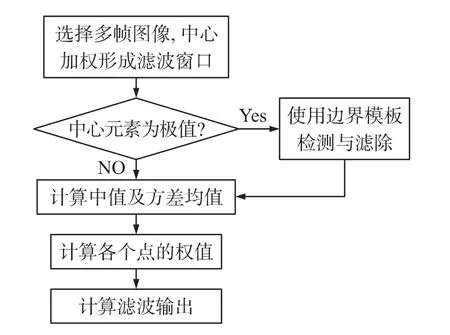
图3 滤波算法流程

4 实验验证与算法性能比较

为了评价算法滤除噪声的能力，引入信噪比改善因子[14]R(db):

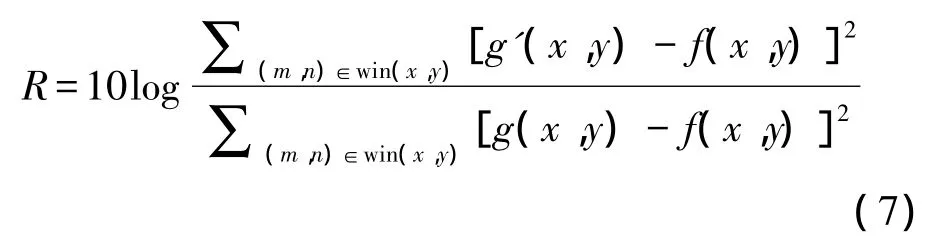
其中，g'(x，y)为滤波后的输出图像，f(x，y)是不带噪声的标准图像，g(x，y)是加有噪声图像。由定义式(7)可知，当R(db)为负值时，说明滤波后噪声被抑制，R(db)越低，滤波算法效果越好。

标准图像如图4(a)所示。在滤波过程中使用灰度进行计算，最后进行颜色映射形成压力云图显示。在图中加入空间密度为0.01的脉冲噪声和均值为 0，方差为 0.01的高斯噪声，噪声图像如图4(c)所示。

图4

图5 颜色映射对照表

使用IMF滤波算法和本文提出的阈值自适应调整的中值滤波算法对图像进行滤波的结果如图6(a)和6(b)所示，可见本文提出的滤波方法在足底分布云图的应用中具有更好的滤波能力。

图6 IMF滤波算法和阈值自适应改进中值滤波算法

对图4(a)所示图像分别加入方差为 0.03、0.01、0.005 的高斯噪声及空间密度为 0.01 的脉冲噪声，分别使用以上两种算法进行滤波后计算R(db)。两种算法的性能比较如表1所示。可以看出，本文提出的算法具有更好的信噪比改善因子。

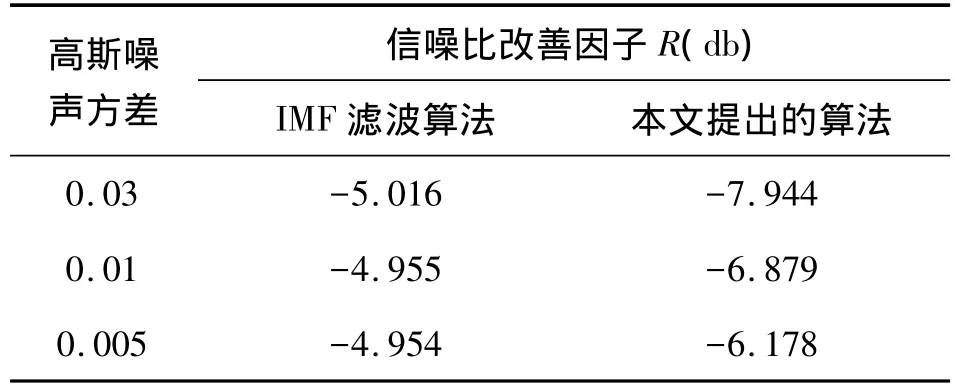
表1 不同方差下信噪比改善因子

对图6(b)所示结果进行零位补偿后得到图7。从图中可以看出足底压力云图的边界同参考标准图像非常接近，基本达到了实际应用的要求。

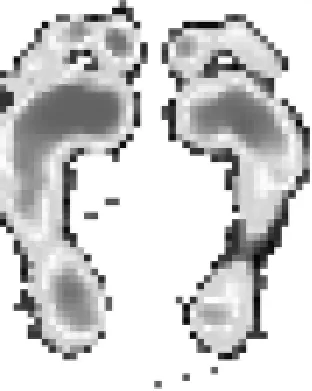
图7 减去敏感单元零位输出后的图像

5 结语

本文介绍了一种足底压力分布测量系统，讨论了系统噪声的来源，并对这一系列噪声进行滤波。在本文提出的方法中，先使用模板对图像灰度极值的像素点进行鉴别，判断是否为脉冲噪声，而后根据多帧图像之间的连续性，拓展普通的滤波窗口为时间先后范畴上的时间窗口，使用前次采集获得的滤波图像帮助甄别当前滤波图像中的噪声，并通过阈值自适应的加权中值滤波算法进行噪声滤除，实验结果证明这一算法相对于IMF等滤波方法具有更强的噪声抑制能力。在系统实际应用中，提出去除阵列单元零位输出的策略，这一策略在恢复图像的边界上具有一定的意义。

[1]庄燕子，蔡萍，周志锋，等.人体压力分布测量及其传感技术[J].传感技术学报，2005，18(2):313－317.

[2]梁雯，刘松林.图象中心加权中值滤波的改进与应用[J].中国图象图形学报，1997，2(8):629－632.

[3]Kenny Kal Vin Toh，Nor Ashidi Mat Isa.Noise Adaptive Fuzzy Switching Median Filter for Salt-and-Pepper Noise Reduction[J].IEEE Signal Processing Letters，2010，17(3):281－284.

[4]张旭明，徐滨士，董世运.用于图像处理的自适应中值滤波[J].计算机辅助设计与图形学学报，2005，17(2):295－299.

[5]张恒，雷志辉，丁晓华.一种改进的中值滤波算法[J].中国图象图形学报，2004，9(4):408－411.

[6]卢京晶，方中华，孙胜利.一种自适应的加权均值滤波器[J].传感技术学报，2005，18(4):880－882.

[7]曾庆勇.微弱信号检测[M].浙江大学出版社，1986.

[8]于忠党，王龙山.基于回归型最小二乘支持向量机卷积模板的椒盐噪声开关滤波器[J].光学学报，2009，29(1):163－168.

[9]Xu Haixiang，Zhu Guangxi，Peng Haoyu，et al.Adaptive Fuzzy Wwitching Filter for Images Corrupted by Impulse Noise[J].Pattern Recognition Letters，2004，25(15):1657－1663.

[10]李彦军，苏红旗，杨峰.改进的中值滤波图像去噪方法研究[J].计算机工程与设计，2009，30(12):2995－2997.

[11]王建勇，周晓光，廖启征.一种基于中值模糊技术的混合噪声滤波器[J].电子与信息学报，2006，28(5):901－903.

[12]谢勤岚.结合双边滤波和多帧均值滤波的图像降噪[J].计算机工程与应用，2009，45(27):154－156.

[13]常瑞娜，穆晓敏，杨守义，等.基于中值的自适应均值滤波算法[J].计算机工程与设计，2008，29(16):4257－4259.

[14]武英，吴海勇.一种自适应图像去噪混合滤波方法[J].计算机工程与应用，2010，46(7):168－170.