0-1线性规划的连续化求解方法

刘山，张林玲，郝立东，曹盛文

（中国民航大学计算机科学与技术学院，天津300300）

0-1线性规划的连续化求解方法

刘山，张林玲，郝立东，曹盛文

（中国民航大学计算机科学与技术学院，天津300300）

针对0-1线性规划的优化问题，提出一种惩罚函数方法。考虑到0-1线性规划的最优值特征，通过在目标函数中加上惩罚函数，将0-1离散线性规划模型连续化成非线性规划模型，并使用Matlab的Fmincon函数进行求解。经对多个算例的计算，并和其他算法比较，结果表明惩罚函数法的可行性和有效性。将该方法应用于实际的飞机排班问题上，取得比较满意的结果。

0-1线性规划；惩罚函数法；连续化

0-1线性规划是整数规划的一种特殊形式，是运筹学中一个典型的组合优化难题。0-1线性规划在飞机排班、厂址选择、人员安排、项目评价、资金分配等方面有着广泛的应用。研究0-1线性规划问题的求解方法具有很重要的理论意义和实用价值。

目前求解0-1线性规划问题的方法主要有分枝定界法、完全枚举法、启发式算法和连续化方法等。前两种方法实质是组合优化方法，穷举所有的可行解并选择其中的最优解，这类方法随着问题规模的扩大计算代价会增加，当问题规模很大时，可能出现无法求解的情况。启发式算法是建立符合实际问题的启发式规则的搜索算法，如用0，1编码表示的遗传算法[1]，但是遗传算法在如何处理约束的问题上存在困难，大多数遗传算法只是针对某一类问题的改进，没有通用和完善的计算机程序。连续化方法是将原问题转化为关于连续变量的规划问题后求解。0-1离散模型属于组合优化问题，当问题规模很大时，面临组合爆炸的难题，连续化方法可以避开组合优化的问题，不受求解问题规模大小的限制。隋允康[2]等人将0-1离散规划通过一个非线性等式约束表示为[0，1]区间上等价的连续变量非线性规划列式，使用乘子法、离散约束变换法处理后利用遗传算法GENOCOP进行求解。但是没有考虑目标函数中变量的系数对目标函数值的影响，在有些情况下并不能有效的求得0，1最优解或近似最优解。李兴斯[3]等人利用互补约束代替0-1条件，并利用凝聚函数法进行光滑处理来求解0-1线性规划问题。但是该方法只适用于某一类0-1线性规划问题，应用上有局限性。

本文首先将0-1线性规划问题表示成一个[0，1]区间上的连续变量的非线性规划问题，在目标函数中设计一个具有大M法功能的惩罚函数，将变量驱赶到使模型取得最优值的0或1。然后采用Matlab的Fmincon函数求解模型的最优解，最后对该规划问题求得的小数解，根据修正策略进行合理的修正，最终得到原规划问题的0，1最优解或近似最优解。

1 问题的提出

对于0-1线性规划问题P

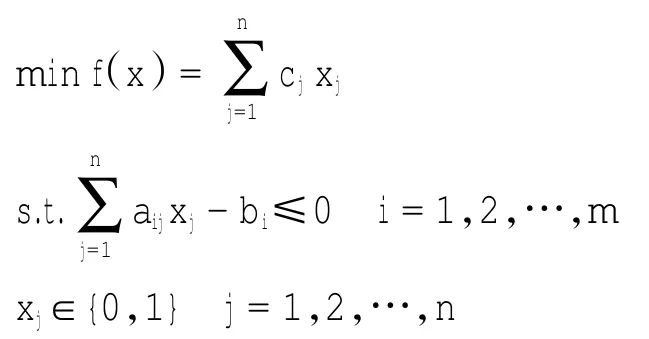
一般连续化方法的做法是在目标函数中加上一个关于对变量约束的函数，转化为如下规划问题P1

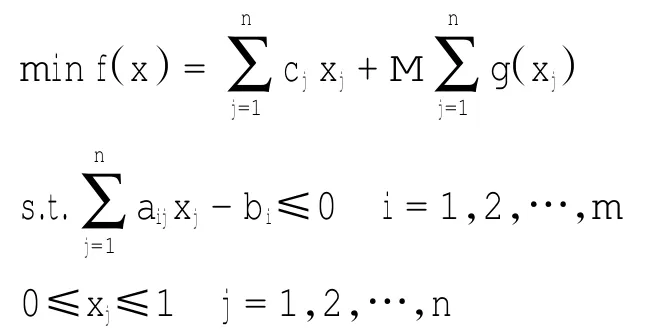
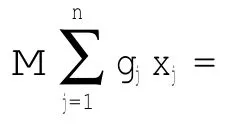
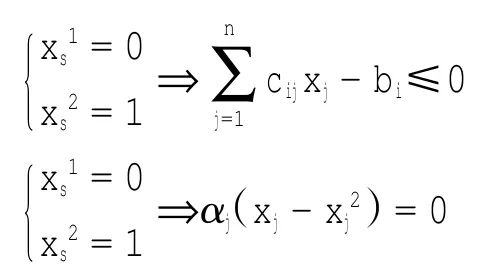
此时目标函数f（xs1）＞f（xs2），显然，当xs取1时，目标函数值最优，而乘子法在处理这类规划问题时不能准确地判断变量的取值对目标函数值的影响。基于乘子法的不足，本文提出一种惩罚函数法。

2 惩罚函数法

2.1 惩罚函数法的思想及连续化

惩罚函数法首先将0-1离散模型表示成连续变量的非线性规划模型，然后求解该模型找到满足约束、使目标函数值最优的0，1最优解或近似最优解。惩罚函数法的基本思想：当求解目标函数最小值时，在满足约束的条件下，使用具有大M法功能的函数将对应大于0的目标函数系数的变量驱赶到0，对应小于0的目标函数系数的变量驱赶到1。利用这个思想，在原目标函数中加上一个惩罚函数，进而得到一个增广的目标函数，通过该惩罚函数值的变化控制变量的取值趋势。

对于上述0-1线性规划问题P，在目标函数中加上惩罚函数得到如下连续的非线性规划问题

2.2 惩罚函数的构成

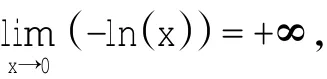
图1 –ln（x）和sin（x）的图像Fig.1Image of–ln（x）and sin（x）

3 连续化0 -1 非线性规划问题的求解

3.1 求解原理

本文采用Matlab的Fmincon函数求解连续化后的0-1非线性规划问题。函数的主要输入参数有目标函数表达式、初始值、约束矩阵等，主要输出有规划问题的最优解、目标函数的最优值和每次迭代过程的优化信息等。对于不包含梯度信息的非线性规划问题，Fmincon主要运用了序列二次规划算法、拟牛顿法和线性搜索法的结合求解问题。序列二次规划算法是将求解非线性约束优化问题转化成求解一系列二次规划子问题来实现。在一次次迭代中，产生可行解的一个迭代序列，这个序列收敛得到问题的解。设xk是当前问题的迭代点，则求搜索方向d的二次规划子问题的目标函数为

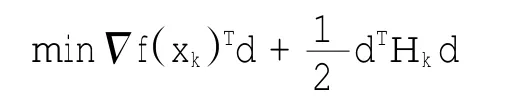
3.2 解的修正策略

在求解某些规划问题时，可能出现小数解，需要修正。假设求得的解中变量xj为小数，判断xj系数cj是否大于0，分为两种情况：①当cj>0时，根据以上分析，要使惩罚函数中F2=0，则因为0≤xj≤1，显然，xj =0不能满足约束条件。因此将xj修正为1。②当cj＜0时，同理，xj=1使惩罚函数中F1=0。因为0≤xj≤1，显然，xj=1不能满足约束条件。因此将xj修正为0。

4 算例分析

为了验证本文提出方法的有效性，运用惩罚函数法、乘子法和分枝定界法求解以下算例。其中乘子法为文献[2]中的方法。分枝定界法采用Matlab的bintprog函数求解，函数的主要输入和输出与Fmincon函数类似。

4.1 算例1

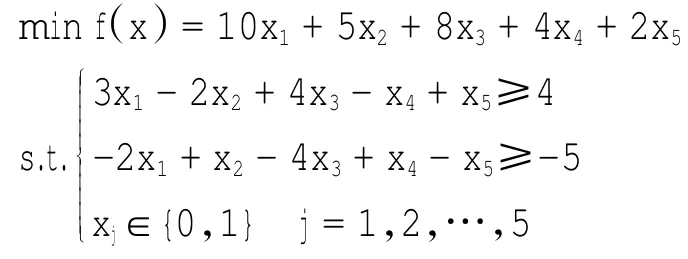
算例1的计算结果如表1所示。

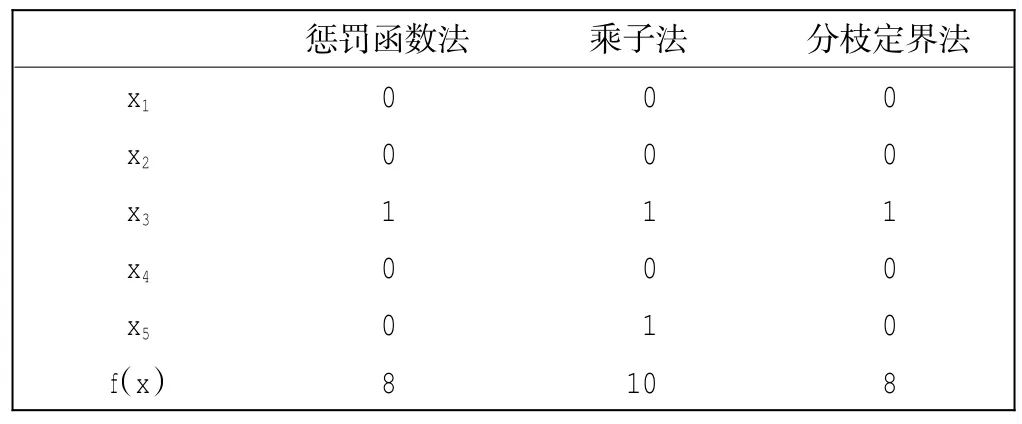
表1 算例1的计算结果Tab.1Result of example 1

4.2 算例2

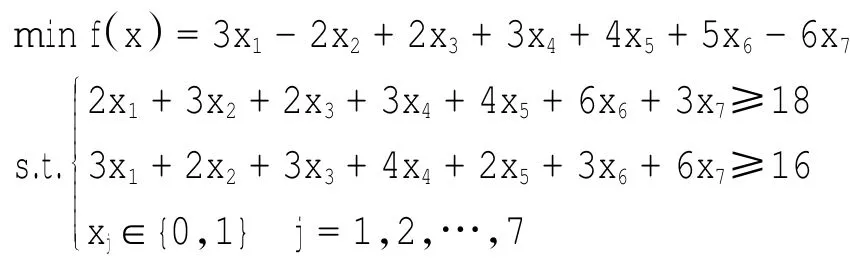
惩罚函数方法求解得（0.000 0，1.000 0，0.000 0，0.800 0，0.900 0，1.000 0，1.000 0），经过修正策略得（0，1，0，1，1，1，1）。

算例2的计算结果如表2所示。

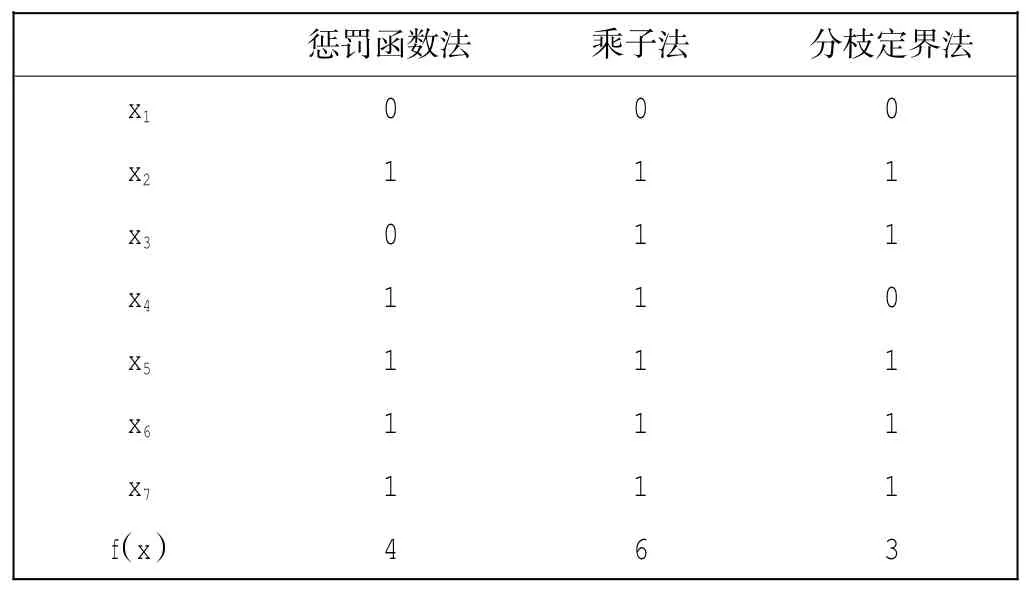
表2 算例2的计算结果Tab.2Result of example 2

4.3 算例3

算例3的计算结果如表3所示。

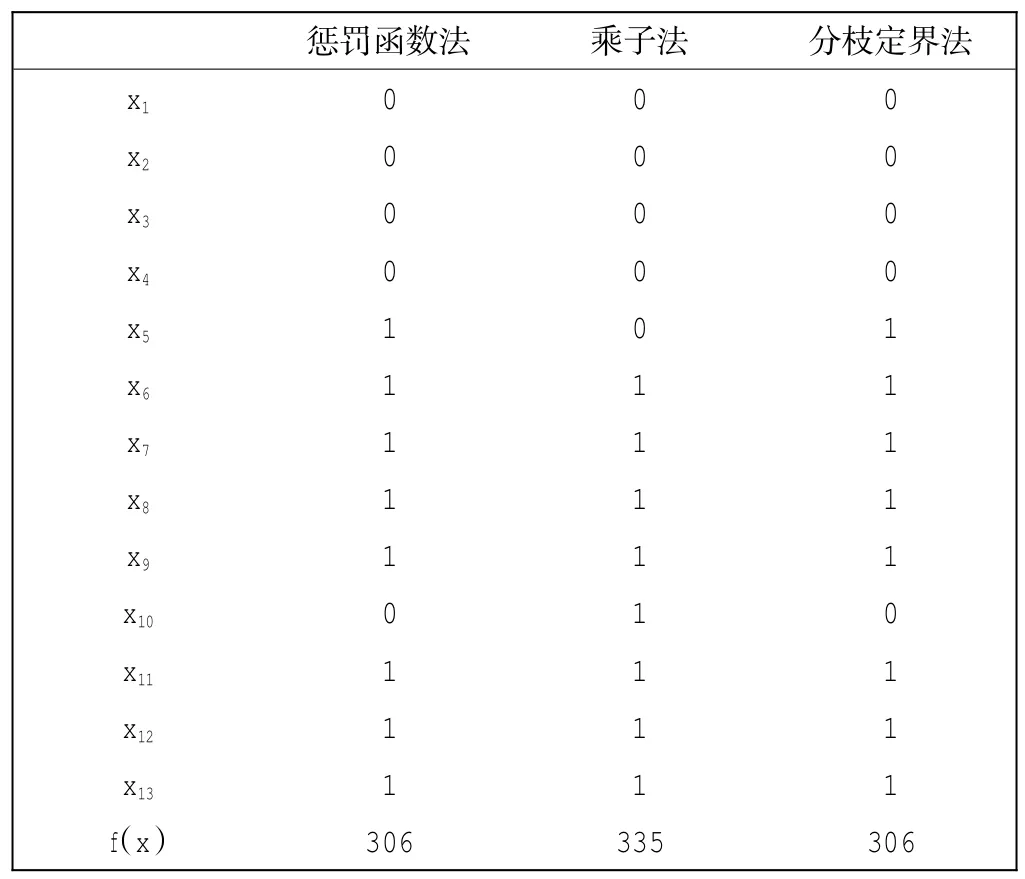
表3 算例3的计算结果Tab.3Result of example 3

算例1中目标函数的系数为正，由计算结果看到，惩罚函数法和分枝定界计算结果相同，略优于乘子法。算例2和算例3中目标函数的系数为负，计算结果表明，随着变量个数的增多，惩罚函数的效果明显比乘子法好。从整体上看，无论变量个数多少，目标函数中变量系数的正负个数多少，惩罚函数法在求解0-1线性规划问题上具有一定的优势。

5 惩罚函数法在飞机排班问题上的应用

飞机排班是指为每个航班指定一架具体执行的飞机。航班衔接条件[4]是指：①相邻航班的机场、时间约束，即前一航班的到达机场和后一航班的出发机场必须相同，且有一定的时间间隔；②相邻的两个航班的前一个航班的到达时间和后一个航班的出发时间如果不在同一天，应确定两航班是否能够过夜。航班环[5]是指由一架飞机连续执行的飞机路线，即一组满足航班衔接条件的航班组合，且首个航班的出发机场和终止航班的到达机场为维修基地。目前国内飞机排班的流程分为两步，第一步构建航班环，第二步筛选航班环，为每架飞机安排实际运营路线。构建航班环的主要方法有列生成法[5]、深度优先搜索算法[6]等。

本文选取国内某航空公司A320飞机一周执行的航班，共100个，飞机共8架。考虑一种机型的飞机分配问题。首先通过深度优先搜索生成所有可行的一天航班环和任意相邻的两天航班环，共245个。其次考虑航班计划、飞机数量限制等因素，建立筛选模型

式（1）中xj表示第j个航班环，即目标函数是保证航班环的个数最少；约束条件（2）是航班覆盖约束，即每个航班只能被一个航班环覆盖，共有100个约束条件；约束条件（3）是飞机数量的约束，即执行每天的航班环所需的飞机架数不能超过此机型当天可用的飞机数量，Pw表示第w天的可用飞机数量，共有7个约束条件。

筛选航班环的目的是确定一个航班环是否被选择，被选择为1，不被选择为0，实质是0-1规划问题。上述模型有变量245个，等式约束100个，不等式约束7个，属于大规模0-1线性规划问题，随着航班量的增多，计算量呈指数增长，求解难度加大。目前求解航班环筛选模型的算法有单纯形法[4]、遗传算法[5]等。使用遗传算法时，由于等式约束的存在，在遗传过程中不利于新个体的产生。单纯形法对于解决大型规模的规划问题并没有很好的效果。使用本文提出的方法对0-1筛选离散模型连续化得

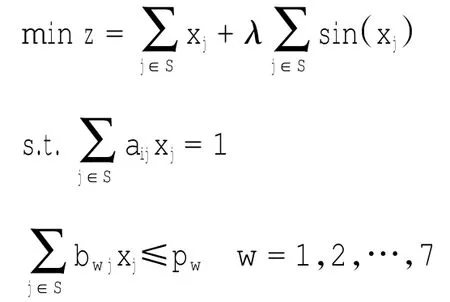
xj∈{0，1}j=1，2，…，245

利用Matlab的Fmincon函数求解0-1非线性连续化模型。其中每个航班环是连续化模型中的一个变量。求解得满足约束的最少航班环的个数为28个，即在245个变量中，28个变量的值为1，其余变量的值为0。筛选出的航班环能够覆盖一周所有航班且每个航班只被覆盖一次。航班环的筛选结果如表4所示。

表4 航班环筛选结果Tab.4Result of optimization of flight-loop

6 结语

本文通过在目标函数中增加一个惩罚函数的方法，将原0-1线性规划问题转化为[0，1]区间上的连续变量非线性规划问题，并利用Matlab的Fmincon函数求解，对有些规划问题求得的小数解进行合理的修正，最终得到满足约束的0，1最优解或近似最优解。经过多个算例的测试，结果表明该方法的可行性和有效性。通过将惩罚函数法用于飞机排班问题上，并取得比较满意的结果，表明该方法可以应用于实际中0-1线性规划问题的计算。本文提出的方法不是局限于某一类0-1线性规划问题，该方法的特点是对原目标规划处理简单，不需要复杂的特殊处理，求得的结果稳定、有效，为求解大型规模的0-1线性规划问题开拓一种新思路。根据惩罚函数法的思想可以将该方法应用于求解0-1非线性整数规划和0-1非线性混合整数规划。由于本文的方法中惩罚函数是由ln（x）函数和sin（x）函数的组合构成的，根据相关的数学知识推出，ln（1-x）的斜率比sin（x）的斜率大，更有利于惩罚函数有效判断变量的取值趋势，但是通过计算实际的算例，表明ln（1-x）并没有sin（x）效果好，这也是下一步思考和研究的重点。

[1]李晓萌，戴光明，石红玉.解决多维0/1背包问题的遗传算法综述[J].电脑开发与应用，2006，19（1）：4-5.

[2]隋允康，贾志超.0-1线性规划的连续化及其遗传算法解法[J].数学的实践与认识，2010，40（6）：119-127.

[3]李兴斯，谭涛.求解二进制二次规划问题的一种连续化方法[J].工程数学学报，2006，23（3）：500-504.

[4]沈中林，李延朵.遗传算法在航班覆盖问题中的应用研究[J].中国民航大学学报，2008，26（6）：5-9.

[5]肖东喜，朱金福.飞机排班中航班环的动态构建方法[J].系统工程，2007，25（11）：19-25.

[6]付维方，张伟刚，孙春林.航班排班中航班串生成与筛选问题的算法与实现[J].中国民航学院学报，2006，24（5）：4-6.

（责任编辑：杨媛媛）

Continuous method for solving 0-1 linear programming

LIU Shan，ZHANG Lin-ling，HAO Li-dong，CAO Sheng-wen
（College of Computer Science and Technology，CAUC，Tianjin 300300，China）

To optimize the 0-1 linear programming，a method of penalty function is proposed.According to the features of the 0-1 linear programming optimal value，the penalty function is added with the target function and the 0-1 discrete model is changed into the continuous model which is nonlinear equally.The nonlinear model is solved by Fmincon function of Matlab.The results with example calculation and comparison with other algorithms show that this method is feasible and effective.This method is applied to the actual aircraft scheduling and the result is satisfying.

0-1 linear programming；a method of penalty function；continuous

F560

A

1674-5590（2013）03-0045-05

2012-06-15；

2012-09-06

国际合作与交流专项基金（2008DFA12300）

刘山（1955—），男，天津人，教授，学士，研究方向为数据挖掘、计算机视频.