基于QAR的飞机爬升阶段燃油流量回归模型研究

曹惠玲，贾超

（中国民航大学航空工程学院，天津300300）

基于QAR的飞机爬升阶段燃油流量回归模型研究

曹惠玲，贾超

（中国民航大学航空工程学院，天津300300）

以B777-200飞机选装的PW4077D发动机为研究对象，对QAR数据进行深入分析，运用多元回归分析的方法，建立飞机爬升阶段发动机燃油流量回归模型，并通过实际数据对模型进行准确性验证，研究结果为发动机燃油控制规律的全面研究奠定一定的基础，可实现对发动机燃油流量的监控与预测，提高飞机的安全性和经济性。

航空发动机；燃油流量；回归模型；QAR

QAR（quick access recorder）数据是飞机飞行品质和发动机状态监控的重要数据来源，这些数据可以反映参数之间的相互关系，也蕴含着某种控制规律[1-2]，因此可以通过对其进行深入分析，研究发动机的性能变化及控制规律。燃油流量作为飞机安全性和经济性的重要指标，一直是研究人员和航空公司比较关心的一个重要指标，飞机在爬升阶段，飞行状况是最复杂的，燃油调节规律随之复杂，发动机性能衰退趋势在这个阶段也最明显。研究并建立飞机爬升阶段发动机燃油流量调节规律数学模型，通过模型监控其异常变化，以提高飞机的安全性和经济性。

本文以B777-200飞机选装的PW4077D型发动机25个航班的QAR数据为研究对象，选用多元统计分析中的逐步回归分析法进行统计和分析，旨在建立飞机爬升阶段发动机燃油流量回归模型并验证其准确性。

1 多元线性回归模型

建立“最优”回归方程有多种方法，目前常用的有“前进法”、“后退法”、“逐步回归法”，这些方法各有优缺点，而逐步回归法因计算简便、结果更接近于实际而最受推崇。

1.1 逐步回归模型的基本思想

回归分析主要是研究客观事物变量之间的统计关系，是建立在对客观事物进行大量试验和观察的基础上，来寻找隐藏在那些看上去是不确定的现象中的规律。在实际问题中，建立回归模型时，遇到的关键问题就是如何确定回归自变量，为了得到准确的回归模型，自变量的选取应该尽可能的全面。回归自变量之间会存在一定的关系，而且对因变量的显著性程度也是不一样的。逐步回归模型的基本思想即：将自变量一个一个引入，每引入一个变量，对已选入的变量要进行逐个检验，当原引入变量由于后面变量的引入而变得不再显著时，要将其剔除。引入一个变量或从回归方程中剔除一个变量，为逐步回归中的一步，每一步都要进行F检验[3]，以确保每次引入新的变量之前回归方程中只包含显著性变量。这个过程反复进行，直到既无显著的自变量选入方程，也无不显著的变量从回归方程中剔除为止。

1.2 数学模型

设（xi1，xi2，…，xip；yi），i=1，2，…，n是变量（x1，x2，…，xp；y）的一组观测值，则线性回归模型可表示为yi= β0+β1xi1+β2xi2+…+βpxip+εi，i=1，2，…，n；其中随机变量y为被解释变量（因变量），x1，x2，…，xp为p个解释变量（自变量），β0，β1，β2，…，βp为回归系数，εi为相互独立并且服从N（0，σ2）的随机误差。

1.3 回归模型参数变量的选择方法

选取自变量时，一方面，尽量不遗漏包含所有重要信息的解释变量；另一方面，遵守参数最少原则，使得自变量尽可能少。因为当自变量过多时回归方程会变得复杂，影响回归速度；参数不足时则会影响回归方程的准确性。

1.4 多元线性回归模型的显著性检验

多元线性回归模型的显著性检验包括回归方程的显著性检验和回归系数的显著性检验。

1.4.1 回归方程的显著性检验

在实际问题的研究中，不能事先断定随机变量y与变量x1，x2，…，xp之间确有线性关系，因此，在求出线性回归方程之后，需要对方程进行显著性检验。使用F检验，目的是要检验自变量x1，x2，…，xp从整体上对随机变量y是否有明显的影响。提出假设H0：β1=β2= …=βP=0，如果H0被接受，则表明随机变量y与变量x1，x2，…，xp的线性回归模型没有意义。

为了构建检验H0所用的F统计量，使用总离差平方和分解方法，将正态随机变量y1，y2，…，yn的偏差平方和分解为

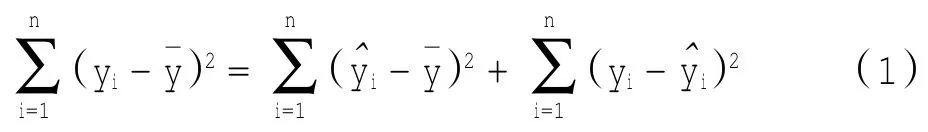
在正态假设下，当原假设H0：β1=β2=…=βP=0成立时，F服从自由度为（p，n-p-1）的F分布。对于给定的显著水平α，当F＞Fα（p，n-p-1），拒绝假设H0，说明回归方程显著，x与y有显著的线性关系，F值越大，越显著；

1.4.2 回归系数的显著性

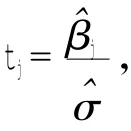
在实际的软件计算中，一种简便的方法是根据概率值p与显著性水平α的比较来判断，若p＜α，拒绝假设H0，说明回归方程显著，x与y有显著的线性关系，p值越小，回归方程越显著，所以本研究中将配合使用以上三种显著性的判别法作为判断的依据。

1.5 消除多重共线性

在建模过程中，考虑的自变量很多，而这些自变量之间完全不相关的情形是很少见的，所以产生多重共线性是难免的。而多重共线性违背了多元线性回归模型的基本假设，如果模型中两个自变量具有线性相关性，如x1=γx2，此时x1和x2前的参数β1、β2并不反映各自与因变量之间的结构关系，而是反映它们对因变量的共同影响，从而使β1、β2失去了意义，直接影响到最小二乘法的应用效果，降低了回归方程的应用价值。

为此使用方差扩大因子法来消除多重共线性，方差扩大因子，记为VIF，VIF的大小反映了自变量之间是否存在多重共线性[3]。经验表明，当VIFj≥10时，就说明自变量xj与其余自变量之间有着严重的多重共线性。当回归方程中的全部自变量都通过显著性检验后，回归方程中仍有严重的多重共线性，这时，我们应该把方差扩大因子最大者所对应的自变量首先剔除，再重新建立回归方程，反复此过程直到回归方程中不再出现严重的多重共线性为止。

2 飞机爬升阶段发动机燃油流量回归模型

2.1 数据准备

2.1.1 数据来源

以B777-200飞机选装的2台PW4077D发动机的20个航班数据作为研究样本（总样本个数大约为12 000），分别建立左发燃油流量和右发燃油流量与影响燃油流量的参数（自变量）之间的回归模型；另外有5个航班的数据作为预测验证样本。

2.1.2 航段划分

爬升阶段处于起飞阶段和巡航阶段中间，从起飞到爬升阶段，压气机转速突然增加然后在一个范围内波动，此过程持续的时间很短，而且环境因素和飞机自身参数的变化都比较大，将会使回归模型出现较大的误差，实际拟合发现，在这种情况下回归模型不显著，因此这个过渡阶段在建立模型先不予考虑。对于本次研究的B777-200型飞机，从对20个样本数据综合分析以及其他研究人员在此方面的经验可知，以飞行高度对爬升阶段进行界定，简单、合理。飞机爬升阶段的飞行高度范围为

其中：H为飞机的飞行高度（ft）。

2.1.3 气路参数相似修正

根据航空发动机相关原理可知，同一台发动机在不同工作条件下，其主要性能参数差别很大，所以不同航班的原始性能数据通常无法直接用于相互的比较分析，所以有必要将它们换算成标准大气条件下（P0=101 325 Pa，T0=288.15 K）的通用特性[4-5]，将标准大气状态下的相似参数称为换算参数，可用下标“cor”表示

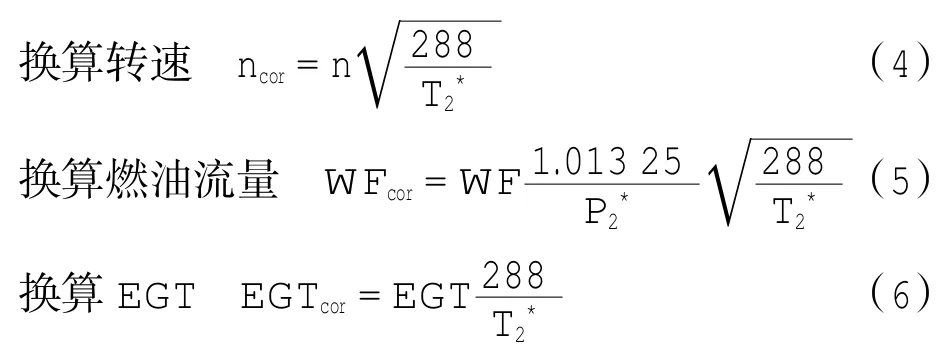
其中：T2*为发动机压气机进口总温（K）；P2*为发动机压气机进口总压（bar）。

2.1.4 自变量参数的选取及数据平滑

参考B777-200飞机性能手册[6]，根据航空发动机的工作原理，初步选取以下参数作为飞机爬升阶段发动机燃油流量的影响因素：飞机飞行高度H（x1）、马赫数Ma（x2）、换算低压转子转速N1cor（x3）、飞机俯仰角度PITCH（x4）、空气静温SAT（x5）、修正空速CAS（x6）、压气机进口压力P2（x7）、压气机进口温度T2（x8）、压气机出口温度T3（x9）、燃烧室压力BP（x10）、2.5放气活门开度25BP（x11）、换算高压转子转速N2cor（x12）、压比EPR （x13）、油门杆角度TRA（x14）、换算飞机排气温度EGTcor（x15）、飞机总质量M（x16）。

2.2 飞机爬升阶段燃油流量模型

以处于左发位置的某发动机在爬升阶段燃油流量WFcor（因变量）为例，选取以上16种影响发动机燃油流量的因素作为初始输入值，取显著性水平α= 0.05，应用SPSS分析软件，采取逐步回归法建立回归模型。

在所有同时满足F检验和t检验的回归模型中，依据F值越大显著性越好的原则，选取模型9，其F= 46 839.5为所有模型中最大的，即方程显著性最好，具体参数如表1所示。

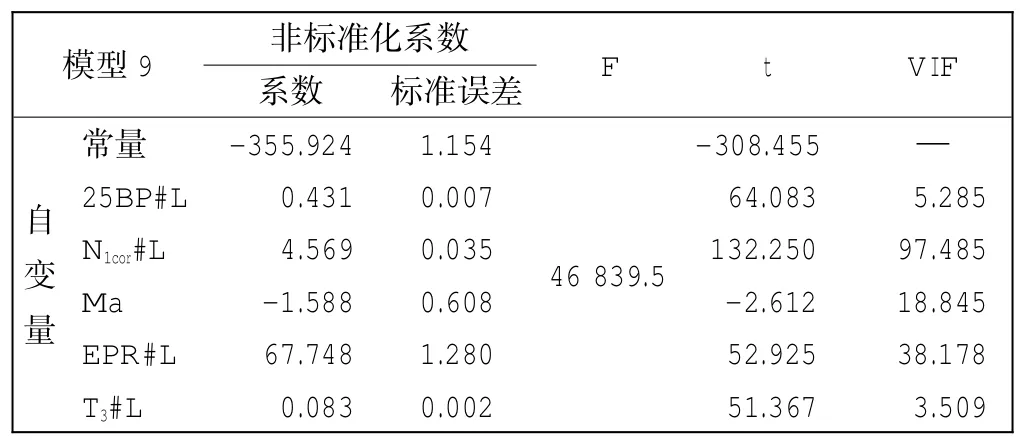
表1 初选模型的参数值Tab.1Parameter values of primary model

但是此模型存在严重的多重共线性，依据前文所述的方法，应该剔除VIF值最大的一个自变量再进行逐步回归。由发动机原理可知，N1cor、EPR都是航空发动机的推力表征量，两者的相关性极高，因此可选其一作为回归模型中的自变量，这里剔除N1cor，采用逐步回归法再次建立发动机燃油流量的回归模型，依据此方法，直到消除模型的多重共线性。

最终得到的模型参数如表2所示。经过分析，此回归方程和回归系数更加显著，并且VIFj＜10，无多重共线性。回归自变量分别为马赫数Ma（x2）、压气机出口温度T3（x9）和压比EPR（x13）。因此最终左发燃油流量的回归模型为

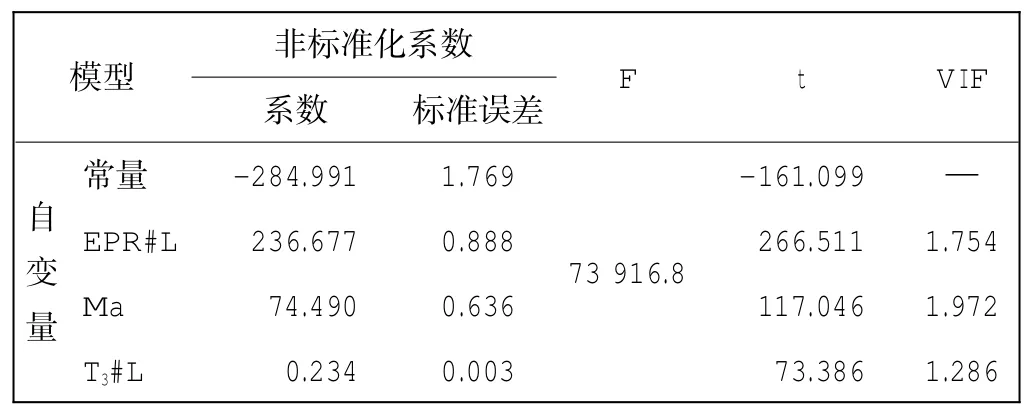
表2 最终模型的参数值Tab.2Parameter values of final model

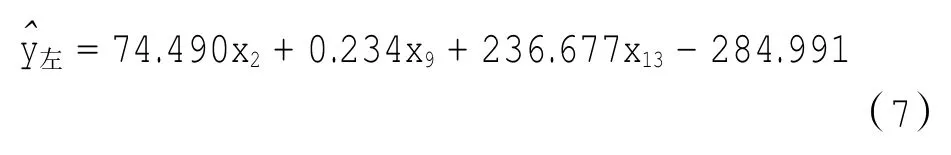
式中：y^左为左发爬升阶段燃油流量的拟合值。

按照同样的方法和步骤，建立右发爬升阶段燃油流量（WFcor）的回归模型，回归方程及回归系数分别满足F检验和t检验，并且VIFj＜10，即回归方程和回归系数高度显著，无多重共线性。最终右发燃油流量的回归模型为

式中：y^右为右发爬升阶段燃油流量的拟合值。

3 模型分析及验证

由上述模型可以知道，发动机燃油流量的解释变量为马赫数Ma（x2）、压气机出口温度T3（x9）和压比EPR（x13），分析如下：

飞机在爬升阶段，通常用马赫数来表征飞行速度，而马赫数的增大是由发动机燃油流量的不断增加来实现的，而发动机燃油流量的增加，一方面增加了推力和飞行马赫数；另一方面提供了飞机不断爬升所需要的升力；

压比（EPR）是一个至关重要的发动机推力控制参数，PW4000型发动机在正常工作期间，其推力控制方式一般采取EPR方式[7-8]，即EPR保持一个相对不变的数值，要求的EPR值由推力杆角度（TRA）决定，并由飞机和发动机的其他状态参数进行修正，依据TRA计算的EPR同实际的EPR相比较的差值决定燃油流量的调整值；

压气机出口温度T3是发动机性能的重要监控参数，T3不仅决定发动机的工作状态，而且反映发动机所承受的热负荷。

综上所述，此回归模型的3个自变量参数基本上涵盖了燃油流量的影响因素。

另取5次航班爬升阶段的记录数据（约3 000条）作为本模型的验证样本，得到左、右两台发动机燃油流量的实际值与预测值的变化曲线图。选取其中2次航班的预测图，如图1～图3所示，图中实线代表飞机在爬升阶段发动机燃油流量的真实值，虚线代表飞机在爬升阶段燃油流量的预测值。其中080709次航班（如图1和图2所示），在爬升阶段使用模型预测得到的发动机燃油流量预测值与真实值之间的误差很小，预测比较理想；但是，080708次航班（如图3所示）拟合的效果并不理想。

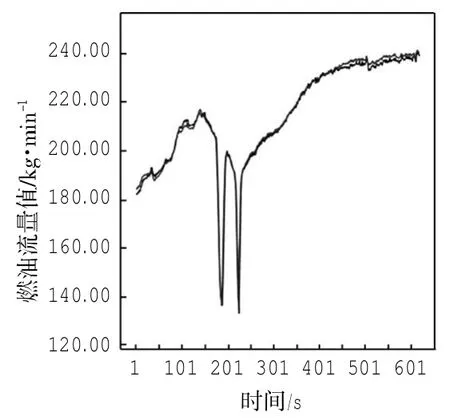
图1080709 左发燃油流量对比曲线图Fig.1080709 Left engine fuel flow comparison graph

图2080709 右发燃油流量对比曲线图Fig.2080709 Right engine fuel flow comparison graph

图3080708 左发燃油流量对比曲线图Fig.3080708 Left engine fuel flow comparison graph

分析可知，样本中B777-200飞机的航线一般为北京至香港或者北京至广州的较长航线，巡航高度一般在38 000 ft左右，而该架飞机080708次航班为北京至上海的中短航线，其巡航高度为33 000 ft，由于航程比较短，各个飞行阶段的范围都相对缩小，不符合本文对爬升阶段的界定。

4 结语

运用多元统计分析中的逐步回归法，对B777-200飞机选装的PW4077D发动机的QAR数据进行深入分析研究，建立了爬升阶段燃油流量的回归模型。经过分析验证，模型正确、可信，各项指标均通过检验，并且得到了很好的预测效果，为PW4077D发动机燃油控制规律的研究奠定了基础，通过燃油流量的监控和预测，实现对发动机的状态监控和预测。此种建立回归模型的方法可以应用于其他型号、其他航线飞机的燃油流量回归模型的建立，由于飞机燃油流量取决于发动机的控制规律、自身参数以及大气参数，而不同飞行阶段的控制规律、参数变化规律不尽相同，所以使用此方法得出的回归模型，仅适用于特定航段的B777-200飞机。

[1]刘洋.基于关联规则挖掘的PW4077D发动机放气活门控制规律研究[J].科技传播，2011（16）：238-239.

[2]王克宏，唐世建.航空发动机控制规律数值分析验证[J].燃气涡轮实验与研究，2009，22（4）：43-47.

[3]汪冬华.多元统计分析与SPSS的应用[M].上海：华东理工出版社，2010.

[4]瞿红春，林兆福.民用航空燃气涡轮发动机原理[M].北京：兵器工业出版社，2006.

[5]周百正.QAR数据处理系统的设计与实现[D].天津：中国民航大学，2011.

[6]Boeing777 System Schematic Manual[G].Chapter73，Jul.2000.

[7]杨晓军，赵宏利，曲春刚，等.民用航空发动机控制系统[M].天津：中国民航大学，2011.

[8]SUN JIANGGUO.Advanced Multivariable Control Systems of Aeroengines[M].北京：北京航空航天大学出版社，2005.

（责任编辑：杨媛媛）

Research of fuel flow regression model of aircraft climb phase based on QAR

CAO Hui-ling，JIA Chao
（College of Aeronautical Engineering，CAUC，Tianjin 300300，China）

QAR can be used for aircraft and engine performance analysis,recording abundant key flight data such as fuel flow.Taking PW4077D engine installed in B777-200 as researching object,the author analyzes its QAR data in details,builds fuel flow regression model during aircraft climbing phase with multiple regression analysis approach,and verifies the accuracy with actual data.The results build basis for comprehensive research of engine fuel flow controlling laws,help to monitor and predict engine fuel flow and improve aircraft safety and economy.

aircraft engine；fuel flow；regression model；QAR

T233.2

A

1674-5590（2013）03-00031-05

2012-06-06；

2012-09-12

中国民航大学科研基金项目（08CAUC-E01）

曹惠玲（1962—），女，河北唐山人，教授，工学博士，研究方向为航空发动机性能分析与故障诊断.