基于干扰观测器的舵阻摇PID控制

巩舒超, 宋立忠, 田英俊

（海军工程大学，武汉 430033）

0 引言

船舶在海面上航行时，由于受到风浪和洋流的影响，将产生摇摆运动，这对于船舶的安全性、适居性以及战斗舰艇的作战性能都有很大的影响，因此，如何经济有效地减小船舶在航行中的摇摆运动就成了人们关注和研究的焦点。

舵阻摇是一项比较新的阻摇技术，与减摇鳍、减摇水仓等设备相比，它具有初期投资少，系统体积小，阻摇效果可观的优点，并且舵阻摇对操纵系统的动态特性和船的流体动力特性的要求一般也容易得到满足[1]，只需对舵机进行改造就能实现阻摇，且系统关闭后不会产生拖曳和噪声，对声纳装置的影响较小，这一点对于战斗舰艇来说，尤为重要[2]，因此，舵阻摇技术愈来愈受到重视。

在目前的研究中，舵阻摇控制器一般都采用传统的PID算法，由于舵阻摇系统具有强烈的不确定性、非线性特性，船舶的形状，排水量，航速，舵叶的面积等因素都能强烈影响舵阻摇系统的有效性，所以，采用常规PID控制器的阻摇效果不够理想，有时甚至会影响船舶运动航向航迹的控制。为此，本文在传统舵阻摇PID控制器的基础上进行改进研究，设计了海浪干扰观测器，将外部力矩干扰和模型参数变化造成的实际控制对象和名义模型输出的差异，全部等效到输入端，即观测出等效干扰，并在控制中引入等效补偿，实现对干扰的抑制，以期取得较好的控制效果。

1 船舶舵阻摇模型

船舶在海上的运动情况，可以描述成相对于1个惯性参考系的运动，船舶的运动具有6个自由度，即纵荡、横荡、垂荡、艏摇、横摇、纵摇。其非线性运动方程如下[3]：

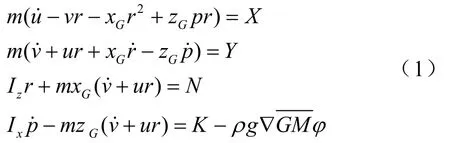
其中，m是船舶质量，u是纵荡速度，v是横荡速度，r是艏摇角速度，p是横摇角速度，xG,zG分别是船舶的质心G到附体坐标系Axyz的x轴和z轴的距离，Ix,Iz分别是船舶对于附体坐标系Axyz的x轴和z轴的转动惯量，X,Y分别表示作用在惯性坐标系中x,y轴上的外力，N,K分别表示外力对于惯性坐标系中z,x轴上的力矩，▽表示船舶的排水量，g是重力加速度，ρ是水的密度，表示恢复力臂，φ表示船舶的横摇角。

X,Y,N,K都是船舶运动变量和控制变量的非线性函数[3]：

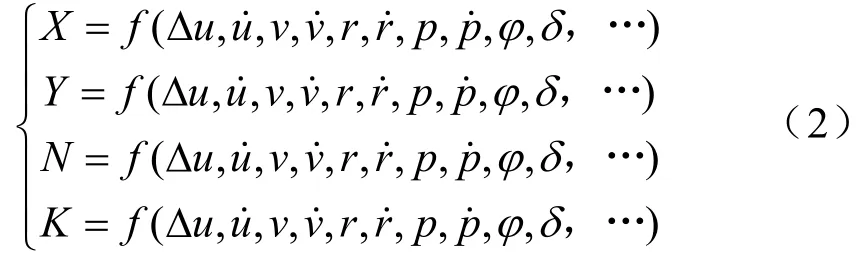
其中，δ表示舵角。其余变量同式(1)一致。显然，直接使用非线性模型来设计控制器是很困难的，因此在舵阻摇控制设计中，通常是要将模型线性化，将式(2)利用泰勒级数展开，忽略一阶以上的高次项[3]，即可得到线性模型(3)。在该线性模型中未考虑纵荡。

其中，E,F,G见参考文献[4]。

E是惯性力系数矩阵，F是粘性力系数矩阵，G是舵力系数矩阵。显然，系统的系数矩阵A=E-1F，输入矩阵B=E-1G，我们将舵角δ作为输入。横摇角φ作为输出，则能得到系统关于φ-δ的输入输出表达式[4](4)。

其中，Kδp是横摇方程的增益系数，Kvp是横摇方程的耦合因子，ωφ是海浪对横摇的扰动，ξ是阻尼系数，ωn是横摇频率，v'为由舵机引起的横票速度，是一个中间变量，Kδv表示横摇和艏摇的耦合增益系数，Tv是二者耦合的惯性系数，引入v'是为了将横摇和艏摇状态方程解耦。

船舶参数如下：Tv= 78/U，Kvp= 0.21U，Kδp=-0 .0014U2，ωn= 0.63，Kδv=0.01U，ζn= 0.064 +0.0038U。

取船速U= 7.8m/s，得到：

2 基于干扰观测器的舵阻摇PID控制器设计

设计的基于干扰观测器的舵阻摇PID控制系统如图1所示，图中虚线框内的部分为干扰观测器。

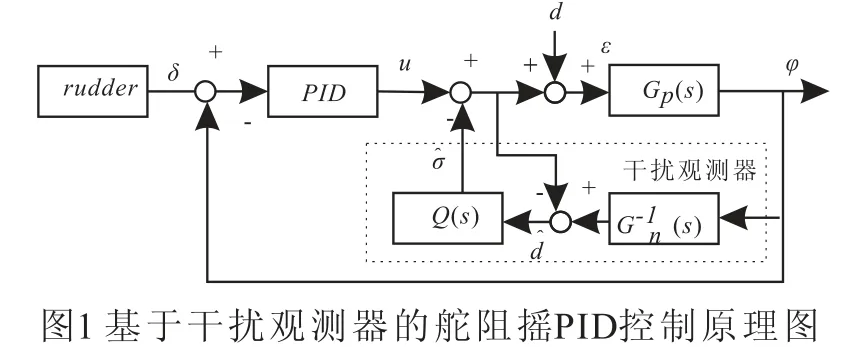
图中的Gp(s)是船舶横摇模型，Gn(s)是船舶横摇的名义模型，d是等效干扰，u是PID控制器的输出，是观测干扰，Q(s)是干扰观测器中的低通滤波器，是干扰观测值经过低通滤波器后的输出，u是PID输出，δ是舵角。显然，系统的输入

对于图-1，由梅森公式可得到u到横摇角以及外部干扰d到横摇角的传递函数。

由图-1可以看出，观测干扰值为：

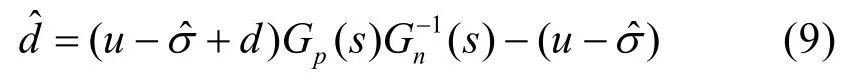
理想情况下，建立系统的模型应该与其名义模型一致，那么上式就化简为=d，可见，理想情况下，将观测干扰值引入到系统的输入端，可以完全消除干扰d的影响。遗憾的是，这在实际应用中是不可能实现的，因为无法对研究对象进行精确建模。因此，图-1中的系统模型的频率特性对名义模型存在一个乘性摄动Δ (s)，通常情况下，是ω的增函数，当频率增加时，系统的不确定性也随之增大。他们之间的关系表示为：

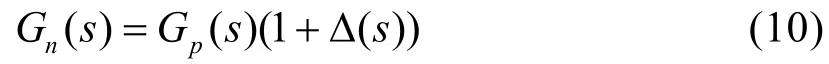
再来考察传递函数Guφ(s)和Gdφ(s)：利用补灵敏度函数和鲁棒稳定性定理分析传递函数Guφ(s)。

系统的灵敏度函数为：

则补灵敏度函数为：

有鲁棒稳定性定理[6]可知：系统鲁棒稳定的充分必要条件是：

可见，通过设计合适的低通滤波器Q(s)，就可以满足系统的鲁棒性要求。亦即：

Q(s)设计原则需满足Q(s)Gn-1(s)为正则[7]，即Q(s)的相对阶不能低于Gn(s)的相对阶；其次，参数τ的取值决定了Q(s)的带宽，τ越小，带宽越宽，此时认为Q(s)≈ 1，Gdφ(s) =0，系统具有较强的对外部干扰的抑制能力，Q(s)带宽的设计则应该在满足干扰器的鲁棒稳定性和干扰抑制能力之间权衡考虑，。

根据以上结论，设计Q(s)为分母为三阶，分子为一阶的低通滤波器，表达形式为：

仿真表明，在τ= 0.001附近时，系统的鲁棒稳定性和抗干扰能力均能得到较好的实现。

3 仿真研究

在该仿真中，系统的名义模型如下，以体现与实际建模之间的差异：

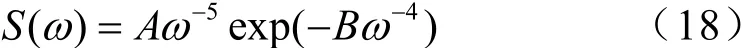
其中：

g重力加速度，ν—海面19.4 m高处的风速。

图2表示采用常规PID控制下的船舶阻摇效果仿真。其中，实线表示采用常规PID控制器时船舶的横摇角曲线，虚线表示船舶的自然横摇角曲线。图3表示具有干扰观测器的PID控制器的阻摇效果仿真，实线表示采用具有干扰观测器的舵阻摇PID控制器时船舶的横摇角曲线，虚线表示船舶自然横摇角曲线。

显然，两种舵阻摇控制器都能明显减小船舶横摇强度，但加入干扰观测器的方案阻摇效果更好一些，为便于比较，图4中，实线表示加入具有干扰观测器的PID控制舵阻摇时船舶的横摇角，虚线表示加入常规PID舵阻摇控制器时船舶的横摇角，仿真结果如下：

由以上的仿真结果图看出，直接应用PID控制器时的阻摇率大概为40%，而在同等条件下，加入干扰观测器的PID阻摇率在60%以上。干扰观测器的加入能更好地降低船舶的横摇幅度，增强阻摇效果，表现出了良好的抗风浪干扰的能力。

4 结束语

虽然PID控制目前仍然是工程实际中应用最广泛的控制算法，但对于强非线性、不确定系统，其控制效果难以令人满意，本文将PID控制器与干扰观测器结合用于舵阻摇控制，能够有效地减弱横摇幅度，表现出了良好的鲁棒性。

[1] 张忠宝．基于斜舵的船舶减摇控制研究[D]．哈尔滨：哈尔滨工程大学，2009.

[2] 葛德宏，高企孝，陈永冰等. 舰船舵阻摇技术的研究现状及展望[J]． 舰船科学技术，2007, 8(4).

[3] 杨承恩，贾欣乐，毕英君．船舶舵阻摇及其鲁棒控制[M]．大连：大连海事大学出版社，2000：29-30．

[4] Van A J，Van der K P G M and Van N L H R．Rudder roll stabilization for ships[J]．Automatic, 1990,26(4)：679-690．

[5] 刘金琨．先进PID控制MATLAB仿真[M]. 北京：电子工业出版社，2011．

[6] J．C．Doyle，B．Francis．A．R．Feedback control theory[M]．Macmillan Publishing Co., 1992.

[7] 柴光远，赵鹏兵，程旭等．干扰观测PID 控制在电液位置伺服系统中的应用[J]．控制与检测，2009，(11)．

[8] 朱洪华，蔡建立．不规则海浪的仿真[J]. 人工智能及识别技术, 2007．