基于ANSYS软件计算电机结构模态
韦春健, 史振宇
(1. 海军驻桂林地区军事代表室,广东湛江 524009;2. 海军驻武汉四三八厂军事代表室,武汉 430060)
0 引言
电机结构的模态是其固有特性,与电机结构的运动性能有很大联系,电机结构的振动频率要远离模态频率,振动方向要避开模态振型的方向,否则容易引起共振损坏电机。因此,掌握电机结构的模态信息对于电机的科学使用是非常重要的,ANSYS有限元分析软件可以用于计算电机的模态频率和模态振型(模态向量),效果良好,计算过程一般包括四个步骤:建模、加载和求解、扩展模态以及查看结果。
有限元求解模态的理论基础来源于结构系统振动的一般微分方程[1,2]:
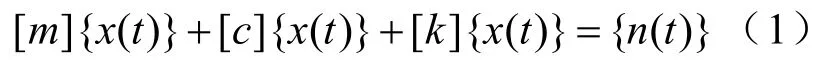
讨论一种特殊情况,即无阻尼的自由振动,[c]=0,{n(t)}=0,其运动微分方程为:
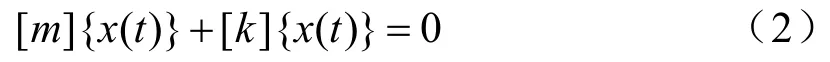
假定为简谐振动,经过变换处理可得到包含模态频率ω和模态振型{u}的振动方程:
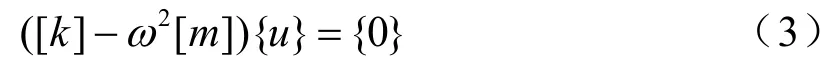
上式是一个关于{u}的n元线性齐次方程组,其具有非零解的条件是系数行列式等于零,即

此方程称为系统频率方程,方程左边是一个n阶行列式,展开得到n次方程,则必有n个根。讨论一般情况,如果系统的质量矩阵和刚度矩阵都是正定的实对称矩阵,在数学上可以证明该n次方程的n个根均为正实数,它们对应振动系统的n个模态频率。将各个根ωr2(r=1,2,…,n)代入式(4)得到各个对应的解{u(r)},称为系统的模态振型。模态频率ωr和模态振型{u(r)}称为振动系统的第r阶模态,它表征了系统的一种基本运动模式,即同步运动,同时也是简谐运动。
依据上述的基本理论,有限元计算时,将结构整体划分为有限个质量单元,建立各单元之间互相作用的振动方程,设定初始条件,即可求解该结构的模态。为简化问题,以某卧式电机的端盖(见图1)为例,利用ANSYS软件求解其模态信息,然后与锤击实验得到的模态信息作比较。

1 电机端盖模态计算
1) 建模
用三维建模软件建立端盖的三维几何模型[3],然后导入ANSYS划分网格,建立有限元模型[3,4](见图2)。有限元模型在实物模型的基础上做一些修改,删除了装配端盖用的四个伸出块,它们对端盖整体模态影响不大,删除后方便划分网格,尽量使网格整齐对称、均匀顺滑,网格划分的质量往往对最终的求解有很大影响,应尽量用六面体单元,网格粗细可根据要求结果的精确程度确定,然而并非网格越精细越好,有时反而会浪费资源,增加求解时间。采用SOLID185划分网格,材料是HT200,看作各向同性,取密度为7200 kg/m3,弹性模量为`1.0×1011Pa,泊松比为0.27。

图2 端盖有限元模型
2) 加载与求解
选择分析类型为Modal,用默认的Block Lanczos法提取模态,提取40阶模态(不包括刚体模态),采用缺省的一致质量矩阵,提取端盖自由状态下的模态。设置完成后,开始求解[6,7]。
3) 模态扩展
把振型写入结果文件中,在后处理器中查看模态振型。指定扩展的模态阶数为20,频率范围为50~3000 Hz,模态范围不从零开始,是为了去掉刚体模态。若想继续扩展其它频率范围的模态,可重新设置,每次扩展处理结果都存为单独的载荷步。
4) 查看结果
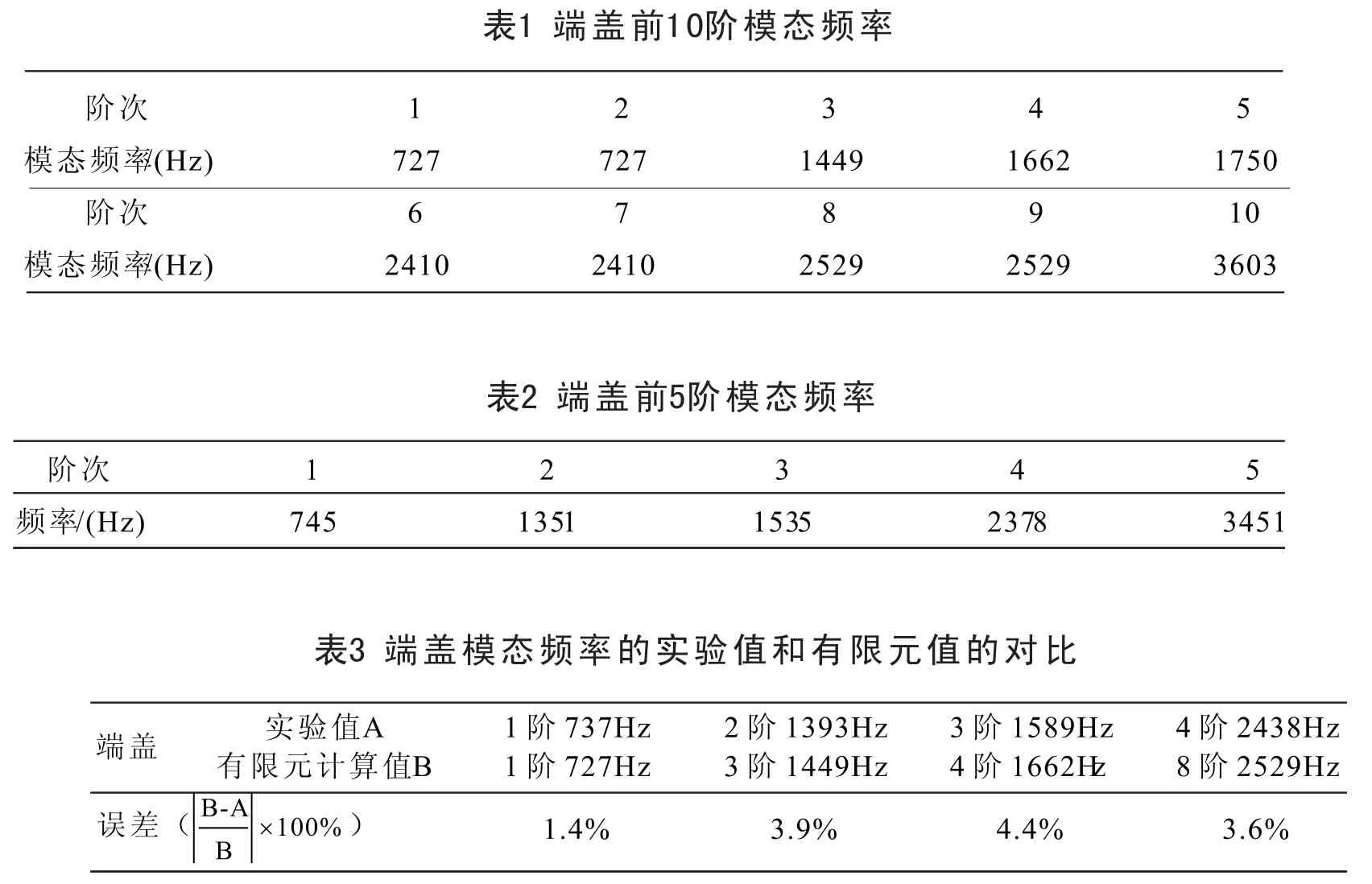
表1为端盖前10阶模态频率(不包括刚体模态)。端盖振型分为径向和轴向,因为卧式电机端盖主要是径向受力,所以只关注径向的振型。查看端盖前10阶振型发现径向振型从椭圆、三角形到四边形的顺序变化,符合结构振型阶次变化的规律。由于结构对称,从模态频率和振型上看,有些不同阶次的模态是一致的。
2 锤击法测电机端盖模态
用锤击法测量电机端盖径向的模态,并与ANSYS软件的计算结果作比较,验证计算的正确性和可行性。锤击法测量模态,激励力为脉冲信号,在频域上是宽频信号,相当于在电机端盖上施加各种频率的激励信号,分析系统的频响函数,找出频响函数与模态参数的联系[8]。通过实验测量端盖径向的模态频率和模态振型,建立振动模型如图3所示。实验得到端盖前5阶模态频率(见表2)和模态振型[9],振型也是从椭圆、三角形到四边形的顺序变化。

图2 端盖振动模型
3 验证
把有限元计算与实验测量得到的相同模态进行对比,如表3所示,相同的模态只选出其中一种。从表中可知,实验和有限元得到的结果相差不大。
4 结论
?
通过选择卧式电机端盖模型,利用ANSYS软件进行模态的有限元计算,建立合适的三维模型是关键,为优化模型在实物模型的基础上进行必要的等同和修改,计算时选择合适的网格划分方式和单元种类有利于快速和准确求解。最后,通过与锤击实验的比较,验证了基于ANSYS软件计算电机结构模态是行之有效的方法。
[1] 师汉民.机械振动系统-分析·测试·建模·对策(上册)(第二版)[M].武汉:华中科技大学出版社, 2004.
[2] 李德葆,陆秋海.工程振动试验分析[M].北京:清华大学出版社,2004.
[3] Autodesk, Inc.Autodesk Inventor 2009基础培训教程[M].北京:化学工业出版社,2009.
[4] 邓凡平.ANSYS10.0有限元分析自学手册[M].北京:人民邮电出版社,2007.
[5] 小枫工作室.最新经典ANSYS及Workbench教程[M].北京:电子工业出版社,2004.
[6] 张洪信,赵清海.ANSYS有限元完全自学手册[M].北京:机械工业出版社,2008.
[7] 张红松,胡仁喜,康士廷.ANSYS12.0有限元分析从入门到精通[M].北京:机械工业出版社,2010.
[8] 沃德·海伦,斯蒂芬·拉门兹,波尔·萨斯(著).模态分析理论与试验[M].北京:北京理工大学出版社,2001.
[9] 傅志方,华宏星.模态分析理论与应用[M].上海:上海交通大学出版社,2000.

