IGBT有源逆变器在高压大功率电机转子侧变频调速系统中的应用研究

李 棋，王钦若，彭 义

（广东工业大学自动化学院，广东广州 510006）

0 引言

随着电力电子学科和电力元件的发展，大功率电机转子侧变频调速技术有了进一步的发展，在传统转子变频调速系统中，逆变器产生电压的大小随着晶闸管触发角大小变化而变化，转子侧附加电动势变化改变转子电流，以此改变电机转速。斩波式调速系统是在整流与逆变回路之间中加入IGBT 斩波器使晶闸管的触发角固定在30°，但由于最小触发角的存在，想要进一步提高功率因数有一定的困难，还会使系统发生逆变颠覆的问题。

针对这些问题，从系统拓扑结构加以改进，用IGBT有源逆变器代替晶闸管逆变器，采用SVPWM 技术，使逆变器网侧电流波形接近正弦波，减小谐波“污染”，并且可以提供容性无功来补偿系统产生的感性无功[1]，那么整个系统的功率因数便会提高，同时克服了逆变颠覆的缺点。

1 传统斩波式变频调速系统工作原理

传统斩波式变频调速系统主电路如图1 所示。

图1 传统斩波变频调速系统主电路

图中CH 为IGBT 组成的BOOST 直流斩波器，其工作在开关状态。UR 为二极管组成的三相不可控整流器，UI 为可控硅组成的三相逆变器，TAW 为网侧变压器。调节电机转速实际上是通过调节转子电流的大小，也即是要调整转子附加电动势的大小，而附加电动势的大小会随直流斩波器两端电压的变化而变，因此改变斩波器开通和关断的时间便可调节电机转速。二极管D主要起到隔离整流和逆变回路的作用，电抗器L1起滤波和储能作用，直流斩波器的缓冲网络由电容C、电抗器L2和二极管组成，直流侧大电容C 主要起到能量缓冲作用，电抗器L2的作用是防止有源逆变器UI电流断流。

有源逆变器TI的触发角β 固定在最小触发角βmin，其大小不跟随电机转速的变化而变化，因此可有效地减少系统对无功的吸收以便提高系统功率因数，因此UI为固定电压：

其中：U2T为逆变器交流侧电压。

设IGBT 直流斩波器的开关周期为T，斩波器开通时间为τ，当其开通时，三相整流桥UR 和IGBT逆变器产生的附加电动势都被短路，此时二极管D 将整流和逆变电压隔离开，主回路电流Id上升；斩波器关断时间为T-τ，当其断开时，电动机工作在转子变频调速状态下，此时二极管D导通将整流和逆变接通，电抗器L1释放电能并向电容充电，主回路电流Id下降[2]。根据CH直流斩波器前后电压相等可得出：

从式（2）可以看出，UD的大小由CH 直流斩波器开通时间τ 决定。

其中：E20为电机转子开路电压；s为电机转差率。

由式（1）、（2）、（3）得：

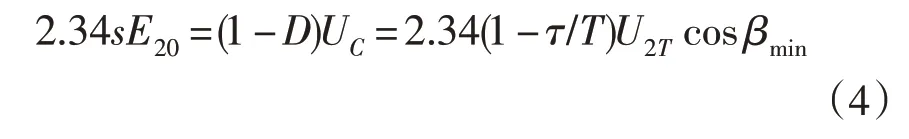
因此，电机的转速n 与直流斩波器的开通时间τ 的关系为：

其中，n 为理想空载转速；n0为异步电动机的同步转速。

在转子侧变频调速时，理想空载转速n 小于异步电动机的同步转速。逆变器UI的触发角变化时，电机转速n 和转差率s会随其变化，触发角β变大时，转速n 变大，转差率s 变小。从式（5）还可看出，电机转速还会随着斩波器的占空比的变化而改变。在系统中，一般把触发角β 取为30°。

2 IGBT 有源逆变器在转子侧变频调速系统中的应用

由于传统调速系统采用晶闸管组成有源逆变器，那么系统的功率因数会因晶闸管的最小触发角的存在得不到进一步的提高，还会产生谐波“污染”和逆变颠覆故障等问题。

为了解决这些问题，从系统拓扑结构加以改进，用IGBT有源逆变器代替晶闸管逆变器，采用SVPWM 技术，使逆变器网侧电流波形接近正弦波，减小谐波“污染”，并且可以提供容性无功来补偿系统产生的感性无功[3]，那么整个系统的功率因数便会提高，同时克服了逆变颠覆的缺点。

2.1 三相电压型IGBT有源逆变器的工作原理

电压型IGBT逆变电路拓扑结构如图2所示。

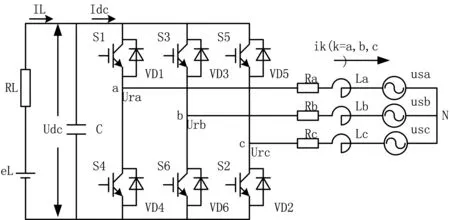
图2 三相电压型IGBT有源逆变器拓扑结构

usk（k=a，b，c）为网侧电压，Lk（k=a，b，c）为外接电感及电机漏感之和，Rk（k=a，b，c）为等效电阻，el为直流侧电压，urk（k=a，b，c）为逆变器产生的基波电压。IGBT有源逆变器的控制原理为：保证直流侧电压Udc为恒定值，尽可能使网侧电流与电压同相位并近似正弦波，以此提高系统功率因数并减小谐波。

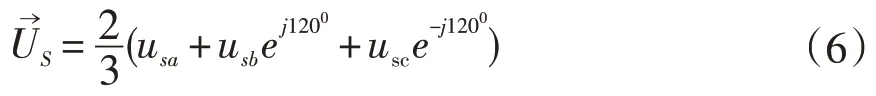
电网侧电流矢量表示为：

逆变器产生的基波电压矢量表示为：

逆变器网侧的矢量方程表示为：

用图3 所示的空间矢量图表示矢量方程（9），可以看出，空间各向量以工频角速度w作逆时针旋转且保持相对位置不变[5]。如果可以很好地控制电网侧电流的相位，便可以有效控制IGBT有源逆变器的运行象限。

图3 逆变器网侧空间矢量图

2.2 IGBT有源逆变器的静态解耦模型

为建立简单的数学模型以方便控制系统的设计，只考虑逆变器的低频分量[6]，根据图2 可得IGBT逆变器的低频方程为：

从（10）可看出，三相IGBT逆变器网侧各物理量是随时间变化的交流量，这种物理量会对控制系统的设计造成不便。为此，把它转换成dq 坐标系下的方程，在dq 坐标系下各物理量以电网基波频率同步旋转[7]，可得：

从式（11）可看出，控制器的设计会因d 、q 轴电流耦合而变得困难。网侧电流相位的控制可以通过采用前馈解耦控制算法来实现[8]，可得ud，uq的控制方程：

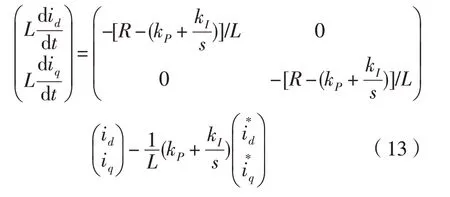
由此可见，通过前馈解耦控制实现了id、iq相互独立。基于前馈解耦原理的IGBT有源逆变器控制系统框图如图4所示。

图4 控制系统框图

3 采用SVPWM 算法的IGBT 逆变器仿真实验及结论

根据三相电压型IGBT 有源逆变器的拓扑结构，采用SVPWM 控制算法，采用静态解耦直接电流控制策略对其进行仿真。仿真中所用到的参数为：直流电压为幅值650V的直流电压源，交流电网电压峰值311V，频率50Hz，交流侧电感30mH，电感的等效电阻和功率开关损耗等效电阻的合并值取0.02 Ω，直流侧电容1 000 μF ，开关频率为10 kH。

图5 IGBT有源逆变SIMULINK仿真模型

图6 整流状态时A相电压电流波形

图7 逆变状态时A相电压电流波形

图8 整流到逆变网侧A相电流电压波形

从图6～9 可看出，采用静态电流解耦控制策略，可很好地控制网侧电流相位，使其近似为正弦波，IGBT逆变器处于整流工作状态时，电网侧电流波形接近正弦波并于电压相位同相，系统功率因数为1，当其处于逆变工作状态时，网侧电压电流相位相反，系统功率因数为-1，采用IGBT有源逆变还可有效减小谐波电流，其THD为0.46%。

图9 整流状态时FFT分析图

本文将传统高压电机转子变频调速系统中的晶闸管逆变器替换为IGBT有源逆变器，改善电网侧电流波形质量，降低网侧电流的谐波，提高功率因数，彻底解决了电网故障导致逆变颠覆而损坏设备的问题。

［1］姚锐，李柯，王兵书.SVPWM在内反馈斩波串调系统中的应用研究［J］.化工自动化及仪表，2010，37（7）：72-75.

［2］于精卫.斩波式内反馈串级调速系统的设计［D］.内蒙古：内蒙古科技大学，2008.

［3］张崇巍，张兴.PWM整流器及其控制［M］.北京：机械工业出版社，2004.

［4］刘观起，孙会水，万军.基于IGBT斩波控制的内反馈串级调速系统的研究［J］.电力科学与工程，2008（1）：37-40.

［5］庞科旺，袁文华，刘丽丽.三相电压型PWM整流器在内反馈斩波串级调速中的应用研究［J］.电气自动化，2008（5）：16-18.

［6］殷海蒙，高艳霞，江友华.大功率交流电动机转子变频调速系统的分析［J］.电机与控制应用，2006，33（6）：51-54.

［7］孔鹏.PWM逆变技术在内反馈串级调速系统中的应用［D］.保定：华北电力大学，2008.

［8］张少伟.SVPWM 在有源逆变中的研究与应用［D］.保定：华北电力大学，2008.