基于FPGA的永磁同步电机矢量控制IC的设计
覃曾攀,曾岳南,吴礼智
(广东工业大学自动化学院,广东广州 510006)
0 引言
随着电力电子技术的发展、新材料的出现、微处理器水平的不断提高和交流控制理论研究不断地深入,永磁同步电机在航空航天、数控机床、加工制造、机器人等方面获得了广泛应用。由于数字控制技术的发展,使得数字控制器在处理速度、抗干扰、系统稳定性等方面都是模拟控制器无法比拟的[1-2]。近年来,基于FPGA 的电机控制得到越来越多的关注,它不仅实现了软件需求和硬件设计的完美集合,还实现了高速与灵活性的完美结合,使其超越了ASIC器件的性能和规模,也超越了传统意义上的FPGA的概念[3]。
本文研究了交流永磁同步电机矢量控制策略,PI 调节器,电流采样,速度以及位置的测量,并通过硬件描述语言实现各个模块的设计。整 个 系 统 的 设 计 是 利 用 Cyclone ⅢEP3C25Q240C8N 型FPGA 作为主控芯片,实现交流永磁同步电机的双闭环控制。
1 永磁同步电机数学模型及其矢量控制策略
1.1 永磁同步电机在同步旋转坐标系中的数学模型
永磁同步电机在同步旋转坐标系中的电压方程:

永磁同步电机电磁转矩方程为:

Ld、Lq为电机直轴、交轴同步电感,Rs为电机定子电阻,Pn为电机定子绕组极对数,ψf为转子永磁体磁极的励磁磁链,ω 为电机转速,Te为电机电磁转矩。对于表贴式永磁同步电机,在电机定子上接三相对称正弦波电源,在旋转坐标系中的变量都为直流变量,并且由转矩方程式直接可以看出电机的输出转矩与电流iq呈线性关系,只需要控制iq的大小就可以控制电机的输出转矩。电机矢量控制结构如图1所示。

图1 永磁同步电机矢量控制结构图
1.2 转子磁场定向的矢量控制原理与架构
永磁同步电机矢量的基本思想是建立旋转坐标变换对id、iq轴的解耦,最终实现了相似于直流电机转矩的控制方法来控制永磁同步电机转矩,获得和直流电机相当的性能[4]。图2 为定子电流空间矢量示意图,abc 为三相静止坐标系,αβ为两相静止坐标系,dq 为两相旋转坐标系。定义电流空间矢量is为:

图2 定子电流空间矢量图

由三相静止坐标系到两相静止坐标系(Clark变换)可得:

再由两相静止坐标系到两相旋转坐标系(Park变换)可得:

相应的从两相旋转坐标系到两相静止坐标系(Park-1变换)可表示为:

其中θ 为转子角位置。当采用id=0的控制方式时,定子电流矢量is落在q 轴上,这时转矩方程为:
Te=1.5Pnψfiq
其中Pn为电机定子绕组极对数,ψf为永磁磁链为恒值。从转矩方程可以看出,通过坐标变换,永磁同步电机的电磁转矩与电流iq成正比,控制iq就能直接控制电磁转矩。其矢量控制结构图如图1所示。
2 控制IC架构与电路设计
系统硬件逻辑结构框图为图3 所示,其主要包括矢量变换模块、SVPWM 调制模块、电流采样模块、转速测量模块、位置检测模块、转速和电流PI 调节模块6 大部分。
2.1 矢量变换模块
矢量变换模块包括clark、park、park 逆变换,而在park 和park 逆变换中存在正余弦的计算,而在数字信号处理中正余弦的计算一般有三种方法:查表法、泰勒级数法、CORDIC 算法[6]。从占用资源、精度两方面考虑,因为CORDIC 算法在精度比较高的情况下所占用资源少,故采用CORDIC算法,其迭代公式为:


图3 系统硬件逻辑结构框图

其中,当zi≥0 时,Si=1;否则,Si=-1。设k是一个无理常数,其表达式为:

当n →∞时,k≈0.607 253。实验采用有符号18 位的Q14 格式来表示[0,2 π]范围的弧度值,从迭代公式可以看出,输出结果同时完成了cos θ 和sin θ 的运算。其数字逻辑电路结构框图如图4所示。

图4 CORDIC算法数字逻辑电路结构框图
2.2 SVPWM调制模块
SVPWM调制模块主要由扇区判断、基本电压矢量作用时间计算、电压空间矢量切换点计算、载波生产模块、PWM生成模块,死区设置模块等几部分组成[7]。其数字逻辑电路结构框图如图5所示。
2.3 电流采样模块
系统采用2 个电压型霍尔传感器检测两相电流,再通过跟随、滤波、放大、抬升将双极性的电压信号转化为单极性的范围在0至3V电压之后经过TLC549CP芯片进行模数转换送入FPGA主芯片中,由于采用的AD转换芯片在AD转换后的数据是串行数据,故在FPGA 中还必须进行串行到并行的转换,而且之后还需转化为双极性实际电流的大小并进行标幺化,其数字逻辑电路结构框图如图6 所示,其中虚线框图中串并转换模块主要输出AD芯片需要的片选信号和时钟信号,其输入为两相电流AD转换后的数字信号。

图5 SVPWM调制模块结构框图
2.4 转速、位置检测模块
转速、位置检测主要是通过复合式光电编码器发出的A、B、Z、U、V、W 六路信号来计算,电机每转一圈A、B 每相输出2 500 个脉冲,电机逆时针旋转A相超前B相90°,顺时针旋转时,B相超前A 相90°。电机每转一圈输出一个Z 脉冲,用于角度清零,消除累加误差。U、V、W三相用于电机的初始定位。为提高测量转速和位置的精确度将A、B脉冲4倍频,故电机转一圈可发出10 000 个脉冲,编码器每发出一个脉冲电机旋转0.288的电角度,这样通过检测脉冲个数就可以计算电机的位置。转速测量采用位置差分方法,其数学表达式:

图6 电流采样模块结构图

其中,w(k)为第k次采样的角速度,θ(k)为第k 次采样的电机角度,θ(k-1)为第k-1 次采样的电机角度,T为采样时间。
2.5 转速、电流PI调节器模块
数字PI 调节器有位置式和增量式两种算法,位置型PI调节器的计算需要进行累加,计算量较大,不便于程序的实现,而且需要用到过去的误差值,容易产生大的累加误差;增量型PI调节器不需要做累加,控制量的确定仅与最近两次的误差值有关,计算量少,计算精度更高[5]。故本文采用增量型PI调节器。
离散化后的PI表达式如下所示:
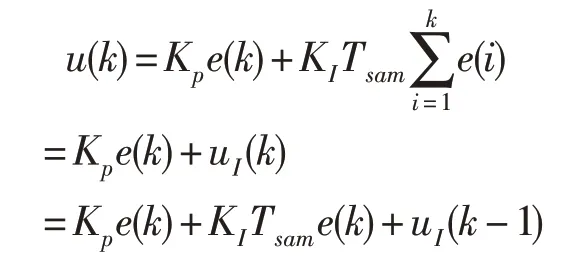
其中Kp为比例系数,KI为积分系数,Tsam为采样周期。其数字逻辑结构框图如图7所示。

图7 PI调节器数字逻辑电路框图
3 实验结果
以上介绍的模块都采用VHDL 语言编写,并在FPGA(EP3C25Q240C8N)上实现,系统编译报告如表1 所示。本系统的测试电机额定功率为750 W,额定转速为3 000 r/min,额定电流为3.58 A,光电编码线数为2 500PPR,永磁同步电机。系统电流环的采样频率和IGBT的开关频率采用10 kHz,开关死区时间为4 μs ,转速环的采样频率为2.5 kHz。从SVPWM 输出的上桥臂信号图可以看出开关周期为100 μs ,图8为V相和W相的电流波形,图9 为电机开始启动转速给定指令为900 r/min 的动态响应波形。实验表明系统具有良好的动态响应。

表1 编译报告

图8 V、W相电流波形图
4 结论
系统采用以FPGA 为控制芯片,根据矢量控制理论,SVPWM调制算法,id=0的控制策略实现了永磁同步电机的双闭环调速。整个系统的设计以全硬件的方式实现,使得电流环的响应速度非常快,整个系统的动态响应性能提高,保证了系统的实时性。同时系统设计采用Altera公司的Cyclone ⅢEP3C25Q240C8N型具有丰富的逻辑资源和应用I/O,使得系统在提高控制精度和升级成为可能。

图9 转速波形图
[1]Naizheng Cui,Cuijie Yang,Yajing Liu,and Pinzhi Zhao.Development of an FPGA-Based high performance Servo Drive System for PMSM [A].ISSCAA 2006,19-21.
[2]S.Carbone,V.Delli Colli.Design and Implementation of High performance FPGA Control for Permanent Magnet SynchronousMotor [A].IEEEINMIC,Nov.2009,2901-2906.
[3]Zhaoyong Zhou,Tiecai Li.FPGA Realization of a high-performance Servo Controller for PMSM [A].APEC 2004,Vol.3,1604-1609.
[4]Abdolreza Esmaeli,Li Bo,Sun Li.A novel AC Servo System Implementation [A].IEEE INMIC,Nov.2005,1-5.
[5]Qi Hui,Zhao Ya.Design and Realization of PMSM Vector Control IP Core Based on FPGA [A].IEEE INMIC,Nov.2006,1325-1328.
[6]Zhou Zhu.Implementation and Studies on Direct Digital Frequency Synthesis based on CORDIC Algorithm[M].National University of Defense Technology,December,2005.
[7]梁文军,杨世锡,魏义敏.基于FPGA 的转子振动信号整周期等相位采样控制方法[J].机电工程,2011(2):148-152.
[8]Zhou Yuan,Xu Fei-peng,Zhou Zhao-yong.Realization of an FPGABased SVPWM Controller[A].IPEMC′06,Vol.1,Aug.2006,1-5.

