基于暂态信号频域分析的故障测距方法

余亮，李志强

（1.国电南瑞科技股份有限公司，南京市 210061；2.晋城煤业集团，山西省 晋城市 048006）

0 引 言

非有效接地方式在一点接地时，系统中未构成短路回路，故障信号较为微弱难于获取，有些特殊电网甚至含有大量的线缆混合线路，线路参数的统一计算也成为亟待解决的问题之一。随着智能电网的提出，有效解决配电网接地故障定位的问题，并及时恢复供电线路的正常运行对电网的稳定运行具有积极意义。已在一些配电网应用的故障定位方法有：（1）S信号注入法，根据对某一特定频率信号的寻踪实现故障定点，该方法受信号注入功率非稳定接地故障的限制；（2）馈线终端装置 （feeder terminal unit，FTU）配电网自动化系统，能实现故障区段的定位，但需要的投入较大，限制了其应用［1］。同时，一些应用于输电线路故障测距的方法也逐渐用来解决配电网定位问题。如：行波测距［2－4］，它利用计算接近光速的故障波头往返于故障区段的时间来实现故障测距，它需要数字信号处理（digital signal processing，DSP）技术、高速数据采集技术、通信技术的支持。暂态信号频谱分析的方法［5－10］，是利用某一行波波阻抗不连续点（包括故障点）到故障测量点的距离与特征频率的大小成反比，通过计算反应故障信号特征频率方法计算故障距离，其测距的关键是故障点对应的特征频率的有效判定。本文通过连续小波变换（continuous wavelet transform，CWT）分析，提取故障位置对应的特征频率，并以一条简单电缆为例搭建仿真模型，验证此方法的可行性。

1 利用小波分析提取故障特征频率

在无损传输线路中，故障产生时，相当于故障瞬间故障点处附加了一个与故障处电压大小相等、方向相反的附加电源，此暂态量行波分别向线路两端传播，其传播速度由线路的分布参数所决定。由于分布电容、电感、电阻的存在，故障产生的行波不仅在波阻抗不连续点发生折、反射，同时在传播过程中，行波的幅值会减小，相位也会发生改变。

文献［8］阐述了利用行波特征频率故障测距的方法，该方法利用拓扑中各个波阻抗不连续点到观测点形成的不同路径长度与某些频率形成特定的数学关系来计算故障位置，实际上反映了行波在特定传输线路往返的周期性特点，其表现为某一特征频率。其数学关系由下式来确定。

式中：n为测量端再次获得同一极性的行波浪涌，其在特定路径传播所往返的次数。当不连续点的反射系数接近＋1时，即传播至线路端点，n为2；当不连续点的反射系数接近－1时，即传播至故障点或分支点，n为4；L为某一路径的实际长度；vi为第i模的波速；p为某一路径。由于在实际的传输线路中，存在线路间的耦合，同一路径的波速会有不同，以下计算均是针对经过Clark变换后1模的参数确定的波速。路径的特征频率反映了不连续点的特性。

连续小波分析通过连续改变尺度a，来改变小波母函数的时域与频域的局部特征，与待分析信号做相似比较运算得到的小波系数。小波函数与待分析信号的相似度越高，待分析信号的时域突变性、频域性越能被敏感地反映出来。在本方案进行故障测距时利用小波变换的系数对故障暂态进行频域分析，通过测定频谱图的极大值确定特征频率，若母小波函数是待分析信号的一部分，显然其相似程度最大，频谱图中的幅值大，极大值明显，更容易分辨，提高了母小波函数对不同故障的适应性。

2 故障定位实现方法

2.1 母小波的建立

传统的小波函数在对暂态信号分析时，频率的分辨率比较低，对于不同的故障分析结果不可靠，当线路较为复杂，特征频率比较多时，某些特征频率无法分辨或是极大值不突出导致故障测距无法进行。同时由于暂态信号随时间推移快速地衰减，所以将故障信号的初始部分作为待建立的母小波数据，从理论上反映了母小波函数与故障暂态信号的最大相似性。

对故障暂态信号的初始部分及其所划定的母小波部分定义如下

式中tcf是故障暂态波形采样的触发时刻，tf0－tcf与1／f0相对应，在固定的时间段tw内，计算相应的最小频率f0，同时时间窗口tf0－tcf应该为所要提取的最大周期信号（最小频率）的整数倍，即满足以下条件：

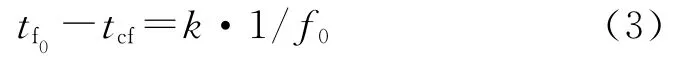
2.2 连续小波变换的数字实现其特征频率的提取

小波变换的过程中，所采用的母小波函数必须满足容许性条件，即

式中ψ（ω）为ψ（t）傅里叶变换后的结果。从式（4）可以得出其充分条件：（1）ψ（t）是具有正负交替性质的波形，即在支撑域边界快速衰减至0，即，其中，［－t0，t0］为ψ（t）的支撑域。

建立了上述小波函数以后，就可以将其与采集到的离散信号进行连续小波计算，离散点的连续小波变换由式（5）定义。

式中：Δt为对应的采样周期，ψT（t）为所建立母小波的转置矩阵；a是由所需要分析的频率范围决定的，即f＝f0／a·fs，其中f0为小波母函数的中心频率，fs为采样频率。

对小波变换的结果定义小波系数能量，即处在同一尺度下小波变换系数的平方和，它反映了每个频率成分的权重，即

式中：C（a，b）T是小波系数向量的转置矩阵。

3 PSCAD／EMTDC仿真验证

3.1 EMTDC模型的建立

图1显示了一个简单的电缆线路拓扑的仿真模型。其中，线路结构为一条出线，整个线路的电压等级为35kV，高压侧的变压器变比为110／35，低压侧的变压器变比为35／10，电缆线路中线路的参数模型选用Frequency Dependent（Phase）Model，这个模型对于故障的暂态信号与基波的谐波信号的仿真较为精确。依据电缆线路的参数，根据公式计算行波1模的波速，并由公式修正波速，以10kHz为中心频率，将1模的波速做近似处理，其值为vα＝1.49×108m／s，故障点距离为1.5km，过渡电阻为100Ω。

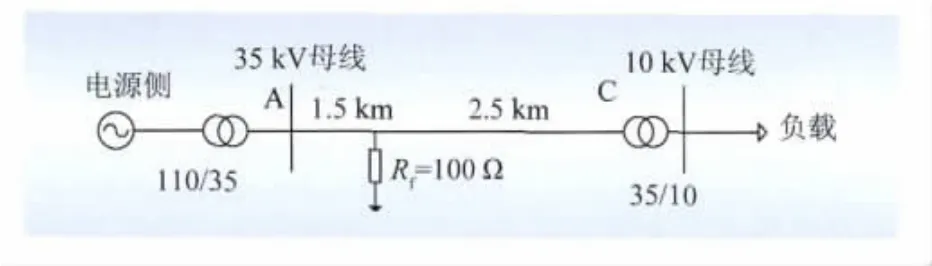
图1 PSCAD／EMTDC仿真模型Fig.1 Simulation model of PSCAD／EMTDC

3.2 仿真实验结果

A相接地故障后的波形见图2，该图是在35kV母线侧，采集三相的电压量，经Clark变换后的α模量。

图2 故障发生后的α模量与小波母函数的截取Fig.2 Modulusαand mother wavelet function after fault event

图2显示了由故障暂态截取的自建立母小波的图形。根据上文的描述，截取故障发生后一段时间的故障波形，并进行相应的小波母函数容许性条件改造。图3绘出了图2中截取波形部分得到的小波母函数，虚线部分表示叠加的双端指数衰减函数。

图3 自建立小波函数Fig.3 Wavelet function built from transient

根据公式定义的小波系数能量的值，利用自建立母小波对暂态波形做连续小波变换，可以得到相应的频谱图，如图4所示，得到相应的特征频率为f＝23.9kHz，根据前述的电缆线路的线模波速，计算故障距离d＝1.56km，绝对误差为600m。

利用PSCAD／EMTDC计算了在不同故障距离的自建立母小波分析的结果，如图4虚线与短划线所示，计算得到的故障距离分别为d＝2.48km和3.48km，绝对误差为200m，由此可见，自建立母小波对于简单的线路分析效果精确。

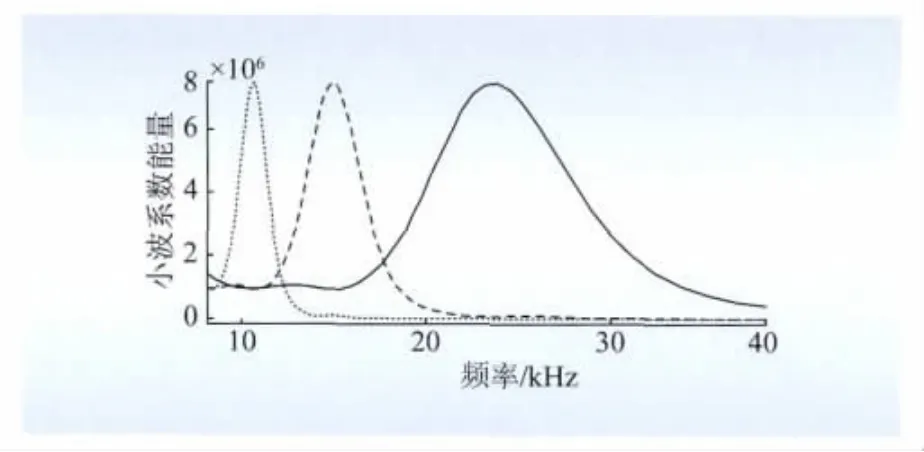
图4 小波系数能量谱Fig.4 Energy spectrum of wavelet coefficients

4 结 语

本文提出了一种利用提取暂态信号进行故障测距的方法，通过定义小波系数能量，并根据故障信号定义小波函数，准确提取故障对应的特征频率，获取故障距离。本文提出的基于特征频率的故障定位方法与传统的行波测距方法相比，不需要行波到达波头的辨识，且在满足采样定理的原则上，对硬件的要求不高，原理上易于实现。该方法对于线路拓扑较为简单的特征频率的提取较为准确，当线路拓扑复杂时，相近的频率有时会有混叠的现象，需要进一步研究，提高频率提取的分辨程度。

［1］杜刚，刘迅，苏高峰.基于FTU和“S”信号注入法的配电网接地故障定位技术的研究［J］.电力系统保护与控制，2010，38（12）：73－76.

［2］张帆，潘贞存，张慧芬，等.基于方向行波的小电流接地系统故障选线［J］.中国电机工程学报，2007，27（12）：70－75.

［3］陈羽，刘东，徐丙垠.基于IEC61850的行波测距装置建模［J］.电力系统自动化，2013，37（2）：1－5.

［4］邬林勇，何正友，钱清泉.一种提取行波自然频率的单端故障测距方法［J］.中国电机工程学报，2008，28（10）：69－75.

［5］董新洲，葛耀中，徐丙垠.利用暂态电流行波的输电线路故障测距研究［J］.中国电机工程学报，1999，19（4）：76－80.

［6］邬林勇，何正友，钱清泉.单端行波故障测距的频域方法［J］.中国电机工程学报，2008，28（25）：99－104.

［7］黄旭勇，张文魁，刘沛.电网行波故障定位装置的最优化配置及其改进算法 ［J］.电力自动化设备，2010，30（1）：41－44.

［8］夏璐璐，何正友，李小鹏，等.基于行波固有频率和经验模态分解的混合线路故障测距方法［J］.电力系统自动化，2010，34（18）：67－73.

［9］谢民.220kV电网行波测距系统组网运行实践探讨［J］.电力自动化设备，2010，30（5）：136－141.

［10］陈玉林，陈允平，龚庆武.电缆故障在线测距中高速同步采集卡精确时标获取方法［J］.电力自动化设备，2006，26（10）：35－41.