基于非线性回归分析的特高压直流线路杆塔质量计算

林清海，杨博，陈鹏，任伟

（1.山东电力工程咨询院有限公司，济南市 250013；2.国家电网公司运行分公司，北京市 100052）

0 引 言

在输电线路杆塔优化排位设计中，随时需要调用杆塔质量（下称塔重）指标等资料，而准确地计算各种方案的铁塔质量需花费大量的时间和精力。通常估算铁塔塔重的方法是在已有施工图设计塔重的基础上，只对某种塔型的某种呼高进行塔重估算，而同一型式的不同呼高及荷载条件下的塔重，则采用公式近似估算，但误差较大。国内外有关塔重估算研究结果发现，塔重与铁塔呼高和其可能的作用荷载变化值有关。近年来西南电力设计院提出了铁塔设计荷载与塔重的力矩关系式［1］，并对其影响系数进行了取值分析，其主要优点是对输电线路铁塔通过归纳、比较、适配，确立设计荷载与塔重的关系式，为塔重估算方法提供依据。但该关系式存在局限性，如：不适用于特高压直流线路，关系式中影响塔重的变量过多，操作繁琐，易出错。

回归分析是通过建立数理统计模型来研究变量之间相互关系的一种数理统计方法，对相应的变量进行预测和控制，是进行计量分析的主要工具［2］。Matlab因其面向矩阵的编程特性、出色的图形处理功能、应用广泛的模块集合工具箱以及图形仿真界面而在研究、解决工程和数学问题中得到广泛应用［3］。在Matlab中列举了多种常见的回归分析函数，可轻松实现对数理统计模型的构建。因此，本文以“±800kV铁塔典设”［4］的塔型塔重作为数据样本，用回归分析的方法，借助Matlab发现杆塔质量与杆塔呼高、荷载条件［5－6］之间的规律性，建立塔重估算数学模型；对不同导地线、气象区、地形和海拔高度的模块塔重样本，按地形和海拔高度进行分类，采用回归分析的方法，整理归纳出塔重估算关系式，并与实际典设塔重作比较，其误差小、精度高；在已知地形和海拔高度的条件下，就可以采用杆塔呼高和荷载条件计算塔重，实用有效；本文选取哈郑线工程中含有多种导线、气象区、地形和海拔等的设计标段，采用塔重估算关系式计算施工标段总塔重，并与实际塔重作比较，其误差较小，进一步验证了关系式的准确性。

1 基本原理及实施方法

1.1 非线性多元回归分析原理

非线性多元回归分析的算法［7］如下：

（1）非线性最小二乘法求取参数估计值。该方法以误差平方和最小为准则来估计非线性静态模型参数。设y＝f（x，θ），式中θ是参数。这里的非线性是指对参数θ的非线性模型。在估计参数时，模型的关系式f是已知的，经过n次实验取得样本数据（x1，y1），（x2，y2），…，（xn，yn）。估计参数（或称目标函数）选为模型的误差平方和。

非线性最小二乘法就是求使Q达到极小的参数估计值θ，并采用复杂的优化迭代算法来求解。Matlab中的非线性曲线拟合函数nlinfit和lsqnonlin等使用高斯－牛顿迭代算法可以很好地实现非线性拟合并求解参数估计值和置信区间的功能。

（2）回归方程的显著性检验。本文采用求取R2可决系数的方法对非线性回归方程进行显著性检验，具体是：回归方程中反映因变量n个观察值与其均值的总离差称为总平方和（SST）；反映自变量x变化对因变量y取值变化的影响称为回归平方和（SSR）；反映除自变量x以外的其他因素对因变量y取值的影响称为残差平方和（SSE），三者关系如下式。

R2可决系数反映了回归的拟合程度，取值范围在 ［0，1］之间。若R2→1，说明回归方程拟合的程度好；若R2→0，说明回归拟合的程度差。R2的平方根R通常称为复相关系数，可以看作是因变量y与变量x之间相关关系及密切程度的一种度量。

1.2 塔重估算非线性多元回归分析的算法

杆塔的塔重可用下式表示［1］：

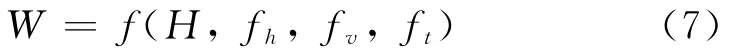
式中：W 为塔重指标；H为杆塔呼高；fh为水平荷载；fv为垂直荷载；ft为纵向荷载（直线塔时此值为0）。从上式的函数可确定任何一个参数变化对塔重的影响。

本文以“±800kV铁塔典设”的塔型塔重作为数据样本，用回归分析的方法，借助Matlab发现杆塔质量与杆塔呼高、荷载条件之间的规律性，建立塔重估算数学模型。塔重估算回归分析的算法如图1所示。

图1 算法流程Fig.1 Algorithm flow

2 算例分析

2.1 数据样本的选取

首先以“±800kV铁塔典设”中通用设计模块8B2为样本进行算例分析，按照不同地形和海拔高度，对不同导地线、气象区的典设塔重样本，采用回归分析的方法进行分类归纳，借助Matlab发现杆塔质量与杆塔呼高、荷载条件之间的规律性，建立塔重估算数学模型，并对其进行准确性校验。

模块8B2主要技术条件：导线型号为6×JL／G3A－1000／45；地线型号为JLB20A－150；设计风速为33m／s；覆冰厚度为10mm；地形为平丘；海拔高度≤2300m。

模块8B2塔为干字型平丘塔，按平腿设计，直线塔悬垂串采用V型串，耐张塔跳线采用双V型鼠笼式硬跳；直线塔采用5塔方案，另加I型防串倒塔、II型跨越塔和II型直线转角塔，耐张塔采用4塔方案，即20°分档，4型塔取60°90°为1档。

2.2 杆塔质量与呼高的关系

杆塔塔重计算系统荷载等条件不变时，杆塔呼高越高则塔重也越大。为确定杆塔质量W与杆塔呼高h的关系式W＝f（h），首先运用Matlab对已知施工图塔重、杆塔呼高数据作散点图观察数据规律，然后确定其回归指数曲线模型，如图2所示。

图2 直线塔质量与呼高的关系散点图及回归曲线Fig.2 Scatter diagram and regression curve of relationship between supporting tower weight and height

图2表示了直线塔3种塔型的杆塔质量与呼高的指数关系。使用式（8）描述的指数关系来拟合塔重时，误差很小，其平均误差为0～2.4%，直线塔质量与呼高的关系用回归模型关系式表示。表1中给出了对该模型关系式的检验：在参数估计值95%置信区间下，可决系数R2为0.983，非常接近1，因此，使用该模型关系式进行拟合是合理的。

表1 直线塔质量与呼高回归关系式Tab.1 Regression relationship between supporting tower weight and height

表中：a、b为常数，对于不同塔型，a值不同，而b值基本一致。b值的范围为0.0147～0.0192，杆塔级间（1 m1级）比值为e0.0147×1＝1.015～e0.0192×1＝1.019，所以b值可采用加权平均法取一定值，此处b的平均值为0.0173，级间比值为1.017。

2.3 杆塔质量与荷载的关系

杆塔呼高条件不变时，直线塔设计水平荷载和垂直荷载越大则杆塔质量也越大。为了便于分析杆塔质量与荷载条件的关系，可选择一个杆塔呼高作为研究对象，这个呼高称为标准塔高。标准塔高取57 m时，不同塔型的塔重、各极导地线水平荷载（最大风工况）、垂直荷载（覆冰工况）之和如表2所示。

表2 直线塔质量与杆塔荷载关系表Tab.2 Supporting tower weight and load

为了得到杆塔质量和荷载的关系式，对表2中的W、fh、fv进行多元回归分析，运用Matlab分别作 W～fh，W～fv关系散点图及回归曲线，如图3所示，发现数据分布符合线性规律，从而确定其回归模型。

图3 直线塔质量（W）与荷载（fh，fv）的关系散点图及回归曲线Fig.3 Scatter diagram and regression curve of relationship between supporting tower weight（W）and load fh，fv

图3所示直线塔质量与荷载的关系，采用回归模型关系式可以表示为

使用式（10）描述的线性关系来拟合塔重时，误差很小，其拟合的平均误差为0.0%～7.7%，对该模型进行显著性检验，在参数估计值95%置信区间下，可决系数R2为0.951，非常接近1，因此使用该模型关系式进行拟合是合理的。

2.4 杆塔质量与呼高及荷载的关系

式（8）为直线塔荷载条件一定时杆塔质量与呼高的指数关系式，式（9）为标准塔高时杆塔质量与荷载条件的线性关系式，综合上述2式即得到杆塔质量与呼高、荷载条件的关系式

由于地形与塔腿设计有关，海拔高度与极间距离、悬垂V串间隙等控制塔头尺寸的因素有关，虽然以上两者在塔重中所占比例很小，但考虑到塔重估算的准确性，仍不宜忽略。因此本文按地形（平丘、山地）和海拔高度进行分类，选取“±800kV铁塔典设”中不同导地线（导线截面900mm2的8A模块、1000mm2的8B模块）、气象区、地形和海拔高度（≤2300m）等的非特殊塔型作为塔重样本；采用非线性多元回归分析的方法，整理并归纳出塔重估算关系式见表3。

表3 直线塔估重关系式样例Tab.3 Sample of estimation formula for supporting tower weight

利用表3塔重估算样例关系式可以在已知海拔高度和地形的情况下，通过杆塔呼高和荷载条件预测杆塔的重量。图4给出了采用估算关系式计算模块8B2直线塔的塔重结果与实际典设塔重的对比情况，由图4可见绝对误差在5%以内，且大部分误差在3%以内。

图4 直线塔各呼高估算塔重与实际塔重比较Fig.4 Comparison of supporting tower weight between estimation values based on different height and actual values

2.5 转角塔杆塔质量估算方法

由于转角塔的角度力一方面会导致水平荷载fh增加，另一方面会产生垂直于铁塔横担方向的纵向荷载ft，因此转角塔塔重受其转角角度影响很大［8－10］，其塔重估算数学模型关系式为

本文继续以“±800kV铁塔典设”的非特殊塔型作为塔重样本，采用非线性多元回归分析法，整理并归纳出塔重估算关系见表4。

表4 转角塔估重关系式样例Tab.4 Sample of estimation formula for angle tower weight

利用表4的塔重估算样例关系式可以在已知海拔高度（≤2300 m）和地形的情况下，通过杆塔呼高和荷载条件预测杆塔的重量，图5给出了采用估算关系式计算模块8B2转角塔的塔重结果与实际典设塔重的对比情况，由图5可见绝对误差在6%以内，且大部分误差在3%以内。

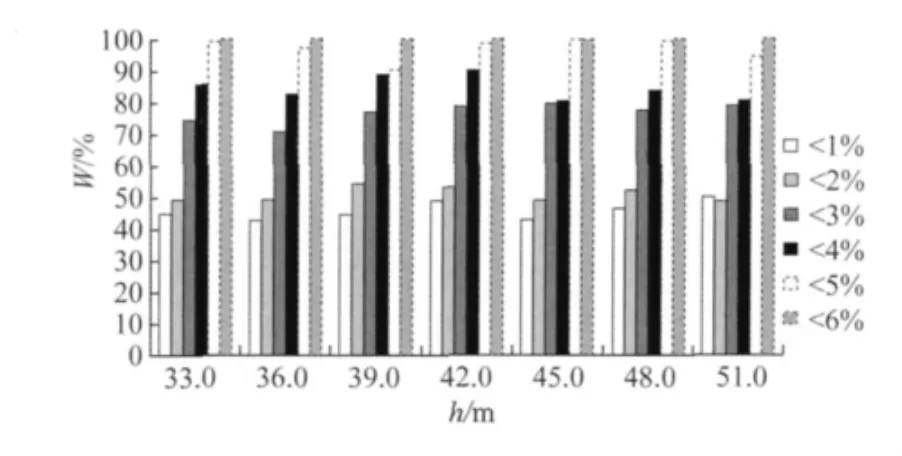
图5 转角塔各呼高估算塔重与施工图塔重比较Fig.5 Comparison of angle tower weight between estimation values based on different height and values in construction drawing

3 工程实例验证

为继续验证该塔重估算关系式，特选取哈郑线工程包7设计标段，其线路长度91.2km，设计条件如表5所示。

表5 哈郑线工程包7标段设计条件Tab.5 7th bid segment design condition of Hazheng transmission line project

计算不同导线型式的荷载，采用分类归纳的塔重估算关系式计算标段总塔重，并与施工图设计塔重作比较，如图6所示。直线塔总塔重误差小于3.3%；转角塔总塔重误差小于6.4%；标段总塔重误差小于4.5%，该误差对于设计方案比选及优化是可以接受的。

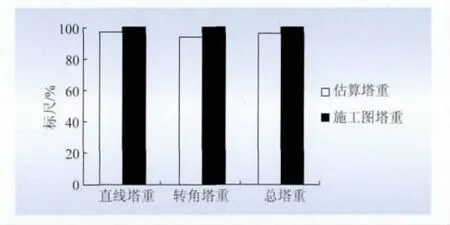
图6 设计标段估算塔重与施工图塔重比较Fig.6 Comparison of tower weight between estimation values in design segment and values in construction drawing

4 结 语

以“±800kV铁塔典设”的塔型塔重作为数据样本，用回归分析的方法，借助Matlab发现杆塔质量与杆塔呼高、荷载条件之间的规律性，建立了塔重估算数学模型关系式。

为便于使用，对不同导地线、气象区、地形和海拔高度的模块塔重样本，按地形和海拔高度进行分类，采用非线性多元回归分析的方法，整理并归纳出塔重估算关系式。因此，在已知地形和海拔高度的条件下，即可以使用杆塔呼高和荷载条件估算塔重。

估算塔重结果分别与实际典设塔重，实际哈郑线设计标段总塔重作比较，其误差小，精度高，因此该塔重估算的方法及关系式可用于设计方案的比选及优化。

［1］肖洪伟，肖兵，李力，等.输电线路铁塔设计荷载与塔重的关系式分析［J］.电力建设，2006，27（9）：4－6.

［2］龙永红.概率论与数理统计［M］.北京：高等教育出版社，2004：215－267.

［3］张德丰.MATLAB概率与数理统计分析［M］.北京：机械工业出版社，2010：233－260.

［4］刘振亚等.国家电网公司输变电工程±800kV特高压直流输电线路铁塔分册［M］.北京：中国电力出版社，2012.

［5］于刚，梁政平，李勇伟，等.±800kV直流架空输电线路设计规范（报批稿）［M］.北京：中国电力出版社，2012：18－24.

［6］张殿生，倪宗德，张洞明，等.电力工程高压送电线路设计手册［M］.北京：中国电力出版社，1999：166－206.

［7］Madsen K，Nielsen H B，Tingleff O，et al.Methods for non－linear least squares problems［R］.Denmark：Technical University of Denmark，2004.

［8］唐家德.基于MATLAB的非线性曲线拟合［J］.计算机与现代化，2008，154（6）：15－19.

［9］John H Mathews，Kurtis D Fink.数值方法：MATLAB版［M］.北京：电子工业出版社，2005：195－215.

［10］徐萃薇，孙绳武.计算方法引论［M］.北京：高等教育出版社，2002：62－85.