基于均匀圆阵的幅相误差自校正算法
鲁祖坤 高 鹰 肖 剑 石 宇
(1.空军航空大学 长春 130022;2.总参陆航部军事代表局 北京 100050)
1 引言
近年来,高分辨率的空间谱估计算法在雷达、声纳、移动通信等多个领域得到了广泛的应用,理论与实践应用表明,当阵列为理想模型的情况下,空间谱估计算法的性能十分优越,但是当阵列存在误差时,性能将明显下降,甚至失效[1,2]。在实际应用中由于生产工艺和施工技术等方面的影响,阵列误差往往难以避免,而大多数阵列误差都可归结为幅度和相位的误差,因此阵列幅相误差条件下的波达方向估计算法研究具有重要的现实意义[3,4]。均匀圆阵与均匀线阵相比,能够同时估计波达方向的俯仰角和方位角,具有更优的估计性能[5]。本文利用接收数据中信号子空间与噪声子空间正交的特点,对波达方向的角度和幅相误差值进行初步估计,根据初始估计值,再运用迭代的方法进行精确估计,无需初始值,为空间谱估计理论的广泛应用提供有益参考。
2 信号模型
2.1 阵列模型
均匀圆阵共有M个各向同性的阵元分布在一个半径为r的圆周上,在x-y-z坐标系中,均匀圆阵的中心位于坐标系的原点O上,信号的俯仰角和方位角分别用 φ 和 θ来表示,且 φ∈[0,π/2],θ∈[0,2π]。在均匀圆阵中,第i个阵元和圆心之间的连线与x轴之间的夹角为2πi/M;均匀圆阵的半径可以表示为r=λ/4sin(π/M),那么相邻两个阵元之间的距离为λ/2,λ为信号的载波波长。

图1 均匀圆阵模型
根据图1中的均匀圆阵模型,可以得到均匀圆阵的阵元接收信号的数学模型如下:

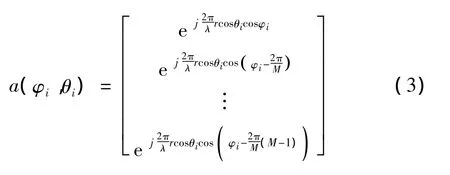
式(1)中,X(t)表示阵列在t时刻接收的观测数据;A表示空间阵列的导向矢量矩阵;S(t)为信号矢量,满足 S(t)= [s1(t),s2(t),…,sN(t)]T;N(t)为阵元噪声矢量,N(t)= [n1(t),n2(t),…,nM(t)]T,ni(i=1,2,…,M)为零均值、方差为 δ2的白噪声,且与信号源无关[6,7]。式(2)中N表示待估计的信源个数;式(3)中,i=1,2,…,M。
2.2 幅相误差模型
阵列幅相误差对阵列流形的幅度和相位产生扰动,设幅度误差对阵元i的扰动为μi,相位误差的扰动为ϑi,阵元1为参考阵元,认为无误差存在,因此幅相误差矢量可表示为:
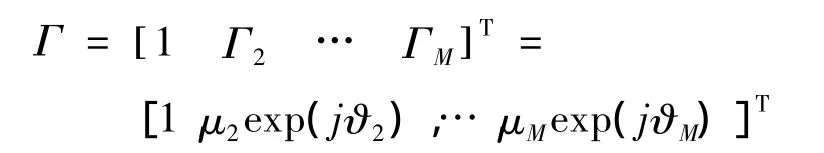
幅相误差对阵列流形的扰动,是通过标准导向矢量之前乘以幅相误差矢量的对角阵进行建模,误差存在时的导向矢量表示为:

阵列幅相误差情况下的阵列流形矩阵可表示为:

阵列接收的快拍数据可以表示为[8~10]:
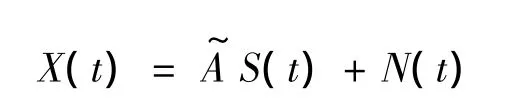
3 算法推导
考虑使用M个阵元的均匀圆阵(UCA)阵列天线对N个窄带正弦非相干信号进行接收,当阵列模型为理想情况时,接收数据快拍数为K,接收数据如式(1)所示,则协方差矩阵为[11]:

在实际应用中由于是有限次快拍,RXX不能准确获得,一般利用式(5)来近似估计:
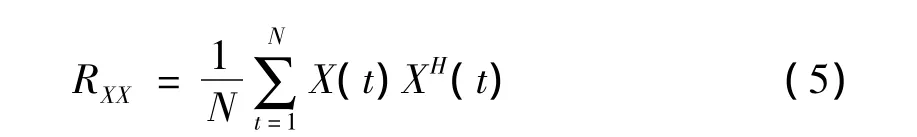

式(6)中∑为协方差矩阵特征值所组成的对角阵,根据特征值的大小,将∑ 分解为大特征值组成的∑S和小特征值组成的∑N。US为大特征值所对应的特征矢量所张成的信号子空间,UN则为噪声子空间。
在理想情况下,接收数据中的信号子空间与噪声子空间相互正交,所有信号子空间的导向矢量与噪声子空间正交,可以得到:
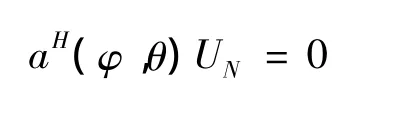
对协方差矩阵进行特征分解可得:
在实际中由于接收数据矩阵是有限长,所以用最大似然估计得到的噪声子空间特征矢量矩阵与a(θ)并不能完全正交,故算法以最小优化搜索实现[3,13]:

通过搜索式(7)的空间谱峰值,可得各个来波信号的波达方向角估计值(),这个估计值存在较大的误差,需进一步处理。

式(8)中w=[1 0 0… 0]T,式(9)中UN表示数据协方差矩阵RXX特征值分解的噪声子空间,即未经过校正的阵列接收数据协方差矩阵的特征分解值。对于存在幅相误差的阵列,导向矢量用误差估计值进行修正后信号子空间依然遵循与噪声子空间的正交关系。当待估计的波达方向角()和幅相误差估计矢量与真实值相符时,代价函数J取得最小值。因此可以通过对最小代价函数进行搜索,使其逼近最小值,就能得到波达方向角(φ,θ)和幅相误差估计值Г。
建立代价函数:
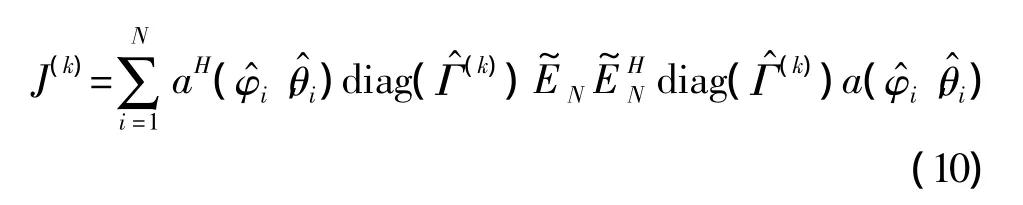
通过迭代法求解最终的估计值:


第四步判断式(10)代价函数J(k)是否收敛,若收敛则跳到第五步,否则k=k+1,跳到第二步,收敛条件为代价函数J(k+1)-J(k)≤T0,T0为门限值,也可以通过设置一定的迭代次数来停止迭代;
4 仿真实验
对本文提出的算法,进行计算机仿真实验。实验中,假设阵列为等距均匀圆阵,阵元数L=8,阵元间距为半波长,待估计信源为远场窄带信号,噪声为加性高斯白噪声,快拍数为512,幅度误差μ为原幅度值±0.2倍范围内的随机数,相位误差ϑ的范围为0~1.4rad。以下仿真实验均在同一硬件环境下运行。
实验一:阵列幅相误差对均匀线阵MUSIC算法的影响。
入射角度分别为(20°,20°),(60°,70°),(60°,80°),信噪比SNR=15dB。图2为无幅相误差的空间谱估计图,图3为有幅相误差的空间谱估计图,其中(a)空间谱估计的三维图,(b)为空间谱估计的俯瞰图。
通过图2和图3的比较可知,在没有幅相误差的情况下,MUSIC算法能够很好的估计出信源的波达方向,但是当存在幅相误差时,MUSIC算法的估计性能急剧下降,严重影响了波达方向的估计效果。
实验二:幅相误差自校正后的空间谱估计。
入射角度分别为(20°,20°),(60°,70°),(60°,80°),信噪比 SNR=15dB,迭代门限值 T0=0.01,算法经4次迭代后收敛。图4为幅相误差校正后的空间谱估计图,其中(a)空间谱估计的三维图,(b)为空间谱估计的俯瞰图,表1为幅相误差估计值与真实值对照表。

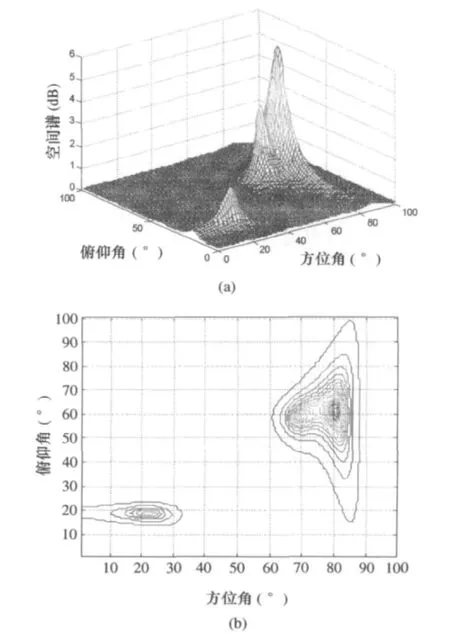
图4 经过幅相误差校正后的空间谱估计图

表1 幅相误差估计值与真实值对照表
从图4和表1可以看出,通过本文的自校正算法能够有效的校正幅相误差,可以得到较好的空间谱估计图和幅相误差估计值。
实验三:幅相误差校正算法的性能随信噪比变化的影响。
入射角度为(30°,60°),信噪比 SNR=0 ~20dB,迭代门限值T0=0.01,算法经4次迭代后收敛,角度估计值取100次Monte Carlo实验的平均值,分别计算校正前后俯仰角和方位角的估计值和真实值的均方根误差,定义均方根误差为:

图5表示了在幅相误差校正前后俯仰角和方位角随信噪比的变化。
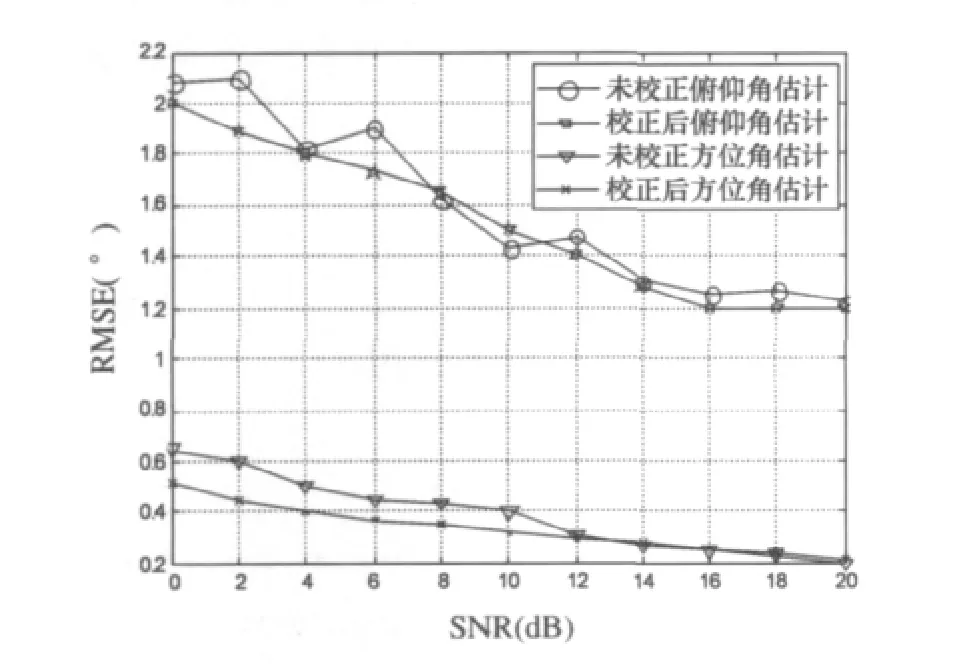
图5 幅相误差校正前后角度估计RMSE曲线
从图5可以看出,通过幅相误差校正后的角度估计误差小于校正前的角度估计误差。还可以看出,信噪比越大,算法的估计效果越好。
5 结束语
本文针对均匀圆阵中存在阵元幅相误差的问题,提出了基于MUSIC算法和迭代法的幅相误差自校正算法。先对均匀圆阵及其基础上的幅相误差建立数学模型,利用阵列接收数据协方差矩阵的结构特点,对波达方向角和幅相误差进行初步估计,根据初始估计值,再运用迭代的方法对波达方向和幅相误差值进行精确估计。仿真结果证明了本文提出算法的有效性。本文提出的算法对于解决空间谱估计的实际工程应用,具有重要意义。
[1]王永良,陈辉,彭应宁等.空间谱估计理论与算法[M].北京:清华大学出版社,2004.
[2]张贤达.现代信号处理[M].北京:清华大学出版社,2002.
[3]Liao B,Liao G S.Method for array gain and phase uncertainties calibration based on ISM and ESPRIT[J].Journal of Systems Engineering and Electronics(in Chinese),2009,20(2):223-228.
[4]Ferreol A,Larzabal P,Viberg M.On the resolution probability of MUSIC in presence of modeling errors[J].IEEE Transactions on Signal Processing,2008,56(5):1945 -1953.
[5]Min Lin,Luxi Yang.Blind calibration and DOA estimation with uniform circular arrays in the presence of mutual coupling[J].IEEE Antennas and Wireless Propagation Letters,2006,5:315 -318.
[6]Abed-Meraim K,Gazzah H.Optimum ambiguity free directional and omnidirectional planar antenna arrays for DOA estimation[J].IEEE Trans.on Signal Processing,2009,57(10):3942-3953.
[7]Sellone F,Serra A.A Novel online mutual coupling compensation algorithm for uniform and linear arrays[J].IEEE Trans.on SP,2007,55(2):560 -573.
[8]陈德莉.波达方向估计中阵列误差校正技术研究[D].国防科技大学博士论文,2008,30-40.
[9]杨璋.波达方向估计中阵列幅相误差校正技术研究[D].成都:西南交通大学,2010.
[10]苏卫民,顾红,倪晋麟等.多通道幅相误差对空域谱及分辨性能影响的分析[J].电子学报,2000,28(6):30 -35.
[11]Wang B H,Wang Y L,Chen H.Array calibration of angularly dependent gain and phase uncertainties with instrumental sensors[C].IEEE International Symposium on Phased Array Systems and Technology,Boston,Massachusetts,USA,2003,182 -186.
[12]Li Qiong,Ye Zhongfu.DOA and Doppler frequency estimation with sensor gain and phase uncertainties[J].Neural Networks and Signal Processing,Dec.2003,2:1314 -1317.

