机载火控雷达功率非均匀杂波抑制研究

李静静 罗丁利

(西安电子工程研究所 西安 710100)

1 引言

由于实际地貌的非均匀性，机载雷达在下视工作时常常面临非均匀场景[1，2]。功率非均匀是指杂波功率随距离产生的剧烈变化，主要由杂波干扰引入，如不同地貌交界处、高大物体及其遮蔽、人造孤立强杂波点等都会产生功率非均匀现象。功率非均匀会导致对杂波功率估计不准，影响样本协方差矩阵估计和相应自适应权值的计算[3]。

为了降低功率非均匀对自适应算法的影响，文献[4]提出了一种协方差矩阵加权的算法，它能部分地改善功率非均匀带来的问题，但不能加深凹口，对强杂波的抑制依旧不足。后来学者们相继提出了一些基于训练样本选取的算法，大致可分为数据独立的方法、数据相关的方法两类。数据独立的方法主要包括局域法和超零陷法。局域法假设数据是“局域均匀”的，选择检测单元邻近的距离单元作为训练样本进行自适应处理，常见的修正的采样协方差矩阵求逆法(MSMI)[5]就基于此种思想。超零陷法是通过雷达距离方程选择强杂波区的样本进行自适应处理，虽然能解决强杂波点(又称分立杂波)的问题，但是算法性能受地形因素影响较大。文献[2]提出的功率选择训练法(PST)和功率选择削弱法(PSD)则是基于数据相关的思想，由于利用了回波数据之间的相关信息，很好地解决了功率非均匀的问题。

本文从样本选取的角度，着重对修正的采样协方差矩阵求逆法、功率选择训练法和功率选择削弱法进行对比研究，并通过对实测数据的处理验证各算法的性能。

2 样本选取策略

在非均匀环境下，样本选取方法(也称样本选取策略)直接影响着自适应杂波抑制算法的性能。样本选取策略的最终目标是获得待检测单元中干扰协方差矩阵的最佳估计，它需要考虑两个方面的问题:一是如何选取样本使其统计特性与待检测单元相同，二是选择多少个样本可以获得协方差矩阵的最佳估计。

2.1 修正的采样协方差矩阵求逆算法

修正的采样协方差矩阵求逆(MSMI)算法假设杂波是局域均匀的，在待检测单元周围设置一定数目保护单元，然后从剔除保护单元后的邻近单元中选取样本进行协方差矩阵估计和自适应权值计算[6]。

对于某一多普勒通道，设xn为检测单元，在检测单元两侧各设置l个保护单元，然后在保护单元两侧各选取N个单元(称为参考单元)，那么修正的协方差矩阵x为:

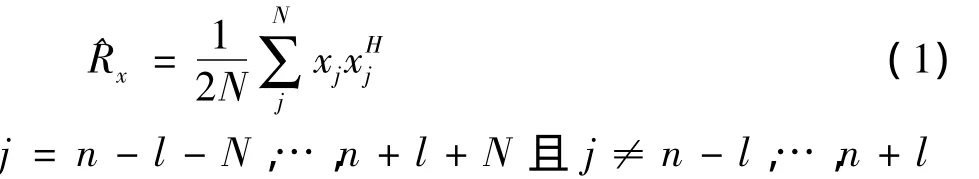
由于MSMI是基于杂波数据“局域均匀”的假设，因而在进行样本选取时，参考单元的样本数据应该是均匀或近似均匀的。若系统自适应的自由度为Q，则参考单元的数量一般为2Q～10Q[2]。保护单元的设置应当考虑雷达的距离分辨率，保证检测单元中的目标及旁瓣能量不能同时出现在参考单元里，以免污染参与协方差矩阵估计的样本数据。

2.2 功率选择训练法

功率选择训练法(PST)假设杂波的非均匀主要体现在沿距离向的功率变化上，通过选取一系列快拍中强功率样本集来进行协方差矩阵估计和自适应权值计算，以抑制样本中的强杂波，它在训练样本充足时能很好地解决功率非均匀问题。文献[2]中提到了它的处理过程，具体步骤如下:

a.对于每一个多普勒通道，估计对应的锥角φ，并计算指向该通道的目标导向矢量vc;

b.计算滤除干扰的权值vw=vc，为无杂波干扰(即目标和噪声)协方差矩阵;

d.排序y'=sort(y)，选取一定数目的强杂波样本作为训练样本进行协方差矩阵估计。

2.3 功率选择削弱法

功率选择削弱法(PSD)是在自适应滤波前首先识别出快拍数据中的分立杂波，然后采用训练样本中检测单元的一部分来修正协方差矩阵，从而实现对分立杂波的抑制，降低了目标的自相消效应。PSD修正的协方差矩阵为:

其中~K－1=K+γ，γ是衰减因子，在0到1之间取值[2]:当γ=0时，表明检测单元不参与协方差矩阵估计;当γ=1时，表明检测单元完全参与协方差矩阵估计;当0＜γ＜1时，表明检测单元的一部分参与到协方差矩阵估计中。γ的选取到目前为止还没有一个最优的准则，一般是基于幅度统计量，比如将期望的杂波功率降至一定水平(如0dB)等[2]。

2.4 性能对比分析

MSMI选取的是检测单元邻近的距离单元作为训练样本，构建的协方差矩阵在一定程度上能够准确反映检测单元的杂波特性。此外，MSMI设置了保护单元，由于保护单元是不参与协方差矩阵估计的，当分立杂波和干扰目标进入保护单元时，它们的影响就大为减弱了，因而保护单元的设置在一定程度上能够提高MSMI对分立杂波和干扰目标的抑制效果。但无论如何选取样本，MSMI对分立杂波和干扰目标的抑制性能都不会很好，因为在检测到某些单元时，分立杂波和干扰目标总有机会进入参考单元，从而造成协方差矩阵估计不准确。

与MSMI不同，PST选取强功率样本进行协方差矩阵估计和自适应权值计算，形成足够深的凹口来抑制分立杂波，降低杂波剩余功率，从而有效地改善杂波对消效果，提高输出信杂噪比，有利于动目标的检测和分立杂波的抑制。然而当场景中存在超强杂波时，即使采用强功率样本进行自适应处理也难以形成超深凹口将其抑制，因此PST对超强杂波的抑制性能是非常有限的。而PSD对超强杂波有很好的抑制效果，这是因为当超强杂波位于检测单元时，PSD采用超强杂波的一部分来修正协方差矩阵，加深了自适应方向图的凹口，从而降低了超强杂波的剩余功率，实现对它的抑制。但是在分立杂波较多的场景中，若单一使用PSD运算量会非常大，因此在实际处理中，通常将PSD和PST两种算法结合起来使用。

在下节的实测数据仿真分析中将从自适应滤波输出、改善因子、虚警率等角度对 MSMI和PST+PSD的性能进行进一步的分析对比。

3 实测数据分析

本文采用某机载火控雷达和差波束实测数据，选取了其中非均匀现象较明显的一段数据。其中和差通道数据如图1、图2所示，共512个多普勒通道、501个距离门，并人为在第275个多普勒通道第400个距离门处注入一个位于波束中心的弱目标，信杂比为2dB。

首先对MSMI和PST+PSD的训练样本选取数量问题进行研究分析。图3、图4分别为MSMI和PST+PSD算法在相同检测门限下虚警率随训练样本数目变化的统计结果。

从两幅图中可以看出，在一定范围内，两种算法的虚警率都随着训练样本的增加而减小，这是因为用少量的训练样本估计出的协方差矩阵与检测单元的真实协方差矩阵失配较大，随着样本数目的增加，估计的协方差矩阵与检测单元的真实协方差矩阵的匹配度越来越好，而当训练样本增加到一定数量的时候，虚警率会逐渐趋于稳定。鉴于自适应算法的运算量正比于样本数目的平方，因此选取的训练样本数量也不宜过多。根据两幅图的统计结果，在下面的自适应处理中，MSMI选取16个样本，PST+PSD选取250个样本。

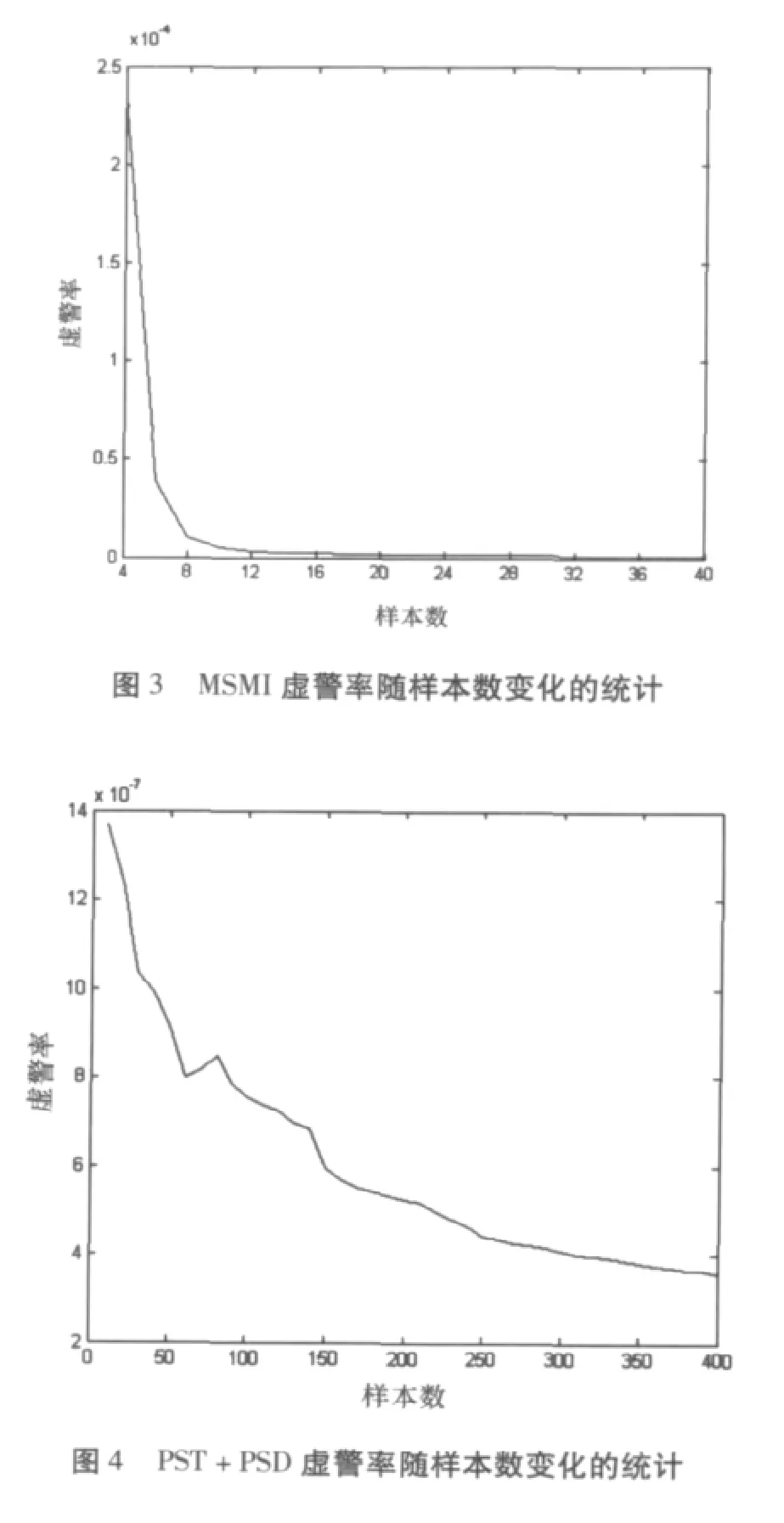
然后对MSMI和PST+PSD的自适应滤波输出结果进行对比分析。图5、图6分别为MSMI和PST+PSD算法的自适应滤波输出结果。

观察这两幅图可以看出:在主瓣杂波区，MSMI剩余杂波功率沿距离变化很显著，尤其是原始数据中几个分立杂波处剩余杂波功率依然很高;而PST+PSD剩余杂波功率相对MSMI来说要平稳的多，且分立杂波的剩余功率较MSMI低了许多，这在一定程度上都会降低虚警率，从而有利于动目标的检测。对自适应滤波输出结果进行分析计算的结果显示:在主瓣杂波区，MSMI和PST+PSD的剩余杂波平均功率相当，均为110.5dB，而在几个分立杂波处PST+PSD明显优于MSMI;在清洁区，MISMI的剩余杂波平均功率是 102.5dB，而 PST+PSD为101.9dB，整体降低了约0.6dB。

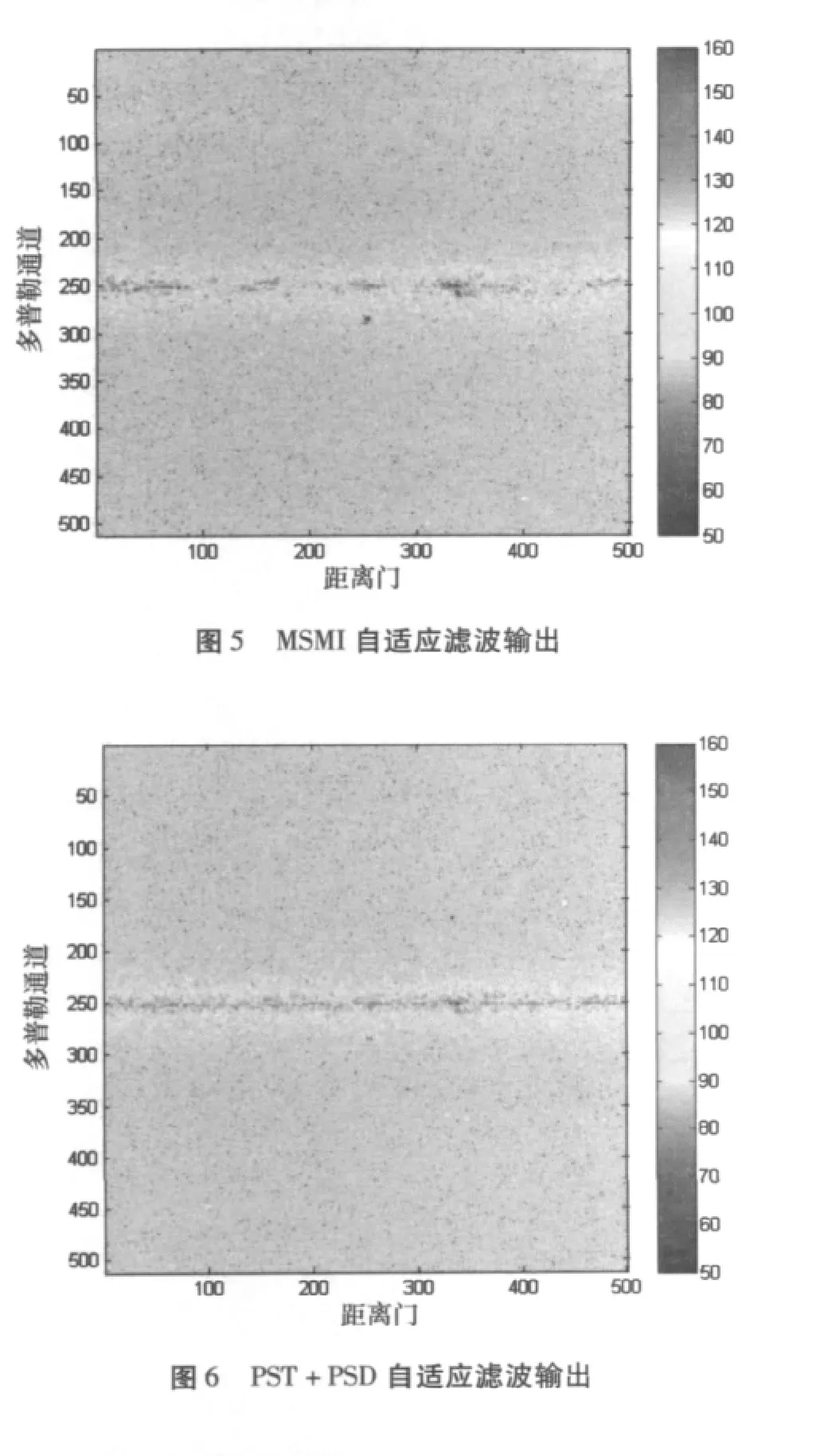
接着比较MSMI和PST+PSD处理后的目标所在多普勒通道的剩余杂波功率。图7为自适应滤波前第275个多普勒通道的数据，用虚线圆圈标注了弱目标的位置。图8为第275个多普勒通道归一化剩余杂波输出功率，同样用虚线圆圈标注了弱目标的位置，其中MSMI和PST+PSD功率峰值点均为目标点。从图中可以看出，MSMI的归一化剩余杂波功率普遍高于PST+PSD，对照图7可见，MSMI几个分立杂波处的剩余功率依然很高，相较之下PST+PSD要好得多。此外，对该通道归一化剩余杂波平均功率进行计算的数据显示:MSMI为－14.6dB，而PST+PSD为－15.4dB，降低了0.8dB。

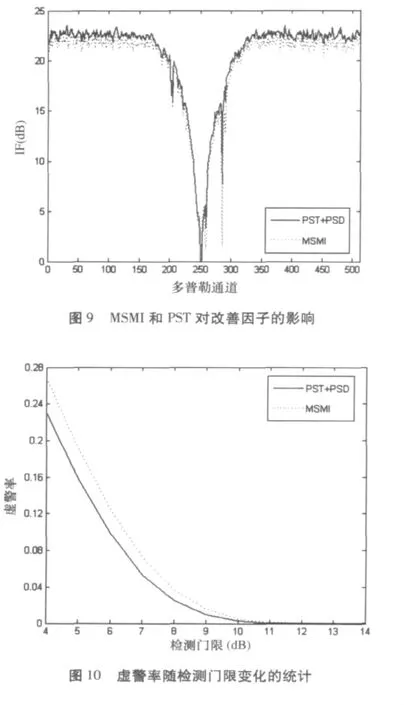
最后从改善因子和虚警率的角度比较MSMI和PST+PSD的性能。图9为MSMI和PST+PSD对改善因子的影响。如图所示，对于大多数多普勒通道来说，二者的改善因子相差不大，但当存在超强分立杂波时二者的差别就非常明显了，比如第258个多普勒通道，PST+PSD的改善因子比MSMI提高了大约1.1dB，第285个多普勒通道，PST+PSD的改善因子比MSMI提高了大约7.1dB。图10为MSMI和PST+PSD虚警率随检测门限变化的统计结果。如图所示，两种算法的虚警率都随着检测门限的提高而降低，但在相同检测门限下，MSMI的虚警率要比PST+PSD高，这说明PST+PSD在降低虚警率方面确实优于MSMI。

4 结论

为了抑制功率非均匀现象，本文从样本选取的角度分别对修正的采样协方差矩阵求逆算法、功率选择训练法和功率选择削弱法进行了分析研究，分别用上述算法对某机载火控雷达实测数据进行了处理，讨论了实测数据中样本选取数量的问题，并从剩余杂波功率、改善因子和虚警率等角度分析了算法性能的优劣。研究结果显示，在功率非均匀背景下，功率选择训练法和功率选择削弱法在抑制杂波尤其是分立杂波、提高输出信杂噪比、降低虚警率方面都要优于修正的采样协方差矩阵求逆算法，它能够有效地减少虚警，提高对弱目标的检测能力，加之工程实用性较强，非常适用于分立杂波较多的场景。

[1]Rabideau D.J，Steinhardt A.O.Improving the performance of adaptive arrays in nonstationary environments through data－adaptive training[C].Proc.of the 30th Asilomar Conf.on Signals，Systems and Computers，Pacific Grove，CA，USA，Nov.1996:75～79.

[2]Rabideau D.J，Steinhardt A.O.Improved adaptive clutter cancellation through data－adaptive training[J].IEEE Trans.on AES，1999，35(3):879～891.

[3]谢文冲，王永良.非均匀杂波环境STAP方法研究[J].自然科学进展，2007，4(17):513～519.

[4]Guerci J.R.Space-time adaptive processing for radar[M]. Boston， London: Artech House，2003.

[5]Wichs M.C，Melvin W.L，Chen P.An efficient architecture for nonhomogeneity detection in space－time adaptive processing airborne early warning radar[C].Radar1997，1997:295 ～299.

[6]王彤，保铮.空时二维自适应处理的目标污染样本挑选方法[J].电子学报，2001，29(12A):1840～1844.