基于复杂网络的循环经济系统产业链分析

吕 敏，宋华岭

(1.山东师范大学 管理科学与工程学院，济南250318;2.山东工商学院管理科学与工程学院，山东烟台264005)

循环经济是人类为实现可持续发展而采用的旨在保护环境、维持生态平衡，将传统的开环经济形式转变为闭环流动的经济形式，摒弃了传统的“资源—产品—废弃物”单项直线式经济发展模式，采用了“资源—产品—废弃物—再生资源”的反馈式循环经济发展模式，从而能真正的实现煤炭资源利用的低消耗、低排放和高效率，并能以尽可能少的环境成本和资源消耗获得尽可能多的经济效益和社会效益。循环经济是以协调人与自然关系为基准，模拟生态系统运行方式和规律，实现资源的可持续利用，并使得社会生产从数量型的物质增长转型为质量型的服务增长。而且，循环经济还延伸了产业链，推动其他产业的发展，从而促进了国家的社会发展和经济增长。

循环经济方面，很多研究者分别将循环经济的理论应用于合成革产业、有色金属产业、土地资源、固体废物治理、钢铁工业、镁砂企业［1－6］。产业链方面，李巍等提出从循环经济的角度来构建煤炭产业的产业链，促进煤炭资源的高效利用，实现良性循环，保护煤炭资源，这是煤炭经济可持续发展的合理有效途径［7］。赵淑英等人在分析煤炭循环经济产业链优势的基础上，从纵向主导产业链和横向耦合产业链等方面，构建出我国煤炭循环经济产业链发展模式［8］。

复杂网络的理论研究始于1960年，由著名数学家Erdos和Renyi提出的ER随机图模型展开。自从1988年Watts和Strogatz发表在Nature上的小世界网络及一年后Albert和Barabasi在Science上发表的无标度网络以来，研究者们开始了由研究简单规则网络转为研究复杂网络，复杂网络作为大量真实复杂系统的高度抽象，近年来引起了研究者们的广泛研究。目前研究复杂网络主要是研究网络的以下几个方面:几何性质、形成机制、演化的统计规律、模型性质、结构稳定性和演化动力学机制。

目前国内对复杂网络理论的研究现状是:汪小帆在2002年在国外杂志上发表了一篇文章，文章回顾了近年来国外复杂网络研究所取得的重要成果［9］。赵月等人详细分析了城市交通网络的特性，并从网络实证、演化机制、演化性质、动力学和结构稳定性5个方面总结了复杂网络理论在城市交通网络分析中的研究进展，指出了目前存在的问题，最后给出了城市交通网络复杂性研究的几个可能方向［10］。徐娟认为物流系统是开放的复杂网络系统，并基于物流网络本身的特性，利用复杂网络理论对物流网络度分布进行理论分析，最后验证了物流网络度分布的稳定性［11］。武鹏飞等以北京西北部的官厅水库流域为研究区，应用度、介数、网络平均最短路径等复杂网络方法，从土地利用系统整体的角度识别LUCC过程中关键变化的地类，评价土地利用系统的稳定性，分析生态环境变迁［12］。

一、循环经济系统产业链的复杂网络评价模型建立

本文从3个方面对循环经济系统产业链的复杂网络进行分析，分别是:平均路径长度、聚类系数、度及度分布。复杂网络的几个重要的统计特征描述如下:

1.平均路径长度

网络中连接节点i和j的最短路径上的边数定义为两节点间的距离dij;网络中任意两节点间的距离的最大值定义为网络的直径;任意两个节点之间距离的平均值定义为网络的平均路径长度l，其中N为网络节点数，则平均路径可表示为

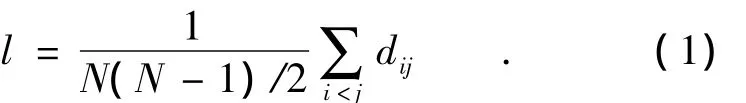
显然，平均路径决定了系统的顺畅程度，这在流的决策中，尤其是信息流的决策中，具有很强的实际意义。这个参数越小，表明该网络越小，结构越紧凑，到达目标位置的时间越短、失真性越小。同理，此参数越大，表明该结构越大，结构越松散，到达目标位置的时间越长，失真性越大。

2.聚类系数

若网络中存在一节点i，它周围有ki条边将其与其他节点相连接，则这ki条边另一端所连的ki个节点称为节点i的邻居，邻居节点可能相互连线数为ki(ki－1)/2，而实际连线数为Ei。则实际连线数Ei和邻居节点可能相互连线数ki(ki－1)/2之比定义为节点i的聚类系数Ci，即

从几何特点看，上式的一个等价定义为

整个网络的聚类系数就是所有节点的聚类系数的平均值，从另一方面也反映出网络中三角形的密度程度。聚类系数表示了系统中每个节点的周边节点之间的连接程度，也表示了这一节点的次级吸引力。显然，聚类系数越高，表示该网络的密度越大，系统的稳定性越高。同理可得，聚类系数越低，表示该网络的的密度越小，系统的稳定性越低。

3.度与度分布

网络中节点i的度定义为与节点i相连接的其他节点的数目，度是单独节点的属性中简单而又非常重要的概念，一个节点的度越大表示在某种意义上该节点在网络中越关键。网络的平均度定义为网络中所有节点的度的平均值。本文用分布函数p(k)来表示网络中节点的度分布，函数定义为随机选定的节点的度正好为k的概率。

网络的度分布显示出了网络内每个节点与其他节点连接数目的分布规律，是网络结构中一个很重要的几何特征。

二、具有代表性的复杂网络模型

1.规则网络模型

本文主要介绍3种规则网络模型:

全局耦合网络指的是网络中任意两点之间都是连通的。由前面介绍的平均路径长度和聚类系数的计算方法可得全局耦合网络的平均路径长度是1，其聚类系数也是1。虽然很多实际网络具有的性质可以由全局耦合网络模型来反映，但是该网络模型也有其局限性，由N个点构成的的全局耦合网络共有N(N－1)/2条边，大多数的实际网络都是稀疏的，其边数达不到如此之多。

最近邻耦合网络是指一个稀疏的规则网络模型，它的每一个节点只和该节点周围的2K个邻居节点相连。由N个节点构成的最近邻耦合网络中，围成一个环的点的个数为N，其每个节点都与它各自左右的K个邻居节点相连接。对于较大的K值，最近邻耦合网络的聚类系数为

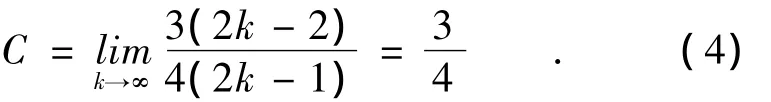
所以，此网络的聚类系数是很高的。对于给定的K值，网络的平均路径长度为

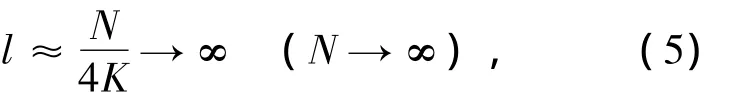
由此说明最近邻耦合网络不是小世界网络模型。

星形耦合网络是指网络中有一个中心点，其余所有的节点都只与这个中心点有边相连，而它们彼此之间没有边相连接。若某星形耦合网络有N个节点构成，则其平均路径长度为

聚类系数为

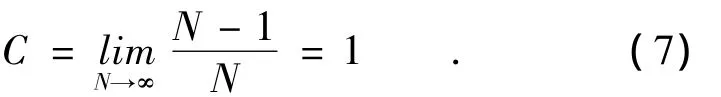
2.ER随机网络模型

ER随机网模型的最简单表述为:(1)给定网络节点总数N;(2)在每一步时间，任意选择2个节点，以概率把它们连边，其中n是)给定的总边数，n小于N(N－1)/2，N(N－1)/2是最大可能连边数;(3)当边数达到n时停止演化。

3.小世界网络模型

在现实生活中，大多数的真实网络具有小的平均路径长度和相对较大的聚类系数。由规则网络到完全随机网络的过渡，在1998年 Watts和Strogtz提出了小世界网络模型，也就是下面要提到的WS小世界模型。

用人际关系网作为小世界网络模型的案例。大部分的人际关系可能都是近距离的，例如家属关系、同学关系等，类似于规则网模型中的邻边;很多人也有远方的人际关系，例如移居在国外的亲戚朋友等，类似于ER随机网络模型中的远程跳跃边。小世界网络模型的度分布可近似表示为泊松分布，该分布的特点是在度平均值处有一个峰值，紧接着呈指数快速衰减。

4.无标度网络模型

近年很多的复杂网络研究表明，许多复杂网络的度分布不同于泊松分布，幂律分布可以更好地表示它们的度分布。因为此类网络节点的连接度没有明显的特征长度，所以称为无标度网络。幂律分布与泊松分布的最大不同是前者比后者的曲线下降要缓慢些，幂律分布也称为无标度分布。

无标度网络模型由Barabasi和Albert提出，他们认识到实际网络存在2个重要特性:(1)增长特性，即网络规模是不断扩大的。(2)优先连接特性，即新的节点倾向与那些具有较高连接度的“大”节点相连接，这也就是人们所认识到的“富者更富”现象。

5.局域世界网络模型

研究者在对世界贸易网的研究中发现，由于常常缺乏全局信息，BA模型建议的全局优选连接机制通常只能在从事选择节点的某个或某些局域世界中起作用。在这个贸易网中，每个节点代表一个国家，两国家之间有贸易关系，则相应的2个节点之间有连接边。容易理解，许多国家都致力于加强与各自的区域经济合作组织之内国家之间的经济合作和贸易关系，在这些区域经济合作组织中，才优先考虑与那些最强大的国家多进行贸易合作，而在这些区域经济合作组织之外与许多国家很少有贸易往来，也就谈不上选择了。可见优先连接机制是存在于某些区域经济体中的，说明了复杂网络中存在着局域世界，由此李翔和陈关荣提出了局域世界网络模型。现实生活的许多网络中，由于存在着局域世界连接性，每个节点有着各自的局域小世界，所以它们只使用和占有整个网络的局部连接信息。

6.赋权演化网络的BBV模型

以上介绍的网络都是无权网，在现实生活中的网络大多数为有权网，所以巴黎特、巴斯莱米与维斯匹纳尼建立了赋权演化网络的BBV模型。该模型基于一个简单的权重驱动动力学假设，生成了与真实权重网络极为相似的统计性质，如网络权重随时间的增长演化规律及强度分布的无标度性等。

模型可简述如下:从初始的N0个相互连接的种子节点开始网络生长，此时每条边的权重为w0，然后每步增加一个节点直到节点数为N;每步增加的节点发出m条边，以如下的概率按照点强度优选连接到已有的节点i，这个规则放弃了通常的度优选连接，而改用强度优选连接。

三、实证研究:典型煤炭行业循环经济系统产业链的复杂网络评价

依据上述模型，分别对西山煤电集团古交循环经济园区和同煤塔山循环经济园区的产业链进行了复杂网络分析及评价，产业链的结构如图1、图2所示;由于信息传递是相互的，所以拓扑结构图为无向的，则网络拓扑结构图分别如图3、图4所示。

对两个循环经济园区运用上述模型进行计算，计算得出古交循环经济园区产业链和同煤塔山循环经济园区产业链的平均路径长度分别为3.02和1.92;平均度分别为2和20/9;网络的聚类系数分别为0和7/45，其他指标计算结果如表1、表2、表3、表4所示，用Matlab软件画出各自的网络度分布图分别如图5、图6所示。其中，图3中1～20分别代表古交循环经济园区的古交煤矿、氧化供热、煤气压缩站、古交选煤厂、瓦斯电厂、焦化厂、铁路、煤矸石制砖厂、古交配煤厂、铁厂、化肥厂、电石厂、煤焦油深加工厂、古交电厂、PVC厂、电石渣水泥厂、氧化铝厂、陶粒厂、砖厂和硅钙渣水泥厂。图4中1～9分别代表塔山循环经济园区的塔山矿井、坑口电厂、选煤厂、甲醇厂、综合利用电厂、铁路、高岭岩深加工厂、煤矸石烧结砖厂和新型干法水泥厂(表1中的i代表图3中的节点1～20，表2中的i代表图4中的节点1～9)。

图1 古交循环经济产业链的结构图

表1 古交循环经济产业链网络的各点的聚类系数表

四、结论

由上述数据表明，古交循环经济园区产业链网络的平均路径长度大于塔山循环经济园区，从而说明塔山循环经济园区的网络小，结构紧凑。由网络结构图也可以看出塔山循环经济园区的规模比古交循环经济园区的小。

古交循环经济园区产业链网络的聚类系数为0，而塔山循环经济园区的聚类系数为7/45，说明塔山循环经济园区的密度高、稳定性高。

由表1和表2可得出:古交循环经济园区产业链中古交选煤厂、焦化厂和古交电厂在产业链中比较重要，因为它们的度都为5，是产业链中度最大的;塔山循环经济园区产业链中选煤厂比较重要，其度数为6，是产业链中最大的。

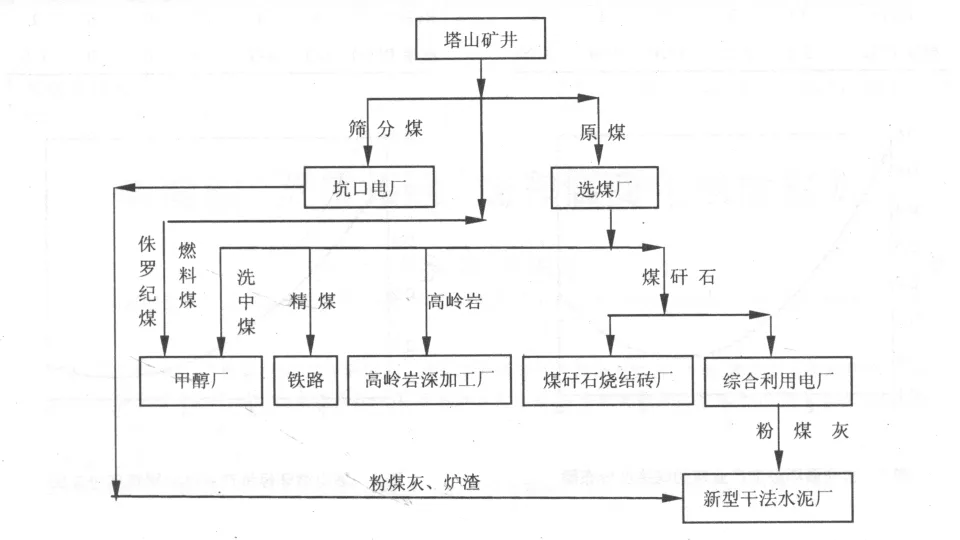
图2 塔山循环经济园区产业链的结构图

图3 古交循环经济产业链的网络拓扑结构

图4 塔山循环经济产业链的网络拓扑结构

表2 塔山循环经济产业链网络的各点的聚类系数表

由网络度分布图5、图6可得出:两者的分布图图形类似，都属于幂律分布。从图形可看出:网络中大多数的节点拥有少量的连接，少部分的节点拥有大量的连接，也就证明了古交循环经济园区和塔山循环经济园区的产业链网络属于无标度网络。

表3 古交循环经济产业链的网络度分布值表

表4 塔山循环经济产业链的网络度分布值表

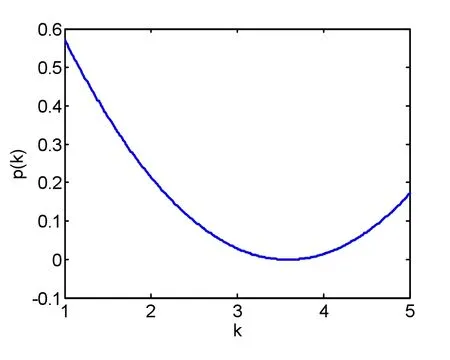
图5 古交循环经济产业链的网络度分布图

图6 塔山循环经济产业链的网络度分布图

［1］黄朝阳.循环经济与温州合成革产业的可持续发展［J］.环境保护与循环经济，2009，(4):18－20.

［2］张晓缝.发展有色金属工业循环经济初探［J］.环境保护与循环经济，2009，(6):19－20.

［3］陈文瑞.循环经济下的土地资源可持续利用［J］.改革与开放，2009，(9):60.

［4］刁小冬，周凯慧.浅析循环经济在固体废物治理中的应用［J］.环境保护与循环经济，2011，(1):37－39.

［5］常艳君.钢铁工业发展循环经济的效益分析［J］.环境保护与循环经济，2011，(1):40－41.

［6］赵峰.镁砂企业发展循环经济探析——以中兴矿业为例［J］.环境保护与循环经济，2011，(7):35－37.

［7］李巍，罗能生.基于循环经济的煤炭产业链建构［J］.煤炭经济研究，2006，(11):19－21.

［8］赵淑英，王鑫.我国煤炭循环经济产业链发展模式研究［J］.中国矿业，2009，18(3):52－55.

［9］WangXiaofan.Complex networks:topology，dynamics and synchronization［J］.International Journal of Bifurcation and chaos，2002，12(5):885 －916.

［10］赵月，杜文，陈爽.复杂网络理论在城市交通网络分析中的应用［J］.城市交通，2009，7(1):57－65.

［11］徐娟.基于复杂网络的物流网络度分布［J］.物流技术，2011，(6):89－91.

［12］武鹏飞，宫辉力，周德民.基于复杂网络的官厅水库流域土地利用/覆被变化［J］.地理学报，2012，67(1):113－121.