基于Burg法AR模型谱估计的涡街流量计旋涡脱落频率提取

孙志强 ，陈延平

(1. 中南大学 能源科学与工程学院，湖南 长沙，410083；2. 中南大学 流程工业节能湖南省重点实验室，湖南 长沙，410083)

在能源、动力、石油、化工等流程工业中，流量是与生产效率和操作安全密切相关的最为重要的过程参数之一。作为一类精度较高的通用流量仪表[1]，涡街流量计近年来得到了迅速发展[2]，已被广泛应用于液体、气体、蒸汽和部分混相流的测量[3-4]。涡街流量计的原理是利用垂直插入流体中的非流线型旋涡发生体产生旋涡脱落形成卡门涡街，当满足一定雷诺数条件时，旋涡脱落频率与流速成正比，此时采用适当的检测技术获取频率，即可实现流量测量。在实际使用过程中，涡街流量计不可避免地会受到与之相连接的管道和设备振动的影响，致使其输出信号中含有大量噪声，严重时甚至导致信号完全失真[5]。如何从含有噪声的信号中准确提取出旋涡脱落频率，日益成为优化和改进涡街流量计测量性能的核心问题之一[6]。综合实际可行性与应用成本，近年来数字信号处理方法被广泛应用于涡街流量计信号的去噪和旋涡脱落频率的估计[7]。Amadi等[8]在对原始测量信号进行谱估计的基础上，建立了涡街流量计信号表达式。Hondoh等[9]利用频谱估计技术对涡街流量计输出信号进行滤噪，以提高其测量精度。Xu等[10]通过嵌入功率谱分析技术，开发了具有实用价值的涡街流量计信号处理系统。孙志强等通过对管道内涡街流动稳定性[11]和流场结构[12]的分析，利用Hilbert-Huang变换对涡街流量计信号进行去噪[13]，探讨了涡街流量计信号的高阶统计量特征[14]、功率谱式表征[15]与测量介质类型和流量的关系。这些研究为涡街流量计旋涡脱落频率的准确提取奠定了基础。然而，各种信号处理方法由于受到本身理论的限制，只有在特定参数条件下才能得到满意的频率提取结果，其通用性尚待验证与提高。因此，寻找适合于涡街流量计信号分析的方法，研究其性能参数的优化设置，对旋涡脱落频率的准确提取与涡街流量计测量精度的提高都具有重要意义。

1 基于Burg算法的AR模型谱估计

现代谱估计以随机过程的参数模型为基础，能够基于有限数据从频域内提取出淹没在噪声中的有用信号。AR模型(自回归模型)谱估计是最为常用的一种用于信号特征分析的谱分析方法，其模型参数的精确估计只需求解一组线性方程即可获得。Burg算法是建立在数据基础上的AR模型系数求解的有效算法，已在通信滤波、图像处理等领域得到成功应用[16]。AR模型的Burg算法递推过程建立在数据序列基础上，避开了序列的自相关函数估计，所以，与自相关法相比，具有较好的频率分辨率[17]。

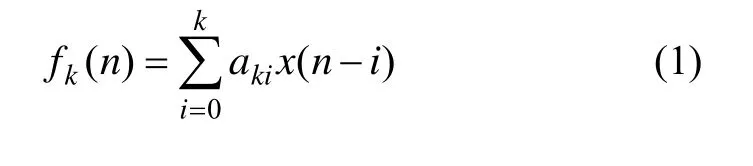
利用格型滤波器结构，计算各阶前向和后向预测误差为：

式中：λk为格型滤波器的反射系数。

前向和后向预测误差的平均功率为：

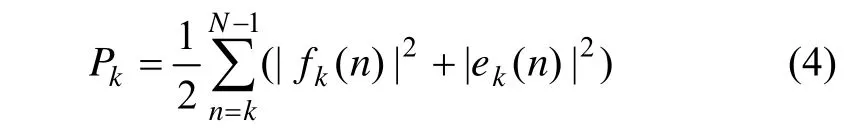
为使Pk最小，令∂Pk/∂λk=0，得到反射系数为：

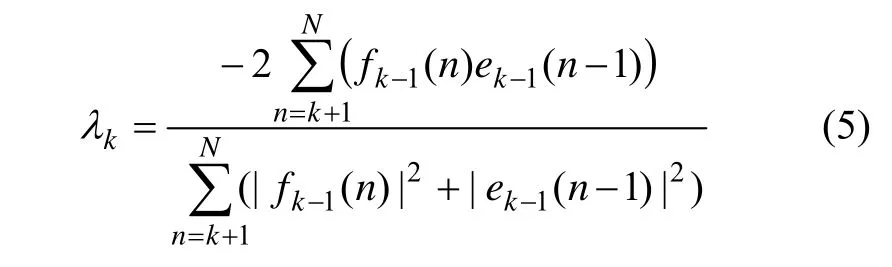
然后利用Levinson递推公式求出AR模型的参数为：

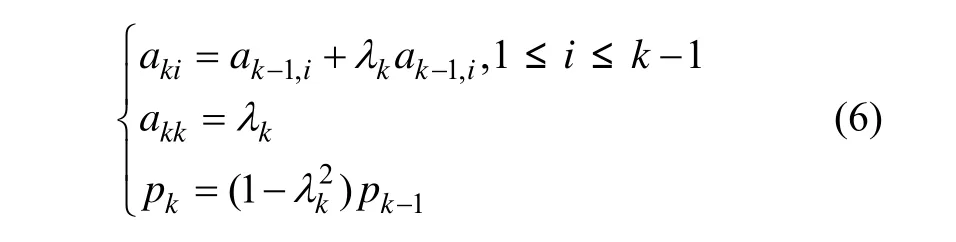
在Burg算法中，阶次直接关系到AR模型谱估计的质量。阶次过低，谱峰难以出现；阶次过高，可能产生虚假峰值。因此，阶次的合理选择是Burg算法能否准确提取涡街流量计旋涡脱落频率的关键。

2 实验

实验在自行搭建的实验台上进行。实验系统通过管道将蓄水池、水泵、稳压水罐、电磁流量计、涡街流量计连接成闭合回路，如图1所示。测量介质为室温下的水，首先由水泵将其从蓄水池中抽入稳压水罐中，经消除流动振荡后，依次流过提供参考流量读数的电磁流量计(精度为0.5级)和实验用涡街流量计，最后又流回蓄水池循环使用。实验的水流量范围为3～35 m3/h，其大小通过管路中的手动阀进行调节。

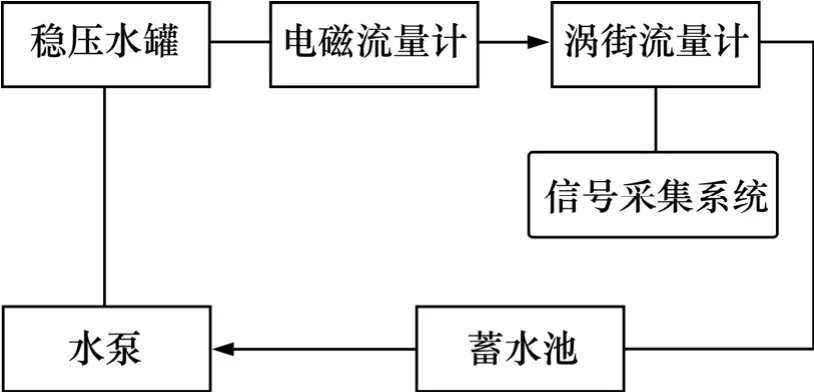
图1 实验系统Fig.1 Experimental system

实验用涡街流量计的仪表系数为9 217.08 m-3，测量管内径为50 mm，旋涡发生体为三角形柱体，迎流面宽度为14 mm。涡街流量计的旋涡脱落信号通过轴向管壁差压法[20]获取，上游和下游的取压孔分别位于旋涡发生体迎流面之前50 mm和之后10 mm。采用的差压传感器的动态响应时间为1 ms，其输出的电压信号经放大后由 Tektronix TDS3054B示波器采集和存储，采样频率设置为1 kHz，每次测量的采样时间为10 s。

总之，在概念教学中，教学方法有许多，合情推理作为促进学生概念学习的有效途径之一，教师应把握好课堂教学的时机，找准合情推理的方法，从而使概念学习过程更容易被学生理解与接受，进而全面提升概念教学质量。

图2所示为流量为11 m3/h时原始的涡街流量计输出信号片段。图 2(a)所示为流动平稳且无管道振动时的管壁差压信号，可以看到管壁差压做频率恒定的正弦波动，信号幅度变化较小，反映了涡街流量计内形成了规则的卡门涡街。图2(b)所示为来流振荡时的管壁差压信号，此时管壁差压整体上出现低频波动，信号幅度差异显著，表明涡街流量计中虽然存在旋涡脱落，但其稳定性受到影响，必须对原始信号进行适当处理方能有效提取旋涡脱落频率。

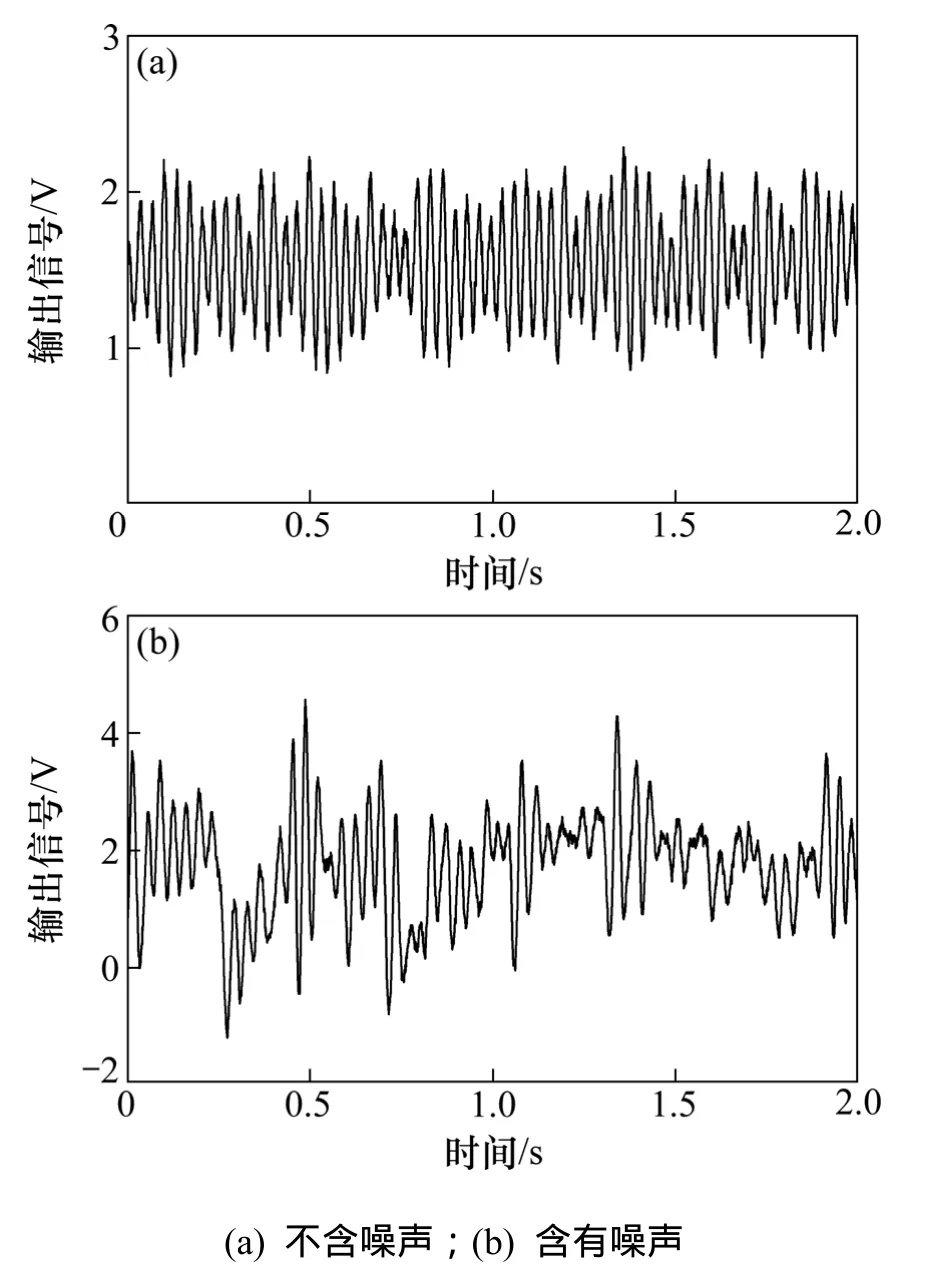
图2 涡街流量计输出信号Fig.2 Output signals of vortex flowmeter

3 结果与分析

对水流量为3～35 m3/h范围内的19组涡街流量计输出信号，采用基于Burg算法的100阶AR模型进行谱估计，提取的旋涡脱落频率结果如表1所示。其中，参考频率通过涡街流量计仪表系数计算得到，相对误差的计算以参考频率作为基准。从表1可知：基于Burg算法的AR模型谱估计对于不同流量下的涡街流量计输出信号都能准确提取出其中旋涡脱落频率。除了在个别流量(12.94 m3/h)下相对误差稍大外，其余流量下旋涡脱落估计频率的相对误差均在±3%以内。

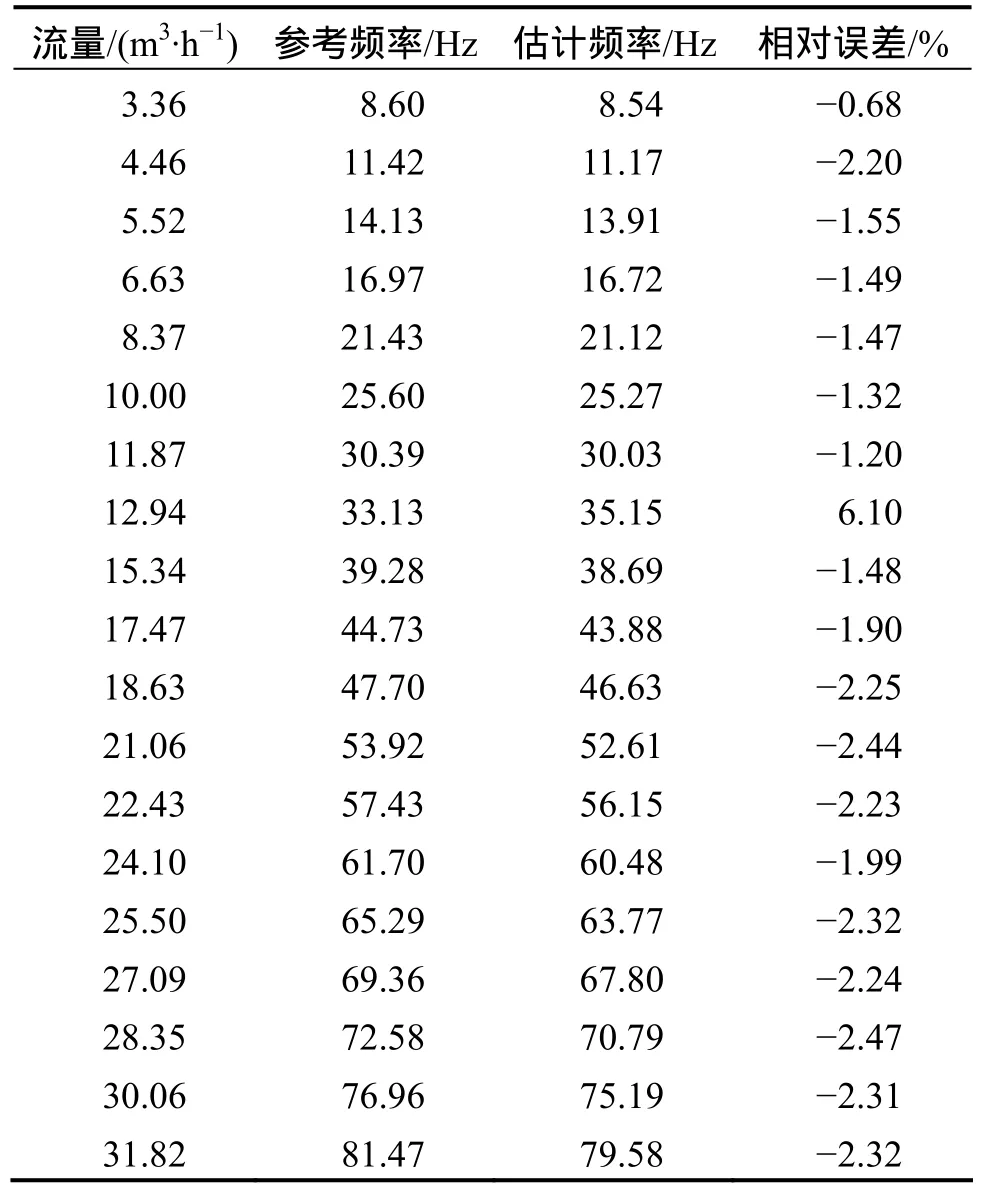
表1 旋涡脱落频率估计性能Table 1 Estimation results of vortex shedding frequency

由于AR模型的阶次直接关系到Burg算法的谱估计精度和计算效率，因此，讨论阶次对涡街流量计旋涡脱落频率提取性能的影响具有重要价值。为此，从1至100逐渐增加AR模型的阶次，得到Burg算法在不同阶次时的旋涡脱落频率估计值，如图3所示，其中虚线代表旋涡脱落参考频率。

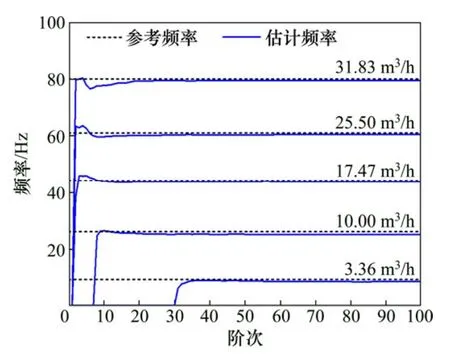
图3 AR模型阶次与旋涡脱落频率的关系Fig.3 Relationship between AR model’s order and vortex shedding frequency

图3表明AR模型阶次对基于Burg算法的旋涡脱落频率估计性能具有显著影响。当阶次较小时，频率估计值误差较大，特别是在旋涡脱落频率较低时尤为突出。在流量为3.36 m3/h、旋涡脱落频率为8.60 Hz时，AR模型阶次须大于32，估计频率的相对误差才能控制在±5%以内。进一步的试算结果表明，当旋涡脱落频率小于6 Hz时，基于Burg算法的AR模型谱估计对旋涡脱落频率的提取将失效，此时谱估计曲线出现剧烈波动。随着阶次的提高，Burg算法的频率估计性能逐渐稳定，与参考频率趋于一致，旋涡脱落频率的谱估计误差最终恒定在一个较低水平。随着频率的增大，谱估计所需的最低AR模型阶次不断降低。

利用 Burg算法实现高效高精度提取旋涡脱落频率的关键在于选择合适的AR模型阶次。对于不同频率的涡街流量计输出信号，应选用匹配的AR模型阶次。由图 3可知：Burg算法达到较高精度时的最低AR模型阶次随旋涡脱落频率的降低而呈现递增趋势。

在图3计算结果的基础上，定义AR模型最小阶次，即在该阶次下，基于Burg算法的旋涡脱落估计频率与参考频率的相对误差在±3%以内。图 4所示为AR模型最小阶次与旋涡脱落频率之间的关系。可见：随着旋涡脱落频率增加，AR模型最小阶次降低。

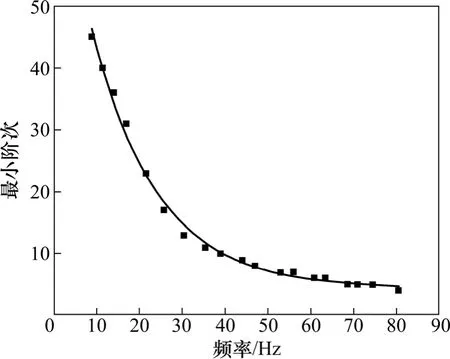
图4 AR模型最小阶次与旋涡脱落频率的关系Fig.4 Relationship between minimum AR model’s order and vortex shedding frequency

以正向取整ceil函数来描述AR模型最小阶次P与旋涡脱落频率f的关系，即

经对图4中的数据进行拟合后，得到

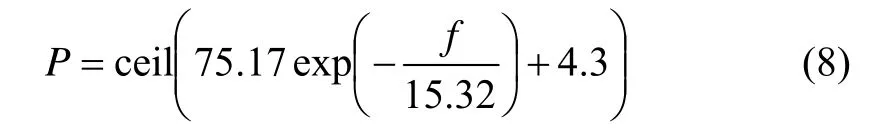
以上拟合的残差平方和为0.93，拟合系数为0.99，表明该曲线具有较高的拟合度。在采用基于Burg算法的AR模型谱估计时，根据式(8)可以先设定一个AR模型阶次的参考值，以保证旋涡脱落频率提取的精度。不建议采用低于参考值的阶次，否则可能导致谱估计误差过大。

选取相同实验条件下不同流量的涡街流量计输出信号验证式(8)的有效性。先按照式(8)计算出阶次的参考值，然后利用Burg算法计算该阶次下AR模型参数，估计旋涡脱落频率，结果列于表2。其中，参考频率为通过涡街流量计仪表系数计算得到的频率，相对误差的计算均以参考频率作为基准。

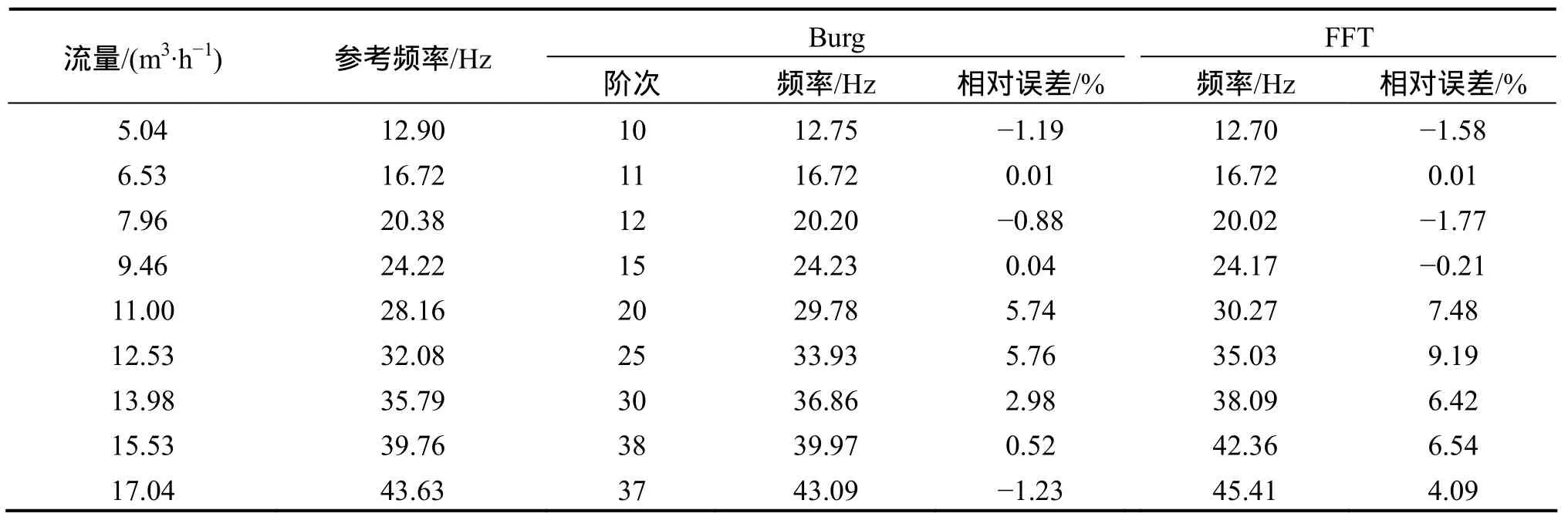
表2 最小AR模型阶次Burg估计与FFT结果Table 2 Results of Burg estimation under minimum AR model’s order and FFT

表 2同时还给出了采用快速傅里叶变换(fast Fourier transform，FFT)计算得到旋涡脱落频率及其相对误差。可见，在参考阶次下Burg算法频率估计的相对误差小于 6%，每个流量下的频率估计性能均优于FFT的计算结果，表明该方法对于涡街流量计旋涡脱落频率的提取精度较高，在工业上具有较好的实用性。

4 结论

(1) 基于Burg算法的AR模型谱估计适合于涡街流量计旋涡脱落频率的提取，频率估计值具有较高的精度，满足工程应用的要求。

(2) AR模型的阶次对Burg算法的谱估计精度和计算效率具有重要的影响，对于不同频率的涡街流量计输出信号，应选用匹配的AR模型阶次。

(3) 建立了频率相对误差小于3%的AR模型最小阶次与旋涡脱落频率的拟合关系式，AR模型最小阶次随旋涡脱落频率的增大而减小。

[1] Pankanin G L. The vortex flowmeter: various methods of investigating phenomena[J]. Measurement Science and Technology, 2005, 16(3): R1-R16.

[2] SUN Zhiqiang. Design and performance of the converging-diverging vortex flowmeter[J]. Metrology and Measurement Systems, 2011, 18(1): 129-136.

[3] SUN Zhiqiang. Mass flow measurement of gas-liquid bubble flow with the combined use of a Venturi tube and a vortex flowmeter[J]. Measurement Science and Technology, 2010,21(5): 055403.

[4] SUN Zhiqiang, ZHANG Hongjian. Measurement of the flow rate and volume void fraction of gas-liquid bubble flow using a vortex flow meter[J]. Chemical Engineering Communications,2010, 197(2): 145-157.

[5] Miau J J, Hu C C, and Chou J H. Response of a vortex flowmeter to impulsive vibrations[J]. Flow Measurement and Instrumentation, 2000, 11(1): 41-49.

[6] 黄咏梅, 张宏建, 孙志强. 涡街流量计的研究[J]. 传感技术学报, 2006, 19(3): 776-782.HUANG Yongmei, ZHANG Hongjian, SUN Zhiqiang. The development of vortex flowmeter[J]. Chinese Journal of Sensors and Actuators, 2006, 19(3): 776-782.

[7] Zhang T, Sun H, Wu P. Wavelet denoising applied to vortex flowmeters[J]. Flow Measurement and Instrumentation, 2004,15(5/6): 325-329.

[8] Amadi E, Zhu H, Higham E H. Analysis of signals from vortex flowmeter[J]. Flow Measurement and Instrumentation, 1993,4(4): 225-231.

[9] Hondoh M, Wada M, Andoh T, et al. A vortex flowmeter with spectral analysis signal processing[C]//Proceedings of Sicon'01 Sensors for Industry Conference. Rosemont: IEEE Press, 2001:35-40.

[10] Xu K, Huang Y, LÜ X. Power-spectrum-analysis-based signal processing system of vortex flowmeters[J]. IEEE Transactions on Instrumentation and Measurement, 2006, 55(3): 1006-1011.

[11] 孙志强, 周宏亮, 植晓琴, 等. 管内气液两相流涡街稳定性分析[J]. 中南大学学报: 自然科学版, 2008, 39(6): 1164-1169.SUN Zhiqiang, ZHOU Hongliang, ZHI Xiaoqin, et al. Analysis of the stability of gas–liquid two-phase vortex street in conduits[J]. Journal of Central South University: Science and Technology, 2008, 39(6): 1164-1169.

[12] 桑文慧, 孙志强, 周孑民. 有限流道内低雷诺数二维圆柱绕流数值模拟[J]. 中南大学学报: 自然科学版, 2012, 43(3):1166-1170.SANG Wenhui, SUN Zhiqiang, ZHOU Jiemin. Numerical simulation of two-dimensional flow around a circular cylinder at low Reynolds numbers in finite channel[J]. Journal of Central South University: Science and Technology, 2012, 43(3):1166-1170.

[13] SUN Zhiqiang, ZHOU Jiemin, ZHOU Ping. Application of Hilbert-Huang transform to denoising in vortex flowmeter[J].Journal of Central South University of Technology, 2006, 13(5):501-505.

[14] 孙志强, 张宏建. 涡街流量计信号的高阶统计量特征[J]. 传感技术学报, 2007, 20(7): 1542-1545.SUN Zhiqiang, ZHANG Hongjian. Higher-order statistics characteristics of vortex flowmeter signals[J]. Chinese Journal of Sensors and Actuators, 2007, 20(7): 1542-1545.

[15] 孙志强, 张宏建. 涡街流量计信号能量的功率谱式表征与应用[J]. 传感技术学报, 2007, 20(8): 1800-1804.SUN Zhiqiang, ZHANG Hongjian. Power spectrum based representation of vortex flowmeter signal energy and its application[J]. Chinese Journal of Sensors and Actuators, 2007,20(8): 1800-1804.

[16] 韩春林, 何子述. 基于 Burg叠代的多径信号DOA估计算法[J]. 通信学报, 2003, 24(7): 24-29.HAN Chunlin, HE zishu. A DOA estimation algorithm for multipath signals based on Burg iterations[J]. Journal of China Institute of Communications, 2003, 24(7): 24-29.

[17] 姚文俊. 自相关法和Burg法在AR模型功率谱估计中的仿真研究[J]. 计算机与数字工程, 2007, 35(10): 32-34.YAO Wenjun. Research on AR model power spectrum estimation based on the algorithm and Burg algorithm[J].Computer and Digital Engineering, 2007, 35(10): 32-34.

[18] ZHANG Hongjian, HUANG Yongmei, SUN Zhiqiang. A study of mass flow rate measurement based on the vortex shedding principle[J]. Flow Measurement and Instrumentation, 2006,17(1): 29-38.