不同温度的水岩作用对岩石节理表面形貌特征的影响
曹平,宁果果,范祥,梅慧浩,黄雪姣
(中南大学 资源与安全工程学院,湖南 长沙,410083)
地下工程中岩体基本都存在的大量节理、裂隙等不同连续面,破坏了岩体的连续性和完整性,由于其几何形态和力学形态上的复杂性,对地下工程产生深远的工程影响。关于岩体节理表面形貌的研究已经有大量成果,如Barton等[1]提出用节理粗糙度系数(JRC)评价节理表面粗糙程度的方法,从一定意义上可以满足工程需求;夏才初等[2]在统计学的基础上描述岩体表面二维形貌特征,值得借鉴。随着精确测量表面形貌仪器的改进,由机械触针式岩石表面形貌仪发展为智能型岩石表面形貌仪(RSP−Ⅰ)和便携式表面形貌仪(TJXW−3D),为节理表面形貌参数精确扫描分析提供技术支持[2−3]。地下岩层环境中的水与岩石之间的水岩耦合作用也对岩体节理面的物理性能、工程强度等特性产生很大程度的影响,曹平等[4−6]利用三维激光形貌仪研究节理面在循环压剪作用下表面形貌的变化规律。随着地下矿山开采深度增加,面临着地热高温的灾害工程问题,矿井工作面温度达 50 ℃,部分高达60 ℃[7],已有研究表明:高温条件下的岩石的基本物理性能和力学响应机制和常温相比差异较大[8−9]。地下工程岩石由于其特殊的赋存环境,地应力场以及地下水渗流场、温度场及其耦合作用对岩体基本物理参数和力学性质具有重要影响[10−11]。目前国内外关于水岩作用的研究大多是从渗流场—应力场—温度场等多场耦合角度出发,分析研究力学响应机制[12−13]。地下岩体及其环境的耦合作用本质都是细观上乃至微观颗粒的物理反应或化学反应导致的岩体从表面到内部的离子、粒子、矿物颗粒等的交换、迁移和流失等,岩石表面细观形貌特征的改变是岩体力学响应机制的基础。Clarke等[14−17]将分形理论引入岩石力学形貌学,利用分形维数描述表面形貌特征的粗糙度等参数,目前被广泛采用;在此基础上,Chen等[18]利用三维表面激光形貌仪研究水岩作用对节理表面形貌的影响,建立了特定形貌参数和岩体物理特性的定量关系。通过扫描测量得到的形貌表面的参数,结合岩石节理面力学特性,可以得出岩石表面形貌和岩石力学性能的力学响应机制;另外水腐蚀损伤对岩石力学性质有弱化作用,能加快岩体微裂纹的扩展[19]。基于此,本文作者进行不同温度条件下水岩耦合作用对岩石节理表面形貌参数的规律研究,揭示温度场水岩作用的影响机理,为地下岩体工程施工过程提供理论依据。
1 试验设计及过程
考虑到软岩遇水膨胀特性对实验的观察结果存在较大的干扰,影响温度对水岩作用效应的准确判别,因此本实验选取的2种岩样为典型的硬岩岩样。由于岩石节理表面在空气中存在风化和水化等作用,为得到原始的新鲜完好的节理表面,本试验利用巴西劈裂法制作人工岩石节理样本,如图1和2所示。2种岩样的基本力学参数参见表1。

图1 巴西劈裂法示意图Fig.1 Sketch of Brazil splitting method
考虑到实际地下工程的高温条件,试验设计的温度分别为20 ℃,40 ℃,60 ℃和80 ℃共4个不同观测温度。试验中的水岩作用的保持温度恒定,由室内恒温箱控制,不同的温度下水岩作用时间均设定为48 h,恒温箱中岩石浸泡在自然水中(pH=7)。从水岩作用的时间效应来看,48 h的水岩作用时间相对于实际工程中岩石与水的长期作用不能比拟,由于只考虑到节理表面的形貌变化,48 h的浸泡时间是可行的。
本实验采用先进的Talysurf CLI2000三维表面激光形貌仪,该仪器为全自动激光扫描,扫描过程由内置计算机操作系统控制,而扫描结果分析由配套的分析软件Talymap Gold执行,智能化程度高,扫描精确度可达0.5 μm,且扫描过程对节理试样没有损伤。
本实验的恒温系统采用的501系列的超级恒温水槽,恒温槽由智能化的微机控制,选用整体耐高温的玻璃槽体,通体透明,便于观察试验变化。其温度控制范围为室温+5 ℃~95 ℃,温度波动度为±0.05 ℃。槽内设有循环水泵,泵流量为8 L/min,保证水槽内的温度均匀。
本实验研究温度−岩石节理表面形貌变化响应机制,设计不同温度的水岩作用对节理表面形貌影响试验,设计路线分别如图3所示。
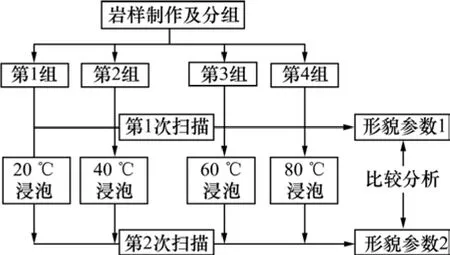
图3 不同温度水岩作用试验路线图Fig.3 Diagram of experiment procedure
不同温度下连续水岩作用对节理表面形貌影响试验具体步骤如下:
第 1步,利用巴西劈裂法制作得到长×宽为 50 mm×50 mm岩石人工节理面,并分别分组编号;
第2步,将试样在常温下烘干并保持干燥,选取形貌仪的分辨率为10 μm对每个试样对表面形貌进行第1次扫描,并保存扫描结果;
第3步,将试样独立浸泡在盛有自然水的容器中,并置于恒温箱中,调节恒温箱温度为20 ℃。为了取得与实际工程中的相近的地下水条件,容器无须密封,充分保证试样与自然介质的充分接触;
第4步,试样在浸泡持续48 h后取出,并置于扫描仪再次扫描,扫描仪参数设置与第一次扫描相同,得到第2次扫描结果;
第5步,重复上述第3和第4循环步骤2次,不同之处在于恒温箱温度分别设置为40 ℃,60 ℃和80℃,得到不同温度条件的节理表面形貌扫描结果;
最后,将得到的不同温度下水岩作用前后的扫描结果,借助分析软件Talymap Gold对其进行节理表面形貌参数的变化研究分析,探索研究温度变化与岩石节理表面形貌参数之间的变化规律。
2 试验结果数据分析
本次试验采用的数据分析软件为仪器附带的Talymap Gold,主要是采集节理表面形貌的三维形态参数,包括分形参数和高度特征参数2种类型。为了减少数据的离散性,下文提及的所有数据均为有效数值,具体的数据处理方法如下式:

2.1 表面形貌分形参数与温度变化规律研究
岩体节理表面形貌是极其不规则的,用分形维数能揭示其本质的空间特征[12−14]。分形理论仅用分形维数来描述岩体不连续表面的几何粗糙特性,即分形维数越大,粗糙线的起伏越厉害,分形维数表明了小尺寸范围内不连续面的高级次起伏程度。
本试验利用扫描岩样得到的表面形貌参数,精确地获取节理的真实形貌,然后研究该形貌的分形维数,并寻找不同温度下的水岩作用对节理表面形貌影响和分形维数之间的变化规律。计算节理表面形貌分形参数有多种方法,软件Talymap Gold使用的是盒维数法。具体计算方法为[16]:
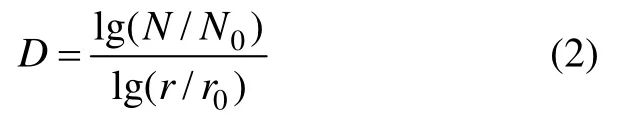
式中:r0为初始的测量间距;r为计算立方体的边长;N为覆盖粗糙表面所用的边长为r立方体的个数;N0为覆盖粗糙表面所用的边长r0立方体的个数。
通过软件分析得到的分形参数如图 4所示(以片麻岩2号试样为例)。本研究使用图表中包含的3个分形参数为分形维数(D)、回归线斜率(k)和回归线相关系数(R2),其中:分形维数D于回归线斜率呈现互为相反数关系,即D=−k。
试验全部的岩样的分形维数D和回归线相关系数R2分别如表2和表3所示。
通过表2和3数据分析可知:经过不同温度的水岩作用后,岩样表面形貌分形参数均有一定程度的变化,在20 ℃,40 ℃和60 ℃条件下,分形维数D都随着水岩作用而增加,且不同温度下的改变程度有所区别,而在80 ℃则情况相反,D在水岩作用后有一定程度减少。而对于相关系数R而言,它反映的是计算分形维数精确度,从表2和3可知:经过不同温度水岩作用后的节理表面形貌分形参数精确性均有所提高。
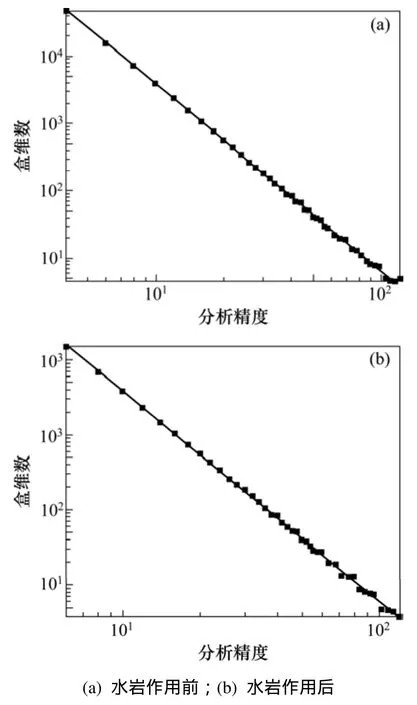
图4 水岩作用前后分形维数图(片麻岩2号试样)Fig.4 Fractal dimension figure before and after water-rock interaction(Gneiss No.2)
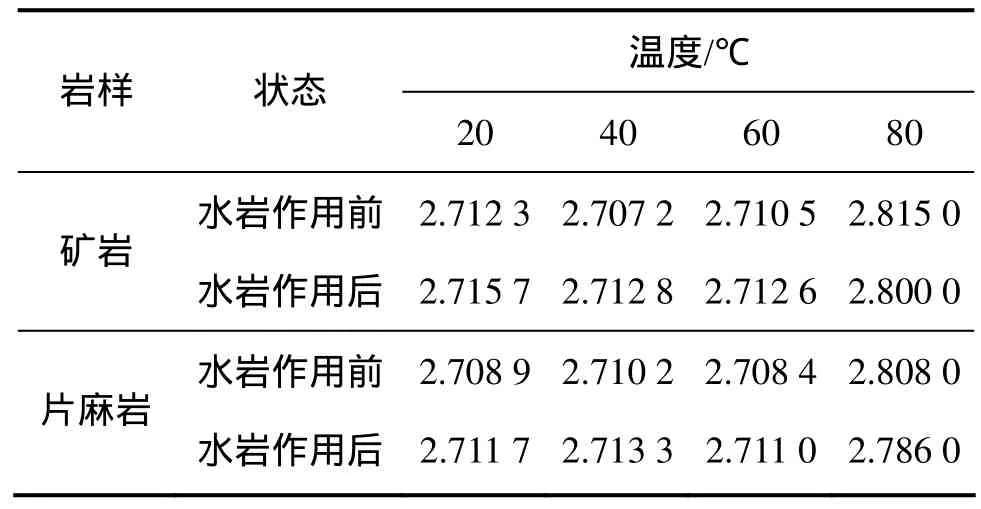
表2 岩样分形维数D统计表Table 2 Fractal dimension of rock samples
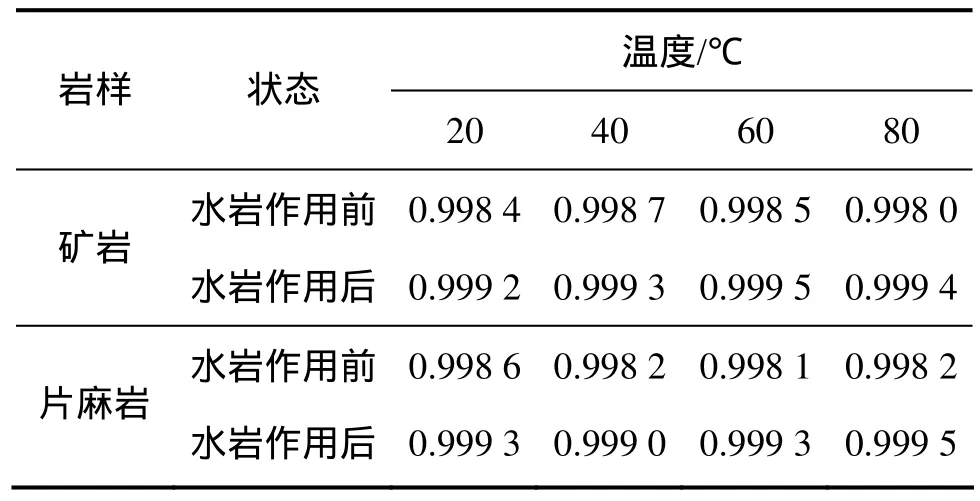
表3 回归线相关系数R2统计表Table 3 Regression correlation coefficient
本文作者认为其原因是温度增加一定程度上促进了水岩作用,表面形貌变得更加复杂和凹凸不平,各向异性更加明显。根据表3可知:在一定范围内(本试验研究的温度范围为20~60 ℃),温度在水岩作用中扮演着“催化”的功效,从分形参数来看,温度越高,相对分形参数ΔD和ΔR变化越大,这意味着温度越高,水岩作用越剧烈,节理表面形貌参数改变增大,对应的分形参数变化得越明显,形貌的粗糙度和各向异性增加;当温度超过某一特定的温度临界值时,从形貌分形维数来看,温度对水岩作用起到的功效恰恰相反,温度升高降低了表面形貌的粗糙度和各向异性。
由于岩样的初始分形参数不同,不同温度的分形参数变化量没有统一的参照标准。为研究分形参数变化和温度之间的关系,根据数理统计学原理引入一个相对分形参数变化ΔD,其中:
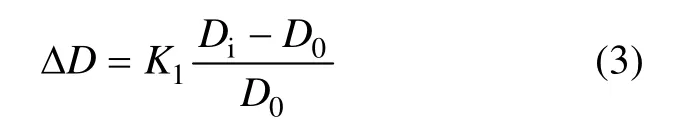
式中:K1为放大系数,便于分析变化情况,本研究取K1=1 000;D0和Di分别为水岩作用前、后的分形维数。
根据式(3)和表2中的数据,计算可得相对分形参数变化量,如表4所示。
通过拟合表4中的数据,可以得到相对分形维数的变化量ΔD与温度t的关系曲线,如图5所示,其函数关系表达式为:
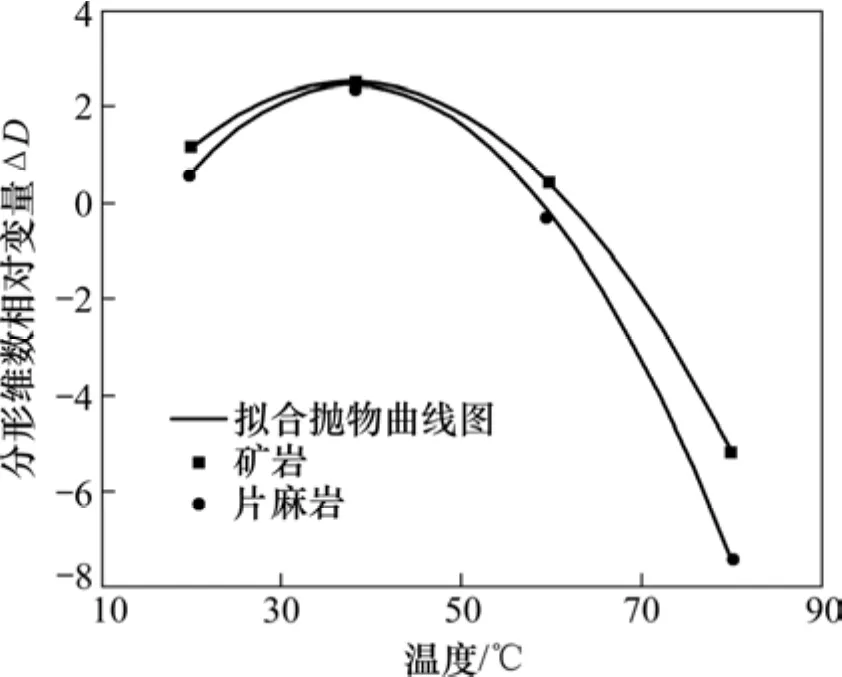
图5 温度−相对分形维数变量拟合曲线图Fig.5 Fitting curve of temperature and relative fractal dimension variation
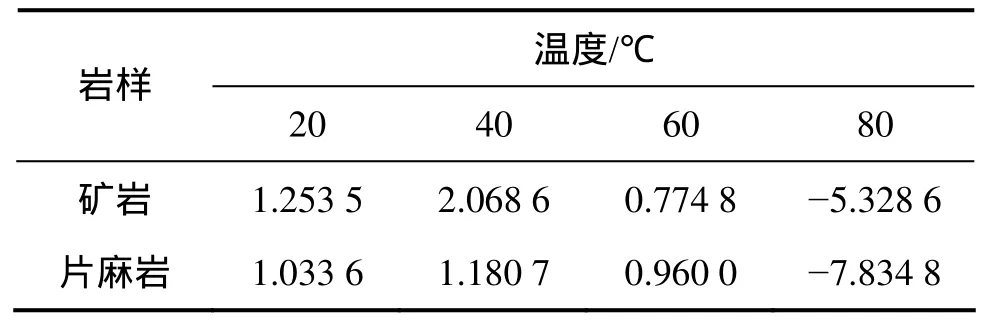
表4 相对分形维数ΔD变化Table 4 Relative fractal dimension variation ΔD

式(4)揭示温度对形貌分形维数的影响规律。根据图5可知:对于试验中2种岩性而言,相对分形维数变化量均在40℃左右最大,为温度临界值,在20~40℃呈正增长趋势,在40~80 ℃则呈负增长规律,负增长的速率相比于正增长速率更大。
2.2 数理统计参数变化
本研究引用数理统计参数包括高度分布标准均方偏差 Sq、偏态系数(偏度)Ss、高度分布峰态系数 Sk、峰点密度Spd,它们的计算表达式[18]分别为:

形貌参数的统计参数可以反映出形貌的变化情况,Sq能够较好地反映形貌的整体性粗糙程度、离散性和波动性,Ss为高度分布偏态系数,有正负偏态 2种情形,正偏态系数说明表面形貌存在大量的峰点和突出,而负偏态则说明表面形貌组成主要是在一个平稳的“高原”和较好的“深谷”。Sk表明形貌的高度分布形状,反映其峰度和峭度,Spd表征单位表面面积内峰点的平均数量,其中峰点的判定规则为:在某特定区域范围内中的一点均高于任何其他8个点,则该点被视为峰点。
扫描分析所得的统计参数如表5所示。通过表5计算可知:2种不同岩性的岩样形貌统计参数在不同温度下的水岩作用后均发生变化,且变化程度在不同温度条件存在差异。
对于高度分布标准均方偏差Sq而言,2种岩性在20 ℃时的水岩作用前后分别增加了 102.07%和51.76%,40 ℃时分别为134.26%和62.41%,60 ℃时分别为157.59%和77.55%,80 ℃时分别为51.58%和37.33%。
对于偏态系数(偏度)Ss,2种岩性在水岩作用后都有负偏态变为正偏态,由此可知:水岩作用改变了表面形貌峰点高度分布情况。在20 ℃条件下水岩作用前后改变了 205.34%和 130.12%,在 40 ℃时分别为214.86%和 192.92%,60℃时分别为 471.33%和181.94%,80 ℃时分别为105.59%和144.24%。
对于高度分布峰态系数Sk,2种岩性在不同温度水岩作用下均发生不同程度的变化,20 ℃时的变化分别为29.48%和30.41%,在40 ℃时分别为36.85%和27.14%,60 ℃时分别为166.27%和33.27%,80 ℃时分别为22.96%和22.83%。
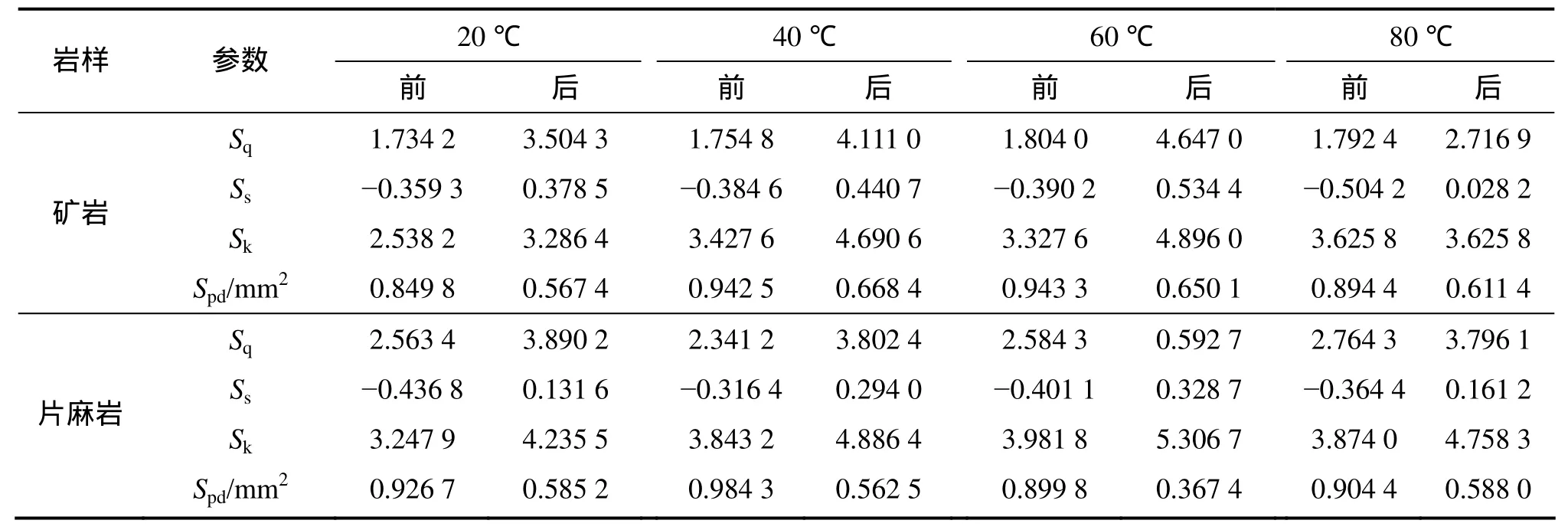
表5 岩样数理统计参数Table 5 Mathematical statistics parameters of samples
对于峰点密度Spd,在水岩作用前后均减少,且不同温度下变化不一,在20 ℃时其分别减少了33.44%和36.85%,40 ℃时分别为29.08%和42.85%,60 ℃时分别为 31.08%和 59.17%,80 ℃时分别为 31.64%和34.98%。
由此可以得出:不同的温度条件下,岩石节理表面形貌参数变化存在较大差异。为深入分析温度改变对水岩作用的影响机制,引入相对温度应变参数,即温度敏感性系数ts,其中

式中:Δε为不同温度水岩作用前后参数改变率;Δt为温度改变量。
根据式(6)可得2种岩性各数理统计参数的温度敏感性参数如表6所示。
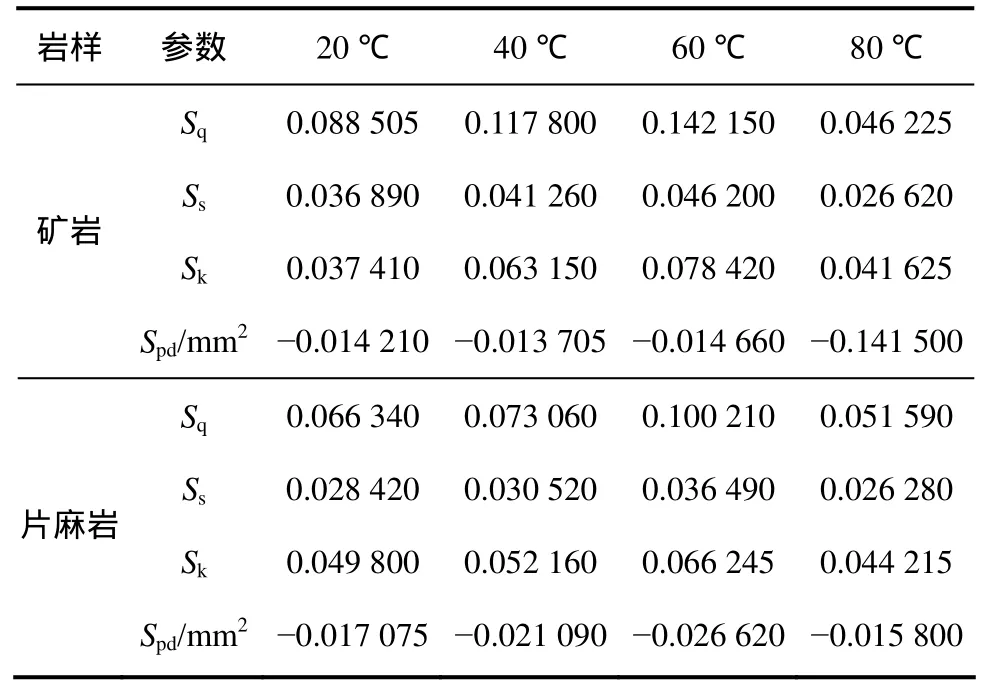
表6 数理统计参数温度敏感性系数Table 6 Temperature sensitive coefficient of mathematical statistics parameters ℃−1
通过表6可知:在一定温度范围内(20~60 ℃),形貌数理统计参数对温度的敏感度增加,随着温度的升高,水岩作用对岩石表面形貌的参数变化影响程度呈扩大趋势,这意味温度可以加速水岩作用反应,当温度超过一定程度(60~80 ℃)时,形貌参数的变化对于温度改变的敏感性逐渐降低。参数温度敏感性极值点tms在60~80 ℃之间。其中对温度敏感性最强的为Sq,而敏感性最差的为Spd,对于水岩作用而言,温度的改变最直接的影响是岩石表面形貌中的高度特征,进而再影响到与高度特征参数有关的Sk和Spd等参数值。
3 结论
(1) 在20~60 ℃温度条件下水岩作用后,岩石表面形貌分形维数的相对变化量ΔD随着温度升高而升高,在60~80 ℃范围则随着温度升高而降低。
(2) 拟合曲线得到相对分形维数ΔD和温度t二者之间的关系为:ΔD=−1.729 6t2+6.544 1t−3.696,R²=0.989 4(矿岩);ΔD=−2.235 5t2+8.494 8t−5.636,R²=0.943 3(片麻岩),曲线得出的温度临界值为40 ℃。
(3) 温度变化对形貌数理统计不同参数变化的影响有一定差异性,但均存在一个温度敏感极值点(本研究为 60~80 ℃之间),且当温度低于温度敏感极值点时,温度的升高可以促进水岩作用,而高于温度敏感极值点时,水岩作用对温度的敏感性明显降低。
(4) 本实验所用的温度值间隔为 20 ℃,区间为20~80 ℃,精度和范围均有一定的局限性,本研究结论对于低温或更高温的条件不一定适用,有待进一步研究。
[1]Barton N, Bandis S.Review of predictive capabilities of JRC-JCS in engineer practice[C]//Proc Int Rock Joints.Norway,1990: 603−610.
[2]夏才初, 孙宗颀.工程岩体节理力学[M].上海: 同济大学出版社, 2002: 18−29.XIA Caichu, SUN Zongqi.Engineering mechanics of rock joints[M].Shanghai: Tongji University Press, 2002: 18−29.
[3]邾继贵, 王浩, 任同群, 等.便携式激光扫描三维形貌测量系统[J].机械工程学报, 2005, 41(2): 166−169.SHU Jigui, WANG Hao, REN Tongqun, et al.Portable laser scanning system for 3D contour measure[J].Chinese Journal of Mechanical Engineering, 2005, 41(2): 166−169.
[4]曹平, 范祥, 蒲成志, 等.节理剪切试验及其表面形貌特征变化分析[J].岩石力学与工程学报, 2011, 30(3): 480−486.CAO Ping, FAN Xiang, PU Chengzhi, et al.Shear test of joint and analysis of morphology of joint surface[J].Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 480−486.
[5]Grassellia G, Wirth J, Egger P.Quantitative three-dimensional description of a rough surface and parameter evolution with shearing[J].International Journal of Rock Mechanics and Mining Sciences, 2002, 39(6): 789−800.
[6]Belem T, Souley M, Homand F.Method for quantification of wear of sheared joint walls based on surface morphology[J].Rock Mechanism and Rock Engineering, 2009, 42: 883−910.
[7]张俊杰.深部开采优化开采技术的探讨[J].矿山地压与顶板管理, 2005, 22(3): 74−78.ZHANG Junjie.Study on deep mining optimization of the mining technology[J].Mine Pressure and Ceiling Management,2005, 22(3): 74−78.
[8]方荣, 朱珍德, 张勇, 等.高温和循环高温作用后大理岩力学性能试验研究与比较[J].岩石力学与工程学报, 2005, 24(增1):4735−4742.FANG Rong, ZHU Zhende, ZHANG Yong, et al.The study and comparison of the mechanical performance of Marble under the action of high temperature and circle high temperature[J].Chinese Journal of Rock Mechanics and Engineering, 2005,24(S1): 4735−4742.
[9]张连英, 茅献彪, 卢爱红, 等.高温作用下岩石力学性能的实验研究[J].中国科学: 技术科学, 2010, 40(2): 157−162.ZHANG Lianying, MAO Xianbiao, LU Aihong, et al.Experimental study on the mechanical properties of rock at high temperature[J].Sci China Ser E: Tech Sci, 2010, 40(2):157−162.
[10]Chijimatsu M, Fujita T, Kobayashi A, et al.Experiment and validation of numerical simulation of coupled thermal, hydraulic and mechanical behaviour in the engineered buffer materials[J].International Journal of Numerical and Analytical Methods in Geomechanics, 2000, 24: 403−424.
[11]周创兵, 陈益峰, 姜清辉.岩体多场广义耦合及其工程应用[J].岩石力学与工程学报, 2008, 27(7): 1330−1340.ZHOU Chuangbing, CHEN Yifeng, JIANG Qinghui.On generalized multi-field coupling for fractured rock massed and its application to rock engineering[J].Chinese Journal of Rock Mechanics and Engineering, 2008, 27(7): 1330−1340.
[12]Rutqvist J, Borgessonb L, Chijimatsuc M, et al.Thermo-hydromechanics of partially saturated geological media governing equations and formulation of four finite element models[J].International Journal of Rock Mechanics and Mining Sciences, 2001, 38: 105−127.
[13]Rusqvist J, Barr D, Datta R.Coupled thermalhydrological-mechanical analyses of the Yucca mountain drift scale test: Comparison of filed measurement to predictions of four different numerical models[J].International Journal of Rock Mechanics and Mining Sciences, 2005, 42: 680−697.
[14]Clarke K C.Computation of the fractal dimension of topographic surfaces using the triangular prism surface area method[J].Computer and Geosciences, 1986, 12(5): 713−722.
[15]周宏伟, 谢和平, Kwasniewski M A.粗糙表面分维计算的立方体覆盖法[J].摩擦学学报, 2000, 20(6): 455−459.ZHOU Hongwei, XIE Heping, Kwasniewski M A.Fractal dimension of rough surface estimated by the cubic covering method[J].Tribology, 2000, 20(6): 455−459.
[16]谢和平.分形几何及在岩石力学中的应用[J].岩土工程学报,1992, 14(1): 14−24.XIE Heping.Fractal geometry and its application in the rock mechanics[J].Chinese Journal of Geotechnical Engineering,1992, 14(1): 14−24.
[17]吴爱祥, 姚高辉, 王贻明, 等.浸出过程中矿石颗粒表面微孔裂隙演化规律[J].中南大学学报: 自然科学版, 2012, 43(4):1462−1468.WU Aixiang, YAO Gaohui, WANG Yiming, et al.Evolution rules of micropores and microfracture on surface of ore particles in heap leaching[J].Journal of Central South University: Science and Technology, 2012, 43(4): 1462−1468.
[18]CHEN Yu, CAO Ping, CHEN Rui.Effect of water–rock interaction on the morphology of a rock surface[J].International Journal of Rock Mechanics and Mining Sciences, 2010, 47:816−822.
[19]汪亦显, 曹平, 陈瑜, 等.膨胀性软岩水腐蚀损伤断裂力学效应实验研究[J].中南大学学报: 自然科学版, 2011, 42(6):1685−1691.WANG Yixian, CAO Ping, CHEN Yu, et al.Testing study on damage and fracture mechanical effects for swelling soft rock during water corrosion[J].Journal of Central South University:Science and Technology, 2011, 42(6): 1685−1691.

