基于带面内转角自由度四节点平板壳单元的板壳非线性分析

文颖，戴公连，曾庆元

(中南大学 土木工程学院，湖南 长沙，410075)

薄板、薄壳结构具有较高的面内强度、结构自重轻、便于工场预制以及现场拼装等优点，在大型土木工程结构，例如大跨度桥梁主梁(板梁、箱梁、组合梁)，大跨度屋盖结构以及近海钻井平台等获得广泛应用，受到结构工程师们普遍关注。其设计计算理论已从基于微分方程的经典解析法发展到以有限单元法为代表的数值分析方法[1]。板壳有限元，与杆系有限元一样，都是有限元理论体系的重要组成部分[2]。平板壳单元作为一类应用较多的板壳单元，历来是研究的热点。根据单元变形特点，这些研究成果可集中分成2种类型：一类是反映单元面内变形的膜位移分析，另一类则是单元面外挠曲变形分析。国内外学者在板壳单元膜位移分析领域做了大量工作，龙驭球等[3]总结了这些理论研究成果。学术界普遍认为单纯按节点线位移插值得到单元膜位移场一般会引入虚假应变而影响计算结果精度。虽然采用缩减积分，加密有限元网格等手段可以一定程度上弥补上述不足，但也带来多余零能模式，增加建模工作量等问题。目前公认的解决方案是考虑节点面内转角自由度的贡献[2,4],这样既可以在保证单元具有同等位移精度条件下减少单元自由度数又可解决组装由共面单元离散的板壳结构刚度矩阵时由于各单元面内转角自由度的缺失而导致整体刚度矩阵病态问题。为此，Allman[5]提出了平面膜元的二阶位移场理论。朱菊芬等[6]基于Allman方法将单元膜位移表示成由节点线位移插值得到的基本位移场和考虑节点旋转自由度影响的高次位移场的叠加，以避免剪切闭锁与零能位移模式。Long等[7]基于广义协调元理论提出一系列高性能膜单元，例如 GT9，GT9M，GR12和GQ12等。冯仲齐等[8]通过引用连续介质力学中旋转度的概念构造边界位移按三次变化的 Q20单元，便于与一维梁单元的衔接。夏桂云等[9]将节点角位移作为旋转自由度用有限条带构造单元，具有列式简单、物理概念清晰等特点，可是节点刚性假定增加了单元刚度。此外，也有学者提出单元线位移与转角变位独立插值以减轻单元“过刚”现象[4,10]。平板壳单元的面外挠曲分析通常分为2种类型[10]，即不考虑单元横向剪切变形的 Kirchhoff型单元和计入剪切变形影响的Reissner-Mindlin(R-M)型单元。R-M板壳元虽然只要求C0类连续，但在实际应用时容易产生剪切闭锁。Kirchhoff型单元因为列式简单明了，计算效率高而在薄板、壳结构分析方面获得广泛应用。国内外学者在构造非协调与协调 Kirchhoff型薄板弯曲单元方面进行了大量研究。本文作者在总结前人工作的基础上，提出一种面内、面外变形协调的四节点平板壳单元。采用有限条带描述单元整体位移场。其中，膜位移场由包含节点转角自由度在内的节点位移参数沿纵、横向条带顺次插值得到，横向弯曲变位则表示为双三次Hermite多项式乘积形式。该单元模型确保位移及应变分量在单元内部和相邻单元之间连续，物理概念明确，分析精度高。通过选取矩形薄板弹塑性分析和圆柱壳体大变位、大转动2个经典算例，说明本文提出的板壳单元位移模型可以有效解决一般板壳结构稳定极限承载力分析问题。

1 四节点平板壳单元列式

1.1 基本假定

(1) 单元面外挠曲变形满足Kirchhoff假定，即单元截面法线在单元变形后仍为直线且保持与单元中面垂直，忽略横向剪切变形对单元挠度影响。其次，忽略单元纤维沿截面厚度方向挤压变形。

(2) 基于Von-Karman大挠度、小应变理论，大变位状态下单元应变只计入挠度w对面内坐标x，y直至二阶非线性偏导数的影响，忽略面内位移u，v对坐标x，y非线性偏导数的影响。

1.2 单元空间位移场

首先选取局部坐标系xyz作为描述单元变形的参考系，如图1所示。坐标系原点O位于单元任意一节点i，x轴和y轴均通过单元的中面且分别与单元边界ij和边界 il重合，z轴垂直于单元中面且与x轴和 y轴满足右手螺旋法则。单元每个节点(角点)有 7个自由度：3个空间线位移自由度u，v，w，3个空间转动自由度θx，θy，θz和一个扭转率自由度κ，这样单元共有28个自由度。本文中行向量用 表示，列向量用｛｝表示，矩阵用[]表示，下标“，”表示对紧跟着的变量求导数，而变量出现次数就是求导的 阶数。

根据基本假定 1且忽略单元沿厚度方向挤压变形，单元内部任意一点的位移可以表示为：

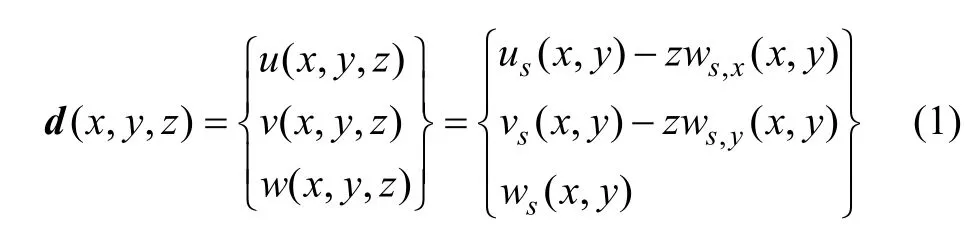
式中：us，vs和ws分别表示单元中面内任意点沿x，y，z坐标线位移；ws,y=θx，-ws,x=θy则分别表示单元截面绕x，y坐标轴旋转角位移。

为了确定单元中面线位移 us(x，y)，可假想将单元沿y方向离散为连续的横向条带。条带上各点位移

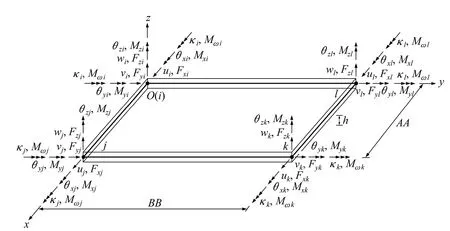
图1 四节点平板壳单元Fig. 1 A four-node flat shell element

认为沿x方向线性变化，同时假定条带端点位移沿y方向也满足线性变化规律，即有

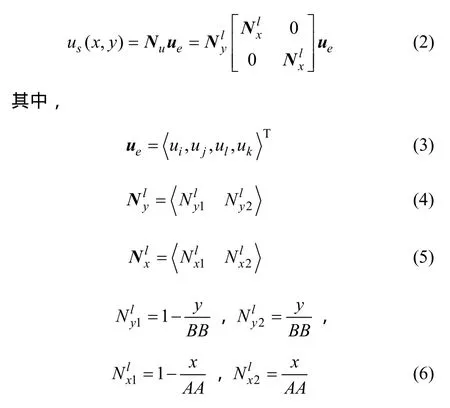
对于单元中面线位移 vs(x，y)，也可以假想沿 x方向单元被划分成连续分布的条带。条带上各点y方向位移沿着条带方向按3次Hermite多项式变化，而条带端点y方向位移又可沿x方向线性插值得到。因此，

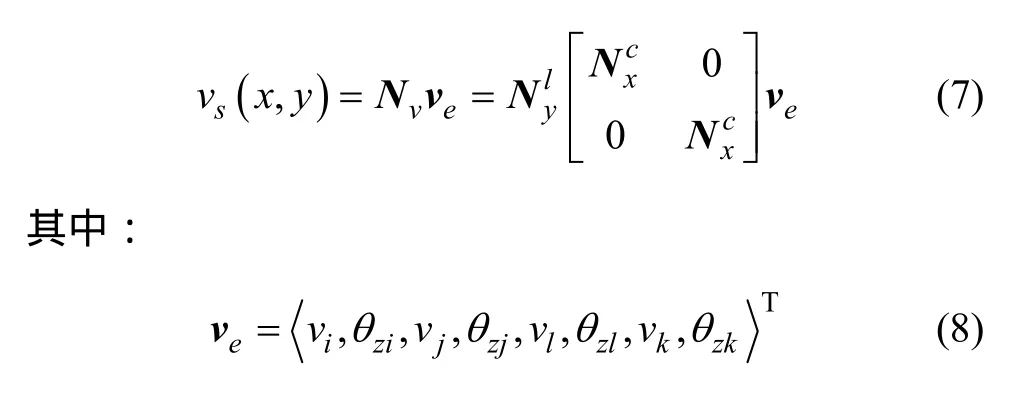
式中：θzi，θzj，θzk，θzl表示单元节点面内旋转自由度，这些转角自由度对单元面内位移的影响通过式(7)表示。这样既可保证单元边界位移相互协调，又可避免单元节点“过刚”而影响计算结果精度。

单元中面面外挠曲位移ws(x，y)可以通过沿x和y方向分别3次Hermitian插值得到[11]，即有

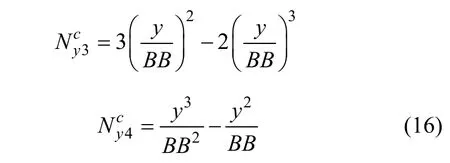
需要注意的是，上述单元空间位移模式具有 C1连续性，即在单元边界上线位移和转角是协调的；通过引入单元节点面内自旋自由度，克服了一般板壳单元处理单元面内旋转刚度不便的缺点，因此具有较好的分析精度和较强的适用性。

1.3 单元应变度量

由前述基本假定 1可知，单元应变分量εxz=εzx=εyz=εzy=εzz=0，非零应变分量包括 εxx，εyy，εxy和εyx。又因为剪应力互等εxy=εyx，剩下3个非零独立应变分量：正应变 εxx，εyy和剪应变 εxy。将这些应变张量分量写成工程应变形式[12]，当不考虑单元大位移影响时，有

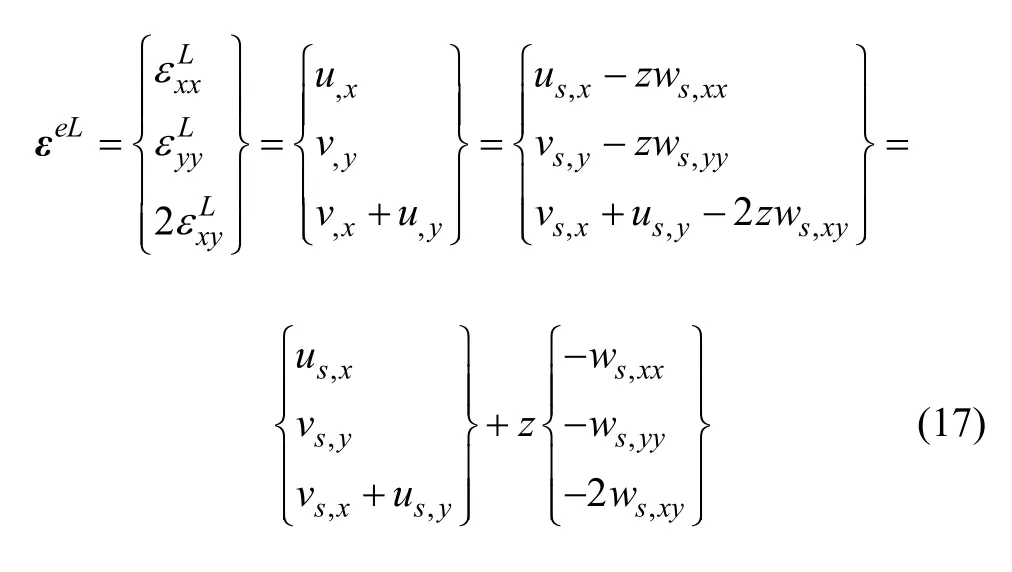
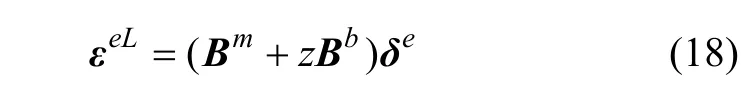
其中：

将式(2)，(7)和(12)代入式(17)，式(17)可缩写成：

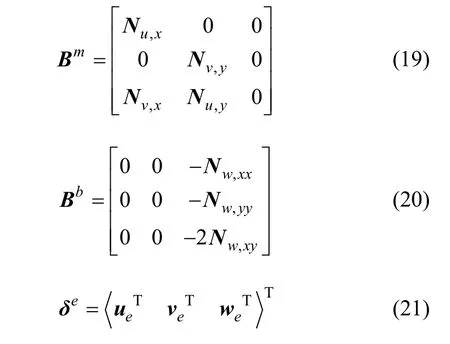
当分析单元大位移、大转动问题时，需要计及几何非线性应变的影响[13]，根据基本假定1和2，有

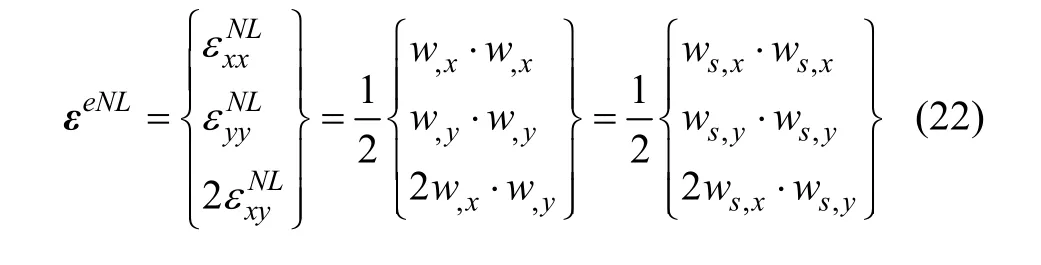
将式(12)代入式(22)后得：

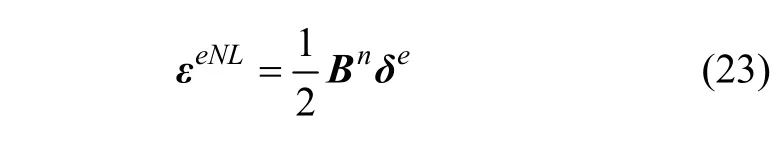
其中：

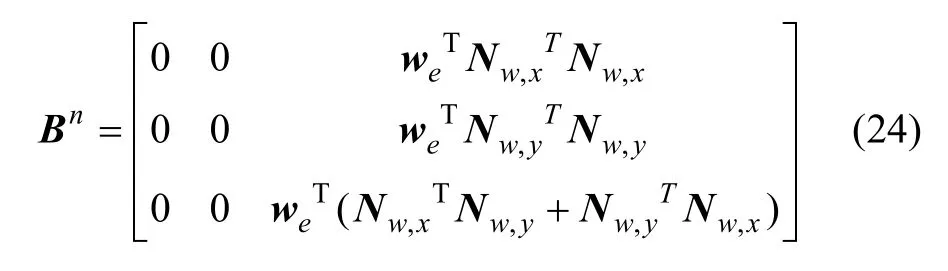
由式(18)和式(21)，可得一般情况下单元应变度量为：

1.4 单元刚度矩阵

根据连续介质力学理论，单元任意程度变形均可表示成一系列连续有限变形过程。对于一典型有限变形又可由经典Updated-Lagrange列式描述，由此可得线性化的增量平衡方程如下[14]：

其中：D为当前增量变形步内应力-应变本构关系；tσe为单元产生增量变形之前(t时刻)Cauchy应力分量列向量；t+dtR则为单元产生增量变形后(t+dt时刻)节点外荷载列向量。将式(18)和式(21)代入式(23)可得：

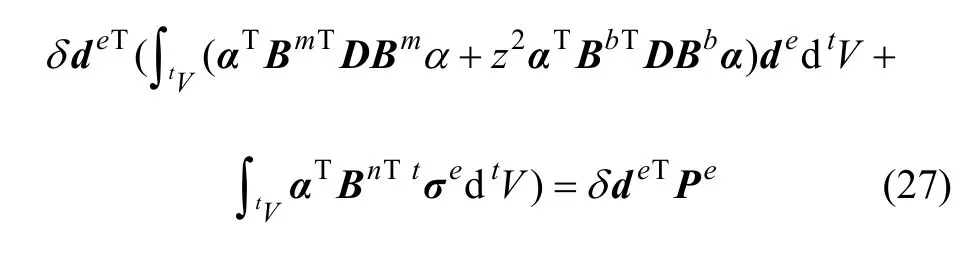
α为系数矩阵且有 δe=αde。进一步整理后式(27)可写为：

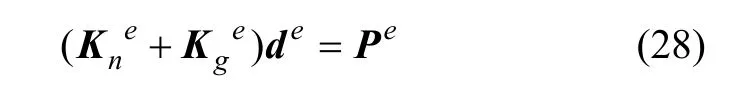
其中：

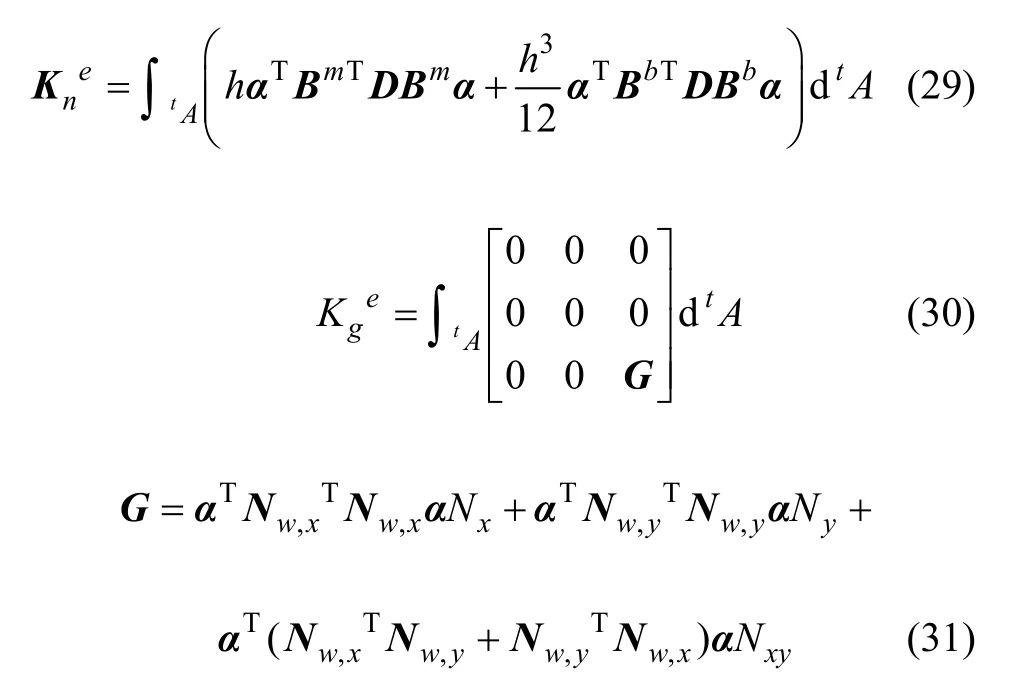
其中：h为单元厚度；Nx，Ny和Nxy为单元膜内力，由截面应力沿厚度方向积分得到；为单元自然变形刚度矩阵；当假定单元为完全弹性时，D为线弹性本构关系矩阵，当考虑材料弹塑性影响时，D则是切线本构关系矩阵。为单元几何刚度矩阵，反映单元变形对初始节点力的影响。de和Pe分别为节点位移和等效节点外荷载。

2 板壳结构非线性分析

基于经典Updated-Lagrange列式的板壳结构非线性响应分析一般采用增量-迭代求解技术[15]。主要思路是将施加在结构上外荷载(或某些关键点的位移)分成离散的增量步以避免处理大位移、大转动以及考虑材料塑性等问题带来的不便，随后根据弧长法等平衡路径追踪策略，形成自动增量累加系统。为了求得典型增量步内结构响应(内力和变形)需要引入迭代策略，这是由问题的非线性本质所决定的。结构非线性分析的核心是基于平衡迭代寻求结构非线性响应，故上述增量-迭代方法的关键落在典型增量步内平衡迭代上。一般来说，非线性迭代过程可分成3个阶段：预测阶段、修正阶段和平衡校核阶段。为了全文叙述完整，下面简要描述这3个阶段：

(1) 预测阶段，首先依据初始几何和物理条件，按式(29)和(30)计算单元切线刚度矩阵，又由“对号入座”法则组拼结构整体切线刚度矩阵和结构整体荷载列阵；其次，求解线性方程组得到节点位移预测值

3 数值算例

算例1 受弯方板弹塑性分析

本算例旨在说明本文提出的四节点平板壳单元可以较好地模拟塑性变形逐步发展的过程。如图 2(a)所示，承受均布荷载 q作用的四边简支方形板的边长L=1.0 m，板厚h=0.01 m，板件用材的弹性模量E=10.92 kPa，泊松比μ=0.3，屈服极限s=1 600 kPa。Owen和Hinton[16]采用 2×2的 9节点 Largrange单元和Heterosis单元网格划分1/4板面积，运用截面分层法考虑塑性沿板厚的开展，最终得到板的极限荷载因子25.0。Voyiadjis等[17]计算了板的荷载-中央挠度曲线，如图2(b)所示。为了便于比较，本文利用对称性将1/4方板划分成4×4的网格，计算方板的荷载-变位曲线(如图2(b)所示)，并得到板的极限荷载因子为24.943。可见，本文计算结果与文献[16]和[17]的结果吻合。

算例2 圆柱壳屋顶空间大变形分析

如图 3(a)所示，两对边简支的圆柱壳屋顶承受中央竖向集中力P的作用。柱壳屋顶的厚度为12.7 mm。该算例也是分析结构空间几何非线性分析的经典考题，不少学者给出各自分析结果[18-19]。屋顶的材料特性参数：E=3.102 75×103MPa，μ=0.3，几何参数屋面圆弧半径R=2.54 m，L=0.254 m，θ=0.1 rad。出于对称性考虑，只取1/4的屋顶进行分析，采用8×8单元网格模式。计算结果如图3(b)所示，可见用8×8网格分析12.7 mm厚屋顶可以满足工程计算精度需要。进一步说明采用本文提出的带面内自旋自由度四节点平板壳单元分析板壳结构非线性问题具有较高的计算精度和求解效率。

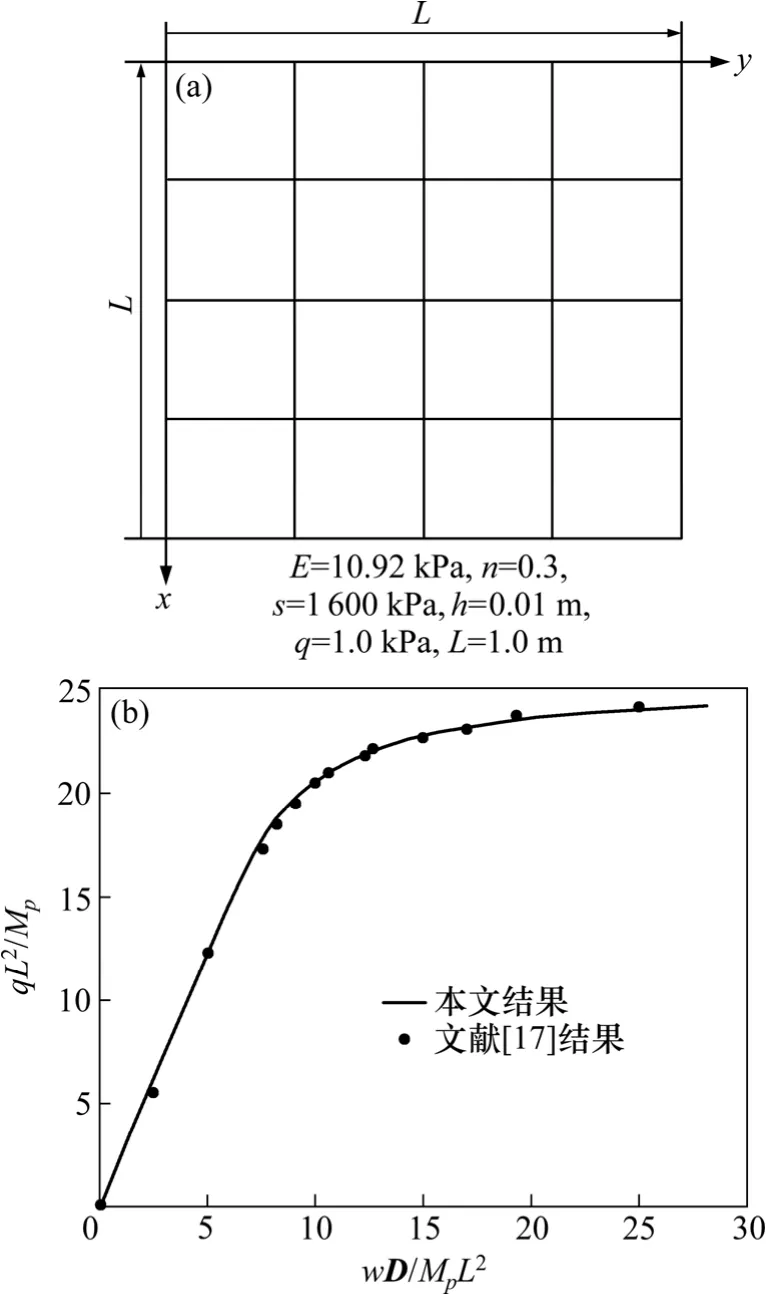
图2 四边简支矩形板荷载-中央挠度曲线Fig. 2 Load-deflection curve of simply-supported square plate

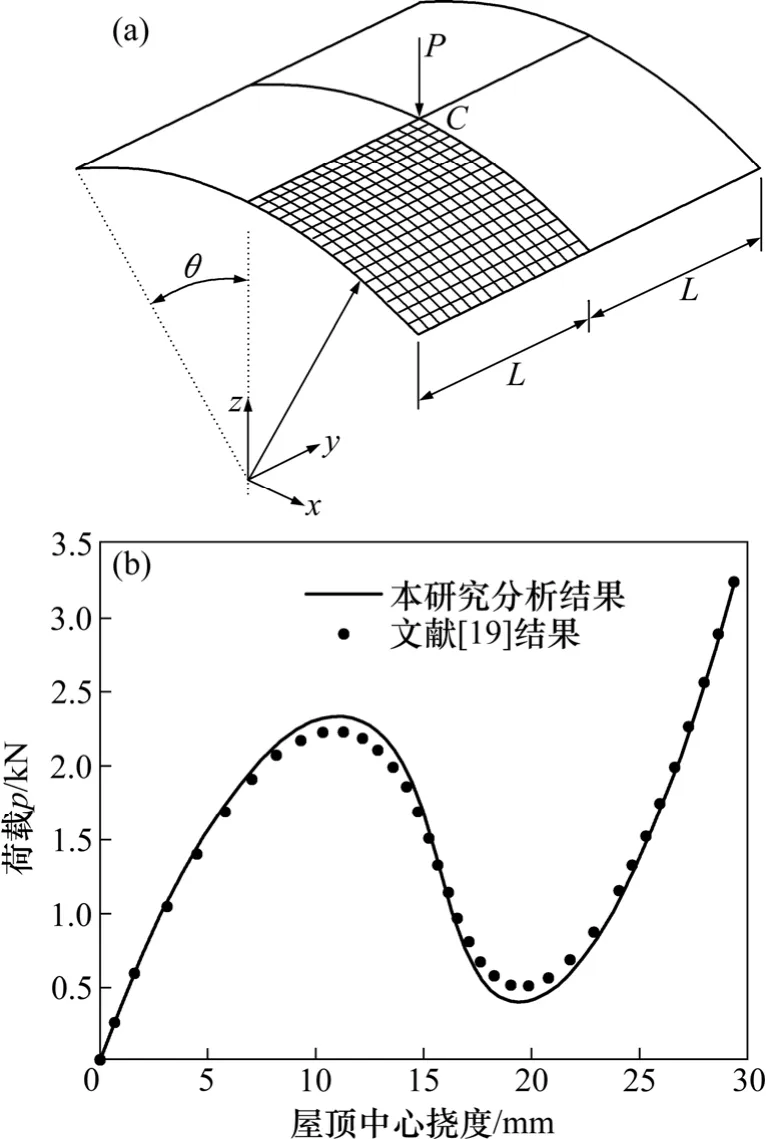
图3 圆柱壳屋顶空间大变位分析Fig. 3 Large deflection analysis of cylindrical roof under a central point load

4 结论

(1) 提出了一种引入面内自旋自由度的四节点平板壳单元。通过给定单元纵、横向条带位移模式进而确定单元位移场。此种基于“条带”的位移模型既能保证相邻单元边界线位移与转角的协调一致又能与梁单元较好耦合(例如模拟带肋板壳结构)。引入节点面内转动自由度既能避免壳元共面后结构整体刚度矩阵奇异又可改善壳元面内刚度“过刚”而导致的薄膜闭锁。

(2) 依据经典有限单元法例程，推导了四节点平板壳单元的小变形(自然变形)刚度矩阵和几何刚度矩阵的计算表达式。推导思路清晰，过程简洁，便于工程应用。

(3) 2个算例的数值结果表明：构造四节点平板壳单元不仅物理概念明确而且用于有限元分析计算结果正确、可靠。在分析一般板壳结构时，用较粗略的网格可以获得满足工程精度要求的结果。

[1] Hinton E, Owen D R J. Finite element software for plates and shells[M]. Swansea: Pineridge Press, 1984: 157-176.

[2] Cook R D, Malkus D S,Plesha M E, et al. Concepts and applications of finite element analysis[M]. 4th ed. New York:John & Wiley Sons, 2002: 530-580.

[3] 龙驭球, 龙志飞, 岑松. 新型有限元论[M]. 北京: 清华大学出版社, 2005: 5-7.LONG Yuqiu, LONG Zhi-fei, CENG Song. Advanced finite element method in structural engineering[M]. Beijing: Tsinghua University Press, 2005: 5-7.

[4] Hughes T J R, Brezzi F. On drilling degrees of freedom[J].Computer Methods in Applied Mechanics and Engineering, 1989,72(1): 105-121.

[5] Allman D J. A quadrilateral finite element including vertex rotations for plane elasticity analysis[J]. International Journal for Numerical Methods in Engineering, 1988, 26(3): 717-730.

[6] 朱菊芬, 郑罡. 带旋转自由度C0类任意四边形板(壳)单元[J].计算力学学报, 2000, 17(3): 287-292.ZHU Jufen, ZHENG Gang. A new 4-node C0 quadrilateral plate/shell element with drilling degree of freedom[J]. Chinese Journal of Computational Mechanics, 2000, 17(3): 287-292.

[7] LONG Yuqiu, XU Yin. Generalized conforming triangular membrane element with vertex rigid rotational freedoms[J].Finite Elements in Analysis and Design, 1994, 17(4): 259-271.

[8] 冯仲齐, 梅占馨. 有旋转自由度的高精度四边形单元 [J]. 应用力学学报, 2002, 19(1): 119-123.FENG Zhongqi, MEI Zhanxin. A high precision quadrilateral element with rotational degree of freedom[J]. Chinese Journal of Applied Mechanics, 2002, 19(1): 119-123.

[9] 夏桂云, 曾庆元, 李传习. 用有限条带构造带旋转自由度的矩形膜元[J]. 长沙交通学院学报, 2005, 21(1): 16-20.XIA Guiyun, ZENG Qingyuan, LI Chuanxi. A rectangular membrane element with rotational degree of freedom consisted of finite belts[J]. Journal of Changsha Communications University, 2005, 21(1): 16-20.

[10] 康澜, 张其林. 带旋转自由度的四边形平板壳单元[J]. 同济大学学报: 自然科学版, 2009, 37(2): 164-168.KANG Lan, ZHANG Qilin. A quadrilateral flat shell element with drilling degree of freedom[J]. Journal of Tongji University:Natural Science, 2009, 37(2): 164-168.

[11] Przemieniecki J S. Theory of matrix structural analysis[M]. New York: Dover Publication, 1985: 121-122.

[12] 王勖成, 邵敏. 有限单元波基本原理和数值方法[M]. 第2版.北京: 清华大学出版社, 1996: 329-334.WANG Xucheng, SHAO Min. Principles and numerical methods of finitie element methods[M]. 2nd ed. Beijing: Tsinghua University Press, 1996: 329-334.

[13] 王荣辉. 杆、板、壳结构计算理论及应用[M]. 北京: 中国铁道出版社, 1999: 237-239.WANG Ronghui. Bars, plates and shells: Theory and applications[M]. Beijing: China Railway Publishing House,1999: 237-239.

[14] Bathe K J. Finite element procedure[M]. New York:Prentice-Hall, 1996: 522-528.

[15] Riks E. An incremental approach to the solution of snapping buckling problems[J]. International Journal of Solids and Structures, 1979, 15(7): 529-551.

[16] Owen D R J, Hinton E. Finite elements in plasticity: Theory and practice[M]. Swansea: Pineridge Press, 1980: 370-371.

[17] Voyiadjis G Z, Woelke P. General non-linear finite element analysis of thick plates and shells[J]. International Journal of Solids and Structures, 2006, 43(7/8): 2209-2242.

[18] Yang Y B, Chang J T, Yao J D. A simple nonlinear triangular plate element and strategies of computation for nonlinear analysis[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 178(3/4): 307-321.

[19] Sze K Y, Liu X H, Lo S H. Popular benchmark problems for geometric nonlinear analysis of shells[J]. Finite Elements in Analysis and Design, 2004, 40(11): 1551-1569.