动力锂离子电池充电过程热模拟及影响因素灰色关联分析
鄂加强 ,龙艳平,王曙辉 ,蔡皓 ,胡小峰,朱蓉甲
(1. 湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙,410082;2. 湖南大学 机械与运载工程学院,湖南 长沙,410082)
动力锂离子电池具有能量密度高、使用寿命长、额定电压高、功率承受力高和自放电率低等优点,成为混合动力汽车和电动汽车的理想动力电池,但是,锂离子电池的安全问题成为阻碍其广泛应用于动力领域的主要因素。解决锂离子电池安全问题的首要任务是掌握锂离子电池内部的产热机理和热场分布。国内外关于锂离子电池的工作特性及安全性能研究主要包括:(1) 电池在放电过程中,放电速率、热交换、热辐射等对电池表面温度分布的影响[1];(2) 电池结构对电池散热的影响[2];(3) 滥用情况下动力用锂离子电池内部温度场的模拟[3];(4) 短路实验中电化学反应与电池热稳定之间的的关系[4];(5) 动力用锂离子电池电解液对电池散热的抑制因子[5];(6) 不同正极材料对动力用锂离子电池正、负极熵变化的影响以及熵变化对电池温度的影响[6];(7) 放电电流、对流换热条件及热辐射对电池熵及表面温度分布的影响[7];(8) 动力用锂离子电池在高频率脉冲电压充电工况下的热行为[8];(9) HEV和EV锂离子电池的产热量及电池充放电过程中的热平衡[9];(10) 动力用锂离子电池产热机理的研究[10]。这些研究和分析或者基于二维模型,或者忽略动力用锂离子电池内部分层结构的三维模型,有些还只是研究单一因素对电池内部温度场或者电池表面温度的影响,并没有明确各因素对动力用锂离子电池热行为的影响程度。动力用锂离子电池内部温度场不仅受电池内部各产热因素的影响,而且受电池散热因素的影响[11]。为此,本文作者建立动力用锂离子电池三维模型,对影响其内部温度场的产热因素(充电电流)和散热因素(电池外部环境温度、对流传热系数、辐射系数等)进行分析,并采用灰色关联分析方法对影响动力用锂离子电池内部温度场的各个因素进行评价分析。
1 动力用锂离子电池热模型
1.1 动力锂离子电池工作原理
选最常用的锰系圆柱形动力锂离子电池为研究对象。电池外观尺寸(直径×高)为50 mm×200 mm,容量为 22 A·h,图1所示为其在Gambit中划分网格后的三维模型。
动力用锂离子电池的电化学反应方程式如下。


图1 动力锂离子电池结构及网格图Fig.1 of model geometry and computational mesh
本文所选动力用锂离子电池的物理参数如表1所示,其中:ρ为密度(kg/m3);c为比热容(J/(kg·K));k为导热系数(W/(m·K))。
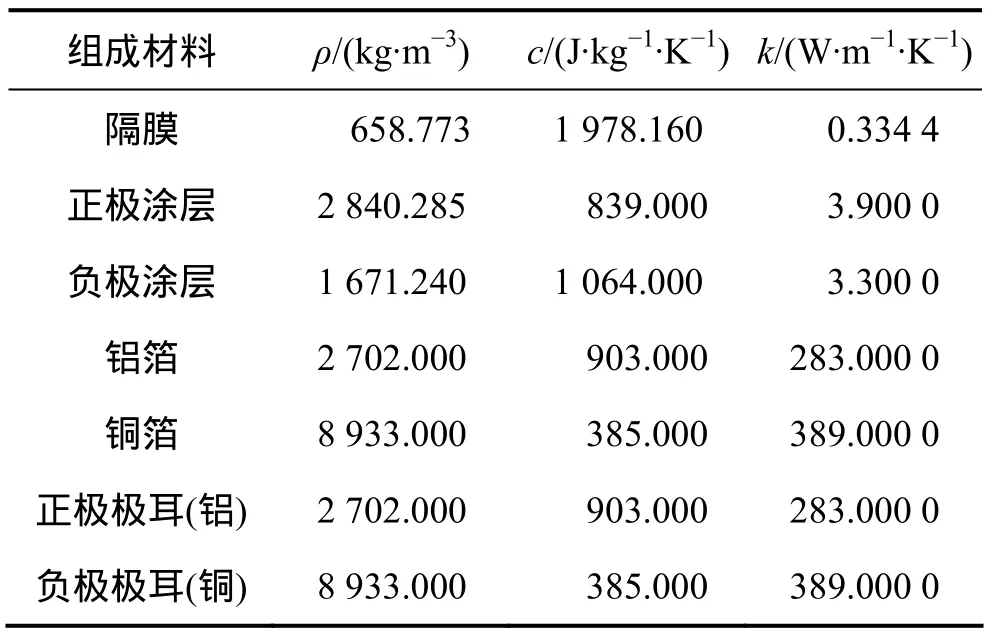
表1 锂离子电池物性参数Table 1 Physical properties of lithium ion battery
1.2 动力锂离子电池三维热模型建立
为减少计算量,忽略电池内部分层结构,但适当考虑电池内部各向异性的特点。同时,电池内部本是螺旋卷心,并非对称结构,但为了简化模型,将电池简化为对称结构,并且认为电池内部的温度传递也是轴对称的。
以动力锂离子电池内某处所在的微元体建立动力锂离子电池三维热模拟模型,并确定相应的初始条件和边界条件。
(1) 能量方程为

式中:ρ为动力用锂离子电池内某处密度(kg/m3),取电池的加权平均密度;kr和kh分别为径向和轴向导热率,kp,kn和 ks分别为正极、负极和隔膜的平均热导率;r为电池半径;h为电池高度;rp,rn和rs分别为径向正极、负极和隔膜的总厚度; hp,hn和hs分别为轴向正极、负极和隔膜的总厚度;q为动力用锂离子电池内某处单位体积热生产率(W/m3);T为动力用锂离子电池内某处热力学温度(K);∇为梯度算符,
动力用锂离子电池充电过程中,单位体积热产生速率q可表示为
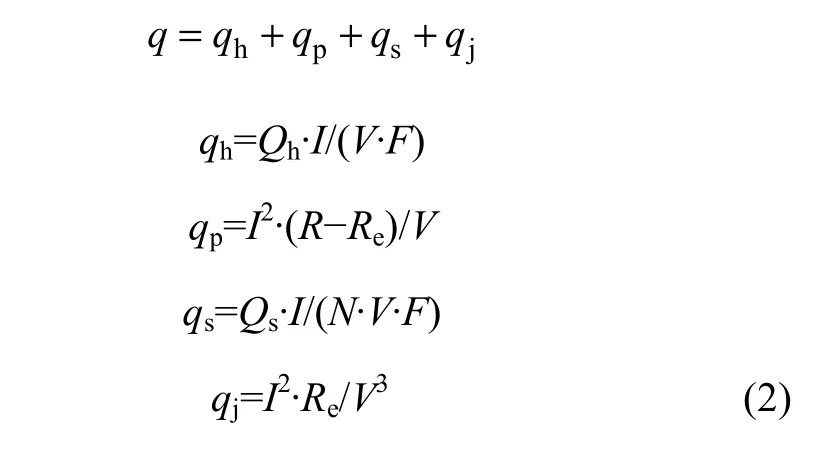
式中:qh为动力用锂离子电池电化学反应放热(W/m3);qp为动力用锂离子电池反应存在的极化热(W/m3);qs为动力用锂离子电池的副反应热(W/m3);qj为动力用锂离子电池电阻产生的焦耳热(W/m3);Qh为动力用锂离子电池的反应热(J/mol);I为电流(A);V为动力用锂离子电池单体体积(m3);F为法拉第常数(C/mol);R为动力用锂离子电池总内阻(Ω);Re为动力用锂离子电池纯电阻(Ω);Qs为动力用锂离子电池副反应热;N为电动势为E时动力用锂离子电池向外电路释放电子的物质的量(mol)。通过吉普斯自由能表达式ΔGf=ΣΔGi(生成物)-ΣΔGi(反应物)可得出 Qh和 Qs。热源的解析在fluent软件的UDF中实现。
(2) 初始条件:初始温度为 300 K,初始内阻为200 mΩ。
(3) 边界条件:在边界处,对流传热和热辐射都需考虑。对流传热方程为

式中:QC为对流换热量(J);α为对流换热系数;Ts为表面热力学温度(K);∞T为环境热力学温度(K)。
辐射传热方程为

式中:QR为热辐射换热量(J);ε为系统与环境交界处的热辐射系数;σ为 Stefan-Boltzmann常数,σ=5.67×10-8W/(m2·K4);TA为系统与环境交界处热力学温度(K)。
1.3 动力用锂离子电池热模拟结果与讨论
热模拟综合考虑了电池产热因素和散热因素。除电池本身的制造工艺及组成材料和结构特性在很大程度上决定了动力锂离子电池的热行为特性外,动力锂离子电池在工作过程中所处工况及环境也对电池的热行为有重要影响。对于某一特定的电池,充电电流为主要可控产热因素;电池与环境的对流换热、热辐射以及环境温度为可控散热因素。典型模拟工况有以下3点:(Ⅰ) 环境温度 T0=300 K,对流传热系数 α=75 W(m2·K),热辐射系数 ε=0.25时不同充电电流I对电池热行为的影响;(Ⅱ) 充电电流I=1C,对流传热系数α=75 W/(m2·K),热辐射系数 ε=0.25 时不同环境温度T0对电池热行为的影响;(Ⅲ) 充电电流I=1C,环境温度T0=300 K时,不同对流换热系数α和热辐射系数ε对电池热行为的影响等。

图2 工况Ⅰ中,充电电流为1C时电池内部温度场变化Fig.2 Temperature variation inside battery during charging with charge current of 1C under working condition Ⅰ
图2所示为电池在充电工况Ⅰ下,充电电流为1C时电池温度分布变化。从图2 (a)可以看出:在充电初始阶段,电池极端即极耳附近的温度比其他地方的温度高,这与电池内部电流密度分布有很大关系;在靠近极耳附近,电池极片上的电流密度较大,所以,产热速率比电流密度低的地方大;随着充电过程的进行,高温区逐渐从极耳附近向电池中心区域移动,这与电池外表的散热因素有关,且与电池极端的导热效应亦有很大关系;电池表面的对流换热能较快地将积聚在电池内部的热量散出,同时,由于电池正极端材料是铝,负极端材料是铜,这2种材料有很好的导热作用,能有效地将其附近的热量导出,所以,本来容易成为高温区的极耳附近区域温度上升速率渐渐降低,直至产热率和散热率达到平衡后,此处温度不再上升;而在电池内部,愈靠近中心地区,热量愈不易散出;而靠近电池壳体的区域,热量容易散出,这使电池内部温度达到稳定状态时,温度从内至外成梯状分布。从图2可以看出:电池内部的温度场呈现出温度在轴向方向的递减梯度明显大于径向方向的递减梯度,这是因为电池卷芯在轴向方法的导热率比径向方向的导热率大。从图 2(f)可以看出:当电池充电完毕时,电池内部温度达到整个充电过程中的最高值,且电池内部中心处温度达到近323 K,是整个电池温度最高区域,电池壳体两端边缘处的温度最低,约为318 K。电池外壳上的温度分布特点表明:在电池散热管理时,电池体中部可适当加大散热力度。
图3所示为工况Ⅰ下,充电完毕后电池内部温度分布;图4所示为不同充电过程中电池内部最高温度变化曲线。从图3(a)可以看出:用0.5C(C为充放电倍率)电流充电完毕时,电池内部最高温度可达到约316 K,最低温度约为311 K,且电池单体的温度场在充电大约2 000 s时达到了稳定状态。从图3(b)及图4中曲线2可以看出:充电完毕后电池内部最高温度达到323 K,最低温度约为318 K,在充电前1 500 s左右,电池内部升温速率很快,之后,温度上升速率较为平稳;电池以1.5C电流充电时,电池充电完毕后最高温度达到约335 K,在整个充电过程中,电池内部升温速率都很快,在充电前期更加明显。综合图3和图4可以看出:随着充电电流的逐渐增大,电池充电过程中的升温速率逐渐增大且电池内部温度相应增高。这是因为电池在充电过程中的各个热源产热率都与电流有密切联系,过大的充电电流会使电池内部的热量迅速积累,而使温度上升速率加快;当动力用锂离子充电电流继续增大时,可导致电池温度过高而失效甚至爆炸,所以,要控制动力用锂离子电池的充电电流。

图3 工况Ⅰ中,不同充电电流下充电完毕后电池内部温度分布Fig.3 Temperature distribution with different charge currents after charge under working condition Ⅰ

图4 工况Ⅰ中,电池在不同充电电流充电过程中内部最高温度变化Fig.4 Temperature variation inside battery charge currents with different charge currents under working condition Ⅰ
图5所示为电池在工况Ⅱ下的温度分布,图6所示为相应工况下电池充电过程中温度变化曲线。
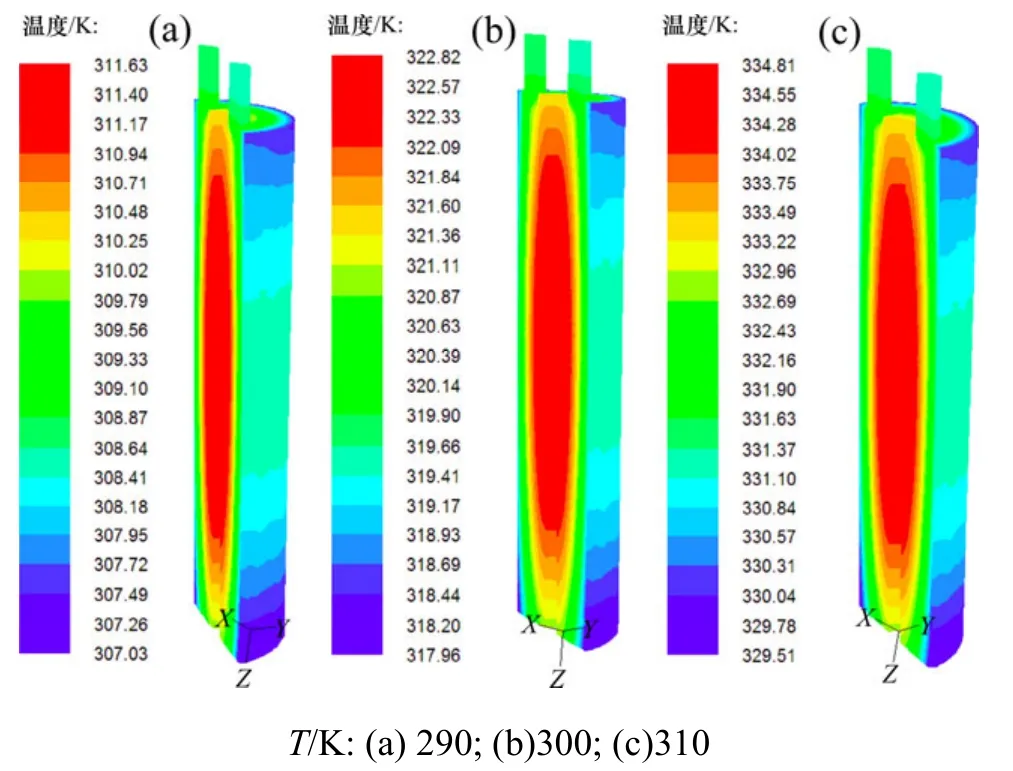
图5 工况Ⅱ中,不同环境温度下充电完毕后电池内部温度分布Fig.5 Temperature distribution after charge in different ambient temperatures under working conditionⅡ
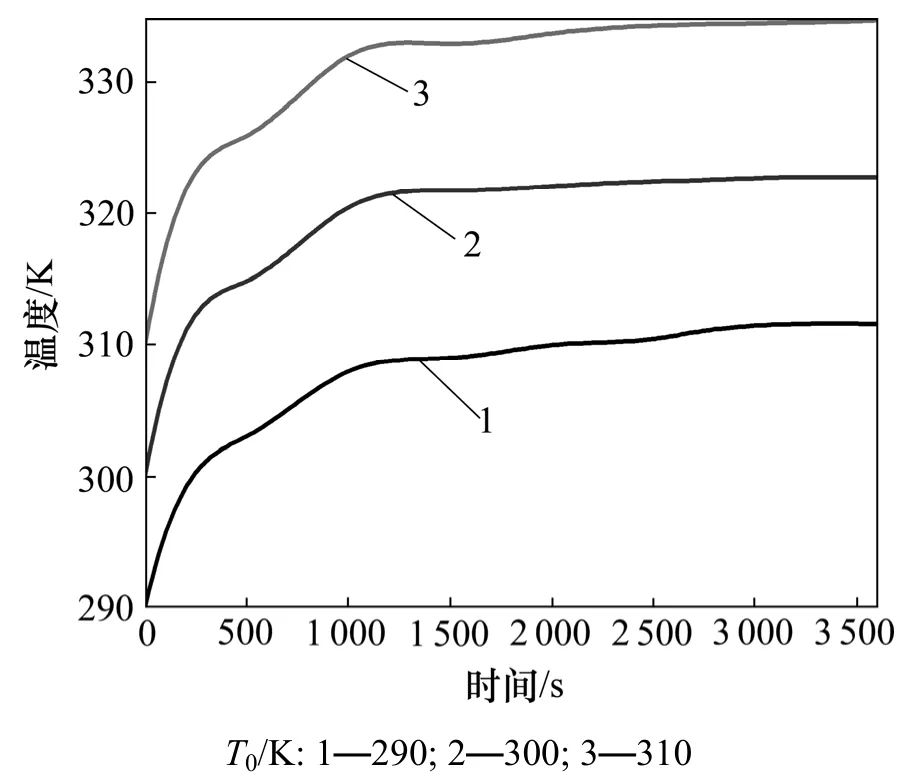
图6 工况Ⅱ中,不同环境温度下电池充电过程中内部最高温度变化Fig.6 The maximum temperature variation in different ambient temperatures under working conditionⅡ
从图5和图6可以看出:电池在相同充电电流和散热条件下,环境温度越高,电池内部最高温度越高;在环境温度从290 K至335 K变化范围内,电池最高温度约从311 K变化至335 K。这段环境温度对电池的升温速率影响不大,它使动力用锂离子电池温度升高,主要表现在抑制动力用锂离子电池的散热上。

图7 工况Ⅲ中,α=7 W/(m2·K)时充电完毕后电池内部温度分布Fig.7 Temperature distribution after charge and coefficient of heat transfer of α=7 W/(m2·K) with different thermal radiation coefficients under working condition Ⅲ
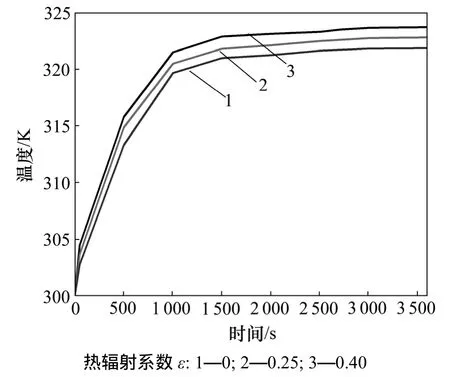
图8 工况Ⅲ中,对流换热系数为75 W/(m2·K),不同热辐射系数下电池充电过程中内部最高温度变化Fig.8 Temperature variation inside battery when coefficient of heat transfer is 75 W/(m2·K) in different thermal radiation coefficient under working condition Ⅲ
工况Ⅲ中,α不同时电池内部温度分布见图7~10。从图7~10可以看出:当对流换热系数为75 W/(m2·K)(强制换热)时,辐射系数的变化对电池内部最高温度的影响不大;而在对流换热系数为7 W/(m2·K)时,热辐射对电池温度的影响明显增大。这是因为在较高的换热系数下,电池散热效果良好,电池的表面温度温度较低,而辐射传热与系统表面温度的4次方与环境温度的4次方之差成正比,电池表面温度越低,辐射换热的效果就越不明显。从图10可看出:在充电后期,电池内部升温速率陡增,这是由电池内部瞬间产热量增大所致;当电池内部温度超过 80 ℃时[12],电池内部开始出现了副反应,这些副反应放出大量热,使得电池内部热量的积累迅速上升,从而出现了峰值。

图9 工况Ⅲ中,α=75 W/(m·K)、时间为时8 000 s时电池内部温度分布Fig.9 Temperature distribution after charge and coefficient of heat transfer of 75 W/(m·K) with different thermal radiation coefficients under working condition Ⅲ
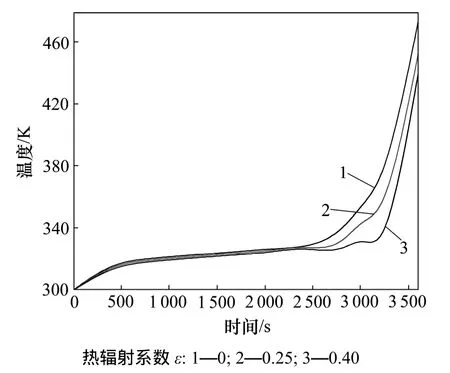
图10 工况Ⅲ中,对流换热系数为7 W/(m2·K)时,不同热辐射系数ε下电池充电过程中内部最高温度变化Fig.10 The maximum temperature variation inside battery when coefficient of heat transfer is 7 W/(m2·K) in different thermal radiation coefficient under working condition Ⅲ
图9和图10表明:动力用锂离子电池表面的热辐射可发挥一定的散热作用,能对电池安全使用起一定保护作用。但若要确保动力锂离子电池正常工作,最有效的途径是对其实施强制散热。
通过以上分析可见:动力锂离子电池内部的热行为不仅与电池材料有密切关系,而且在很大程度上依赖于所处工况。充电电流对电池温度影响很大,并且电流越大,电池内部升温速率越快,所以,充电电流过大很容易造成电池内部热积累过多,从而影响电池性能,甚至破坏电池;电池所处环境温度对电池热行为影响也很大,对流换热对动力电池内部温度场的影响不可忽略,在自然对流情况下,电池温度上升很快,特别是热辐射很小的情况下,电池内部最高温度会达到引起内部化学反应的温度。在散热情况良好、电池温度不高的情况下,热辐射对电池内部温度的影响不明显,但是,在高温下有一定的影响。
2 动力用锂离子电池热因素灰色关联分析
2.1 灰色关联分析方法
灰色关联分析是对信息不完全的系统进行关度分析,计算各因素之间的相互影响程度[11-14]。本文用此方法评价动力锂离子电池热行为,基本思路及实现方法如下。
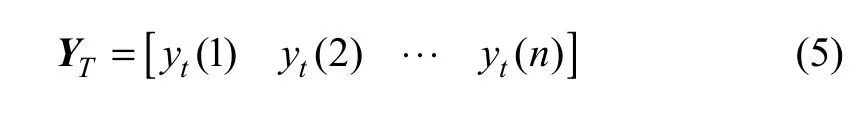
式中:YT表示第 T组参考序列;[yt(1) yt(2) … yt(n)]为YT组中参考序列中的数据。
设系统被研究的影响因素向量有m个,在这些因素影响下被研究的工况有n种,记其相应的特征向量矩阵为
(1) 设定参考序列及比较序列。参考序列是进行比较的“母序列”,记其特征向量矩阵为
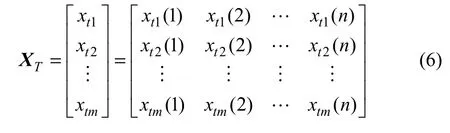
式中:XT为对应于参考序列YT的比较序列。
(2) 原始数列无量纲化。为减小分析识别的错误概率,在计算前,需要对各具有不同量纲的特征参数进行无量纲化,本文采用数据区间化无量纲化。
(3) 计算灰色关联系数。参考序列与各比较序列的仿真之差可用下列关联关系式表示:

式中:Δmin为参考序列 YT与比较序列 XT中对应元素的最小绝对差值,为分辨系数,ρ∈(0, 1),一般取0.1~0.5;Δmax为相应的最大绝对差值,
(4) 计算关联度。根据关联度系数可得出关联度:

2.2 应用实例
为研究影响动力锂离子电池热行为的因素,分别对不同对流传热系数 α、辐射系数 ε、环境温度 T0、充电电流I等工况下进行多次热模拟,解析动力锂离子电池内部最高温度T。表2所示为10种工况下充电20 min和充电结束时动力锂离子电池的模拟结果。
设在各工况下,充电20 min时动力锂离子电池内部的最高温度为参考序列Ya(k),各工况下充电完毕后动力锂离子电池内部的最高温度为参考序列Yb(k),并以对流换热系数矩阵 X1(k)、热辐射系数矩阵 X2(k)、环境温度矩阵 X3(k)、充电电流矩阵 X4(k)作为比较序列,以此研究各因素对电池内部热行为的影响程度。无量纲化后得到如下序列:
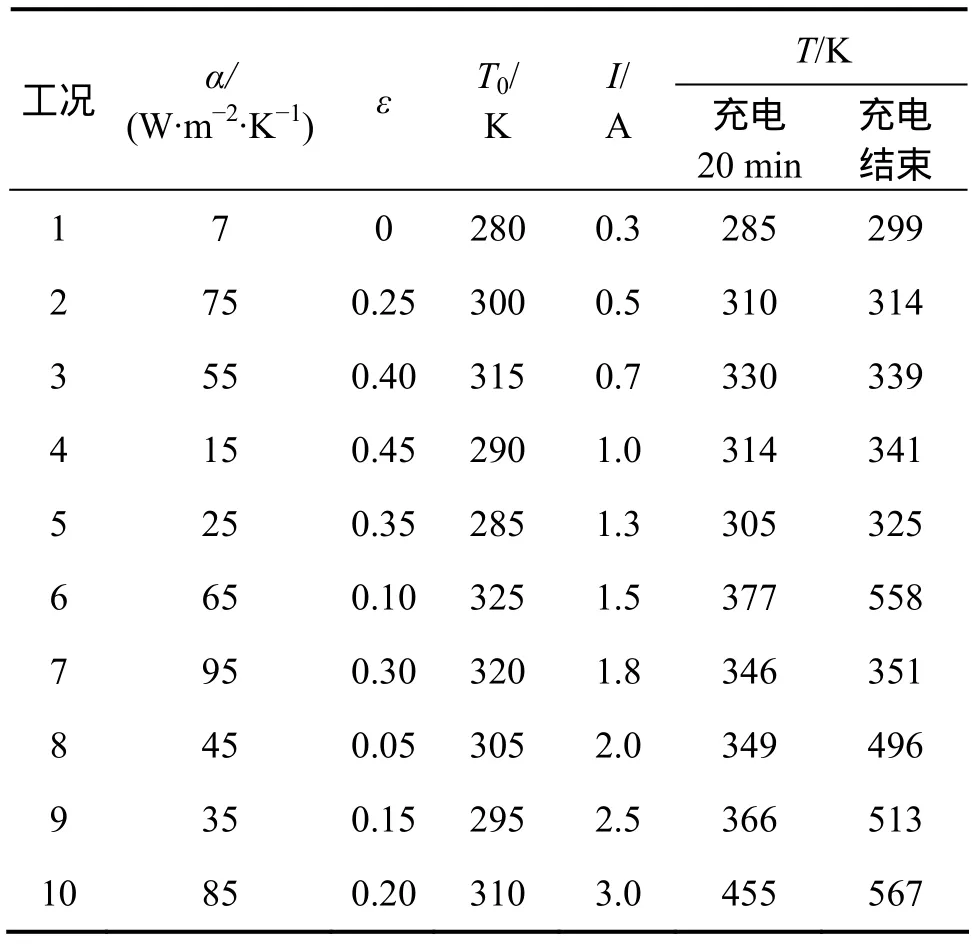
表2 充电20 min和充电结束时动力锂离子电池的热模拟结果Table 2 Simulated results of thermal behavior in dynamic lithium ion battery when being charged 20 min and at end of charge

充电20 min时多工况灰色关联系数矩阵:

充电完毕工况灰色关联系数矩阵为:

将以上计算结果代入式(8)~(9),可得各因素对动力用锂离子电池内部热行为影响的关联度,见表3。
从表3可以看出:在充电过程中,充电电流对电池内部温度的影响最大。充电电流是电池在充电过程中产热的根本原因,而环境温度和对流换热对电池内部温度的影响相当(关联度分别为 0.658 04和0.511 03)。这主要是因为对流换热实际上是通过降低电池表面温度即环境温度来降低电池内部温度,所以,环境温度和对流换热对电池内部温度的影响实质上是一样的,而热辐射对电池温度的影响最小。
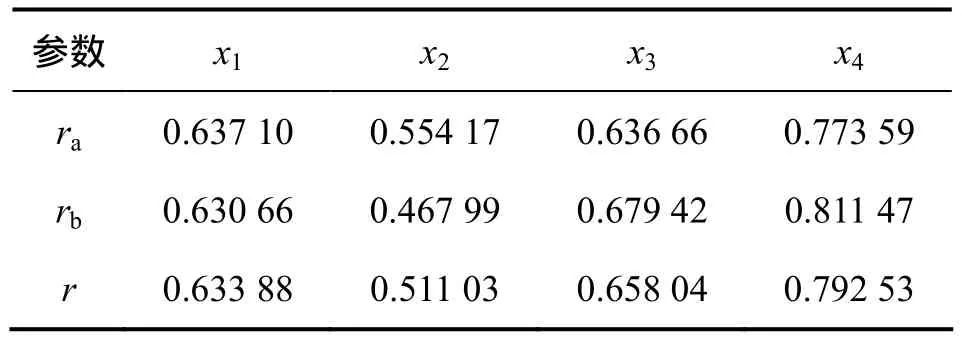
表3 动力锂离子电池热因素影响关联度Table 3 Grey relational degree of thermal factors of dynamic lithium-ion battery
3 结论
(1) 动力用锂离子电池内部最高温度随着电流的增大而增大,但动力用锂离子电池内部的升温速率先在充电电流增大的某个时段基本不变,随后也将随充电电流增大而增大。
(2) 环境温度越高,动力用锂离子电池充电完毕后,内部最高温度越高。降低环境温度是防止动力用锂离子电池内部温度过高的有效手段。
(3) 对流换热系数越大,则电池内部温度越低,所以,有效地散热是保证电池正常工作的必要措施。
(4) 强制换热时,辐射系数的变化对电池内部最高温度影响不大;而自然对流换热时,热辐射对内部最高温度影响明显。
(5) 充电电流I关联度(0.792 53)>环境温度T0关联度(0.658 0 4)>对流换热系数α关联度(0.633 88)>热辐射系数ε关联度(0.511 03)。
[1] Chen S C, Wan C C, Wang Y Y. Thermal analysis of lithium-ion batteries[J]. Power Source, 2005, 140: 111-124.
[2] 张遥, 白杨, 刘江兴. 动力用锂离子电池热仿真分析[J]. 电源技术, 2008, 32(7): 461-463.ZHANG Yao, BAI Yang, LIU Jiangxing. Simulation analysis on thermal behavior for power lithium-ion battery[J]. Chinese Journal of Power Sources, 2008, 32(7): 461-463.
[3] Kim G H, Pesaran A, Spotnitz R. A three-dimensional thermal abuse model for lithium-ion cells[J]. Journal of Power Source,2007, 170: 476-489.
[4] Wu M S, Chiang P C J, Lin J C, et al. Correlation between electrochemical characteristics and thermal stability of advanced lithium-ion batteries in abuse tests: Short-circuit tests[J].Electrochimica Acta, 2004, 49: 1803-1812.
[5] Mandal B K, Padhi A K, ZHONG Shi, et al. Thermal runaway inhibitors for lithium battery electrolytes[J]. Journal of Power Sources, 2006, 161: 1341-1345.
[6] Williford R E, Viswanathan V V, ZHANG Jiguang. Effects of entropy changes in anodes and cathodes on the thermal behavior of lithium ion batteries[J]. Journal of Power Sources, 2009, 189:101-107.
[7] Dong H J, Seung M B. Thermal modeling of cylindrical lithium ion battery during discharge cycle[J]. Energy Conversion and Management, 2011, 52: 2973-2981.
[8] Saito Y. Thermal behaviors of lithium-ion batteries during high-rate pulse cycling[J]. Journal of Power Sources, 2005, 146:770-774.
[9] Saito N. Thermal behavior analysis of lithium-ion batteries for electric and hybrid vehicles[J]. Power Source, 2001, 99: 70-77.
[10] 杨凯, 李大贺, 陈实, 等. 电动汽车动力电池的热效应模型[J].北京理工大学学报, 2008, 28(9): 782-785.YANG Kai, LI Dahe, CHEN Shi, et al. Thermal model of batteries for electrical vehicles[J]. Journal of Beijing Institute of Technology, 2008, 29(9): 782-785.
[11] 郭炳焜, 徐徽, 王先友. 锂离子电池[M]. 长沙: 中南大学出版社, 2002: 18-54.GOU Bingkun, XU Hui, WANG Xianyou. Lithium ion batteries[M]. Changsha: Central South University Press, 2002:18-54.
[12] 胡传跃, 李新海, 郭军, 等. 高温下锂离子电池电解液与电极的反应[J]. 中国有色金属学报, 2007, 17(4): 629-635.HU Chuanyue, LI Xinhai, GUO Jun, et al. Reactions between electrolyte and electrode of lithium ion batteries at elevated temperature[J]. The Chinese Journal of Nonferrous Metals, 2007,17(4): 629-635.
[13] Giuliano M R, Advani S G, Prasad A K.Thermal analysis and management of lithium–titanate batteries[J]. Journal of Power Sources, 2011, 196: 6517-6524.
[14] ZHANG Xiongwen. Thermal analysis of a cylindrical lithium-ion battery[J]. Electrochimica Acta, 2011, 56:1246-1255.
[15] 吴宇平, 戴晓兵. 锂离子电池应用与实践[M]. 北京: 化学工业出版社, 2004: 27-82.WU Yuping, DAI Xiaobing. Lithium ion battery application and practice[M]. Beijing: Chemical Industry Press, 2004: 27-82.
[16] 陈玉红, 唐致远, 卢星河, 等. 锂离子电池爆炸机理研究[J].化学进展, 2006, 18(6): 823-831.CHEN Yuhong, TANG Zhiyuan, LU Xinghe, et al. Research of explosion mechanism of lithium ion battery[J]. Progress in Chemistry, 2006, 18(6): 823-831.
[17] 刘思峰. 灰色系统理论及其应用[M]. 北京: 科学出版社,2010: 54-100.LIU Sifeng. Gray system theory and application[M]. Beijing:Science Press, 2010: 54-100.
[18] E Jiaqiang, LI Yuqiang, GONG Jinke. Function chain neural network prediction on heat transfer performance of oscillating heat pipe based on grey relational analysis[J]. Journal of Central South University of Technology, 2011, 18(5): 1733-1737.

