完全零单半群的某些性质

崔菊芬，张建刚

（上海师范大学数理学院，上海 200234）

完全零单半群的某些性质

崔菊芬，张建刚

（上海师范大学数理学院，上海 200234）

讨论了完全零单半群S的夹心阵P和结构群G的交换性对其性质的影响，推广了完全单半群中的相应结果，研究了当S中每个不含零的子带均为左零或者右零带时S中元素的特征，并进一步刻画了完全零单半群幂等元的逆元的分布情况.

完全零单半群；完全单半群；夹心矩阵

1 预备知识

众所周知，正则半群是半群代数理论的主要研究对象.完全零单半群是其中最基础的一个子类，它们在正则半群中起着重要的作用.因此，关于这类半群的研究一直受到许多人的重视.在1928年，俄国数学家СушкеВич系统地研究了特殊的完全零单半群——有限单半群的结构，可以看做是完全零单半群研究的开始.1940年，Rees.D讨论了任意完全零单半群的结构.Rees的结论由A.H.Clifford和G.B. Preston在其1961的专著中得到了简洁而优美的表述［1］，A.H.Clifford和G.B.Preston称之为Rees定理.

由Rees定理，每一个完全零单半群都同构于一个Rees矩阵半群M0［G；I，Λ；P］.通过对集合I，Λ的分类，可以得到Rees矩阵半群的非零块，并可证明它们是完全单子半群.进一步将讨论S夹心阵P和结构群G的交换性对S的性质的影响.在文章的第二部分分了3个层次讨论了S的性质.文章的第三部分讨论了完全零单半群与纯正相关的一些性质以及幂等元的逆元的分布情况.

定义1.1令S是一个半群，E(S）表示其幂等元集合.若e∈E(S），称e为本原幂等元，如果对任意的f∈E(S），

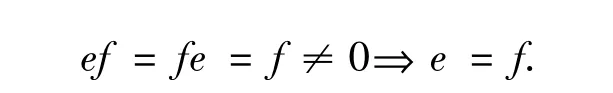
定义1.2一个含0的半群S叫做null半群，若S中任意两个元素的乘积是0.

定义1.3不含0的半群S是单的，若S没有真理想.含0的半群S叫做零单半群，若

(i）除｛0｝和本身之外不再有其他的理想；

(ii）S2≠｛0｝.

零单半群S称为完全零单半群，如果S含有一个本原幂等元.

令G为群，e是G的单位元，I，Λ是两个非空集合，令P＝(pλi）是一个Λ×I矩阵，其中元素取自于G0＝G∪｛0｝(称为G0上的Λ×I矩阵），满足：

即P中每行每列都有非零元(称P正则）.

令S＝(I×G×Λ）∪｛0｝，定义S上的运算“·”为：∀(i，a，λ），(j，b，u）∈S，

引理1.1［1］如上定义的S是一个完全零单半群，记为S＝M0［G；I，Λ；P］.反之，每个完全零单半群都可以如此构造.特别的，若矩阵P中元素均为群G的元素，元素运算定义为：

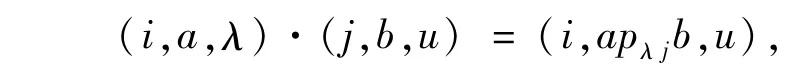
则S＼｛0｝是一个完全单半群，记作S＝M［G；I，Λ；P］.反之，每个完全单半群都可以如此构造.

令S＝M0［G；I，Λ；P］是一个完全零单半群.其中矩阵P称为完全零单半群S的夹心阵.对每一个i∈I，记Λi＝｛λ∈Λ：pλi≠0｝；对每一个λ∈Λ，记Iλ＝｛i∈I：pλi≠0｝.设εI和εΛ分别为I和Λ上的等价关系.它们的定义如下：

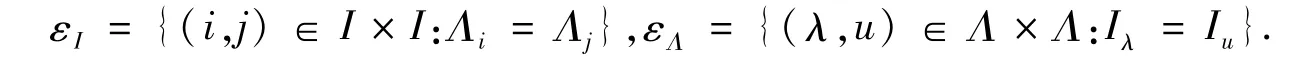
记包含i的εI类为i*，包含λ的εΛ类为λ*.由εI和εΛ的定义可知，矩阵P＝(pλi）被分成若干个子块i*×λ*，并且对所有的i∈i*和λ∈λ*，要么pλi＝ 0，要么pλi≠0.

定义1.4对所有的i∈i*，λ∈λ*，都有pλi≠0.则称i*×λ*是夹心矩阵P的一个非零块.反之称为零块.

矩阵P的正则性可以保证对于每一个i*，均存在λ*使得i*×λ*是非零块.

令S是一个半群，元素a∈S称为正则的，如果存在x∈S使得a＝axa，若S中每个元素均正则，则称S是一个正则半群.完全(零）单半群是正则半群.S的幂等元集合记作E(S）.正则半群称为纯正的，若E(S）是子半群.对任意的a∈S，如存在x∈S使得a＝axa，x＝xax，称x为a的逆元，记a的逆元集合为V(a）.令S是一个半群，定义其上的如下关系，称作格林关系.

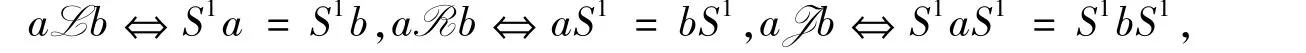
且H＝R∩L，D＝L R.令a∈S，P为S上的格林关系，Pa表示a所在的P类.

文中未定义的术语和结论，请参看文献［2］，［3］.

2 完全零单半群中结构群G的交换性对S的影响

若一个半群S有如下性质，对于S中的任意元素x，y，都有xy＝yx，称半群S是交换半群(或阿贝尔半群）.设S是一个正则半群，E(S）表示其幂等元集合，则由E(S）生成的子半群＜E(S）＞称为S的核，记作C(S）.在这一部分主要讨论完全零单半群中的非零块随着夹心阵P和结构群G交换性而产生的变化.假定Rees矩阵半群S＝M0［G；I，Λ；P］，e是群G的单位元.从P中的元素是可交换的、P包含在G的中心、G是阿贝尔的这3个层面来讨论S非零块的性质.

引理2.1［3］令完全单半群S＝M0［G；I，Λ；P］，

(1）对任意的a≠ 0，La＝Sa＼｛0｝，Ra＝aS＼｛0｝.

(2）S是正则半群，且仅有两个D类，分别为｛0｝和D＝S＼｛0｝.如果a，b∈D，则或者ab＝ 0，或者ab∈Ra∩Lb，后者发生当且仅当La∩Rb包含有一个幂等元.

令(0≠）a＝(i，g，λ）∈S，由引理2. 1，结合Rees矩阵半群的运算，可以记La＝Lλ，Ra＝Ri.进而Ha＝La∩Ra＝Lλ∩Ri＝Hiλ.容易理解，Hiλ是一个群，当且仅当pλi≠ 0，且此时该群H类的幂等元为(i，是夹心矩阵P的一个非零块，即对所有的i∈i*，λ∈λ*，都有pλi≠ 0，记Si*×λ*＝∪｛Hiλ：i∈i*，λ∈λ*｝.很显然Si*×λ*是一些群的并.相应的称Si*×λ*是完全零单半群S的非零块，类似的，可以定义完全零单半群S的零块.对完全零单半群S的每一个H类必属于某一个零块或非零块.

定理2.1设S为完全零单半群.则S每一个非零块构成S的完全单子半群；S的每个零块和0构成S的null子半群.

证明不失一般性，设

若Si1*×λ3*构成S一个非零块.则对于任意的有pλi≠0成立，且Hiλ为群H类.由引理2.1(1），Hi1λ3，Hi1λ4在同一个R中，从而Hi1λ3∪Hi1λ4构成子半群，同理可以证明，Hi2λ3∪Hi2λ4，Hi1λ3∪Hi2λ3，Hi1λ4∪Hi2λ4构成子半群.任意的a∈Hi1λ3，b∈Hi2λ4，由于pλ 4，i2≠ 0，由引理2.1(2），ab∈Hi1λ4⊂eq Si1*×λ3*，从而Si1*×λ3*构成子半群.又因为Si1*×λ3*仅有一个D类，所以它是S的一个完全单子半群.

若Si1*×λ3*构成S的一个零块.则对于任意的i∈，λ∈，有pλi＝0成立.对任意的a，b∈Hiλ，由引理2.1(2），ab＝0.对任意的，由引理2.1 (2），ab＝0.从而，S的每一个零块添零后均为S的一个null子半群.定理证毕.

以下讨论P，G中元素的交换性对完全零单半群S的影响.完全单半群S称为过阿贝尔的，如果对任意的e∈E(S），He为阿贝尔群.

引理2.2［2］对于完全单半群S＝M［G；I，Λ；P］，若P中的元素是可交换的，则S满足恒等式ax0a0y0a＝ay0a0x0a.

定理2.2若P中的元素是可交换的，则对S的每一个非零块Si*×λ*，

(1）C(Si*×λ*）是过阿贝尔的.

(2）对任意的e，f，g，h∈E(Si*×λ*），若ef H gh，则有efgh＝ghef.

(3）Si*×λ*作为S的完全单子半群满足恒等式ax0a0y0a＝ay0a0x0a.

证明(1）设e1，…，em，f1，…，fn∈E(Si*×λ*），则e1…em，f1…fn∈C(Si*×λ*）.若e1…emH f1…fn，为方便，不妨取由完全零单半群的乘法及假设条件可知道，i＝k，u＝θ.不妨假设：

其中a，b均为P中元素或者P中元素作为群G的子群＜P＞中元素的逆元的乘积.由条件P中的元素是可交换，进而，P中的元素与子群＜P＞中元素的也交换，从而P中的元素与a，b都交换，故

所以C(Si）是过阿贝尔的.

(2）由(1）容易得到.(3）由引理2.2可得.

完全单半群称为中心的，如果任意两个幂等元的乘积落在其所在最大子群的中心里面.

引理2.3［2］对于完全单半群S＝M［G；I，Λ；P］，若P属于是G的中心，则S满足恒等式a0x0a＝ax0a0.

定理2.3若P属于是G的中心，则对S的每一个非零块Si*×λ*，

(1）Si*×λ*是中心的.

(2）Si*×λ*作为S的完全单子半群满足恒等式a0x0a＝ax0a0.

证明(1）对任意的u）.显然Hiμ是包含ef的极大子群.

对任意的a＝(i，g，u）∈Hef，因为P是G的中心，

故ef落在包含它的极大子群的中心里面.由e，f的任意性，得证.

(2）由(1）及引理2.3可得.

引理2.4［2］对于完全单半群S＝M［G；I，Λ；P］，若G是阿贝尔的，则S满足恒等式a0xa＝axa0.

定理2.4若G是阿贝尔的，则对S中任意的非零块Si*×λ*，

(1）Si*×λ*是过阿贝尔的.

(2）Si*×λ*作为S的完全单子半群满足恒等式a0xa＝axa0.

证明 (1）Si*×λ*是S的完全单子半群，且它的结构群也为G.完全单半群的每一个H类都同构与G，由于G阿贝尔的，所以Si*×λ*是过阿贝尔的.

(2）由(1）及引理2.4可得.

3 纯正性质

正则半群S称为纯正的，如果幂等元集合E(S）构成子半群.特别的，对于完全零单半群S＝M0［G；I，Λ；P］，若S纯正，则任意的，由引理2.1可得两种情形成立：

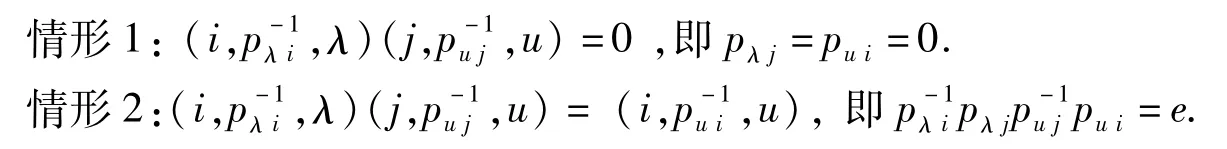
定理3.1令S＝M0［G；I，Λ；P］为一个完全零单半群，且S是纯正半群.对任意的i，j∈I，λ，u∈Λ，若pλi，puj≠ 0，则

证明必要性显然，只需证明充分性.

同样的方法，可以证明其他情形，从而证明了B＝｛e，f，g，h｝为一个子带，且B中不含零.

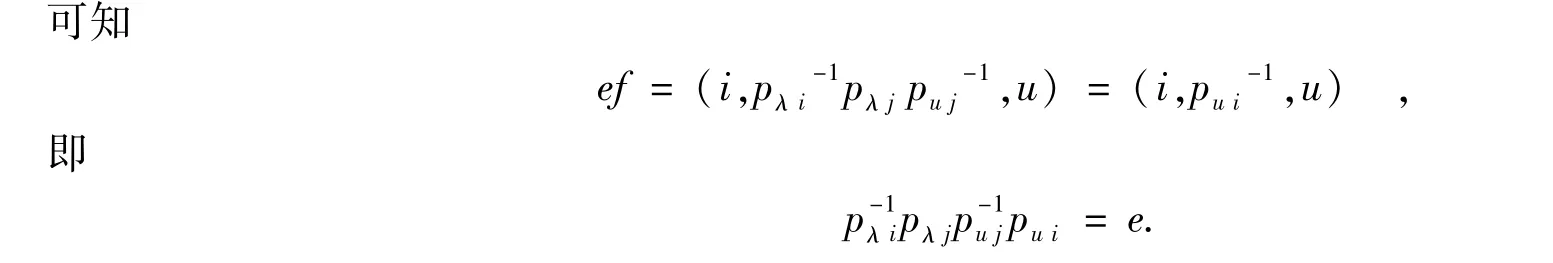
又因为λ＝u或者i＝j，不妨设λ＝u且i≠j，即e L f.下证对任意的g∈B，有g L e成立.

重复上面过程计算gf，结合λ＝u，可得

由(3.1），(3.2）可知ξ＝λ＝u，即g L e.从而B为左零带.类似的，若λ≠u且i＝j，则B为右零带.定理证毕.

［1］ CLIFFORD A H，PRESTON G B.The algebraic theory of semigoups［M］.Rhode Island：Mathematical Surveys of the A-merican Mathematical Society，No7 Providence，R I，1961.

［2］ PETRICH M，REILLY N.Completely Regular Semigroups［M］.New York：John Wiley＆Sons Inc，1999.

［3］ HOWIE JM.Fundamental of Semigruop Theory［M］.Oxford：Oxford Clarendon Press，1995.

Some properties of com pletely 0-sim ple sem igroups

CUIJufen，ZHANG Jiangang
(College of Mathematics and Sciences，Shanghai Normal University，Shanghai 200234，China）

We consider the properties of completely 0-simple semigroup S when the sandwichmatrix P and G are Abelian，and generalize the corresponding results for completely simple semigroups.The elements of S are characterized if the subband of S is a left zero band or a right zero band.And then we characterize the inverses of idempotents of S.

completely 0-simple semigroup；completely simple semigroup；sandwichmatrix

O 152.7

A

1000-5137(2013）02-0120-05

（责任编辑：冯珍珍）

2013-01-12

国家自然科学基金项目( 11201305，11001046）；上海市教委创新项目(12YZ081）

崔菊芬(1987-），女，上海师范大学数理学院硕士研究生；张建刚(1977-），男，上海师范大学数理学院副教授.