风力机叶片优化设计与三维建模
万全喜,张明辉,吴家龙
(山东科技大学机械电子工程学院,山东青岛 266590)
随着环境恶化和能源缺乏等问题的日益突出,各国都把目光聚集在可再生能源上。风能作为一种无污染的可再生绿色能源,越来越引起人们的关注。其中,风力发电是风能利用的主要形式之一[1]。风力机的核心部分是叶片,其主要功能就是将风能转化成机械能,它的转化效率的高低将直接影响并且在很大程度上决定着风力机的性能。因此风力机叶片的优化设计非常重要。传统的Wilson方法是选择同一的最佳攻角α,这样设计出的叶片外形并不是最优,气动性能也有所降低。作者根据叶片的最佳设计攻角α、升力因数CL沿叶片展长方向呈非线性分布,对传统的Wilson方法进行改进,利用MATLAB软件计算叶片外形各参数,优化并修正了200 kW风力机叶片的气动外形。
1 风力机叶片气动外形设计
风力机的叶片气动外形设计非常重要,设计气动性能良好的叶片是风力机获得最大风能利用系数及优良经济效益的关键。风力机叶片的优化设计主要包括对叶片数B、叶片直径D、翼型、安装角θ和弦长C等参数的确定。
1.1 风轮直径D的确定
风力发电机风轮直径,由下面公式确定:
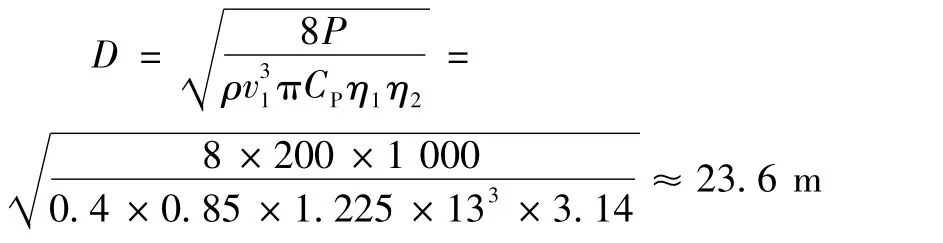
式中:P=200 kW,空气密度ρ=1.225 kg/m3,设计风速v1=13 m/s,风能利用系数CP=0.4,叶片数B=3,风力机的机电效率 η=η1η2=0.85(η1为传动效率,η2为发电机效率)。风轮的直径D为23.6 m,除去中心毂直径后,风轮的半径取R=11.5 m。
1.2 翼型的确定
翼型的选择对风力机的风能利用效率十分重要。一种性能良好的翼型应该是在某一攻角范围内所对应的升力系数CL较高、阻力系数Cd较小;同时所选雷诺数应与风力机实际运行情况的雷诺数接近;此外,还应具有良好的制造加工工艺性。设计风力机时,应该根据不同的设计需要选择不同的翼型。此次设计选择NACA2412翼型。利用Profili软件可以得出NACA2412翼型在不同雷诺数下升阻比随攻角变化的曲线图,如图1所示。
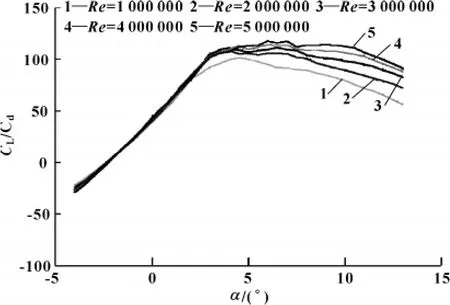
图1 不同雷诺数下升阻比随攻角变化的曲线图
1.3 Wilson优化设计方法的数学模型
传统的Wilson方法是选择同一的最佳攻角α,继而得到安装角θ=φ-α,这样设计出的叶片外形并不是最优,气动性能也有所降低。此次设计是根据叶片的最佳设计攻角α、升力因数CL沿叶片展长方向呈非线性分布,对传统的Wilson方法进行改进。这里在考虑叶尖和轮毂的损失系数的同时 (阻力对气动外形设计影响不大,在此不加考虑),还研究了风轮在非设计状态下的气动性能[2]。从而推导出气动外形设计的基本数学模型:

式中:CP为风能利用系数;a为轴向诱导因子;b为周向诱导因子;Ftip为叶尖修正系数;Fhub为叶根修正系数;F为普朗特修正系数;λ0为叶尖速比;B为叶片数目;φ为叶素入流角 (°);θ为叶素安装角(°);α为叶素攻角 (°);v1为来流风速 (m/s);ν为运动黏度;R为叶轮半径 (m);r为叶素剖面到风轮中心的距离 (m);C为叶素弦长 (m);CL为叶素升力系数。
1.4 Wilson 优化设计步骤[3]
(1)根据叶素理论,把叶片沿展长方向平均分成23等份,得到23个叶素;
(2)针对每个叶素,求解以式 (1)为目标函数、以式 (2)— (5)为约束条件的最优问题,得到每一叶素的a、b、F,进而计算出式 (6)及S;
(3)根据式 (7)和翼型的性能实验数据得到各叶素截面雷诺数Re所对应的最佳攻角α及升力系数CL,进而根据式 (8)求得安装角θ,根据式 (9)求得弦长C;
(4)对求得的叶片弦长C和安装角θ进行拟合修正,使其满足结构、加工工艺等方面的要求;
(5)利用Profili软件可得到翼型坐标原始数据(x0,y0),最后转变成三维空间坐标 (x,y,z)。
2 叶片优化设计的MATLAB编程
2.1 程序流程
程序流程框图如图2所示。
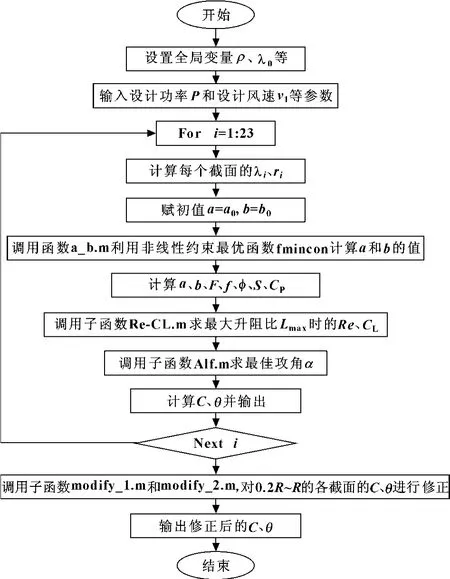
图2 程序流程框图
2.2 利用MATLAB编程解决的关键问题
2.2.1 用MATLAB优化工具箱求解干涉因子a、b
用MATLAB优化工具箱中求解最优化问题最为出色的fmincon函数来求解干涉因子a、b。主程序编写为turbine.m文件,另外创建两个m文件用来存放目标函数和条件函数,分别命名为objfun.m和confun.m。


通过查相关文献,找到以下经验性初值公式[4]:

式中:λ0为叶尖速比;R为风轮半径 (m);r为某一截面叶根的距离 (m)。
2.2.2 求解雷诺数Re及升力系数CL
通过Profili软件,可以求得任何雷诺数Re在各攻角下所对应升力系数CL和阻力系数Cd,及其所对应的升阻比L=CL/Cd。升阻比是叶片设计的一个重要性能指标,为了得到最大风能利用系数,就要使升阻比趋于最大值。利用MATLAB优化工具箱中的max函数求解各给定雷诺数Re_s下接近最大升阻比Lmax所对应的升力系数CL_g和攻角α_g。利用MATLAB优化工具箱中拟合函数polyfit(Re_s,CL_g,4)拟合雷诺数与升力系数,拟合多项式如下:

根据公式 (7)和 (9)推算出:
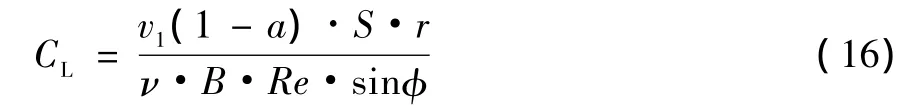
将公式 (15)和 (16)联立,利用MATLAB优化工具箱中的非线性方程组求解函数fsolve求解方程组,得到各截面最大升阻比Lmax下所对应的Re和CL。
2.2.3 求解最佳攻角α
利用上述方法计算求得的Re,利用MATLAB中线性插值函数 interp1(Re_s,α_g,Re,’*spline’)[5],解得最佳攻角 α。
2.2.4 叶片弦长C和安装角θ的修正
经过主程序计算获得了理想叶片弦长C和叶片安装角θ。可是,此时叶片的弦长C和安装角θ是沿叶片展长方向呈非线性分布的,并且叶片根部弦长太大。这种形状的叶片加工困难,用料也不经济。为解决此问题,需要同时考虑叶片气动性能及制造两因素对理想的叶片弦长C和安装角θ进行修正。叶片从风中获得功率的75%是由叶片的前半部分汲取的,叶片根部主要起连接和支撑作用,对风能利用系数CP影响较小。因此选取0.5R~0.9R的各截面,利用MATLAB 工具箱中拟合函数 polyfit(r,C,4)[5]对叶片根部弦长修正,使叶片弦长C适当减小。拟合多项式如下:
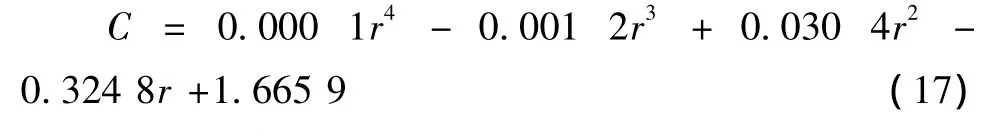
同样利用拟合函数polyfit(r,θ,4)对叶片根部安装角修正,使叶片安装角θ适当减小。拟合多项式如下:
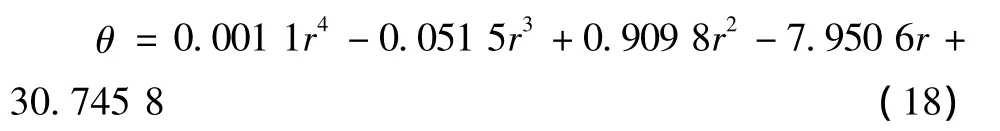
将0.2R~R各截面的r值代入公式 (17)和 (18),得到修正后的弦长C和安装角θ。经过多次实验,采用4次拟合多项式保证了拟合精度,同时也使叶根处弦长C和安装角θ得到减小。
叶片弦长C、安装角θ修正前后对比如图3、图4所示,各参数计算结果如表1所示。
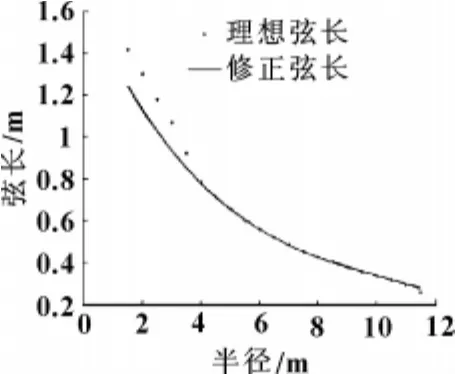
图3 修正前后弦长随半径变化图
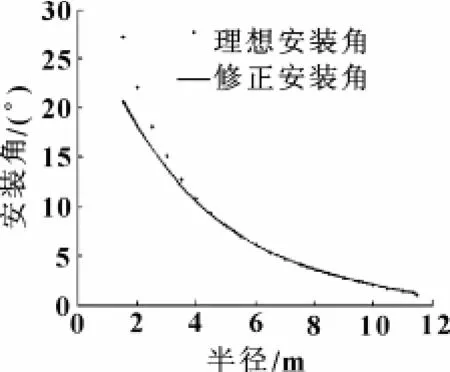
图4 修正前后安装角随半径变化图
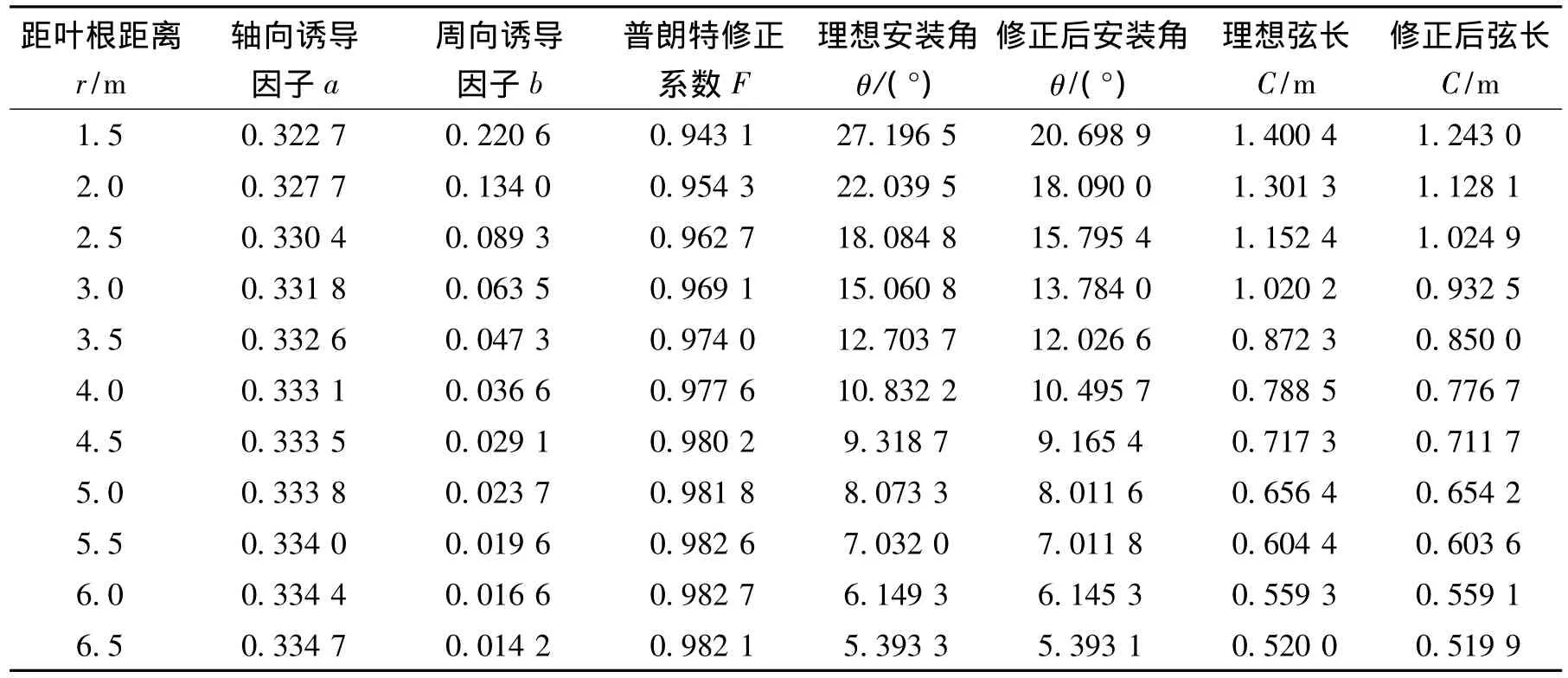
表1 部分叶素截面各参数计算结果数据表
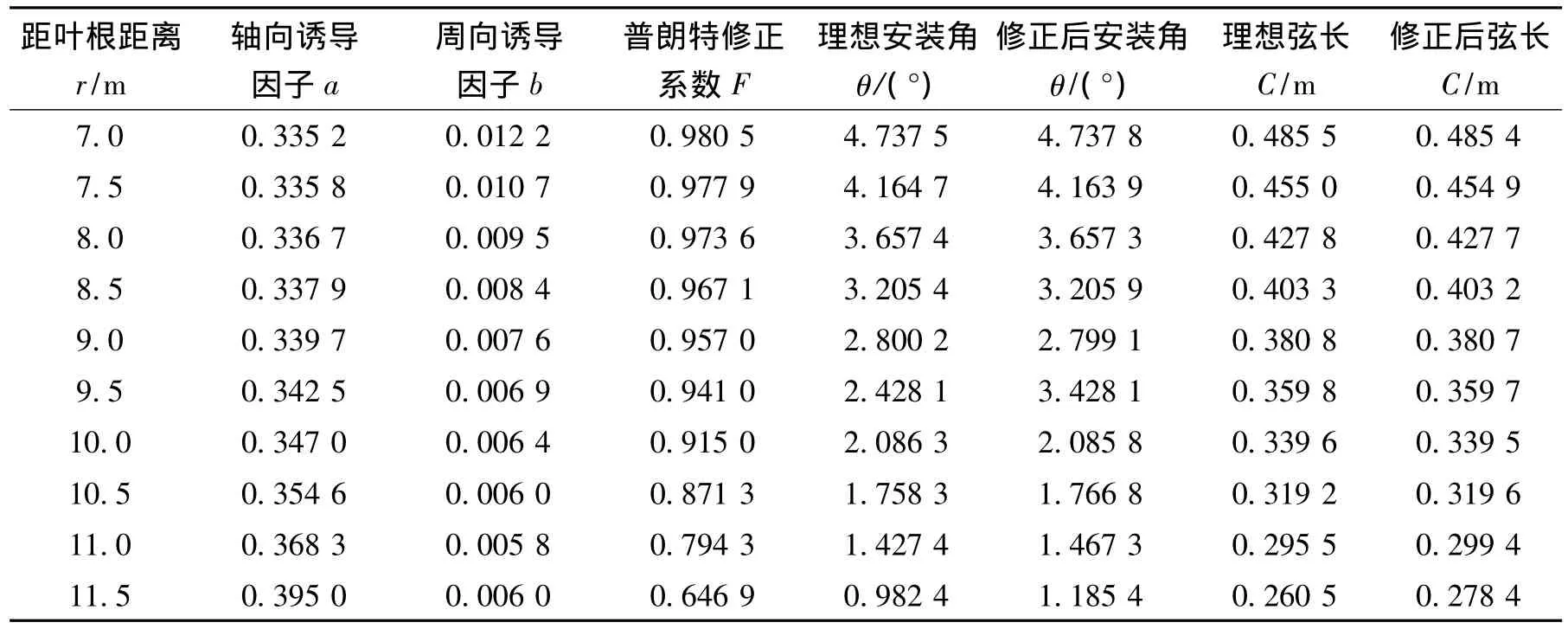
续表1
3 翼型坐标转换[6]
叶片各截面的空间坐标求解实质上就是图形变换,即对组成图形的各坐标点进行变换。基本思路如下:翼型上下弦的原始坐标数据(x0,y0→—) 翼型以气动中心为原点的二维坐标数据(x1,y1→—) 叶素截面各离散点的空间实际坐标 (x,y,z)。原理示意见图5。
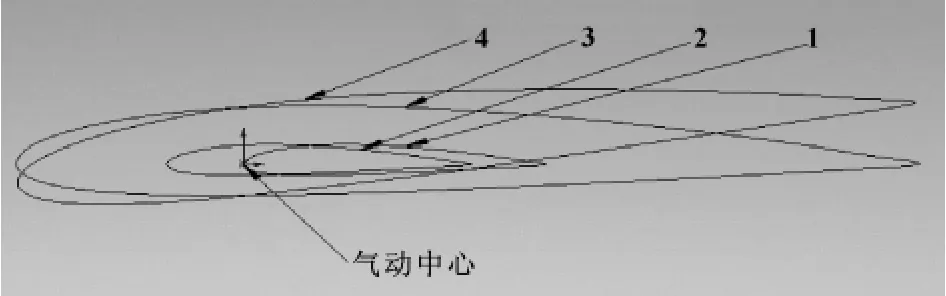
图5 翼型坐标变换示意图
具体步骤如下:
(1)通过 Profili软件获取翼型原始数据 (x0,y0)。
(2)实现翼型1到翼型2的变换。计算以翼型气动中心作为原点、翼弦轴线为x轴的二维坐标(x1,y1)。气动中心通常在到翼型前缘的距离为0.25~0.35弦长处[7],此处气动中心的 x轴坐标设为0.25C,y轴的坐标设为0,设气动中心坐标为 (x2,y2)。
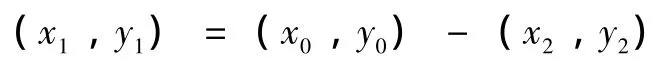
(3)实现翼型2到翼型3的转变。结合弦长计算各叶素坐标:

(4)实现翼型3到翼型4的转变。利用下述公式旋转叶素二维坐标得到三维空间实际坐标 (x,y,z):
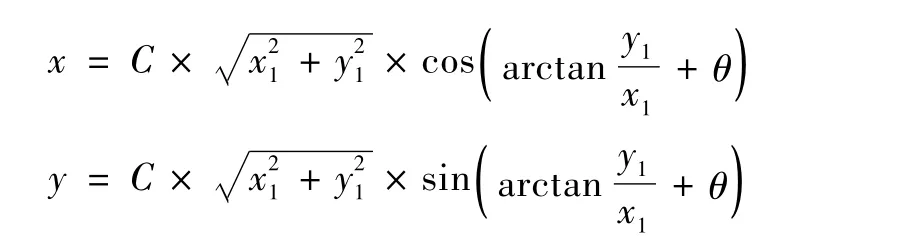
z=r
通过Excel办公软件可完成各叶素上所有离散点空间实际坐标的计算,并把坐标保存为3列数字的txt文件的格式。
4 叶片三维建模[8]
根据上述翼型坐标变换获得的空间实际坐标(x,y,z),通过SolidWorks软件绘制叶片实体模型。具体步骤:利用SolidWorks的“通过xyz曲线”命令绘制各叶素轮廓线 — →利用“平面区域”命令生成叶素平面 — →利用“曲面放样”命令实现在各叶素面间放样生成立体图。
基于表1各参数数据,结合叶柄部分数据,利用SolidWorks软件绘出修正前后叶片实体模型如图6、图7所示。

图6 修正前叶片实体模型

图7 修正后叶片实体模型
5 总结
选用NACA2412翼型,基于MATLAB软件,结合Wilson优化设计方法对叶片各叶素的弦长和安装角进行了求解,考虑到制造性和经济性两方面的因素,又对弦长C和安装角θ进行了修正;然后利用Excel办公软件采用齐次坐标转换的方法对翼型二维坐标进行转换,得到空间三维坐标 (x,y,z);最后应用SolidWorks软件绘出叶片实体模型。此过程简单、通用性强、易于进一步分析,为叶片和其他复杂实体建模提供了新思路。
【1】王晓蓉,王伟胜,戴慧珠.我国风力发电现状和展望[J].中国电力,2004,37(1):81-84.
【2】林闽,张崇巍,张艳红,等.小型风力发电机叶轮设计[J].风机技术,2007(1):28-30.
【3】包飞.风力机叶片几何设计与空气动力学仿真[D].大连:大连理工大学,2008:26.
【4】王凡.风力发电机的叶片设计方法研究[D].南京:南京理工大学,2007.
【5】王沫然.MATLAB6.0与科学计算[M].北京:电子工业出版社,2002.
【6】王学永.风力发电机叶片设计及三维建模[D].北京:华北电力大学,2008:34-36.
【7】贺德馨.风工程与工业空气动力学[M].北京:国防工业出版社,2006.
【8】陈家权,杨新彦.风力机叶片立体图设计[J].机电工程,2006,23(4):37-40.

