高速铁路测量中高斯平面坐标与斜轴墨卡托平面坐标的转换
田林亚,祖力比亚·阿布都热西提,张勇,热比亚·依马尔
(河海大学地球科学与工程学院,南京 210098)
近些年来,中国的高速铁路建设得到了快速的发展。高速铁路作为一种精密工程,对工程测量各个环节都提出了更高的要求。例如,根据《客运专线无砟轨道铁路工程测量技术暂行规定》的技术要求,高速铁路测量的平面坐标系应采用独立坐标系,建立坐标系时应满足投影的长度变形不超过10 mm/km。对于大致呈东西走向的线路来说,如果采用高斯投影方法建立独立坐标系,就需要划分多个投影带进行投影才能满足上述要求,这样就产生了多个独立的坐标系,产生了坐标系不统一和邻带坐标的换算等问题。如果采用斜轴墨卡托投影方法建立坐标系,投影时将圆柱面相切于线路中心线附近,这样既可以保证投影的长度变形值不大于10 mm/km,且可以获得统一的坐标系。本文主要研究高斯平面坐标向斜轴墨卡托平面坐标的转换模型,并结合实际工程数据进行计算与分析。
1 由高斯平面坐标计算斜轴墨卡托平面坐标的模型
墨卡托投影是一种保角圆柱投影,它以圆柱作为投影面,将经纬线先投影到圆柱面上,再将圆柱面展开成平面。圆柱面与地球相切,当切线处于斜位的状态下时便为斜轴墨卡托投影,如图1所示。

图1 斜轴墨卡托投影
采用斜轴墨卡托投影时,如果把地球视为椭球,计算过程将极其繁琐与不便,在几百千米的范围内把地球视为半径相同的圆球是可行的,如果线路太长,则可以采用分段处理的方法。值得注意的是,在大范围内把地球看做圆球来处理所产生的误差将是不容忽略的。
1.1 投影圆球体的选取
斜轴墨卡托投影中,投影圆球的定位应满足:参考圆球体的中心位于国家空间直角坐标系的Z轴上;定向应满足参考圆球体三维坐标系的Z轴与国家空间直角坐标系的Z轴重合,X轴和Y轴分别与国家空间直角坐标系的X轴和Y轴平行。
设线路中某个已知点在国家坐标系中的高斯平面坐标为(B,L),由高斯投影反算公式(1)可计算该点在国家坐标系中的大地坐标(B,L)。
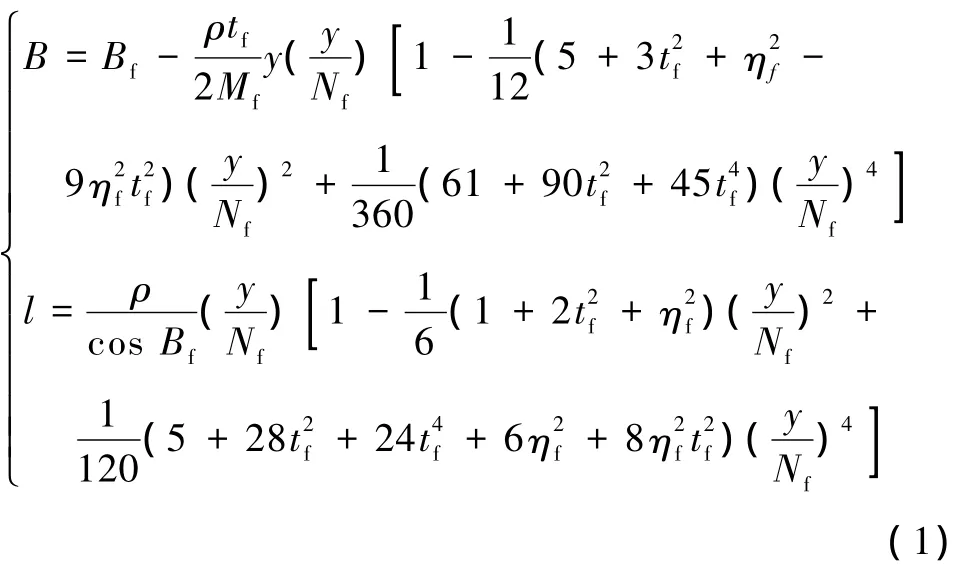
式中,l为经差,Bf为垂足纬度,ηf、tf分别为按 Bf值计算的相应量。
再根据式(2),由该点的国家大地坐标(B,L,H)计算其空间直角坐标(X,Y,Z)。
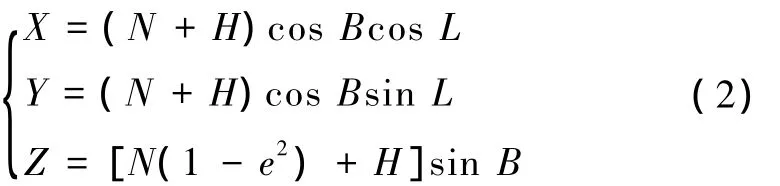
现假设参考圆球体中心O'位于国家参考椭球中心O下方,如图2所示,O'O的长度为S,那么线路上该点在以O'为原点的空间直角坐标系中的坐标为(X,Y,Z+S)。定义圆球的半径为 R,R根据式(3)计算得到。

图2 参考圆球体示意

根据式(3)可列出如下误差方程式

式中,S0和 R0分别为 S和 R的初始值,R0
当线路中有2个以上已知点时,可通过最小二乘法求得dS和dR,从而计算出S和R。
1.2 计算任意一点相对于参考圆球体的大地坐标
因为地球参考圆球的定向、定位与地球参考椭球的定向、定位原理是一样的,所以在计算任意一点位于参考圆球体上的大地坐标(φ1,λ1,H1)时,可采用式(6)计算得到。

式中,φ1为纬度,λ1为经度,H1为大地高。
1.3 计算任意一点相对于圆球体和斜轴的大地坐标
如图3所示,假设AB为线路走向上的两点。首先在球面上建立以A点为极点、以AP为极轴的球面坐标系,根据球面三角公式可推得式(7),并可计算出线路上任意一点的极坐标(θ,ρ)。


图3 斜轴投影大地坐标计算示意
其次,确定斜轴圆球。以过AB的大圆弧为中央子午线,则沿线任意一点各点在斜轴圆球上以A为极点、AB 为极轴的极坐标 θ'和 ρ'为

式中,θB为B点的 θ坐标。
最后,计算任意一点在斜轴圆球上的大地坐标。取极点A为工程独立坐标系的原点,则极点A在斜轴圆球上的经纬度为(0,0)。根据球面三角公式可得到由极坐标计算大地坐标的计算公式:

式中,(φ2,λ2)为所求点在斜轴圆球上的经纬度。
1.4 参考圆球体的投影正算
投影正算就是根据投影条件将参考圆球面上的大地坐标(φ2,λ2)换算成投影面上的平面坐标(xm,ym)。基于斜轴圆球体的投影正算与高斯投影正算类似,等角投影的条件是

式中,r为平行圈半径,M为卯酉圈半径。当投影球体为圆球时,其条件式可表达为

参考高斯投影正算公式,由于 xm是经度差λ2的偶函数,ym是λ2的奇函数,可假设

其中,a0、a1、a2、a3…为只包含 φ2的函数,且 φ2、λ2应化为弧度形式,对式(12)求偏导得

将式(12)、式(13)分别代入式(10)中,由于在起点处有λ2=0,则点(0,φ2)投影后的平面坐标为(R·φ2,0),即 xm=a0=R·φ2,因此解得各个系数为

式中,(φ2,λ2)为所求点在斜轴圆球上的经纬度,R为圆球半径。将上述系数代入式(11),便可求得任意一点的斜轴墨卡托平面坐标(xm,ym)。
2 实例计算与分析
如图4所示,设某条高速铁路线路长400 km,宽15 km,大致呈东西走向,首级平面控制网中的6个控制点采用GPS测量,并将测量成果转换为北京54坐标系中的平面坐标,为了控制投影的长度变形值不大于10 mm/km,分成6个高斯投影带进行投影,其高斯平面坐标及投影变形见表1。

图4 线路及控制点略图

表1 高斯平面坐标及投影变形
从表1数据可以看出,将线路首级平面控制网分成6个投影带进行投影和平差计算,每个控制点到相应投影带中央子午线的投影长度变形都小于10 mm/km,满足了有关高速铁路测量规范的要求,但是分成6个投影带分别进行投影计算,就形成了6个独立平面坐标系,产生了坐标系不统一的问题,在相邻点的综合使用过程中,不仅需要频繁的换带计算,还可能存在较大的投影变形。
如果采用斜轴墨卡托投影方法来建立平面坐标系,并且取点 ZX1为起点,取点 ZX6为终点,取点ZX1和点ZX6所在圆弧为斜轴墨卡托的投影中线,根据本文探讨的坐标转换方法和流程,采用C号.NET编写相应的坐标转换计算程序,将表1中的高斯平面坐标换算成斜轴墨卡托平面坐标,结果见表2。

表2 斜轴墨卡托平面坐标及投影变形
从表2的数据可以看出,斜轴墨卡托投影产生的长度变形远小于高斯投影产生的长度变形。ZX5距离投影中线的距离为12 km,投影变形最大,但是远小于10 mm/km。采用斜轴墨卡托投影,这6个控制点同属一个坐标系,坐标系也得到了统一。
另外,对斜轴墨卡托投影进行有关计算表明:当线路长度为几百千米时,为了使所有的投影变形小于10 mm/km,线路至投影中线的最大横向距离应小于25 km;如果线路长度达到几千千米或者最大横向距离超过25 km,应该将线路分成几段进行投影,且相邻投影带之间应有适当的重叠区域。
3 结论
对于呈东西走向的高速铁路,在建立平面坐标系时应特别注意投影的长度变形问题。当线路较长时,为了控制长度投影变形,可以采用高斯分带投影,但也因此产生了坐标系不统一问题,如果分带过多,在控制点坐标的使用中也带来了坐标换带计算的麻烦。采用斜轴墨卡托投影,可有效地解决高斯分带投影导致的一些问题。
本文对高斯平面坐标向斜轴墨卡托平面坐标的转换模型进行了研究,详细地阐述了坐标转换的方法及其流程。对某条长约400 km的高速铁路测量数据,先采用高斯分带投影的方法进行控制点坐标及投影变形的计算,认为分6个带投影可以满足投影变形不大于10 mm/km的要求,但同时也产生了6个独立坐标系。采用斜轴墨卡托投影和本文研究的坐标转换方法,不仅显著地减小了投影变形,也将6个高斯带中的坐标转换到1个斜轴墨卡托投影带中,使6个控制点的坐标系统得到了统一。计算、分析和实际应用表明,本文研究的方法是正确的。
[1]卢建康,刘华.高速铁路精密工程测量技术体系的建立及特点[J].铁道标准设计,2010(S1):70-73.
[2]李全海.斜圆柱投影及其对 GPS空间坐标的转换模型[J].同济大学学报,2002(1):106-110.
[3]陆鹏程,林冬伟.斜轴墨卡托投影模型及其应用分析[J].铁道勘察,2010(4):26-29.
[4]吕慧玲.斜轴墨卡托投影方法在郑西客专中的应用研究[J].测绘信息与工程,2009(34):26-28.
[5]陈光金.铁路精测网对桥隧施工测量的影响分析[J].铁道标准设计,2010(S1):82-84,117.
[6]王卫红,刘云东.武广客运专线满足无砟轨道控制测量的方案探讨[J].铁道标准设计,2006(S1):197-200.
[7]李晓娥.任意带高斯正形投影平面直角坐标系统在武广客运专线勘测设计中的应用[J].铁道标准设计,2006(S1):195-196.
[8]郭纪明,孔元祥.控制测量学(上下册)[M].武汉:武汉大学出版社,2007.
[9]张正禄,等.工程测量学[M].武汉:武汉大学出版社,2005.
[10]王解先,伍吉仓,高小兵.斜轴墨卡托投影及其在高铁建设工程中的应用[J].工程勘察,2011(8):69-72.
[11]李付伟,刘灵杰,王晓智.斜轴墨卡托投影的长度变形分析[J].河南科技,2012(2):80-81.
[12]刘家臣.高速铁路精密工程控制测量精度研究[J].测绘与空间地理信息,2011(12):216-218.

