既有大型客运站最高聚集人数仿真计算
靳添舟
(哈尔滨地铁集团有限公司运营分公司,哈尔滨 150086)
根据《铁路旅客车站建筑设计规范》(GB50226—95)关于旅客最高聚集人数的定义为:最高聚集人数为车站全年上车旅客最多月份中一昼夜在候车室内瞬时(8~10 min)出现的最大候车人数(含送站)的平均值。也就是一个车站运送旅客多月份中每日瞬时所出现的最多旅客数量的平均值。这一定义是20世纪50年代计划经济时期确定的,当时的新线建设多,客运规模基本上按计划控制[1]。但它又是铁路客运站设计的重要指标[2]。传统计算铁路客运站最高聚集人数的方法有着简单、参数较少、便于操作的优点。但是,它们也存在一些不足,难以满足高速铁路及客运专线车站的设计。计算旅客最高聚集人数必须考虑到以下几点:(1)明确旅客在车站内停留的时间长短,做出最准确的估计和预测;(2)明确列车的发车间隔;(3)避免用到一些经验数据和参数,遵循科学的数据调查依据建立计算模型。鉴于以上分析,运用先进的计算机计算技术并通过Simio仿真建模将可以实现上述要求。
1 铁路客运站最高聚集人数仿真建模
1.1 数量建模
文献[3]根据对北京站、北京西站、广州东站、合肥站和无锡站的大量调查,发现旅客到达车站提前时间的分布近似服从对数正态分布
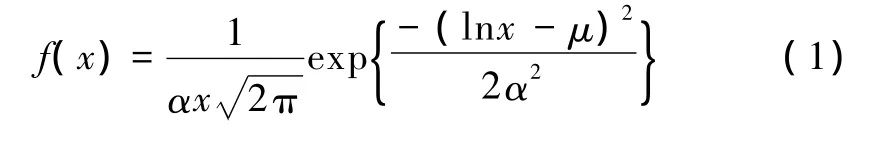
式中 f(x)——旅客到达概率分布函数;
x——旅客提前到达时间;
μ、α——待估参数,分别表示均值和方差。
文献[4]认为在公交化运营的情况下,旅客出行时间较少考虑列车的出发时间,而以自己的出行时间为主,此时,旅客的到达事件基本符合泊松事件流,可以表示为
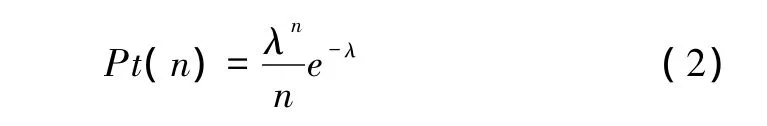
式中 Pt(n)——在单位时间内到达 k个旅客的概率;
λ——到达流的强度,可以根据实际客流量进行取值。
考虑到Simio输入流的产生需要旅客到达间隔时间的约束,旅客进入仿真区域是个随机性事件,本文依据调查比例,得到在每5 min每次列车到达的旅客人数。其数学模型如下

式中 Ci——第 i时段旅客到达人数;
λi——第i时段旅客到达概率;
C——本次列车旅客发送人数;
i——时段(单位 5 min)。
旅客如果想要进入车站,首先需要面对的是选择进站口。由于车站可能有多个入口,可通过统计的方法以概率的形式将客流分配到各个入口。当旅客进入车站候车室后,首先需要通过安全检查机的扫描。为了将通过安检的速度控制在最接近实际情况的水平,将通过安全检查机的时间分布定义为三角分布,如下
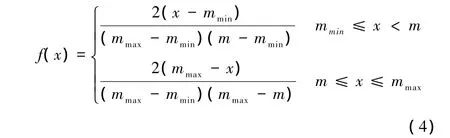
式中 m——旅客可能通过安检的时间;
mmin——旅客通过安检时间最小值;
mmax——旅客通过安检时间的最大值。
旅客进入候车室后,控制旅客离开的时间就是旅客进入检票口上车的时间,为乘坐该次列车发车前的20 min。根据列车时刻表即可完成旅客在候车室内停留时间的控制。同旅客通过安全检查机一样,旅客通过检票口的速度也是一个快速且容易控制的过程。运用三角分布定义其最大值和最小值即可完成对于旅客通过检票口的时间控制。
1.2 基于Simio的逻辑建模
根据Simio面向对象的仿真机制,联系旅客在候车室内的候车行为,分别运用 Simio当中的 Souce、Sever、Sink模块进行控制,Souce和Sink分别控制旅客进入和离开,3个Sever分别为安全检查站、旅客候车区和检票口。总体逻辑模型如图1所示。

图1 总体逻辑模型
在PassengersArrive系列模块中,通过对RateTable到达率表的输入,可以将旅客提前到达车站的时间以及每5 min内到达的人数进行定义。每一个模块产生一个车次的旅客,这样既便于定义每列车的人数,也可以根据每列车的发车时间定义旅客提前到达车站的实际时间。如图2所示。
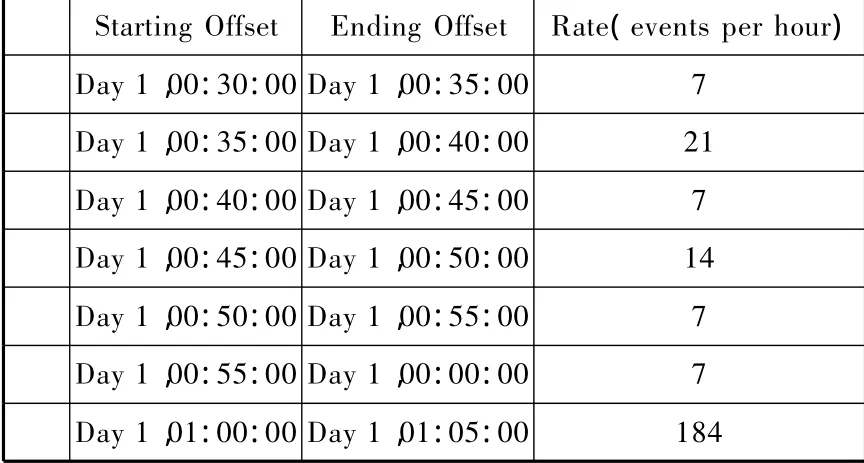
图2 部分到达率示意
仿真时间运行到某一列车发车前20 min时,该车次的旅客将会依次进入检票口检票上车。可以通过对候车区内Timer控制该次旅客离开候车室的具体时刻。如图3所示。

图3 开始检票处理
进入候车区的旅客将被计算到旅客聚集人数中,随着各次列车旅客进入检票口离开,旅客聚集人数也相应陆续减少。通过对旅客聚集人数的监控可以得到在仿真时间范围内的旅客瞬时最高聚集人数,如图4所示。

图4 最高聚集人数计算处理
2 算例分析
2.1 参数及变量定义
本文根据在网上发起的调查,得到了每5 min内旅客提前到达车站的人数的概率。并且根据大连站春运期间统计的1个月内各车次旅客发送人数的均值得到旅客提前到达时刻分布。通过输入RateTable即可实现各车次每5 min内的旅客提前到达车站人数。
根据旅客通过安全检查的实际平均水平,对旅客通过安全检查与检票口的函数进行赋值,如表1所示。

表1 安检参数定义
根据大连站时间运营情况,对发车较密集的10 h进行仿真模拟实验,根据旅客提前到达时刻分布,将仿真时间延长2 h。既总体仿真时间为00∶00~12∶00。根据大连站列车时刻表,按照仿真的时间段,将时间数据进行整合,并定义旅客离开候车室的时间为发车前20 min。
2.2 仿真结果与分析
通过Simio建模仿真计算旅客在候车室的聚集过程,最高聚集旅客人数平均3 160人,半长140人,最小2 810人,最大3 380人。得到旅客聚集高峰时刻为11:55~12:00与15:55~16:00。共产生实体数平均 20 900,半长为 350,置信区间[20 550,21 250],实际输入实体数20 163。故仿真结果具有准确性与可靠性。如表2、图5所示。

表2 仿真结果

图5 旅客聚集人数示意
根据本文前面的介绍,分别运用新型计算方法最坏情景法和既有计算方法聚集系数法对大连站最高聚集人数进行检验计算,根据文献[6-12],送站人员的比例为占到发送人数的15%。故在本文算例中将使用0.15作为送站人员的比例与该次列车的发送人数相乘既可得到该次列车旅客的送站人员人数。具体数值与其他算法得到的数值如表3所示。

表3 计算结果对比
3 结论
针对既有大型铁路客运站客流集散特点,提出了大型铁路客运站候车过程基本仿真流程和仿真模型,建立了基于个体活动的旅客集散仿真模型计算旅客最高聚集人数。通过对大连站春运期间客流的模拟再现,得到大连站旅客最高聚集人数,并且通过既有算法聚集系数法和新衍生出来的算法最坏情景法的检验。结果表明:(1)本文算法可以弥补聚集系数法当中对于密集发车时刻定义的不足;(2)可以防止最坏情景法当中对于旅客聚集情况的过度估计;(3)通过仿真旅客在候车室内的聚集过程,在铁路客运站设计期间即可得到旅客最高聚集人数数值,对于车站的设计和建设起到积极的作用。
[1]郑立勇.铁路客运站最高聚集人数探讨[J].上海铁道科技,2001(1):24-25.
[2]王雪晴.铁路旅客车站站前广场面积指标专题研究[J].铁道标准设计,2007(5):99-102.
[3]何宇强,毛保华,丁勇,张好智,杨静.铁路客运站最高聚集人数模拟计算研究[J].系统仿真学报,2006(1):213-216.
[4]李得伟,韩宝明.铁路客运专线车站乘客集散微观仿真模型[J].交通运输工程学报,2009(2):83-86.
[5]李得伟,韩宝明,李海鹰.大型铁路客运站旅客集散微观仿真[J].中国铁道科学,2009(5):120-123.
[6]邵毓宾.现代铁路旅客车站规划设计[M].北京:中国铁道出版社,1999.
[7]金一兵.模糊数学在预测最高聚集人数中的应用[J].铁道运输经济2003(7):68-70.
[8]王甦男.旅客运输[M].2版.北京:中国铁道出版社,2003.
[9]张天伟.最高聚集人数的定义及方法讨论[J].上海铁道科技,2005(3):13-14.
[10]中华人民共和国铁道部.GB50226—95 铁路旅客车站建筑设计规范[S].北京:中国计划出版社,1996.
[11]杨振海.应用数理统计[M].北京:北京工业大学出版社,2005(3):15-16.
[12]王华.铁路客流高峰期旅客运输特点及对策[J].铁道运输与经济,2004(10):38-39.

