CTCS-3系统中GSM-R网络结构的研究分析
李 冰,朱雅楠
(兰州交通大学自动化与电气工程学院,兰州 730070)
GSM-R通信网络主要是完成我国铁路工作系统中各种数据的传输,实现车载与地面的双向通信[1]。若GSM-R出现故障,这些信息的传输将会中断。为了尽可能地减少通信失败的概率,防止事故的发生,CTCS-3对其信息传输的可靠性和有效性有很高的需求。
目前,已有许多关于可靠性与有效性通信系统模型的研究。文献[2]中描述了一个基于 Petri网的ETCS中GSM-R网络通道的有效性传输模型,并列出了一些可能造成无线通信失败的因素。文献[3]提出了一个关于CBTC数据通信子系统的有效性可靠性模型。然而,这些研究均不是针对 CTCS-3中的 GSM-R网络。通过对文献[2-3]的研究分析,并根据高速铁路信息传输对可靠性与有效性的要求,提出了一个新的GSM-R网络传输结构。
1 CTCS-3的GSM-R网络结构
目前,我国高速铁路上所采用的均为交织双网的网络架构[4],如图1所示。采用交错的基站冗余覆盖方式可以防止无线通信系统内由于单个无线基站的故障而影响整个网络的通信,相对于单网结构来说,它具有更高的可靠性。
文献[1]列出了 GSM-R网络在无线通信时可能出现的一些问题:(1)传输错误,这个问题不时会发生,但我们并不需要采取任何措施,因为在很短的时间内无线网络的连接会自动恢复。(2)越区切换,当列车经过2个相邻基站的重叠区域时,通信会有短暂的中断。列车会终止与当前BTS的通信转而通过切换装置实现与下一个BTS的通信。在高速铁路上,越区切换很频繁,在这之间传输的数据会有很多的错误产生。(3)通信连接的丢失,这可能在越区切换失败或者无线连接超时时发生。

图1 交织双网结构示意
在不同的网络结构和不同的列车速度下,GSM-R无线通信时的这些不稳定因素都将会对整个系统产生不同的影响[5]。现有的GSM-R网络结构采用的是双网交织结构,在列车头部安装2个无线通信终端,其中一个正常工作,而另一个作为其冗余结构备用。基于现有的网络结构,本文提出了一个新的双网交织网络结构:2个无线终端,1个位于列车头部,1个位于列车尾部;每一个终端均在其各自的网络中同时工作。列车头部的终端设备与网络A连接,而尾部的则与网络B连接,形成了2个独立的GSM-R传输通道。在该结构下,可以避免由于越区切换而导致通信中断的发生。当列车头部的无线终端装置位于切换区域(即列车头部位于重叠区域)时,另一个无线终端装置则位于列车的尾部(列车尾部依然位于先前的网络覆盖区域)。该GSM-R的网络结构如图2所示。

图2 新的双网交织网络结构示意
2 可靠性与有效性模型
在该系统中,做如下定义:i∈(0,1,2)表示整个系统的状态,0表示连接失败,1表示与网络A或网络B处于正常通信状态,2表示与网络A和网络B均保持正常通信;j∈(0,1,2)表示系统内传输出现错误的情况,0表示没有错误产生,1表示两个终端设备有1个出现错误,2表示2个终端设备均出现错误;m∈(0,1)表示是否处于切换状态,0表示两终端均未处于切换状态,1表示有1个处于切换状态。在新的网络传输冗余结构下,不可能出现2个无线终端设备均处于切换状态,列车两端的无线终端设备是不可能同时位于切换区域的。n∈(0,1,2)表示系统是否连接正常,0表示连接正常,1表示其中1个没有连接,2表示2个均没有连接。因此,整个系统状态可以由(i,j,m,n)表示。
基于马尔可夫过程,提出了2种GSM-R网络结构的可靠性模型。
2.1 可靠性模型
2.1.1 双网交织网络结构
图3描述了双网交织网络的马尔可夫转化过程。在该模型中,传输出现错误、切换或连接的失败都将会导致系统通信的失败。λ1、λ2、λ3分别表示从正常状态 (1,0,0,0)到失败状态(0,1,0,0)、(0,0,1,0)、(0,0,0,1)之间的概率。
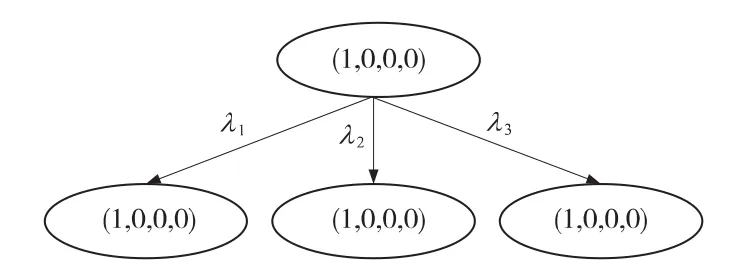
图3 传统交织双网结构马尔可夫状态转化
交织双网结构的可靠性模型可以通过式(1)描述
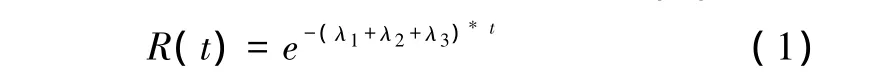
2.1.2 新的网络传输结构
在新的网络结构下,当其中一个无线终端设备出现传输错误、切换或连接失败等时并不会导致整个系统的通信失败。图4描述了新结构下的马尔可夫状态转化过程,λ1、λ2、λ3表示传输错误、切换或连接失败的概率。μ1、μ2、μ3表示这些错误发生后的修正概率。

图4 新网络结构的马尔可夫状态转化
状态(2,0,0,0)定义为 P0,表示 2 个网络(A 和B)均正常,(1,1,0,0)、(1,0,1,0)、(1,0,0,1)分别定义为P1,P2,P3,表示网络A或网络B有一个不正常而整个系统网络是处于正常的状态。状态(0,1,1,0)、(0,2,0,0)、(0,1,0,1)定义为 P4,状态(0,1,1,0)、(0,0,1,1)定义为 P5;(0,1,0,1)、(0,0,1,1)、(0,0,0,2)定义为 P6;当系统处于 P4、P5、P6这 3 种状态时通信失败。
参数定义如下

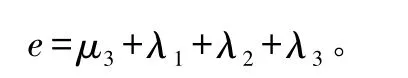
该系统的转移矩阵Q如下所示
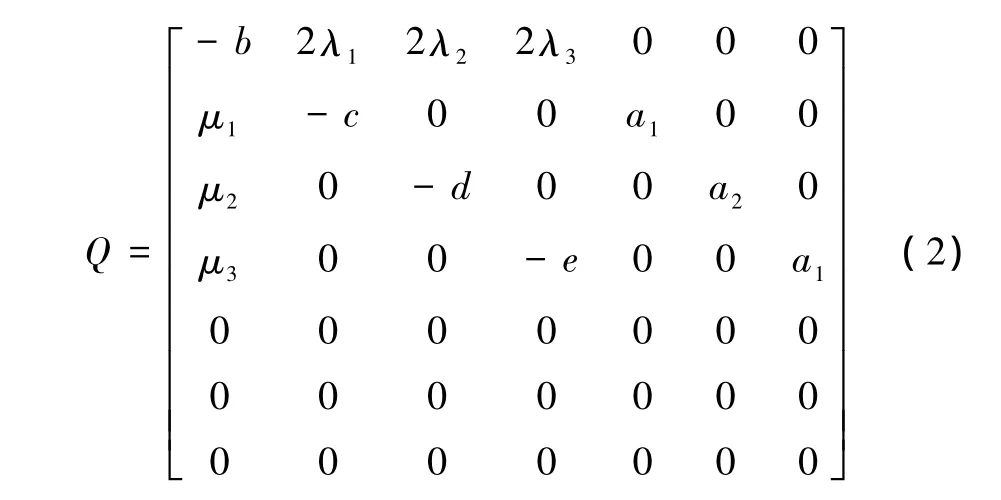
由此算出状态转移概率矩阵

转移概率矩阵表示由正规状态 P0,P1,P2到吸收态 P4,P5,P6之间的转化,如下式所示
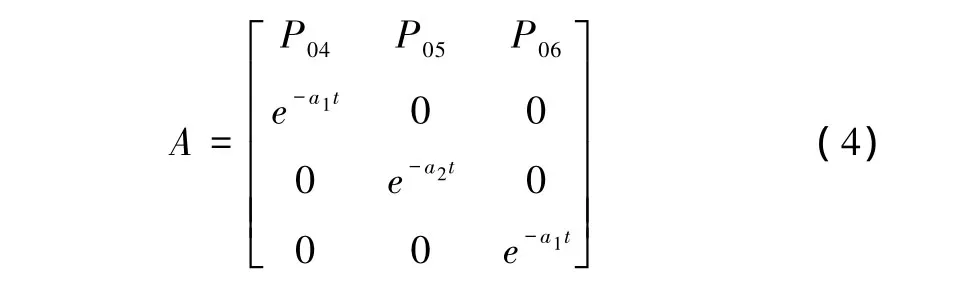
接下来可以算出矩阵A
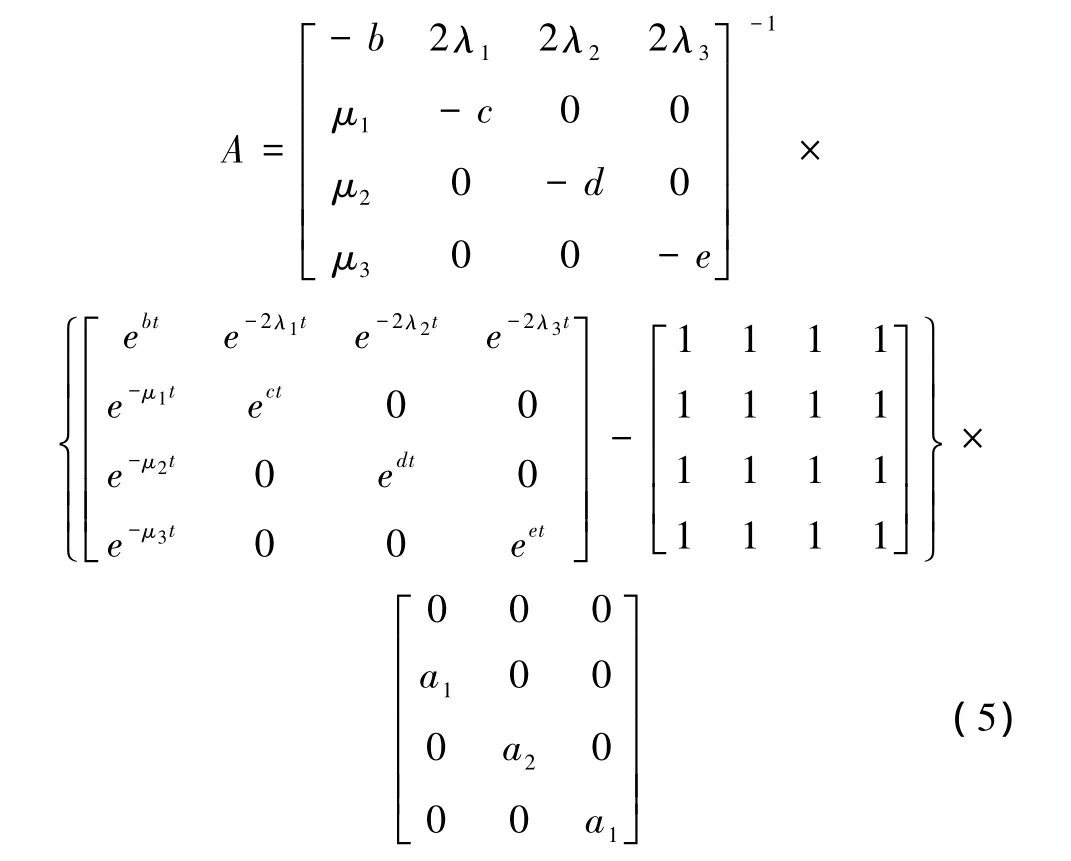
由公式(5),得出从原始状态P0到吸收态 P4,P5,P6的转化概率。并且,由于从P0到P0~P6之间的转化概率之和为1,可以得到该系统的可靠性。
2.2 有效性模型
2.2.1 交织双网覆盖
图5描述了交织双网覆盖的马尔可夫转化过程。与图3不同的是,它考虑了传输错误和切换或连接的失败时的自恢复概率。分别定义 μ1、μ2、μ3表示从失败状态(0,1,0,0)、(0,0,1,0)、(0,0,0,1)到正常状态的转化率。

图5 传统交织双网结构马尔可夫状态转化
依据系统的稳定性,可以通过状态(1,0,0,0)算出系统的有效性,用 π0表示。将状态(0,1,0,0)、(0,0,1,0)、(0,0,0,1)的稳定性分别定义为 π1、π2、π3。可以得到该系统的转移矩阵

P0,P1,P2,P3状态对应的稳态系数矩阵为:π =[π0,π1,π2,π3]T。
基于时间连续的马尔可夫链理论
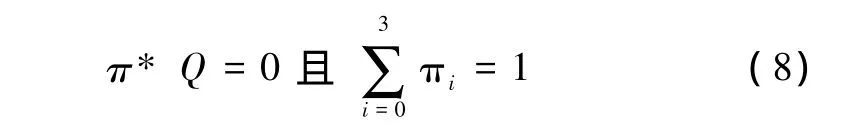
得到
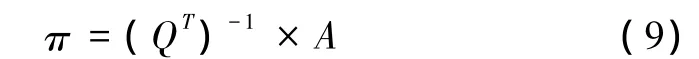
由于各行矩阵彼此之间存在关联,在QT矩阵中,可以用[1,1,1,1]代替一个行矩阵。且 A=[0,0,0,1]T,π0为矩阵π的第一行矩阵,表示状态 P0的稳定概率。
于是,可以得到系统的有效性

2.2.2 新的网络传输结构
图6描述了新网络结构的马尔可夫转换过程。该过程与图4不同,它考虑了系统由失败状态 P4,P5,P6恢复到正常状态P1,P2,P3的概率。该系统的有效性可以通过计算(2,0,0,0)、(1,1,0,0)、(1,0,1,0)、(1,0,0,1)状态的概率得到,分别用 π0、π1、π2、π3来表示;用 π4、π5、π6来表示状态 P4,P5,P6的稳态概率。
假设 f=μ1+μ2+μ3,g=μ1+μ3
则该系统的转移矩阵如下
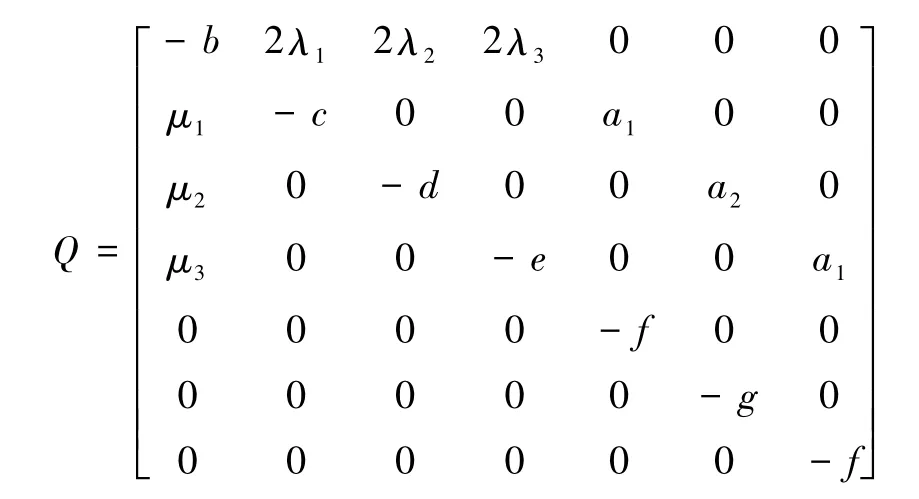
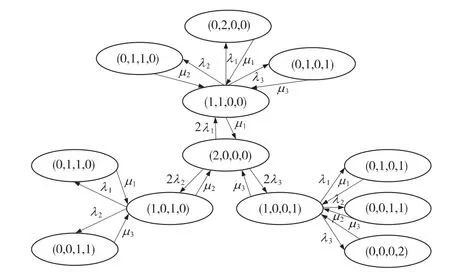
图6 新网络结构的马尔可夫状态转化
由 π=(QT)-1×A,得到 P0~P6的概率矩阵

通过式(14)得到该系统的有效性

3 仿真结果
由于传输错误具有随机性,使得它有一个指数分布的延时,该延时时间不低于由于传输错误产生的通信失败的平均时间[6]。由其指数分布函数

可以算出参数λ1的值
λ1=≈0.007 33,其中 p=0.95,x=7
由于GSM-R网络为线状覆盖,切换发生的频率可以由λ2=v/d得到,其中,v表示列车的速度,d表示BTS的平均距离。CTCS-3中列车的速度可达500 km/h,d的值为 3 km。
根据技术规范要求,尽可能的降低一个完整的连接丢失的概率,最多允许每1万h1次,由此λ3的值为2.78×10-6次 /s[7]。
从文献[2]中可以得到用于MATLAB仿真的参数值为
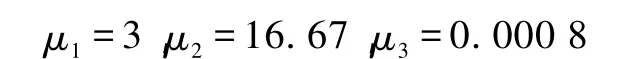
图7比较了2个结构对应的可靠性。新网络结构相对于传统的网络结构来说可靠性更高。考虑到切换是造成整个系统通信失败的主要原因,在新网络结构中,无线终端设备被安装在不同的位置使其不会同时处于切换区域。系统将会始终保持正常状态。
传统的交织双网结构更容易受到列车速度的影响。速度越高,其可靠性越低。然而新的网络结构几乎不受到列车速度的影响。从图7中可以看到,速度不同时,其曲线几乎一致。
图8显示了2种结构在工作状态下的逗留时间。传统的网络结构下,参数 λ2=0.046 2,由此可以算出

图7 2种结构可靠性的比较
图8中的逗留时间曲线。
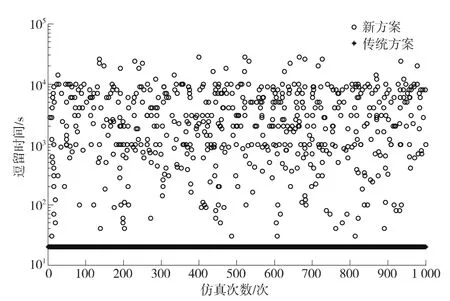
图8 2种结构下逗留时间的比较
新的网络结构下,有 P0,P1,P2,P3四种状态。P1,P2,P3的恢复率是不一样的。图9显示了该冗余结构逗留时间的分布情况。通过对系统进行的1 000次仿真结果的分析可以得到:新的结构在工作状态上的逗留时间较传统结构下的逗留时间要长。

图9 新方案逗留时间分布的仿真
影响系统可靠性的主要因素是越区切换,其切换率是由列车速度和BTS之间的平均距离决定的。图10显示了系统的有效性随列车速度增大时的变化曲线。从图中可以看出。新网络结构的有效性始终高于99.99%,而传统的结构下有效性最大为99.4%,并且当列车速度到达500 km/h时降为99.3%。因此,新的网络结构的有效性比传统结构的要高且受到列车速度的影响也很小。随着列车速度的增加,切换的频率也越高,新的网络结构可以很好的降低系统受到切换的影响程度。

图10 两种结构的有效性比较
4 结语
GSM-R作为一个通信网络,高可靠性是保证列车安全可靠运行的基础。本文主要针对于现有的GSM-R网络结构,提出了一个新的网络传输结构。利用马尔可夫理论分别对其可靠性、有效性进行了研究分析。通过分析表明:新的网络结构在可靠性和有效性上均优于传统的网络结构,并且其受到列车速度的影响也更小。
[1]M.Uhlirz.Concept of a GSM -based communication system for high-speed trains[J].in Proc. IEEE 44th Vehicular Technol.Conf.,Stockholm,Sweden,1994:1130-1134.
[2]Armin Zimmermann and Gunter Hommel.A Train Control SystemCase Study in Model-Based Real Time System Design[J].Ininternational Parallel and Distributed Processing Symposium, IEEE,2003:118-126.
[3]Tianhua Xu,Shu Li and Tao Tang.Dependability Analysis of Data Communication Subsystem in Train Control System[J].Journal of BEIJINGJIAOTONG-UNIVERSITY,2007,31(5).
[4]铁道部工程设计鉴定中心.中国铁路GSM-R移动通信系统设计指南[M].北京:中国铁道出版社,2008:82-93.
[5]Stephen Dudoyer,Virginie Deniau,Ricardo Adriano.Study of the Susceptibility of the GSM-R CommunicationsFace to the Electromagnetic Interferences of the Rail Environment[J].IEEE Transactions on Electromagnetic Compatibility,2012,54(3).
[6]ERTMS/ETCS-Class 1.GSM-R Interfaces:Class 1 Requirements.Subset-093 V.2.3.0[S].
[7]UIC Project EIRENE System Requirements Specification V.15[S].

