生产线组织模式比较研究*

刘绘珍，张毕西，张湘伟

(郑州航空工业管理学院管理科学与工程学院，郑州 450015)

0 引言

市场对产品的需求趋于多样化、个性化和动态化，产品品种不断增加，需求批量不断缩小，产品生命周期越来越短，响应客户需求的多样化所进行的多品种中小批量生产已成为生产方式的主流。品种变化带来加工工艺及其顺序的变化，为适应这种随机不确定变化的需求，要求作业系统具备高度的柔性。生产线重组机制是应对市场复杂多变需求的一种系统有效运行模式，是一种具有动态适应复杂需求环境能力的柔性作业系统。借助工人多技能要素，可实现快速改变作业系统结构，适应订单任务随机变化而导致加工工艺频繁变化的要求。

Bokhorst和Slomp(2000)构建了整数规划模型，分配多技能工人到不同工作站，从而有效应对工人旷工和需求波动［1］。Askin和Chen(2006)针对部分工人为多技能的连续式生产线，提出了旨在实现产出最大化的动态任务指派方法，以实现动态产能平衡［2］。Sayin等(2007)考虑工人学习因素提出两阶段分配模型:第一个阶段优化技能集合的效用(即工人总效率);第二阶段，在第一阶段优化条件下，在最大总效率的基础上浮动一定范围，以最大化工人技能为目标分配工人［3］。Vidic(2008)在考虑工人异质性和学习遗忘特性的情况下，研究了在动态岗位共享生产系统，和在工人固定岗位的串联生产系统中研究不同的工人分配调度方案［4］。

1 生产线的组织模式

生产线静态组织模式是指根据任务的工艺要求、工序定额工时、预定交货期、任务总劳动量等，设计和构建生产线组织模式［5-8］。

例:某生产部门要完成某产品任务的生产，该任务需经N道工序加工，有M*N名工人，先研究不同情况条件下生产线可能的三种组织模式。

(1)一人一工序、多线平行组织模式

如图1所示，作业系统有多条相同生产线组成，每道工序配备一名工人。并假设:T=计划期有效工作时间;M=作业系统生产线数;N=每一生产线上的工序数。该组织模式下可分如下三种情况计算计划期总产量。

①设工人在各工序之间单件加工时间相等

工人在各工序单件加工时间用s表示;作业系统计划期总产量为，则有:

图1 一人一工序作业系统组织模式

②设工人在各工序之间单件加工时间不等，工序之间不相互协助

工人单件加工时间用tij(i为工序 /工人编号，j为生产线编号)表示;工序之间不相互协助。此时，各生产线产出效率取决于其中效率最低者，即瓶颈工序。

生产线j中瓶颈工序单件工时为:

并行生产线的计划期总产量为Q2T，则有:

③设工人在各工序之间单件加工时间不等，工序之间相互协助

工人单件加工时间用tij(i为工序 /工人编号，j为生产线编号)表示;工序之间不相互协助。此时，可近似看成，各工序效率达到充分平衡。

各工序平均单件工时:

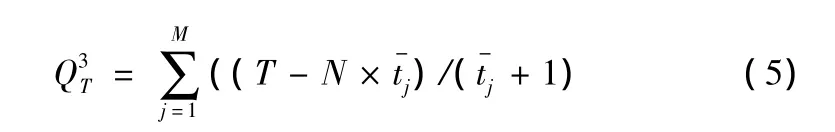
(2)多人一工序，各工序工人数相等

如图2所示，作业系统有多条相同生产线合并组成一条生产线，即每道工序有相同数量的工人组成。并假设:T=计划期有效工作时间;M=每道工序工人数量;N=生产线上的工序数。该组织模式下可分如下三种情况计算计划期总产量。

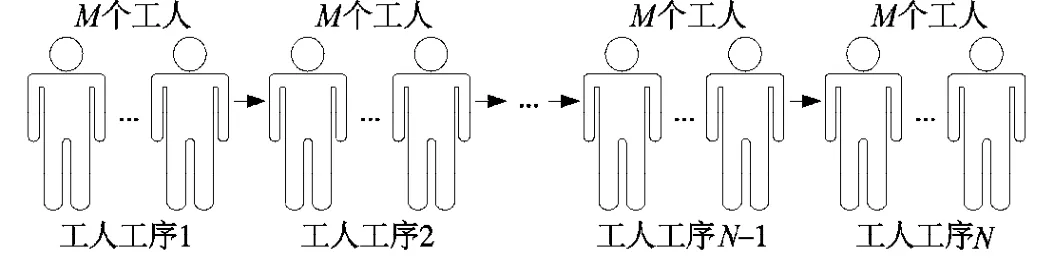
图2 多人一工序组织模式

①设工人在各工序之间单件加工时间相等

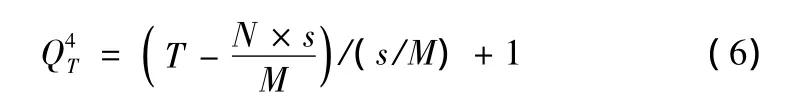
②设工人在各工序之间单件加工时间不等，工序之间不相互协助

工人单件加工时间用tij(i为工序编号，j为工序中工人编号，每道工序中工人独立编号)表示;工序之间不相互协助。此时可用工序平均单件工时、瓶颈工序单件工时表示。

i工序平均单件工时:

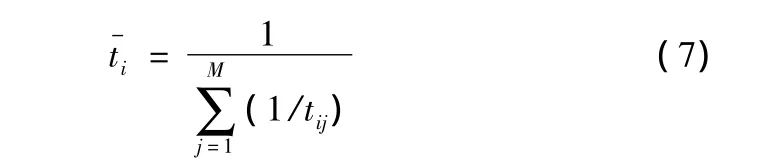
瓶颈工序单件工时:

③设工人在各工序之间单件加工时间不等，允许工序之间相互协助

工人单件加工时间用tij(i为工序编号，j为工序中工人编号，每道工序中工人独立编号)表示;工序之间相互协助。此时，可近似看成，各工序效率达到充分平衡。

各工序平均单件工时:

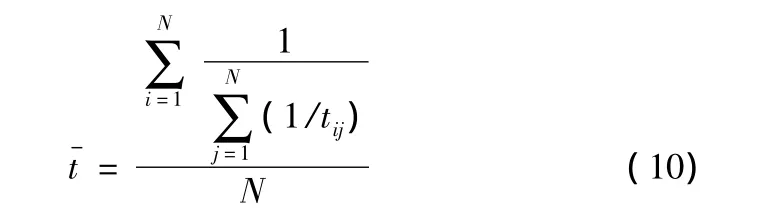
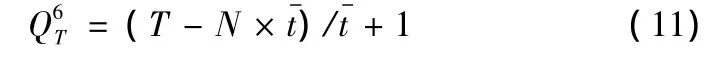
(3)N*M人顺序执行各工序操作

即所有工人同时完成同一工序后，再按工艺流程转到下道工序作业，直至所有工序完工，如图3所示。并假设:T=计划期有效工作时间;M=平均每道工序工人数量;N=生产线上的工序数。该组织模式下可分如下两种情况计算计划期总产量。

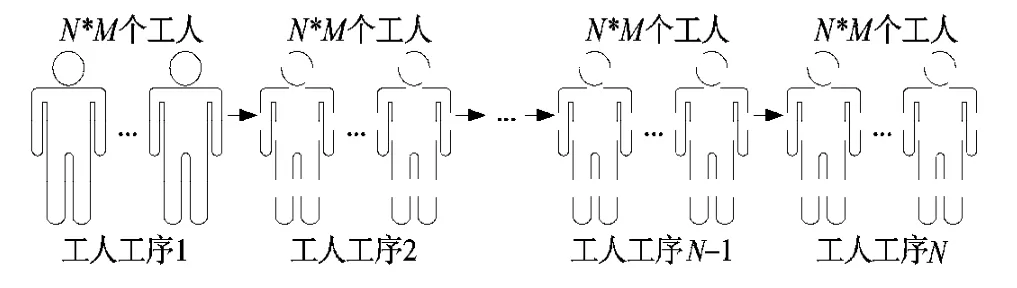
图3 N*M人同时完成相同工序

①设工人在各工序之间单件加工时间相等

工人在工序单件加工时间用s表示;计划期各工序的作业时间为:T/N;各工序出产节拍为:s/(N×M)，计划期总产量为，则有:

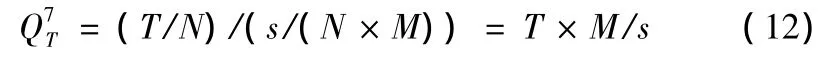
②设工人在各工序之间单件加工时间不等(该组织模式不存在工序协助的问题)

这种组织模式不存在瓶颈工序的影响。工人单件加工时间用tij(i为工序编号，j为工序中工人编号，取值范围从1到N×M)表示。

工序平均单件工时:

2 不同组织模式比较

为了分析上文提出三种组织模式的差异，采用两个算例从数值上进行比较，并做如下假设:

(1)组织模式1中生产线的数量为3，3条生产线中对应工序标准单件加工时间相同;(2)不同工人在相同工序上的生产效率相同;算例1:三条相同生产线上各工序单件标准加工时间均为:［3，2.5，2.4，2.8，2］，单位为分钟。

算例2:三条相同生产线上各工序单件标准加工时间均为:［2.5，2.6，2.7，2.3，2.4］，单位为分钟。

其它参数:T=5000分钟;M=3;N=5。从上面两个算例的参数可以看出，算例1各工序之间标准加工时间差异较大。

2.1 不考虑学习与遗忘情况下的比较

如表1所示，当不考虑工人学习与遗忘时，假设工人的效率均等于各工序单件标准加工时间。为了对上文提到的八种产出进行比较，采用流水线同期化的方法，同期化后各工序单件加工时间相等，将该值赋给 s。即

表1的结果显示:

(1)两个算例均说明组织模式1第二种情况下的产出最小。算例1第二种情况的产出占最大产出的4989/5905=84.49%;算例1第二种情况的产出占最大产出的5544/6000=92.4%。说明各工序单件加工时间差别越大，组织模式1中第二种情况产出越小。

(2)组织模式1和组织模式2中，工序同期化的结果和工序之间相互协助对产出的影响相同。

(3)比较三种组织模式对应情况的产出，模式3大于模式2，模式2大于模式1。且不管各工序单件加工时间差别大小，组织模式3都能得到最大产出，说明该模式具有很好的健壮性。

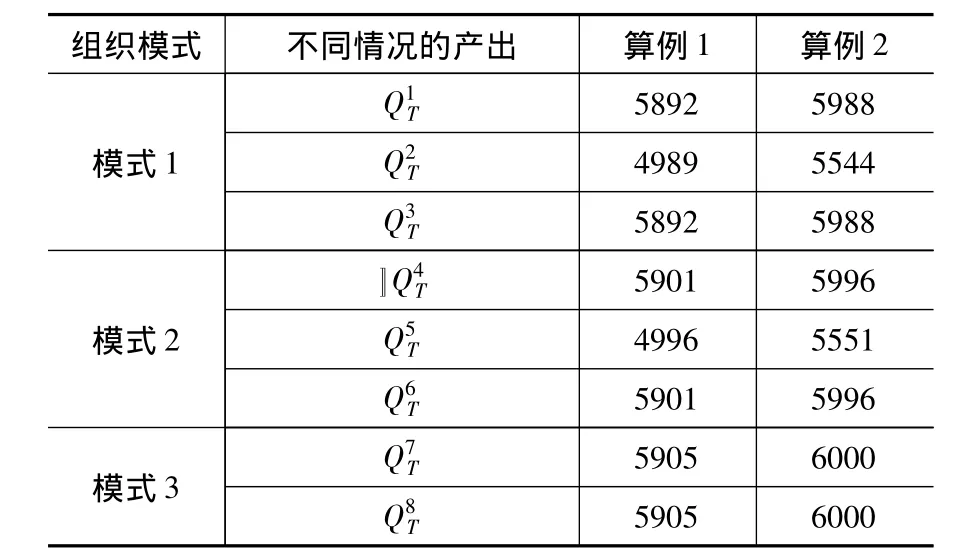
表1 不考虑学习与遗忘的计算结果

2.2 考虑学习与遗忘情况下的比较

实际生产中，工人掌握技能需要一定的培训成本，并且作业的熟练程度受其作业数量的影响，同时也受学习与遗忘的影响。所以，在计算产出时考虑工人的学习与遗忘过程更符合实际情况。本文在研究组织模式对生产系统产出影响的同时考虑工人的学习与遗忘因素，并采用双曲线 －近期学习遗忘模型［9-12］。

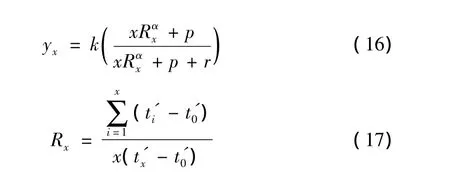
该模型既适用动作学习也适用认知学习，既适用正学习也适应负学习，其包含6个参数，如式(16)所示。

yx表示生产第x个产品时的生产率(单位时间的产出量)，一般情况下，随着加工产品的增多，yx也增大，即生产率增大。

k表示工人达到熟练程度时的生产率，也称为稳态值，即工人能够达到的最大生产率。

r表示工人学习过程中，其熟练程度达到稳态值一半时所需要的生产量。r越大整个学习遗忘曲线越平缓，即学习的速度越慢。

p表示先前的经验，其值越大，初始经验越多，对应初始速度越大。

Rx表示近期习得量。学习的过程中，往往对近期学习的经验记忆深刻，对生产效率的提升所起的作用越大。用式(17)表示，相对应的t'0表示初始做该工作的时间点，t'x表示生产第x个产品的开始时刻，表示生产第x个产品之前所流失的时间。近期习得量Rx表示对近阶段习得量的一个度量，取值0到1之间，趋近0表示学习在很遥远的时间发生，趋近1表示学习在当前最近时间获得。

α表示遗忘率。当工人一段时间不工作或不做该项工作时，就会发生遗忘，α表征遗忘的速度，该值越大遗忘的程度越大。该模型中遗忘表现为在学习量x上打了一个折扣，最终的影响表现为工人加工速度的减少。

根据上文的分析，当工人效率假设在各工序效率相同时，组织模式3的产出最大，但需要每个工人掌握所有技能;组织模式1中的第二种情况产出最小，单技能工人即可满足。从技能学习的角度看，后者学习一项技能，学习速度将更快。

为了揭示不同组织模式中学习与遗忘对产出的影响，选择上面三种组织模式共八种情况产出中的两个极端进行对比研究，即比较组织模式1中第二种情况和组织模式3中的第二种情况。不妨设工人是同质的，即所有工人在各工序作业的熟练程度达到稳态值的一半时所需要的生产量r=500，且所有工人在各工序先前的经验p=r，所有工人在各工序遗忘率 α =1.8。

算例1，当不考虑工人学习遗忘因素时，工人的生产效率总等于加工第一件产品的效率，两种情况下的产出分别为:;考虑工人学习与遗忘因素时，两种情况下的产出分别为:2766=3045。

算例2，当不考虑工人学习与遗忘因素时，工人的生产效率总等于加工第一件产品的效率，两种情况下的产出分别为考虑工人学习与遗忘因素时，两种情况下的产出分别为:Q'2T=3102=3090。

上面两个算例的结果显示:

(1)当考虑工人学习与遗忘因素时，对应产出均增大。算例1两种模式的学习效应分别是(2766－2490)/2490=11.08%，(3045－2952)/2952=3.15%;算例1两种模式的学习效应分别是(3102－2766)/2766=12.15%，(3090－3000)/3000=3%。

3 结论

基于多技能工人和其自组织行为，本文针对生产线的结构和特点分析了生产实践中常用的三种组织模式，以计划期产出量最大为目标，构建了各种组织模式、在不同条件下的计划期产出量模型。采用两个算例进行数值分析，结果显示:若不考虑工人学习与遗忘时，第三种组织模式是最优的;而由于该模式要求工人掌握所有技能，若考虑学习与遗忘时就暴露出该种组织模式的不足，当生产线各工序需求工时差异不大时，模式1得到产出量将大于模式。

［1］Bokhorst，j.and j.slomp.Long-term allocation of operators to machines in manufacturing cells［J］.Group technology/cellular manufacturing world symposium，and Juan，Puerto rico.2000:153 －158.

［2］Askin，R.G.Chen，J.Dynamic task assignment for throughput maximization with worksharing［J］.European Journal of Operational Research，.2006，168:3853.

［3］Serpil Sayin，Selc，uk Karabati.Assigning cross-trained workers to departments:A two-stage optimization model to maximize utility and skill improvement［J］.Production，Manufacturing and Logistics.European Journal of Operational Research.2007，176:1643 －1658.

［4］Natasa S.Vidic.developing methods to solve the workforce assignment problem considering worker heterogeneity and learning and forgetting［D］.The United States of America.University of Pittsburgh.2008.

［5］张毕西，关迎莹，宋静.考虑学习率的人工作业系统批量加工模式优化［J］.系统工程理论与实践，2010(4):622－625.

［6］Suer，G.A.，＆ Tummaluri，R.R.(2008).Multi-period operator assignment considering skills，learning and forgetting in labour-intensive cells［J］.International Journal of Production Research，46(2):469－493.

［7］Chen，J，and Askin，R.G..Throughput maximization in serial production lines with worksharing［J］.International Journal of Production Economics，2006.

［8］Leopairote，K.，Policies for Multi-Skilled Worker Selection，Assignment，and Scheduling［D］.the University of Wisconsin-Madison.2004.

［9］Nembhard，D.A.and M.Uzumeri.Experiential Learning and Forgetting for Manual and Cognitive Tasks［J］，International Journal of Industrial Ergonomics，25，315，2000.

［10］Globerson，S.，N.Levin，and A.Shtub.The Impacts of Breaks on Forgetting when Performing a Repetitive Task［J］，IIE Transactions，1989，21(4):376 －381.

［11］Nembhard，D.A.and M.Uzumeri.An Individual-Based Description of Learning Within an Organization［J］，IEEE Transactions on Engineering Management，2000，47(2):370－378.

［12］Nembhard，D.A.and N.Osothsilp.An Empirical Comparison of Forgetting Models［J］，IEEE Transaction on Engineering Management，2001，48(3):283.