基于Kirchhoff近似法的目标声散射场仿真
熊宏锦, 苑秉成, 詹昊可, 罗银波
基于Kirchhoff近似法的目标声散射场仿真
熊宏锦1, 苑秉成1, 詹昊可1, 罗银波2
(1. 海军工程大学 兵器工程系, 湖北 武汉, 430033; 2. 海军驻九江地区军事代表室, 江西 九江, 332000)
对经典的Kirchhoff公式作一定的假设, 得到收发合置情况下的近似Kirchhoff公式, 进一步对球体目标声散射场进行求解。在MATLAB平台下, 仿真出目标声散射场的相关曲线, 并对声散射场与作用距离和入射波频率的关系进行了对比分析。应用表明, 结论对于水下掩埋目标探测与识别的研究具有一定实用价值。
Kirchhoff近似法; 收发合置; 声散射场
0 引言
水声学问题主要分为散射、辐射和传播3类, 其中散射问题是最基本的问题[1]。目标声散射一直是水声学领域关注的热点问题, 但由于水声环境的复杂多变, 在应用中仍有许多实际问题有待进一步解决。随着科学技术的发展, 近几十年来目标的声散射问题受到许多工程领域的重视。目标的声散射含有物体的几何形状以及结构组成等重要的信息, 通过对目标散射场的分析, 可以实现对目标物体的侦测以及探伤, 深入研究目标的散射特性是实现目标特征提取和识别的基础, 因此, 目标声散射的研究在实际工程中有十分重要的应用价值。
本文根据前人研究目标声散射场的理论基础[2], 建立了Kirchhoff近似法求解目标声散射场的理想数学模型。借助于MATLAB 软件清晰给出了目标声散射场的仿真图像, 并对此进行了对比分析。
1 基本理论
声散射问题理论上是求解一个数学物理问题, 即求解3D流体空间中的目标受声波激励产生的满足波动方程、表面边界条件和辐射条件的散射声场[3]。目前声散射问题的理论解法主要有: 积分方程方法、-矩阵法、边界法以及分离变量法等[4], 但是所有这些方法的计算都相当繁杂而且难以给出回波结构的物理图象。
Kirchhoff近似法是一种计算声散射回波的物理声学方法。本文将Kirchhoff近似法应用于目标声散射的求解分析, 与其他方法相比, Kirchhoff近似法是计算高频情况下散射和辐射的最常用方法, 虽然这种方法对物理机理的描述有不准确的地方[2], 但是对目标的几何散射特征, 如, 几何亮点特征的描述基本正确, 而几何亮点在多数情况下是回波中的主要亮点, 因此Kirchhoff近似法作为一种工程近似方法仍广泛适用于目标声散射问题中。
2 数学模型
在均匀理想流体媒质中, 小振幅声波声压满足波动方程[5]

考虑图1所示的无限大均匀介质中的刚性球, 平面声波的声压可表示为

式中:0为声压幅值。将式(2)代入波动方程(1)中,
则得到声压满足的赫尔姆荷茨方程

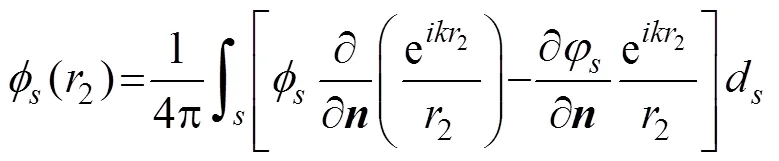
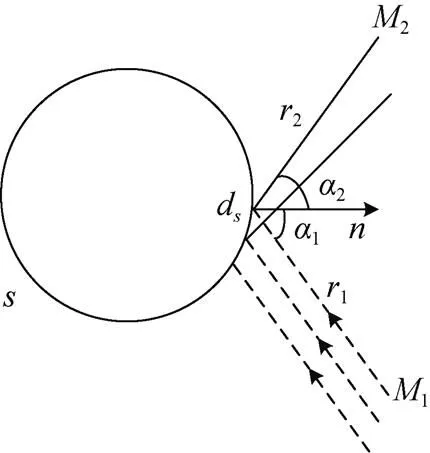
图1 Kirchhoff近似公式推导示意图
因此, 现对Kirchhoff公式作出假设, 以便求得便于计算声散射场的近似解析解, 假设如下。
1) 散射表面的尺寸远大于声波波长, 且其曲率半径也大于波长, 则认为在表面上声压和振动速度近似满足
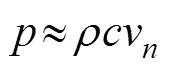
2) 几何影区对散射场的贡献可以忽略。因此实际积分面是从1和2点看去均处在几何亮区的那部分表面0。
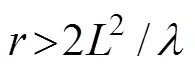
4) 物体表面满足刚性边界条件
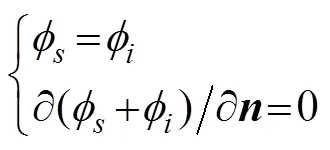

在以上4个假设条件下, 可以导出目标散射势函数

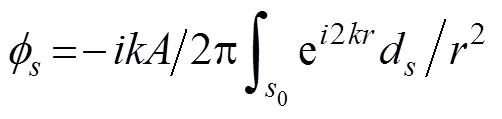
式(9)和式(10)是Kirchhoff近似法求解声散射场的公式, 这两式适用于任何距离。
3 仿真结果与分析

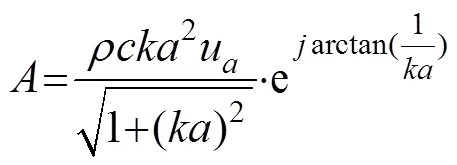
将式(12)代入式(11), 并整理可得

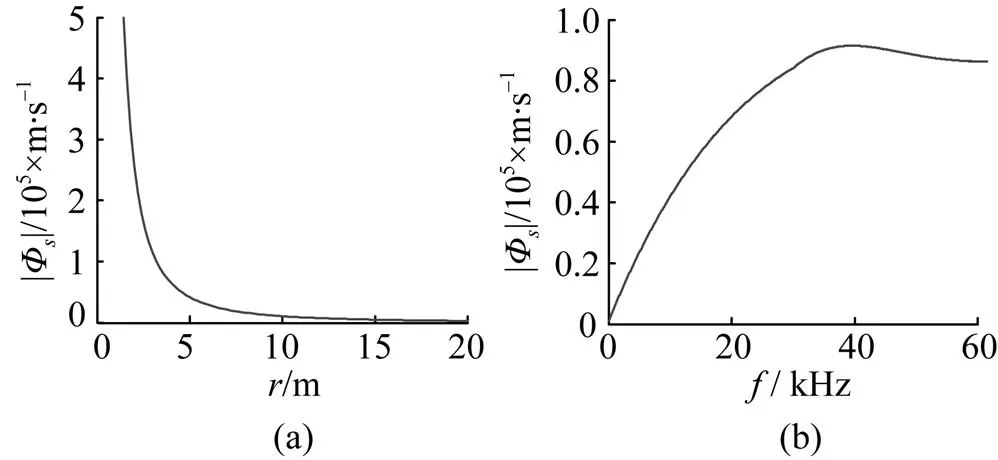
图2 声散射场与距离和频率的变化关系曲线
4 结束语
本文根据前人研究目标声散射场的理论基础,对经典的Kirchhoff公式作一定的假设, 得到收发合置情况下的近似Kirchhoff公式, 进一步对球体目标声散射场进行求解。借助于MATLAB 软件清晰给出了目标声散射场的仿真图像, 并对声散射与作用距离和频率的关系进行了对比分析。从仿真结果可以看出, 目标声散射场随着距离的增加而呈衰减趋势, 随着频率的增加而呈增长趋势, 且其增长或衰减的大小服从指数函数分布, 且当频率增加到一定值时趋于稳定, 这与水声传播相关理论相符。这也可以结合实际加以充分利用, 以满足工程中对水下目标探测与识别的精确需要。
[1] 尤里克 R J. 水声原理[M]. 哈尔滨: 哈尔滨船舶工程学院出版社, 1992: 196-272.
[2] 汤渭霖. 用物理声学方法计算非硬表面的声散射[J]. 声学学报, 1993, 18(1): 45-53.Tang Wei-lin. Calculation of Acoustic Scattering of a Nonrigid Surface Using Physical Acoustic Method[J]. Acta Acustica, 1993, 18(1): 45-53.
[3] 苑秉成, 陈喜. 水声自导原理基础[M]. 北京: 海潮出版社, 1992: 75-80.
[4] 范威, 范军, 陈燕. 浅海波导中目标散射的简正波- Kirchhoff近似混合方法[J]. 声学学报, 2012, 37(5): 475- 483.Fan Wei, Fan Jun, Chen Yan. A Hybrid Normal Modes/ Kirchhoff Approximation Method for Target Scattering in Shallow Water Waveguide[J]. Acta Acustica, 2012, 37(5): 475-483.
[5] 何祚镛, 赵玉芳. 声学理论基础[M]. 北京: 国防工业出版社, 1981: 200-204.
[6] 沈杰罗夫, 水声学波动问题[M]. 北京: 国防工业出版社, 1983: 12-17.
[7] Ross, Tetjana. Acoustic Scattering from Density Sound Speed Gradients: Modeling of Oceanic Pycnoclines[J]. Journal of the Acoustical Society of America, 2012, 131 (1): 54-60.
Simulation of Acoustic Scattering Field of Underwater Targets Based on Approximate Kirchhoff Formula
XIONG Hong-jin1, YUAN Bing-cheng1, ZHAN Hao-ke1, LUO Yin-bo2
(1. Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China; 2. Naval Representative Office in Jiujiang, Jiujiang 332000, China)
Certain assumptions are taken into the classical Kirchhoff formula to obtain an approximate Kirchhoff formula for monostatic array, which is used to solve the acoustic scattering field of spherical targets. As a result, the curve of the acoustic scattering field of spherical targets is achieved by means of MATLAB, and the relations of the acoustic scattering field with the range and incident wave frequency are analyzed. Application indicates that the conclusions drawn from this study are applicable to detection and identification of buried targets underwater.
Kirchhoff approximation method; monostatic array; acoustic scattering field
TP391.9
A
1673-1948(2013)05-0375-03
2013-05-06;
2013-07-11.
国家自然科学基金项目(61074191).
熊宏锦(1987-), 男, 在读博士, 主要研究方向为水下信号与信息处理的研究工作.
(责任编辑: 许 妍)

