直线共轭内啮合齿轮副的啮合效率分析
王郑力, 张振山, 梁伟阁, 张方方
直线共轭内啮合齿轮副的啮合效率分析
王郑力, 张振山, 梁伟阁, 张方方
(海军工程大学 兵器工程系, 湖北 武汉, 430033)
为进一步提高水下航行器热动力装置整体性能, 研究了替代以外啮合齿轮泵作为水下航行器海水泵、燃料泵和滑油泵的内啮合齿轮泵的啮合效率。应用切线极坐标法分析了直线共轭内啮合齿轮副的啮合过程, 以瞬时效率为基础完成了其啮合效率函数的推导, 通过在啮合区间上积分得到平均啮合效率(简称啮合效率)的计算公式,并简要分析了轮齿变形对啮合质量的影响, 以NBX3泵中的齿轮副为例, 对其进行了实例仿真计算, 做出了摩擦系数和传动比对啮合效率的影响曲线, 得出以下结论: 用切线极坐标法分析内啮合齿轮副啮合过程可行且较简便;啮合效率随摩擦系数增大而减小, 摩擦系数越大, 啮合效率下降速率越快; 啮合效率随传动比增大而减小, 与相同参数的渐开线内啮合齿轮副相比, 直线共轭内啮合齿轮副啮合效率更高。
啮合效率; 内啮合齿轮副; 直线共轭
0 引言
啮合效率的高低直接影响齿轮传动的质量, 研究其理论效率不仅对齿轮设计有重要意义, 对磨损机理及泵噪声的分析也具有一定的实用价值。
水下航行器热动力试验结果表明, 其动力装置中的泵是最大的振动噪声源之一, 泵的减振降噪工作亟待开展[1]。研究用内啮合齿轮泵替代原有外啮合齿轮泵作为水下航行器海水泵、燃料泵、滑油泵等, 发挥内啮合齿轮泵具有的输出压力高、结构简单、噪声低等特点, 提高泵的效率, 减小所占空间, 降低噪声, 为进一步提高水下航行器热动力装置整体性能提供有效支撑。
直线共轭内啮合齿轮泵是一种性能优良的容积式泵。该泵采用一对设计新颖的内啮合齿轮副, 其中, 外齿轮(小齿轮)齿廓是左右对称的直线齿廓, 内齿圈(大齿轮)齿廓是与之共轭的曲线[2]。其主要特点为结构紧凑、传动平稳、噪声低, 适用于要求高压、低流量脉动的场合[3]。
文献[4]研究了直线共轭齿廓方程及重合度的计算; 文献[5]分析了滑动系数; 文献[6]给出了切线极坐标法在外啮合齿轮副中的应用方法, 但未对切线极坐标法在内啮合齿轮副中的应用作具体论述; 文献[7]重点分析了渐开线齿轮副的啮合效率。为此, 本文试图应用切线极坐标法分析直线共轭内啮合齿轮副的啮合过程, 以瞬时效率为基础完成其啮合效率函数的推导, 通过在啮合区间上积分得到平均啮合效率的计算公式, 同时, 从齿轮副啮合效率、齿轮啮合冲击及传动运行平稳性3个方面, 简要分析齿轮受载后的弹性形变对啮合质量的影响, 并在MATLAB中对NBX3泵中的齿轮副进行实例计算, 分析摩擦系数和传动比对啮合效率的影响, 从而为直线共轭齿轮副的参数选择和泵性能的提高提供理论依据。
1 直线共轭齿廓传动的啮合点运动
1.1 切线极坐标系

图1 切线极坐标系简图
对于直线共轭齿轮副中的直线齿形, 根据图1(b), 其直线齿廓的切线极坐标方程可写成

1.2 内啮合齿轮副的啮合坐标系

联立式(1)和式(2), 可解得
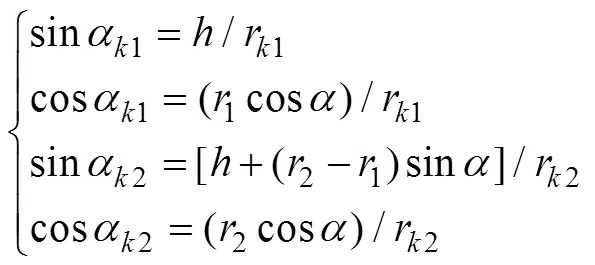
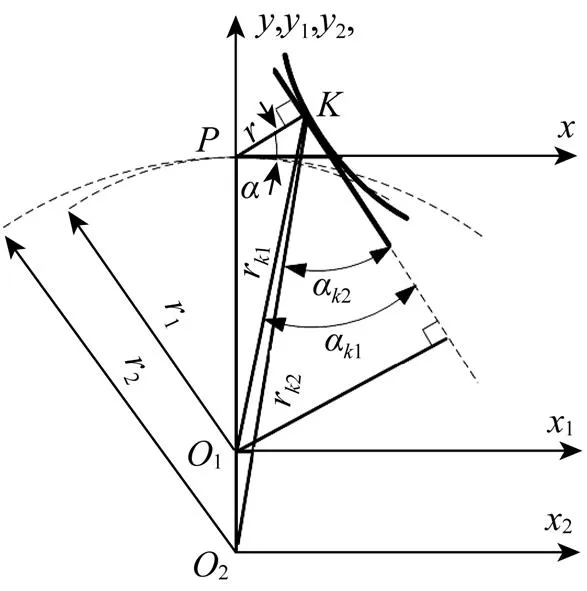
图2 直线共轭内啮合齿轮副啮合简图
2 齿轮副啮合效率分析计算
2.1 齿轮副啮合效率函数

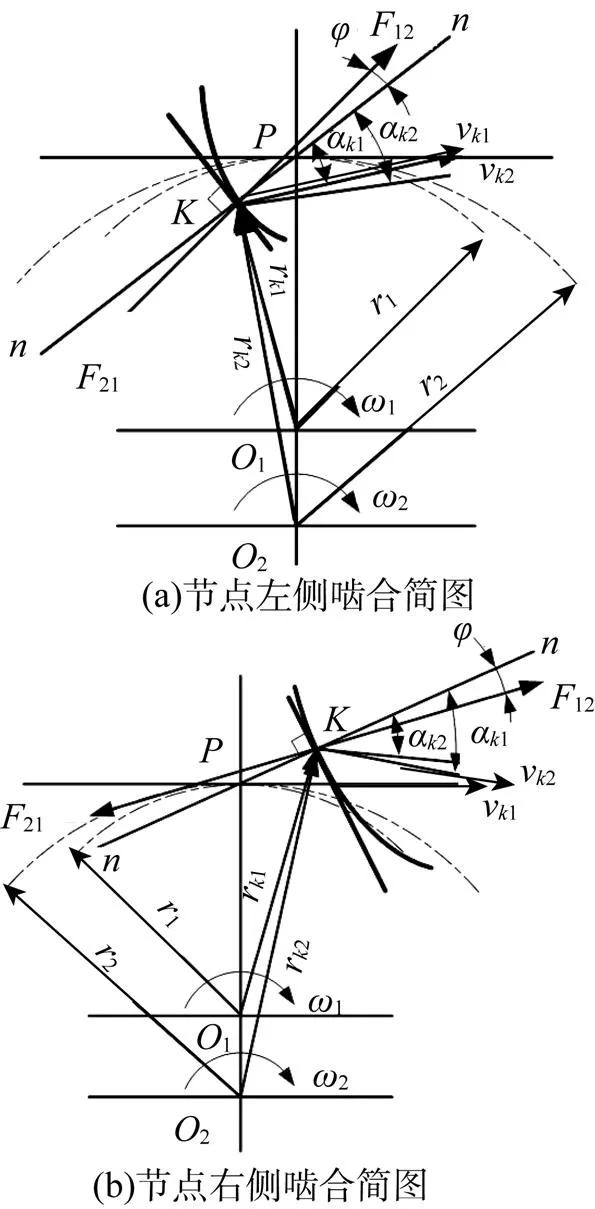
图3 直线共轭啮合分析简图
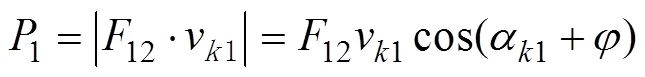
克服工作阻力所需功率为
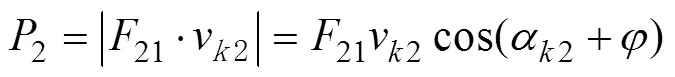

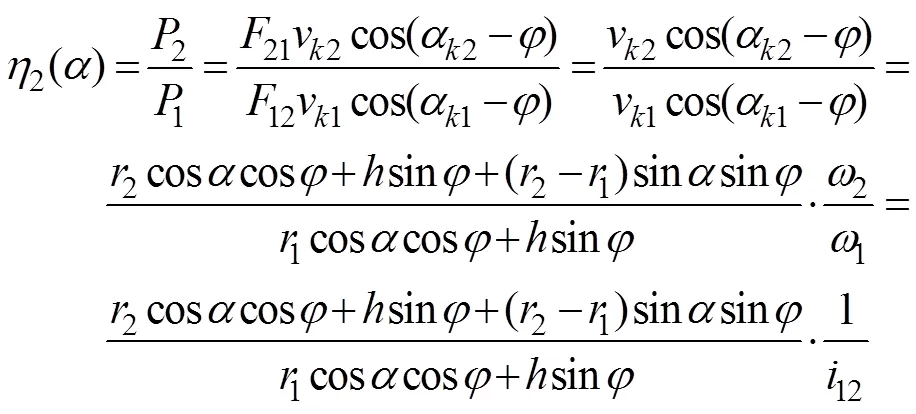
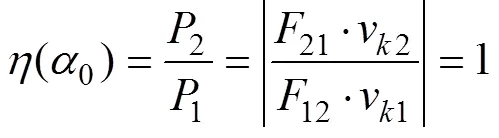
综合式(6)~式(8), 得直线共轭内啮合齿轮副啮合效率函数为
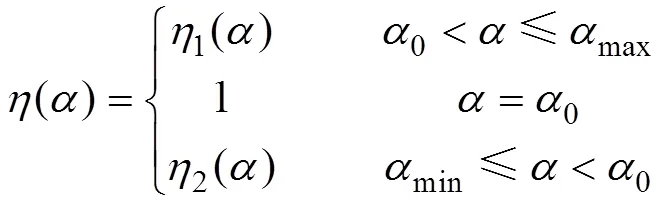

2.2 平均啮合效率
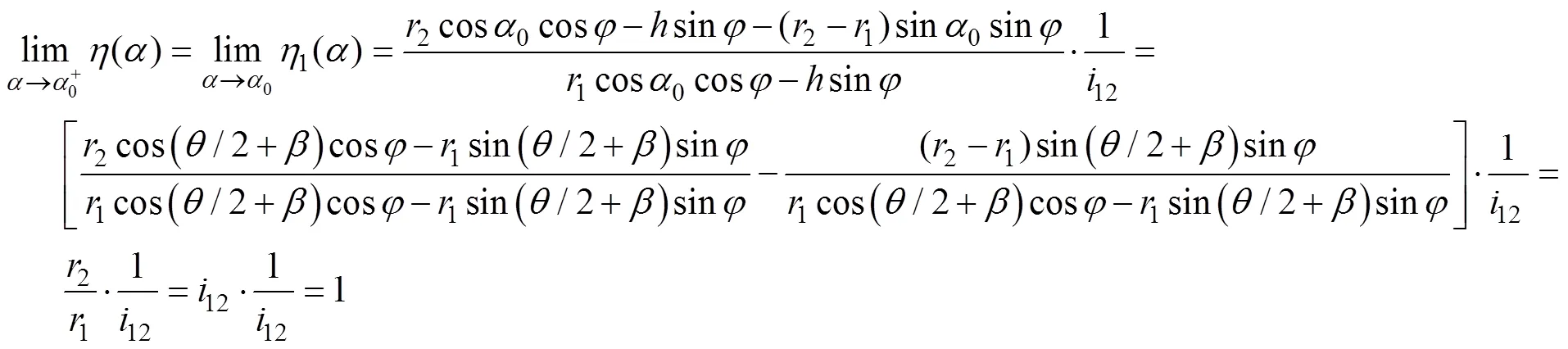


即
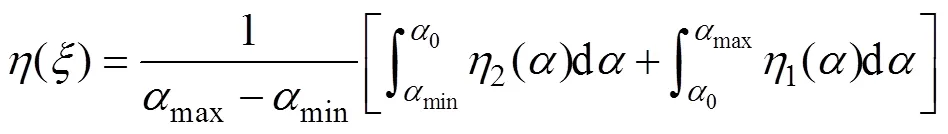
式中积分计算如下
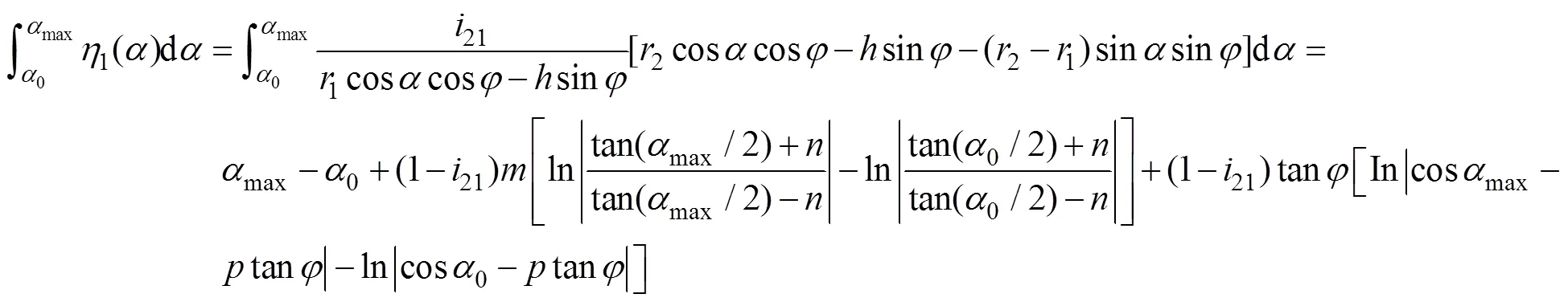
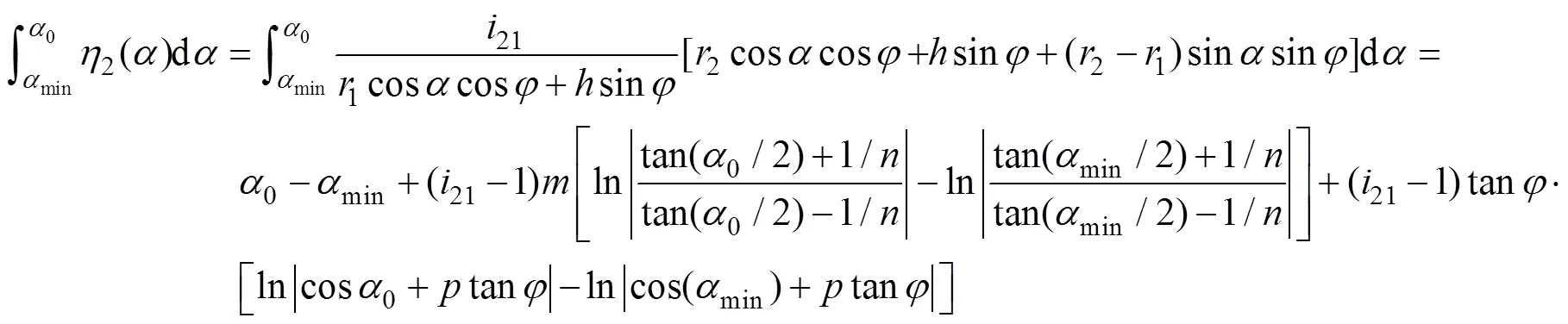
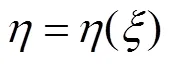
3 齿轮形变
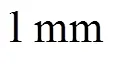


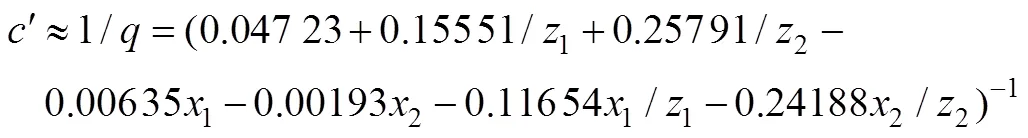

齿轮的总啮合刚度为
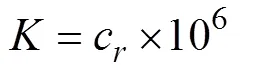
从齿轮啮合冲击及传动运行平稳性方面分析啮合质量, 在齿轮啮合过程中, 由于齿轮的弹性形变引起的刚度激励和啮合冲击是齿轮啮合的主要动态激励之一[8], 对齿轮传动过程中的振动、冲击和噪声有直接影响, 也是影响齿轮传动稳定性、引起参数自激振动的主要因素, 由振动和冲击引起的齿面动载荷, 是影响齿轮副啮合质量及安全可靠性的不利因素。
4 实例
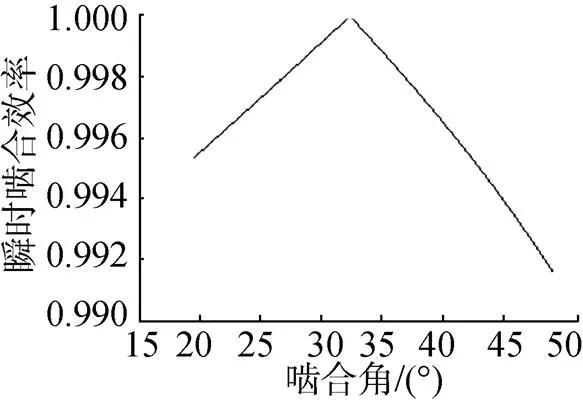
图4 啮合区间内瞬时啮合效率变化曲线
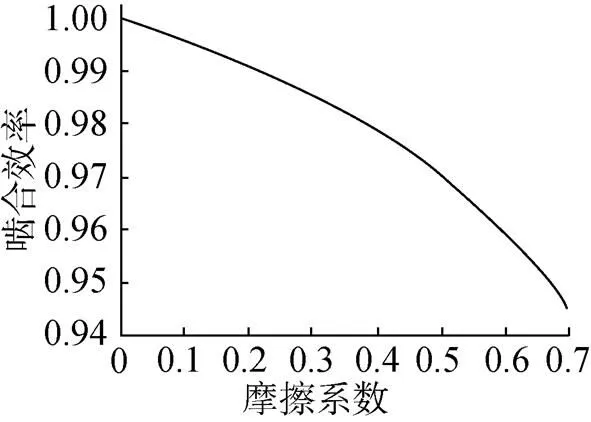
图5 摩擦系数对啮合效率的影响曲线

图6 传动比对啮合效率的影响曲线
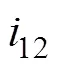
5 结论
本文应用切线极坐标法分析了直线共轭内啮合齿轮副的啮合过程, 以瞬时效率为基础完成了其啮合效率的计算, 通过在啮合区间上积分得到平均啮合效率。以NBX3泵中的齿轮副为例计算了啮合效率, 并做出了摩擦系数和传动比对啮合效率的影响曲线, 通过分析可得出以下结论。
[1] 师海潮. 鱼雷涡轮机动力装置辅机功耗数学模型[J]. 鱼雷技术, 1998, 6(4): 26-31. Shi Hai-chao.The Mathematical Model of Adaptive Power in Auxiliary Power Unit of Torpedo Turbine[J]. Torpedo Technology, 1998, 6(4): 26-31.
[2] Peter G I. Internal Gear Pumps and Their Use in Industry[J]. World Pumps, 1995, 1995(343): 40-41.
[3] Bielmcier E, Bartholomae I, Neveu C D. Measurement of the Temporary Shear Stability of Lubricants in a Gear Pump[J]. Tribo Test, 1999, 6(2): 193-204.
[4] 崔建昆, 秦山, 闻斌. 直线共轭内啮合齿轮副啮合特性分析[J]. 机械传动, 2004, 28(6): 12-15.Cui Jian-kun, Qin Shan, Wen Bin. Study on Meshing Characteristics of Straight Line Conjugate Internal Meshing Gear Pump[J]. Journal of Mechanical Trans- mission, 2004, 28(6): 12-15.
[5] 董永昌, 崔建昆, 李凯, 等. 直线共轭内啮合齿轮副的齿间相对滑动分析[J]. 机械设计与制造, 2006(7): 9-11.Dong Yong-chang, Cui Jian-kun, Li Kai, et al. Study on Sliding Ratio of the Straight Conjugate Internal Gear Pair[J]. Machinery Design & Manufacture, 2006(7): 9-11.
[6] 薛卫东. 研究共轭齿廓曲线的切线极坐标法[J]. 机械
科学与技术, 1994(2): 25-27, 50. Xue Wei-dong. Study on Tooth Profile by Tangent Polar Coordinate[J]. Mechancal Science and Technology, 1994 (2): 25-27, 50.
[7] 姚建初, 陈义保, 周济, 等. 齿轮传动啮合效率计算方法的研究[J]. 机械工程学报, 2001, 37(11): 18-21, 27.Yao Jian-chu, Chen Yi-bao, Zhou Ji, et al. Study on a Method for Calculating Gearing Meshing Efficiency[J]. Chinese Journal of Mechanical Engineering, 2001, 37(11): 18-21, 27.
[8] 朱孝录, 鄂中凯. 齿轮承载能力分析[M]. 北京: 高等教育出版社, 1992.
[9] 李茹贞, 赵清慧. 齿轮强度设计资料[M]. 北京: 机械工业出版社, 1984.
[10] 赵东升, 汪中厚, 张立平, 等. 渐开线直齿圆柱齿轮的刚度精密分析方法及其影响因素探讨[J]. 机械传动, 2010, 34(4): 24-27.Zhao Dong-sheng, Wang Zhong-hou, Zhang Li-ping, et al. A Precise Analytical Method of the Stiffness of Involute Spur Gear and Exploration of the Influencing Factors of Stiffness[J]. Journal of Mechanical Transmission, 2010, 34(4): 24-27.
[11] 张展, 朱景梓, 秦立高. 渐开线内啮合圆柱齿轮传动[M]. 北京: 国防工业出版社, 1997.
Analysis on Meshing Efficiency of Straight Conjugate Internal Gear Pair
WANG Zheng-li, ZHANG Zhen-shan, LIANG Wei-ge, ZHANG Fang-fang
(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)
To improve the performance of thermal power as a whole for an underwater vehicle, the meshing efficiency of straight conjugate internal gear pair, which substitute for external gear pair of sea water pump, fuel pump and lubricating oil pump for an underwater vehicle, is investigated, the meshing characteristics of straight conjugate internal gear pair are analyzed on the basis of tangent polar coordinate, and a meshing efficiency function is derived based on the instantaneous efficiency. Moreover, a formula for calculating the average meshing efficiency(short for meshing efficiency) is obtained through integrating in the meshing interval, and the influence of gear deformation on meshing quality is analyzed. Taking the gear pair in NBX3 pump for example, the curves of friction coefficient and gear ratio versus meshing efficiency are simulated, and the following conclusions are drawn: 1) tangent polar coordinate is feasible and convenient for analyzing the meshing characteristics of the internal gear pair; 2) meshing efficiency decreases with the increase in friction coefficient, and the decreasing rate of meshing efficiency accelerates with increasing friction coefficient; 3) meshing efficiency decreases with the increase in gear ratio, and the straight conjugate internal gear pair gets higher meshing efficiency than involute internal gear pair.
meshing efficiency; internal gear pair; straight conjugate
TJ630.32
A
1673-1948(2013)05-0369-06
2013-04-08;
2013-05-10.
部级国防科技基金资助项目(4011002010302).
王郑力(1989-), 男, 在读硕士, 主要研究方向为兵器发射与动力推进技术.
(责任编辑: 陈 曦)

