一种考虑时钟同步问题的多AUV协同定位算法
张福斌, 张小龙, 马 朋
一种考虑时钟同步问题的多AUV协同定位算法
张福斌, 张小龙, 马 朋
(西北工业大学 航海学院, 陕西 西安, 710072)
在多自主水下航行器(multi-AUVs)协同导航系统中, 领航AUVs配备高精度导航定位设备, 跟随AUVs配备低精度导航设备, 领航、跟随AUVs均配备水声通信设备, 跟随AUVs利用领航AUVs的广播信息获得其与领航者间的距离。本文针对领航AUVs与跟随AUVs间的时钟不同步问题, 给出了AUV时钟相对偏移与相对漂移模型, 并将跟随AUVs的时钟偏差作为未知量, 提出了一种考虑时钟同步问题的multi-AUVs协同定位算法。仿真结果表明, 该算法不仅可以大幅度提高跟随AUVs的协同定位精度, 而且能够随时对跟随AUVs时钟误差进行估计, 有效地提高了multi-AUVs协同导航系统性能。
多自主水下航行器; 时钟同步; 协同导航
0 引言
在多自主水下航行器(multiple autonmous un- derwater vehicles, multi-AUVs)协同导航定位系统中, 利用水声通信技术测量AUVs间相对位置关系, 提高系统整体定位精度, 已成为国内外AUV导航定位领域重点研究的问题。
2005年, Curcio等利用时间同步信号和水声传播延迟的方法进行了相对位置测量, 对1个领航者、2个跟随者进行了试验, 并进行了误差分析[1]; Bahr等应用卡尔曼滤波对领航-跟随式多AUV协同定位方法进行了研究, 并进行了试验验证[2]。2008年, 张立川等在测量水声传播延迟的条件下, 对多AUV协同导航算法进行了研究[3]; Yao Yao等研究了多AUV间的位置关系对协同定位精度的影响[4]。
由于水下AUVs间通信频带受限的特点, 同时为了降低AUV功耗, 提高数据更新速率, 一般采取单向水声通信测距(one way travel time, OWTT)的模式[5-6]。单向测距法要求所有AUV内部时钟时刻保持同步, 虽然AUV出航前可通过GPS授时的方式实现, 但随着时间的增加, AUV内部时钟必然会产生漂移, 从而对水声测距精度造成影响, 进而影响AUV的定位精度。
AUVs间的时钟同步包括: 领航AUVs间的时钟同步和领航、跟随AUVs间的时钟同步2个方面。领航AUVs由于数量少, 内部时钟精度较高, 故可采取双向水声通信方式实现之间的时钟同步; 而跟随AUVs数量一般较多, 内部时钟精度较低, 如果仍采用领航AUVs间的时钟同步方法, 由于受水下通信带宽较窄等因素制约, 实现困难。本文针对多AUV协作系统中跟随AUVs随着航行时间增加出现的时钟不同步问题, 给出了跟随AUVs时钟相对偏移与相对漂移模型, 并将AUVs间时钟差作为未知量带入定位方程, 利用非线性加权最小二乘算法进行求解。最后通过数学仿真试验验证了算法的有效性。在多AVU协同定位系统中, 领航AUVs间也存在时钟同步问题, 但非本文研究重点, 则另文重点分析。
1 时钟模型
AUV时钟通常是利用晶体振荡器脉冲来度量[7], 即

在多AUV协同过程中, 即使AUVs间时钟误差不大, 但是经过与水下声速的相乘, 也会产生很大的测距误差, 影响AUVs协同定位精度, 因而AUVs间的时钟同步在利用OWTT法进行协同定位的过程中必须加以考虑。
2 AUVs间时钟同步
AUVs间时钟同步过程中, 并不要求AUV时钟均与标准物理时钟相同步, 而是要求各AUVs间时钟保持一致, 即可认为AUVs间时钟是同步的。假定c()为AUV领航时钟,c()为AUV跟随时钟,c()为标准物理时钟, 从而有
领航AUVs时钟

跟随AUVs时钟

则领航AUVs时钟与跟随AUVs时钟差
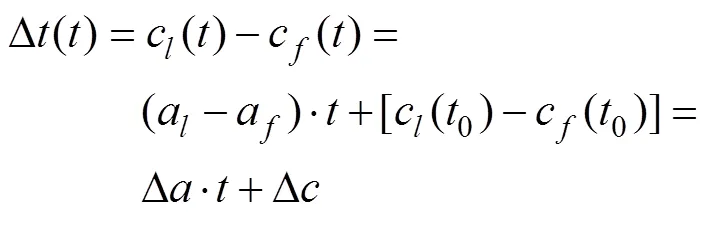
从式(5)可知, 领航AUVs时钟与跟随AUVs时钟差既有因初始时刻不同步而产生的相对偏移, 又有因晶振频率不同而产生的相对漂移。然而, 在多AUV协同过程中, 不论AUVs间时钟存在相对偏移还是相对漂移, 均可将其时钟差作为一整体未知量加以考虑。
3 时钟同步的多AUV协同定位算法
AUVs协同定位过程中, 由于AUV深度状态可利用深度传感器直接精确测得, 3D运动模型通过在水平面内投影可转化为2D运动模型, 因此为得到AUV位置状态只需确定其经度、纬度信息。再考虑作为未知量的领航AUVs与跟随AUVs间时钟差, 可知在利用非线性加权最小二乘算法进行协同定位计算过程中, 所需确定的未知量共有3个(经度、纬度和时钟差), 为了保证定位方程可解, 则需从3个或3个以上领航AUVs处获得距离量测信息。对于1个或2个领航AUVs构成的协同定位系统, 可利用构建虚拟基点的方法进行求解[9]。
本文假设领航AUVs间已实现时钟同步, 领航AUVs与跟随AUVs保持图1所示队形(跟随AUVs处在3个领航AUVs构成的等边三角形中心)。

图1 多自主水下航行器协同定位队形示意图
在利用OWTT进行多AUV协同定位过程中, 利用领航、跟随AUVs间水声信号的单程传播延时即可获得AUVs间的相对距离量测值。若领航AUVs和跟随AUVs间时钟同步, 即两时钟同频同相, 或已知相差, 则可得领航、跟随AUVs间的量测距离


(8)


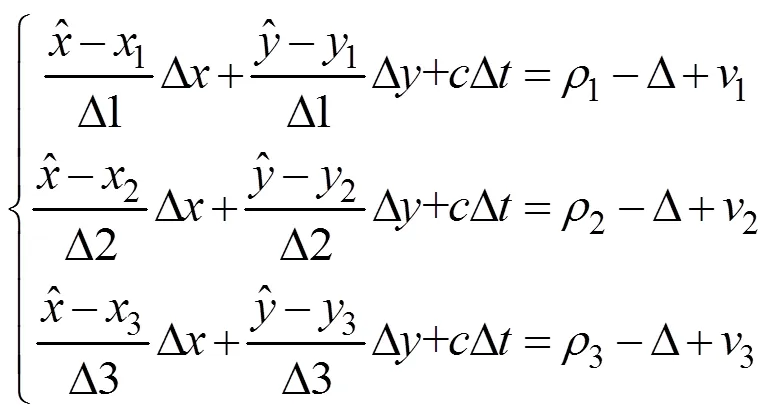

式中

实现跟随AUVs自定位位置的实时修正。
4 仿真结果与分析
为了验证协同定位算法的有效性, 进行系列仿真试验。在下述试验中考察由4个AUVs组成的协同定位编队, 领航、跟随AUVs均做2D平面运动, 其运动队形如图1所示。仿真设置如下。
图中给出了AUVs运动轨迹、跟随AUV的定位轨迹、跟随AUV经过修正后的协同定位误差、跟随AUV时钟误差的计算情况。从图中可以看出, 跟随AUV在自定位存在较大误差的情况下, 通过利用领航AUVs进行协同定位, 可以获得较高的定位精度。

图3 时钟偏移下的仿真结果

图4给出了多AUV运动轨迹、跟随AUV的定位轨迹、跟随AUV经过修正后的协同定位误差以及同时存在相对偏移和相对漂移下的AUV时钟误差估计与估计误差。从图中可以看出, 当相对偏移量和相对漂移量同时存在时, 跟随AUV同样可以获得比较准确的定位精度。
由以上2次仿真结果得出, 无论AUVs间时钟存在相对偏移还是相对漂移, 在将时钟误差作为未知量进行考虑时, 本文所设计算方法不仅可以得到理想的协同定位精度, 而且能够随时对AUVs间时钟误差进行估计与修正, 有效地提高了AUVs协同定位效能。

图4 时钟偏移及漂移下的仿真结果
5 结束语
本文针对多AUV协同定位系统中AUVs间时钟不同步问题, 建立了AUVs时钟同步模型, 将时钟差作为未知量, 设计了基于加权最小二乘的AUVs协同定位算法, 最后进行了仿真验证。仿真结果表明, 所提算法可以有效地对AUVs间时钟误差进行估计及修正, 提高了多AUV协同定位精度。
[1] Curcio J, Leonard J, Vaganay J, et al. Experiments Inmo- ving Baseline Navigation Using Auto-nomous Surface Craft[C]//Proceedings of the 2005MTS/IEEE Oceans Co- nference. IEEE, 2005: 730-735.
[2] Bahr A, Leonard J J. Cooperative Localization for Auton- mous Underwater Vehicles[C]//In Proceedings of the10th International Symposiumon Experimental Robotics(ISER), 2006: 1-10.
[3] 张立川, 刘明雍, 徐德民, 等. 基于水声传播延迟的主从式多无人水下航行器协同导航定位研究[J]. 兵工学报, 2009, 30(12): 1674-1678.Zhang Li-chuan, Liu Ming-yong, Xu De-min, et al. Co- operative Localization for Multi-UUVs Based on Time-of- flight of Acoustic Signal[J]. Acta Armamentarii, 2009, 30 (12): 1674-1678.
[4] Yao Y, Xu D M, Yan W S, et al. An Optimal Measure Choosing Strategy to AUVs Cooperative Localization[C] //Proceedings of 4TH IEEE Conference on Industrial Electronic and Application(ICIEA), 2009: 1889-1894.
[5] Eustice R, Whitcomb L, Singh H, et al. Experimental Results in Synchronous-Clock One-Way-Travel-Time Acoustic Navigation for Autonomous Underwater Vehi- cles[C]//IEEE International Conference on Robotics and Automation, IEEE, 2007: 4257-4264.
[6] Eustice R, Whitcomb L, Singh H, et al. Recent Advances in Synchronous-Clock One-Way-Travel-Time Acoustic Navigation[C]//Proceedings of the 2006 IEEE/MTS Oce- ans Conference, IEEE, 2006: 1-6.
[7] 任丰原, 董思颖, 何滔, 等. 基于锁相环的时间同步机制与算法[J]. 软件学报, 2007, 18(2): 372-380.Ren Feng-Yuan, Dong Si-Ying, He Tao, et al. A Time Synch- ronization Mechanism and Algorithm Based on Phase Lock Loop[J]. Journal of Software, 2007, 18(2): 372-380.
[8] 张先富, 冯冬芹. 基于加权最小二乘法的精确时钟同步算法研究与实现[J]. 传感技术学报. 2008, 21(3): 1556-1560.Zhang Xian-fu, Feng Dong-qin. Realization of Precise Time Synchronization Algorithm Based on Weighted Least-Squares Algorithm[J]. Chinese Journal of Sensors and Actuators, 2008, 21(3): 1556-1560.
[9] 马朋. 基于广播通信的多AUV协同定位技术研究[D]. 西安: 西北工业大学, 2013.
An Algorithm of Multi-AUVs Cooperative Location Considering Clock Synchronization
ZHANG Fu-bin, ZHANG Xiao-long, MA Peng
(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)
In the multi-AUVs cooperative navigation system, the leader AUVs are equipped with high-precision navigation and location equipments, the follower AUVs are equipped with low-precision navigation equipments, the leader AUVs and the follower AUVs are all equipped with underwater acoustic modem, and the follower AUVs use the broadcast information from the leader AUVs to obtain the distance to the leader AUVs. This paper aims at the clock asynchrony between the leader and follower AUVs to establish a relative offset model and a relative drift model of AUV clock. By taking the clock offset of a follower AUVs as unknown variable, a multi-AUVs cooperative location algorithm considering clock synchronization is proposed. Simulation results show that the algorithm can greatly improve the location accuracy of the follower AUVs and estimate the clock error of the follower AUVs at any time, thus enhance the performance of the multi-AUVs cooperative navigation system effectively.
multiple autonomous underwater vehicle; clock synchronization; cooperative navigation
TJ630.33; TP391
A
1673-1948(2013)05-0355-05
2013-04-02;
2013-05-22.
国家自然科学基金(6127333).
张福斌(1972-), 男, 博士, 副教授, 主要研究方向为水下航行器导航与控制技术.
(责任编辑: 杨力军)

