集装箱正面吊曲臂的有限元分析及优化
祖海英,赵伟民,韩佳轩
(1.东北石油大学机械科学与工程学院,黑龙江 大庆 163318)
随着全球集装箱运输持续快速增长,码头或中转站集装箱堆场容量的需求也相应增大.集装箱正面吊广泛应用于集装箱货场、中转站和码头等物流装卸场所[1],按其吊臂的结构形式分为直臂和曲臂,其中直臂正面吊具有简单、截面小、自重轻等优点,但是直臂不能跨箱作业,致使工作效率较低;而曲臂正面吊不仅可以跨箱作业并能直接吊运船上的集装箱,效率高且具有良好发展前景.本文通过借鉴利勃海尔曲臂正面吊的技术参数,建立分析模型并进行相关的分析研究.
1 曲臂正面吊的作业分析
曲臂正面吊如图1所示:由底盘、变幅油缸、基本臂、伸缩臂、集装箱吊具、伸缩油缸、摆动油缸等组成.
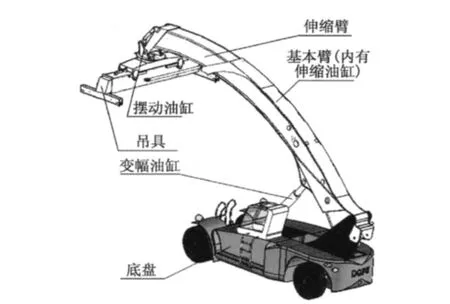
图1 整体分析模型Fig.1 Model of analysis while-machine
曲臂正面吊的吊臂为两节液压伸缩臂,可以实现无级伸缩和带载伸缩[2].曲臂正面吊可以实现跨箱作业,它可以在第1 排的4 层箱不移动的情况下,直接将第2 排的第4 层箱取走;在不移动第1、2排的3 层箱的情况下,直接将第3 排第3 层箱取走;这样就大大减少了移动的次数并提高效率.工作示意图如图2所示,a,b,c,d 表示其跨箱作业的过程.集装箱正面吊在换用不同吊具时,还可实现整体的吊装.吊轻箱时,还可纵向吊箱.集装箱正面吊的吊具可±180°旋转,横移量为±200 mm,装卸对箱时只需操纵曲臂和吊具,而不用移动整车,生产率可达38 标准箱·h-1.

图2 跨箱作业示意图Fig.2 Sketch map for span working
2 曲臂正面吊的工况运动分析[3]
曲臂正面吊有如下三种工况:
(1)吊第1 排第5 层,箱重为45 t,吊臂处于最大载荷于工作最高点.
(2)吊第2 排第4 层,跨箱作业,箱重为38 t,吊臂处于力矩最大点.
(3)吊第3 排第3 层,跨箱作业,箱重为30 t,吊臂处于最远工作点.
以上三种工况是曲臂正面吊在工作中可能产生危险的情况,因此下面将对这三种工况进行运动学研究.
运动分析时曲臂正面吊的运动副设置:以基本臂的后铰耳与车体连接处的运动副为旋转副,以变幅油缸与基本臂上铰耳连接处的运动副为旋转副,以变幅油缸缸筒与变幅油缸杠杆的运动副为同心移动副,以变幅油缸与车体前铰耳连接处的运动副为旋转副,以基本臂与伸缩臂的4 个接触面的运动副为移动副,以吊具与伸缩臂下铰耳连接处为旋转副.
吊臂的运动方式:变幅与伸缩同步进行,设变幅与伸缩油缸的运动为匀速运动.吊臂将集装箱从地面吊到第1 排第5 层的位置,然后将其放到第4层箱上面.
仿真时间设置为120 s,工况1 的计算结果如图3所示.基本臂的后铰耳与车体连接处(A点)反作用力曲线如图3a 所示,油缸与基本臂上铰耳连接处(B点)反作用力曲线如图3b 所示,吊具与伸缩臂铰耳连接处(C点)作用力曲线如图3c 所示.
从图3曲线可知,当吊臂在运动初始位置时,A,B,C点处的反作用力幅值最大,因为此时吊重在x方向距离A点最远,产生的力矩也最大,B点处的反作用力也相应最大.采用同样的方法对工况2,3进行运动分析,得到三种工况下A,B,C三点的对比,见表1.从表1中可看出工况1 为最危险工况.
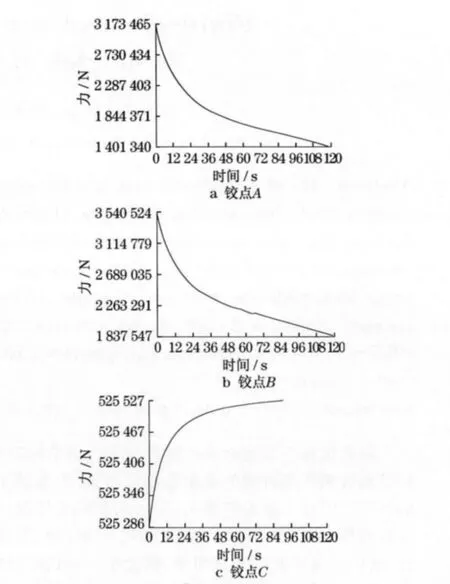
图3 铰点 A,B,C 的作用力Fig.3 Force of hinge A,B,C
3 正面吊曲臂的有限元分析
曲臂的支承情况:水平销轴将下铰耳与底盘连接,在变幅平面内自由转动,在基本臂前半部下面支承变幅油缸.该单变幅液压缸位于吊臂中线,支承处可视作处于圆柱体上的约束,使其在横向对吊臂不施加约束.吊臂由4 块钢板焊接组成,上下各一个弯曲翼板,左右各一个矩形截面的圆弧腹板,其翼板较腹板厚.吊臂的伸缩机构采用一级伸缩缸[4].
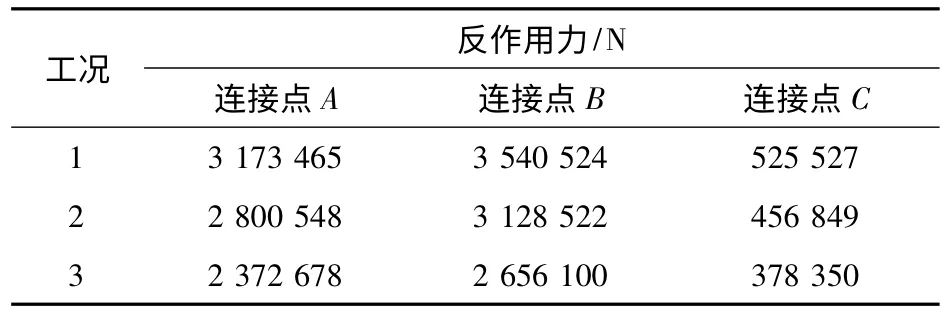
表1 结果对比表Tab1 Contrust of simulation results
3.1 工况1下曲臂结构有限元分析
考虑吊臂的自重,为确保其重心位置的准确性,需以吊臂的实际工况位置进行建模,由于基本臂及伸缩臂结构复杂且刚性很大,故将其简化成2个实体建模,基本臂与伸缩臂选材均为40 MnVB.
取运动学分析中工况1 下的最大反作用力的载荷来计算.在基本臂尾部与车体铰接处,约束3个方向平行自由度(Ux,Uy,Uz)和两个方向的转动自由度(Ry,Rz),释放绕销轴中心回转的转动自由度(Rx).变幅液压缸与基本臂相联接的铰点处作同样处理.两节臂之间搭接处理为面接触,只释放其轴向转动自由度.
根据《起重机设计手册》,臂允许的位移变形量为
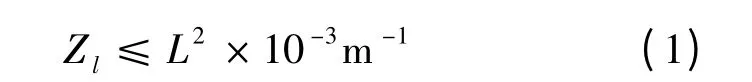
由式(1)得Zl≤0.306 m,L为臂长,L=17.5 m.
位移最大变形量Umax=0.262 m,在允许范围内;最大应力发生在伸缩臂的末端与基本臂连接的变截面处,应力值达到 634 MPa.由于基本臂前端的面积较小,受到来自伸缩臂下翼板的压力,产生了应力集中;在变截面处截面尺寸突然变小,造成该处的应力增大;基本臂上翼板处的臂为薄板,所以产生较大的应力.材料许用屈服强度为
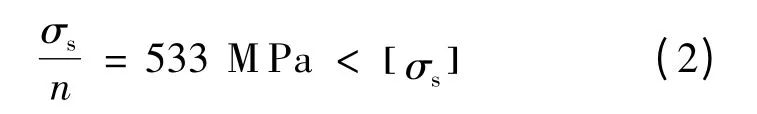
式中:材料的屈服强度为σs=800 MPa,允许屈服强度 [ σs]=634 MPa,安全系数取n=1.5.
通过对上述有限元模型进行分析,如图4所示,得到在工况1 下的位移最大变形量发生在吊臂头部,位移量为0.262 m,小于允许的最大位移变形量0.306 m.最大应力如图5所示,发生在伸缩臂末端与基本臂连接的变截面处,最大当量应力值达到634 MPa,大于许用屈服强度533 MPa,因此设计不合理.
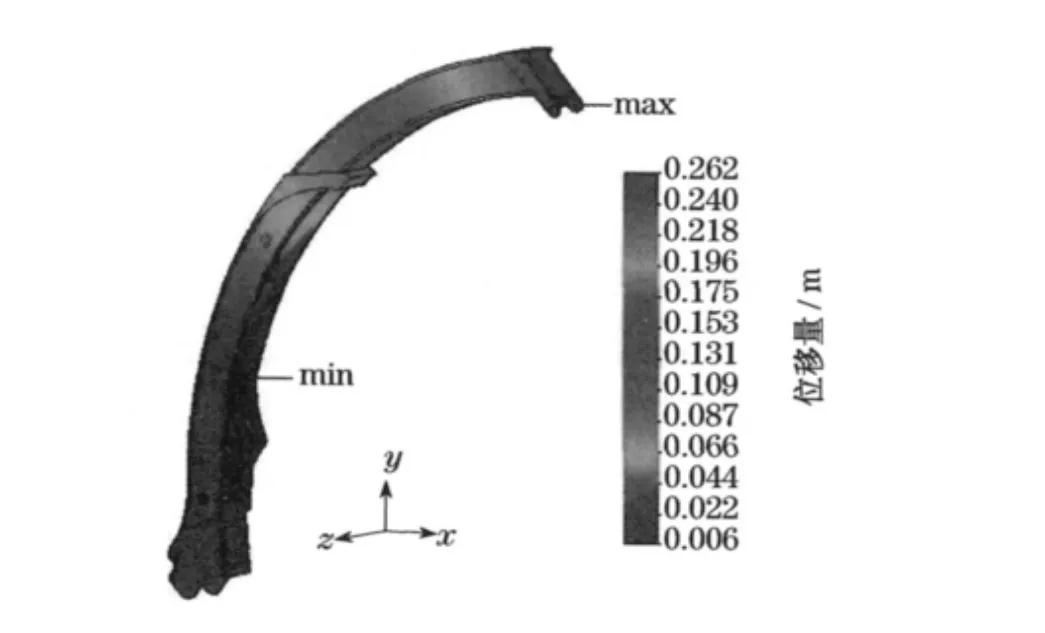
图4 合力位移云图Fig.4 Displacement cloud picture
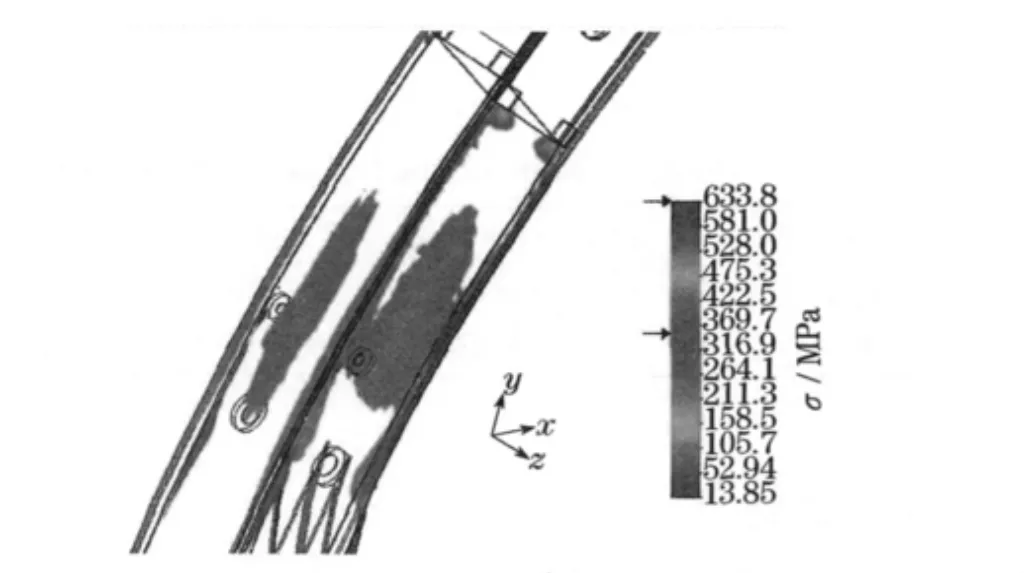
图5 截面应力云图Fig.5 Stress of section cloud picture
3.2 工况2下曲臂结构有限元分析
加载为工况2 下的最大反作用力时的载荷,得到在工况2 下的位移最大变形量位于吊臂头部,值为0.295 m,小于允许的位移变形量0.345 m.最大当量应力发生在伸缩臂末端与基本臂连接处,其值为446 MPa,小于许用屈服强度 533 MPa,设计合理.
3.3 工况3下曲臂结构有限元分析
加载为工况3 下的最大反作用力时的载荷,得到在工况3 下的位移最大变形量位于吊臂头部,值为0.280 m,小于允许的位移变形量0.349 m.最大当量应力发生在伸缩臂末端与基本臂连接处,其值为418 MPa,小于许用屈服强度533 MPa,设计合理.
4 正面吊曲臂的人工优化
4.1 曲臂的形状参数优化
通过对以上曲臂的有限元分析结果显示:曲臂高应力区发生在基本臂下翼板滑块处、伸缩臂上翼板滑块处、伸缩臂下末端与基本臂的接触截面突变处、基本臂截面突变处以下的上下翼板至变幅油缸铰点之间的区域.相对应力较小的区域为:伸缩臂的上下翼板及左右腹板.对其进行直接人工优化:对于结构强度不足处进行结构加强;对于结构强度较高的区域考虑适当减小其厚度[5].
4.2 曲臂优化前后的有限元分析
通过对最危险的工况1 进行有限元分析,施加载荷取自运动学分析中的结果.通过有限元进行计算,得到在工况1 下的位移最大变形量位于吊臂头部,为 0.280 m,在允许范围 0.306 m 内.应力计算结果与优化前对比如表2所示,最大应力发生在基本臂油缸铰耳的4 个侧板与基本臂下翼板连接处,其值为455 MPa,小于许用屈服强度533 MPa,达到优化目的.

表2 吊臂优化对比表Tab.2 Contrast table of the lift arm optimiztion
5 结论
本文分析设计了45 t 集装箱曲臂正面吊,对曲臂正面吊进行了运动学分析和有限元分析,同时对其结构进行了人工优化分析.优化后,最大应力减少了28.2%,最大位移增加了6.87%,最大应变减少了25.7%,整个吊臂质量减少了12.3%.且优化后最大应力与最大位移均在许用应力与许用位移范围之内.
[1]范恒满.集装箱正面吊运起重机试验体系研究[J].起重运输机械,2012(7):89-91.FAN Hengman.Research on the test system of container reach stacker[J].Lifting the Transport Machinery,2012(7):89- 91.
[2]张奇生,王益群,任光合.某集装箱正面吊大臂举升关键技术研究[D].秦皇岛:燕山大学,2012.ZHANG Qisheng,WANG Yiqun,REN Guanghe.The key technology research for a researcher big arm lifting[D].Qinhuangdao:Yanshan University,2012.
[3]ANANTHASURESH G K.Design of fully rotatable,roller-crankdriven,cam mechanisms for arbitrary motion specifications[J].Mechanism and Machine Theory,2001,36:448-452.
[4]周齐齐,袁正,常亮.重箱吊具力学性能有限元分析与研究[J].机械工程师,2011(5):76-78.ZHOU Qiqi,YUAN Zheng,CHANG Liang.Analysis and research on heavy box sling mechanical properties of finite element[J].Mechanical Engineer,2011(5):76- 78.
[5]WU Jiajang.Finite element modelling and experimental modal testing of a three dimensional framework [J].International Journal of Mechanical Sciences,2004,46(8):1245-1266.

