基于两参数威布尔分布的设备可靠性预测研究
徐 微,胡伟明,孙 鹏
(1.北京天泰志远科技有限公司,北京 100029;2.中国石油塔里木油田塔西南勘探开发公司柯克亚作业区轮南项目部,新疆库尔勒 841000)
现代机械设备正不断向自动化、高速化、复杂化等方向发展,一旦其中某部件发生故障,将直接影响整个机械设备的正常运行,所以在故障发生前进行可靠性预测,有助于设备安全性的提高,维修成本的降低,企业管理水平的提升.
威布尔分布作为一种可靠性模型,已在很多领域内得到了不同程度的发展[1].但关于威布尔分布的参数估计,尽管前人已有了大量的研究成果,但在工程实际中仍较难得到应用,如温艳清等人利用Newton-Raphson(牛顿迭代)算法以及完整数据的极大化(CM)算法成功实现了其参数估计[2],但该方法计算繁琐且理论性较强,使得工程上应用困难,而方华元等人则在极大似然法的基础上进行了改进,提出了遗传算法的优化[3],这种方法虽然提高了精度,但是由于遗传算法是一种随机的选择,导致了其结果有一定的波动,因此,考虑到这些理论的复杂性,工程实施中的难度性,本文提出了比较简洁且易于观察的最小二乘法——水平残差和垂直残差平方和最小两种方法对模型的参数估计,只要在普通坐标纸上画出经变化后的失效时间的变换x、累积函数的变换y值或在威布尔概率坐标纸上直接画出失效时间t、累积函数F(t)的原始数据,即可完成参数的估算,从而实现工程中设备或部件的可靠性预测.
1 形状、尺度参数威布尔分布模型
威布尔的概率密度函数为

式中:m为反映不同时期故障率曲线形状的参数;n为衡量平均故障间隔时间的尺度参数;r为寿命极限值或最小值的位置参数,该值是否取零与模型参数个数有关.
考虑到三参数威布尔分布模型的复杂结构,计算的繁琐以及在实际工程中的较少应用,因此本文采用简化后的两参数威布尔分布模型,并利用最小二乘法对设备或部件的可靠性进行预测研究[4].
二参数威布尔分布的密度函数、失效率函数、累积分布函数及可靠度函数分别见图1—图4.从图中可以看出,形状参数m值的不同获得的曲线形状有很大区别.

图1 二参数威布尔分布的密度函数Fig.1 Probability density function of two parameters Weibull

图2 二参数威布尔分布的失效率函数Fig.2 Failure rate function of two parameters Weibull

图3 二参数威布尔分布的分布函数Fig.3 Cumulative distribution function of two parameters Weibull
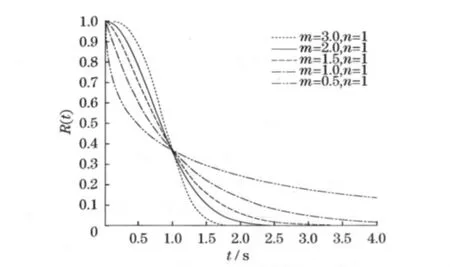
图4 二参数威布尔分布的可靠度函数Fig.4 Reliability function of two parameters Weibull
2 威布尔最小二乘估计
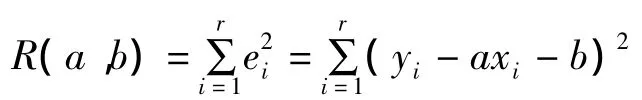
两参数威布尔的累积分布函数可以表示为
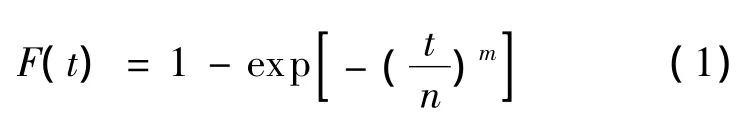
对等式两边进行变换后则有

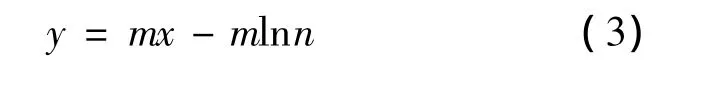
2.1 垂直残差平方和最小拟合数据点的最小二乘法(方法1)
形状、尺度参数计算公式可以表示为
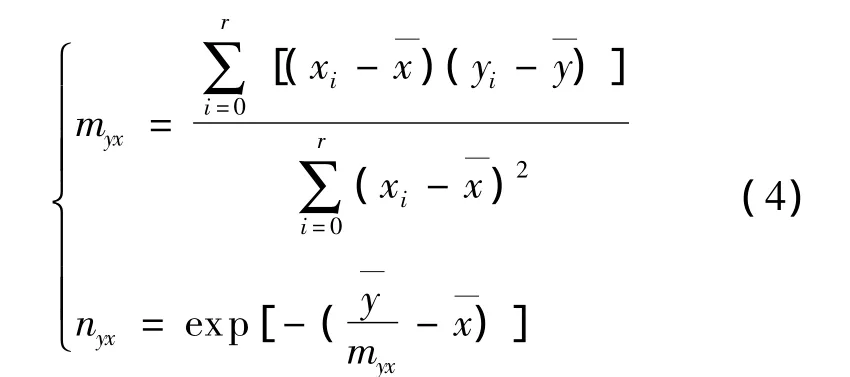
垂直残差平方和为

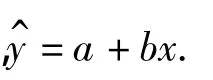
2.2 水平残差平方和最小拟合数据点的最小二乘法(方法2)
形状、尺度参数计算公式可以表示为

水平残差平方和为


结合式(5)和式(7)可得
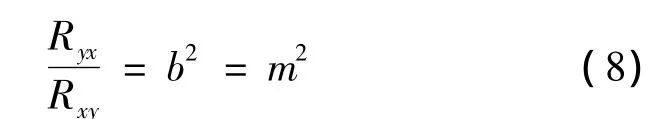
综上,若残差系数m>1时,则用水平残差平方和模型进行计算获得参数的效果较好,否则,选用垂直残差平方和模型估算参数会更好,同时说明用该组参数进行预测效果会更好.
3 关于分布函数的取值
在分布函数的取值方面,许多学者常常忽略完整数据和截尾数据的区别[7],而将二者不区分地加以应用,这样必然会产生一定的误差,导致设备可靠性预测的不准确,管理人员错误地指导维修管理,造成设备无效的维修或维修过度.
研究发现,对威布尔分布函数取值的选取与要评估的失效数据类型有关,而试验数据和现场数据则是失效数据的两种表现类型,若将截尾数据按完整数据处理或将完整数据按截尾数据处理时均会产生差异[8],因此,通过对以下分布函数的分析来确定各值选取不同对预测结果的影响.
3.1 完整数据的估计
用平均秩估计(也称期望估计)为

式中:F为完整数据分布函数的经验取值,F值的具体选择根据所需精度而定;i为失效数据的序号;k为失效数据的个数.
用中位秩估计为

对于F的估计还有以下两式:
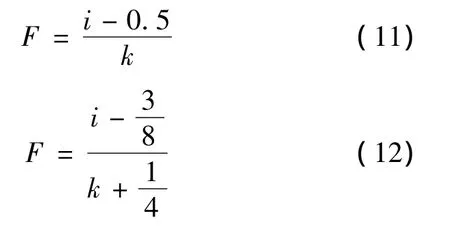
研究发现,式(9)的均方误差最大,式(12)的次之,式(11)的最小,而式(10)却是最常用的,但当k充分大时,式(9)—(12)给出的F值是非常接近的[9].
3.2 截尾数据的估计
对于截尾数据的估计,只要将式(9)—(12)中的i更换为Di=Di-1+(k+1 -Di-1)/(k+2 -j)即可进行估算,Di为第i个失效数据的序号,若令h为截尾数据的个数,k-h为失效数据的个数,以增序排列这组数据,则最小数据编号记为1,最大数据编号记为k,最小的失效数据编号记为1,最大的失效数据编号记为k-h,则j=1,2,…,k,而i=1,2,…,(k-h).

以某机械设备部件的疲劳实验采集的数据(见表1)为例说明,其中采用较常用的中位秩作为F的估计值.
从图5中可以很清楚地看到,将数据归为完整数据和归为截尾数据后所得结果具有很大不同,因此数据判断的正确性将直接影响到参数估计的精度,继而影响预测的准确度.从最小二乘法关于垂直残差最小和水平残差最小模拟的结果(见图6),可以直观地看到在此例中二者的差异是存在的,而表2的数值则更清楚地比较出两种方法的优劣性.
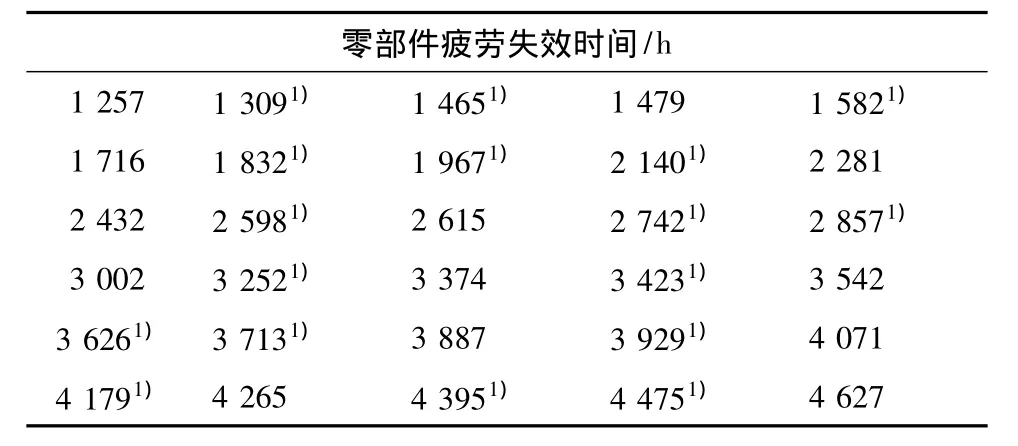
表1 设备部件的疲劳实验数据Tab.1 Fatigue test data of component of equipment
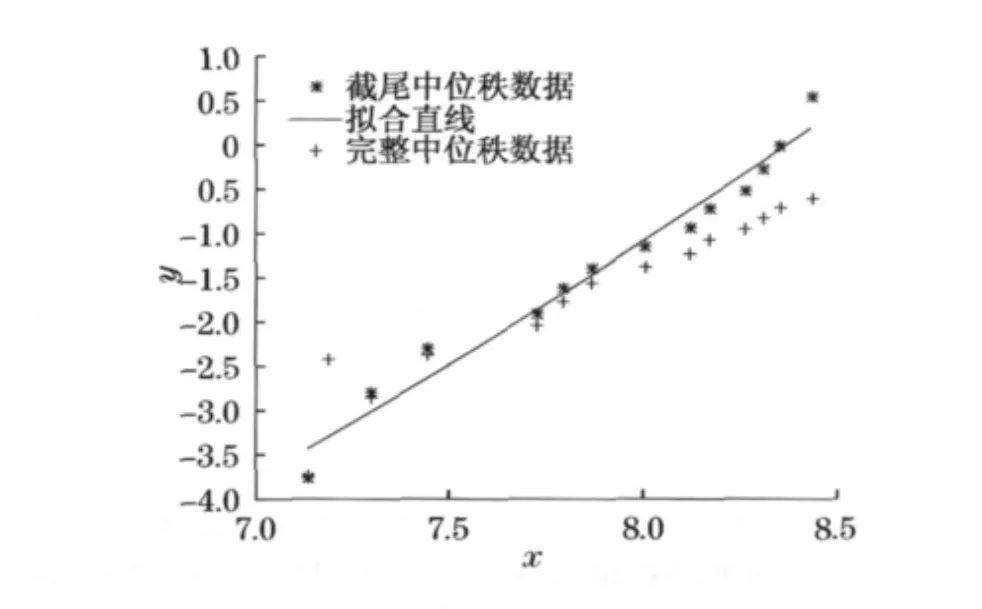
图5 完整数据和截尾数据的比较Fig.5 Comparison between completed data and censored
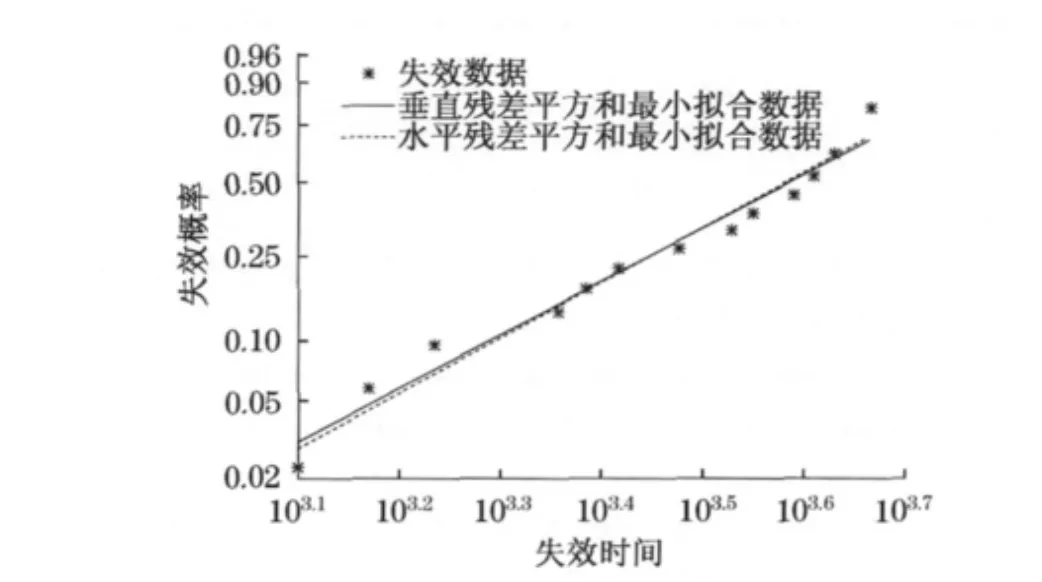
图6 垂直残差和水平残差平方和最小结果的比较Fig.6 Comparison of minimizing the sum of squares in horizontal residuals and vertical residuals

表2 两种方法的参数值比较Tab.2 Comparison of the parameter value gained from two methods above
综上可知,方法2的数据误差(Rxy=0.0613)小于方法1的数据误差(Ryx=0.4910),因此,此例中选择方法2所得到的参数值,即n=4328.1和m=2.8713,更能准确地预测该设备部件的可靠性.
4 可靠性预测
将已求得威布尔的两参数值分别代入到失效分布函数公式和可靠度函数公式中,可以得到[10]:

计算得到威布尔形状参数m=2.8713>1,则说明该部件处于“浴盆曲线”三个寿命期的耗损阶段,若估算5000h后的可靠度则将其代入到式(13)中即可,得到R(5000h)=22.02% ,由此可以预测任何时间点处的可靠性发展变化情况(如图7),根据本例估算的5000h后所得的可靠性建议采取相应措施,如需停机检修或更换机件以提高设备部件的安全性.

图7 设备部件的可靠性预测Fig.7 Reliability prediction of component of equipment
5 结论
本文基于威布尔概率图的最小二乘法展开,在应用水平残差平方和最小和垂直残差平方和最小分别对威布尔模型参数估计,以确定最佳的参数值,而在分布函数值的选取中讨论了完整数据和截尾数据对预测结果的影响,可以说,恰当的分布函数值和最小二乘法的选取能保证可靠性预测的准确性,这对延长设备的寿命,企业管理人员制定合理的维修决策具有重要的意义.
[1]刘惟信.机械可靠性设计[M].北京:清华大学出版社,1996.
LIU Weixin.The mechanical reliability design[M].Beijing:Tsinghua University Press,1996.
[2]温艳清,刘宝亮.Weibull分布在完全数据条件下的参数估计[J].山西大同大学学报,2009,25(4):17 -19.
WEN Yanqing,LIU Baoliang.The parameter estimation of Weibull distribution under the condition of completed data[J].Journal of Shanxi Datong University,2009,25(4):17 -19.
[3]方华元,胡昌华,樊红东,等.基于GA的可靠性寿命分布参数的极大似然优化估计[J].上海航天,2006(2):50-53.
FANG Huayuan,HU Changhua,FAN Hongdong,et al.The optimization estimation of maximum likelihood for reliability life distribution based on the GA[J].Shanghai Aerospace,2006(2):50-53.
[4]于晓红,张来斌,王朝晖,等.基于新的威布尔分布参数估计法的设备寿命可靠性分析[J].机械强度,2007,29(6):932-936.
YU Xiaohong,ZHANG Laibin,WANG Chaohui,et al.The reliability analysis of equipment life based on the new parameter estimation method of Weibull distribution[J].Mechanical Strength,2007,29(6):932 -936.
[5]游达章.最小二乘法在威布尔分布的可靠性评估[J].湖北工业大学学报,2009,24(4):34 -36.
YOU Dazhang.The reliability evaluation about the least square method[J].Journal of Hubei University of Technology,2009,24(4):34-36.
[6]ZHANG L F,XIE M ,TANG L C.A study of two estimation approaches for parameters of Weibull distribution based on WPP[J].Reliability Engineering and System Safety,2007,92:360-368.
[7]WU Dongfang, ZHOU Jiancheng, LI Yongdan. Unbiased estimation of Weibull parameters with the linear regression method[J].Journal of the European Ceramic Society,2006,26:1099–1105.
[8]蒋仁言.威布尔模型族[M].北京:科学出版社,1998.
JIANG Renyan. Weibull model-characteristics, parameter estimation and application[M].Beijing:Science Press,1998.
[9]SAGHAFI A,MIRHABIBI A R,YARI G H.Improved linear regression method forestimatingWeibullparameters[J].Theoretical and Applied Fracture Mechanics,2009,52:180-182.
[10]黄海,林穗华.基于威布尔分布下一个失效时刻的预测问题[J].河池学院月报,2006,26(5):30 -33.
HUANG Hai,LIN Suihua.The prediction of next failure time based on Weibull distribution[J].Monthly Report of Stream College,2006,26(5):30-33.

