橡胶浮置板轨道对城市高架箱梁减振特性数值分析

张仁巍,陈迎

(1.三明学院建筑工程学院，福建三明365004；2.广西壮族自治区交通运输厅，广西南宁530012)

橡胶浮置板轨道对城市高架箱梁减振特性数值分析

张仁巍1,陈迎2

(1.三明学院建筑工程学院，福建三明365004；2.广西壮族自治区交通运输厅，广西南宁530012)

为了研究橡胶浮置板轨道对城市高架箱梁结构的减振特性，建立了高架橡胶浮置板轨道结构三维有限元模型，分析了当减振器刚度和轨道板长度变化对高架桥系统动力响应影响。研究结果表明，减振器刚度的改变对浮置板前10阶振动频率分布影响较大，对累积质量分数分布特性几乎没有影响，相同阶数条件下浮置板的振动主频随减振器刚度减小而减小；列车通过时浮置板轨道以增大自身的振动来达到减小对桥梁结构振动能量输入的目的，在减振频率范围内，浮置板的减振效果随减振器刚度增大而减小，随浮置板长度的减小而减小。

高架轨道交通；浮置板；振动特性；有限元

高架轨道交通贯穿城市闹市区，带来的环境问题以振动噪声问题尤为突出。对于高架线路，桥梁结构的振动是结构二次辐射噪声的振源，对环境造成的影响极大[1]。钢弹簧浮置板以减少由轨道传递到高架桥结构的振动能量为目的，降低了城市高架轨道交通的振动和二次噪声水平，在国内外城市轨道交通建设中得到广泛采用。国内外学者对钢弹簧浮置板在轨道交通中减振降噪的应用方面做了大量的研究工作，主要有理论解析法、数值计算法和试验测试法等3个方面。解析理论方面，吴天行等[2-4]通过建立浮置板轨道力学模型，提出了该力学模型的动柔度求解方法，并应用数值计算分析了浮置板轨道的隔振性能及其影响因素；此外，刘学文[5]、袁俊等[6]建立了解析模型，对浮置板轨道的减振效果进行了计算分析。数值计算方面，刘维宁[7-9]、耿传智[10]、姚京川[11]、王汉民[12]和郑小康[13]等采用有限元方法分析了浮置板轨道对地铁环境振动减振特性的影响。实验测试方面，Saurenman H[14]等通过现场测试实验发现，当浮置板固有频率接近于轮对的转动频率时振动出现明显增强，Hui C K[15]、Lombaert G[16]和练松良[17]等也采用试验测试方法对浮置板轨道的减振效果进行了研究。

本文建立了高架橡胶浮置板轨道结构三维有限元模型，分析了减振器刚度变化和浮置板长度对高架箱梁结构振动响应的影响，可为城市轨道交通的减振降噪提供参考。

1 计算模型

1.1 有限元振动计算理论

使用有限元方法进行结构振动计算，可以得到在移动荷载作用下结构随时间变化的节点位移、速度和加速度的响应，基本方程为：

式中：[Me]、[Ce]和[Ke]分别为结构质量矩阵、阻尼矩阵和刚度矩阵，{üe}、{u′}和{ue}分别为结构振动加速度、速度和位移，{Fe}为荷载向量。对于上述微分方程的求解可采用Newmark等法进行求解。

1.2 计算模型及参数

桥梁结构为双线桥梁，为25 m跨混凝土简支梁结构，截面形式为单箱单室箱梁，弹性模量为3.0×1010Pa，阻尼比取0.02。钢轨类型为CHN60，采用2节点空间梁单元进行网格划分，扣件采用2节点弹簧阻尼单元进行网格划分，刚度为60 kN/mm，阻尼为7.5×103Ns/m，桥梁结构采用8节点壳单元进行网格划分，浮置板厚度为0.25 m，线间距为4.0 m，采用8节点实体单元进行网格划分，减振器的长、宽、厚为0.3m×0.45 m×0.05 m，采用8节点实体单元进行网格划分，有限元模型如图1(a）所示。在1/2梁跨断面上，分别在钢轨、浮置板、轨道中心线、翼缘、腹板和梁底设置振动拾取点，拾取列车经过时的加速度信号，拾取点分布如图1(b)所示，高架箱梁截面等效尺寸如表1所示。荷载方面，采用文献所述的车辆-轨道耦合模型计算出轨道不平顺条件下的轮轨垂向力作为有限元模型的输入荷载，车辆参数选取地铁A型车辆参数，编组形式为单节动车形式，轨道不平顺采用美国的5级不平顺谱[18]，车速为80 km/h，计算步长为5×10-4s，计算线路长度为25 m。

图1 有限元模型与拾取点分布

2 模态分析

分别改变减振器刚度，采用子空间迭代法对浮置板轨道结构和桥梁结构进行模态分析，如图2～3所示。

由图2～3可以得出以下结论：

（1）对前10阶振动而言，浮置板的振动频率受到减振器刚度影响十分明显，相同阶数条件下，浮置板的振动频率随减振器刚度的减小而减小。

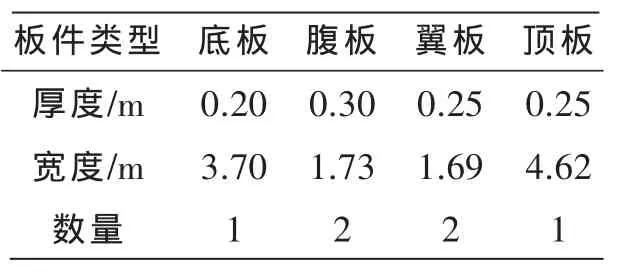
表1 高架箱梁截面板件等效尺寸

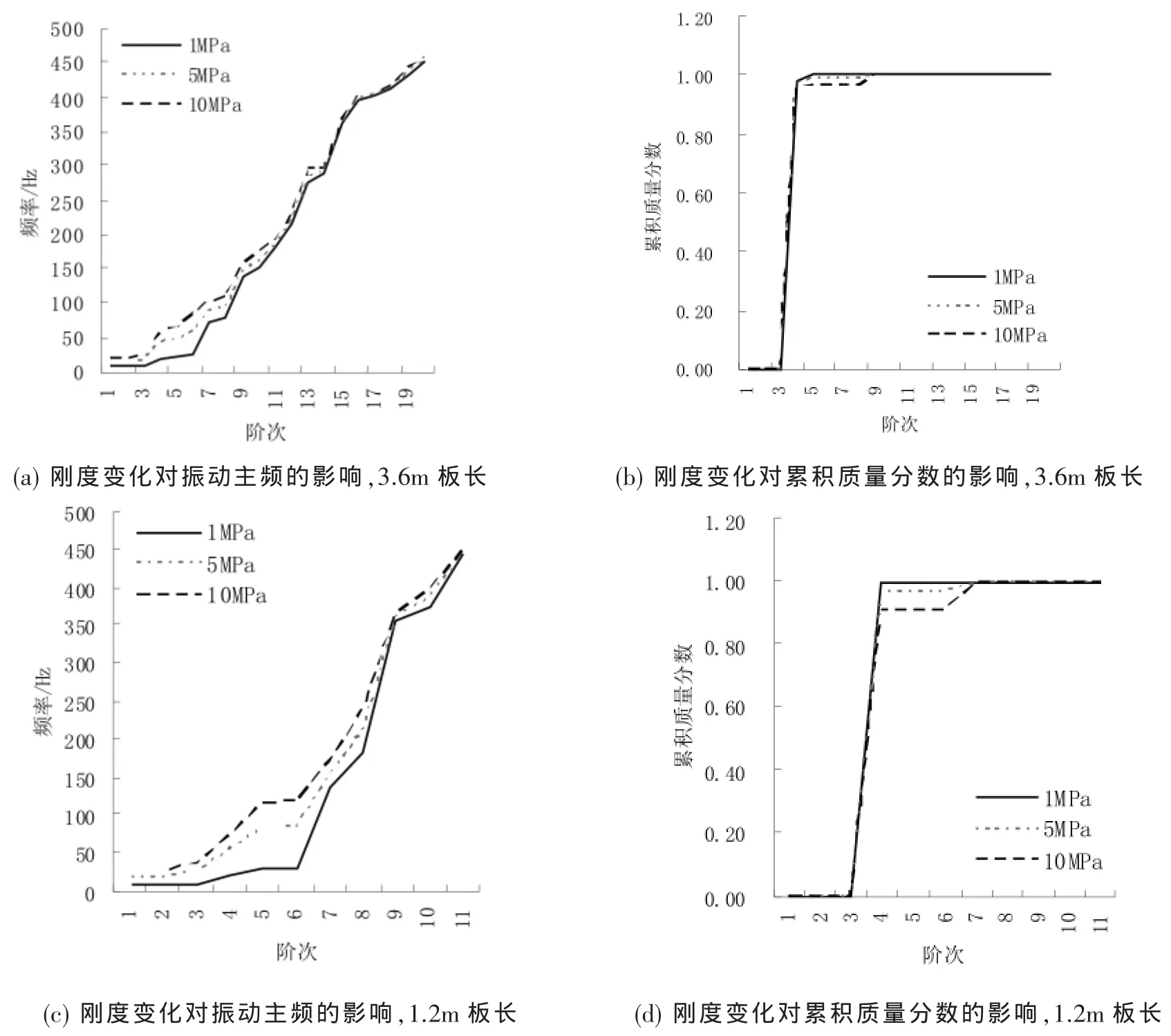
图2 减振器刚度对浮置板自振特性的影响

图3 浮置板的前10阶振型

（2)浮置板的振动累积质量分数在阶次为5时达到0.8，在阶次为10时接近于1，说明浮置板的振动能量以前10阶为主，前10阶的累积质量分数也随减振器刚度减小而略微减小。

（3)低阶振型以浮置板的平动为主,较高阶振型以浮置板弯曲和转动为主。

3 减振分析

将车辆-轨道耦合模型计算出得荷载输入有限元模型进行瞬态分析，阻尼分别为α=0.2，β=0.0002,，计算步长为10-3s，从时域和频域角度分析减振器刚度和长度变化对高架钢弹簧浮置板减振特性的影响。

3.1 时域分析

列车经过时，在减振器刚度为1.0 MPa、板长为3.6 m的条件下，各拾取点的振动加速度时程曲线如图4所示，减振器刚度和轨道板长度变化时各拾取点的振动响应幅值如表2～3所示。

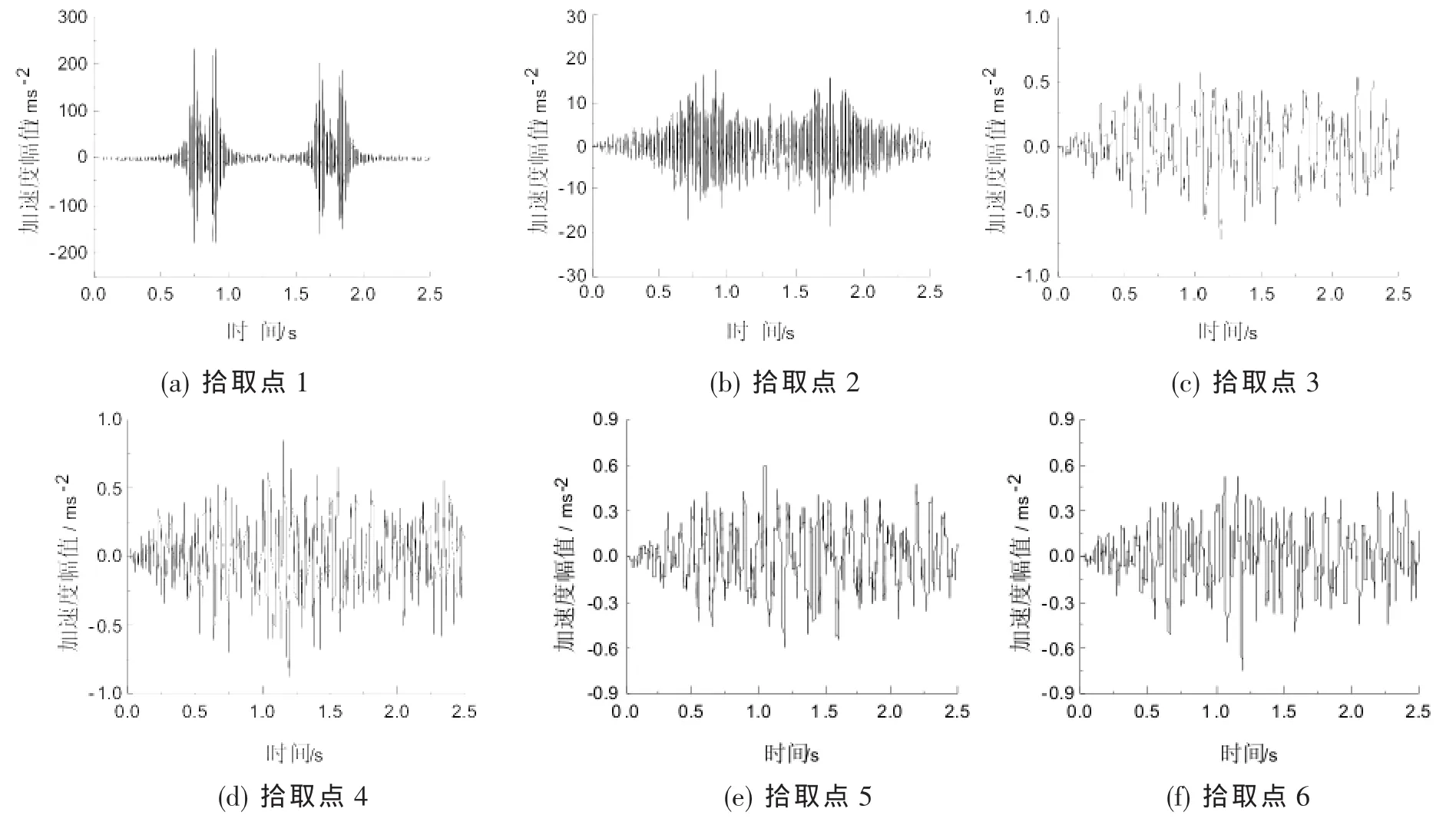
图4 各拾取点的振动加速度时程曲线

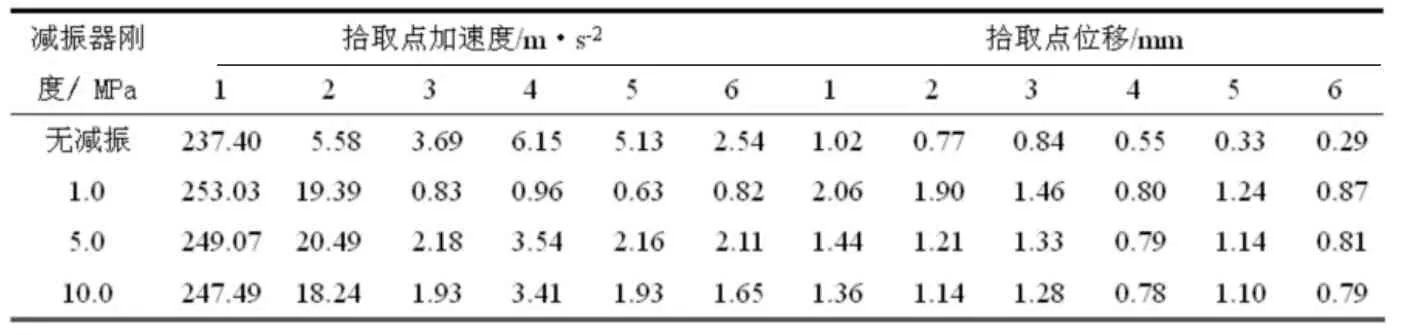
表2 3.6m板长时，减振器刚度变化对振动响应幅值的影响

表3 1.2m板长时，减振器刚度变化对振动响应幅值的影响

由图4、表2～3可以得出以下结论：

（1）列车经过时，由于轮轨的冲击作用，钢轨的加速度时程曲线峰值效应特别明显，浮置板的加速度时程曲线仍具有较明显波形起伏。对于箱梁各拾取点而言，因橡胶减振器的减振作用，桥面板、翼缘、腹板和梁底的加速度时程曲线较为平缓；

（2）浮置板顶升前，在列车荷载作用下，钢轨、浮置板、桥面板、翼缘、腹板和梁底的加速度幅值分别为236、5.59、3.70、6.20、5.15和2.58 m/s2;浮置板顶升后，钢轨和浮置板的加速度幅值分别处在225～255和17～26 m/s2范围内，桥面板、腹板和梁底的振动加速度幅值最大为4.83 m/s2。

（3）列车荷载作用下，浮置板的加速度和位移幅值随减振器刚度的增大而减小，高架桥结构各拾取点的振动加速度幅值随刚度的减小而减小，高架桥结构的位移随减振器刚度的减小而略微增大。

3.2 频域分析

对各拾取点的振动时程进行1/3倍频程分析，以分析减振器刚度变化对轨道和高架桥结构振动水平分布的影响，结果如图5～6所示。采用振动加速度级VAL对振动水平进行评价，计算方法如式(2)所示。

式中：VAL为振动加速度级,dB;arms为1/3倍频程中心频率对应的振动加速度有效值，m/s2；a0为基准加速度，取10-6m/s2。

图5 减振器刚度变化对高架箱梁振动水平的影响，板长3.6m

图5 表明，对于板长为3.6 m的浮置板而言：

（1）在小于40 Hz的频率范围内，浮置板顶升后钢轨的振动水平较顶升前高出约14.3 dB,钢轨振动水平随减振器刚度的增加而减小。

（2）在频率分析范围内，浮置板的振动水平在顶升后较顶升前高出12～23 dB，在8～40 Hz范围内，浮置板的振动水平随减振器刚度的增大而减小，在80～200 Hz范围内，减振器刚度的变化对浮置板振动水平的影响较小。

（3）在10～20 Hz范围内，浮置板顶升后箱梁各拾取点的振动水平较顶升前高出3～8 dB，在20～80 Hz范围内，当减振器刚度大于1 MPa时，箱梁各拾取点的振动水平较顶升前高出6～12 dB，在80～200 Hz范围内，箱梁各拾取点的振动水平在浮置板顶升后较顶升前发生急剧减小，减小值最大可以达45 dB，减振效果随减振器刚度的减小而增大。

图6表明，在20～50 Hz范围内，板长为1.2 m的浮置板轨道钢轨振动水平较板长为3.6 m时高出约7.8 dB；在20～100 Hz范围内，板长为1.2 m的浮置板轨道轨道板振动水平较板长为3.6 m时高出约12.8 dB；在20～200 Hz范围内，板长为1.2m时，箱梁各拾取点的振动水平较板长为3.6 m时高出4.9～6.8 dB，主要是由于浮置板长度的减小，导致相同阶次下轨道板的振动主频发生增大，进一步引起浮置板的减振效果减小。

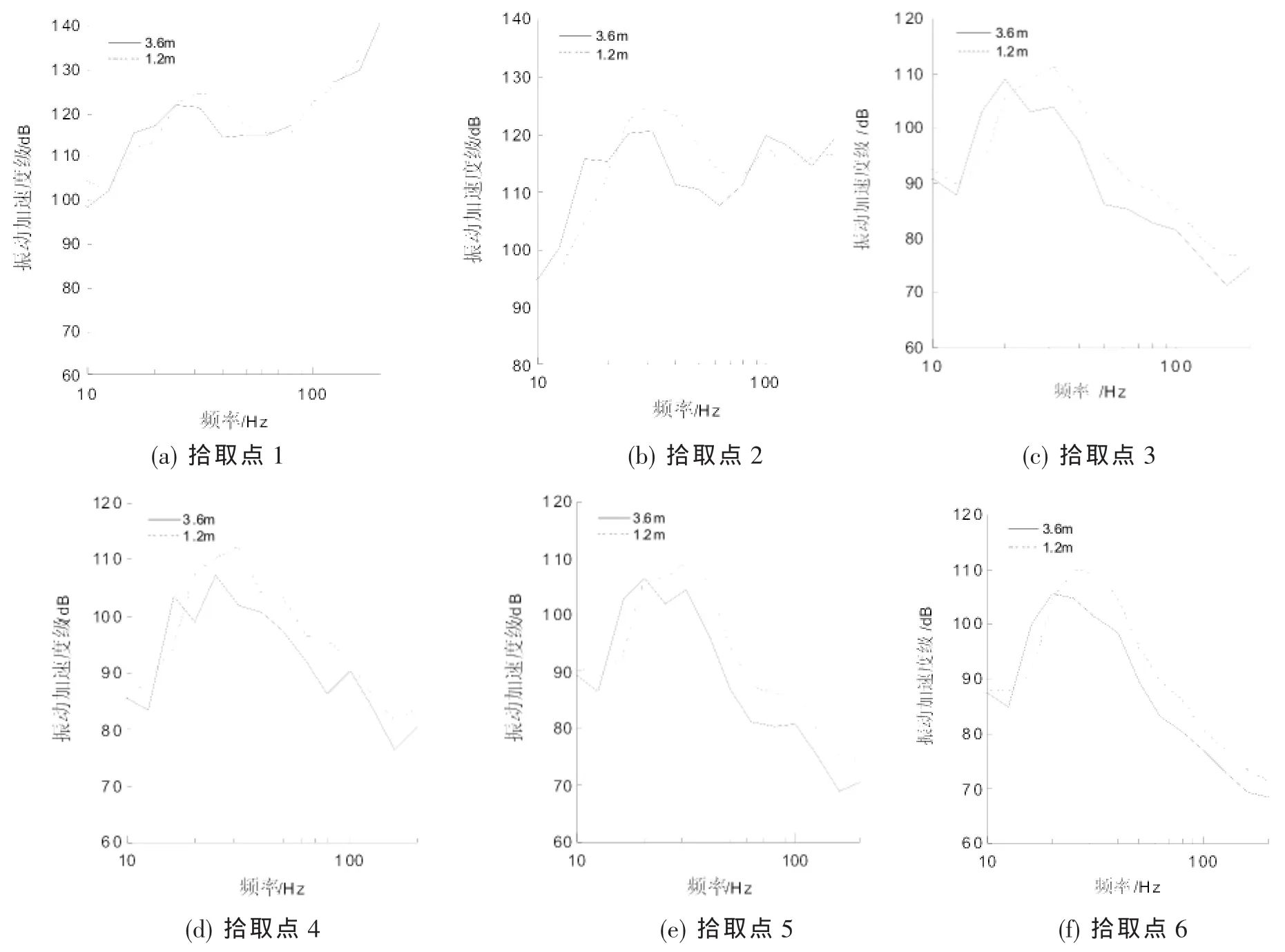
图6 浮置板板长变化对高架箱梁振动水平的影响

4 结论与建议

本文通过数值计算分析，可以得出以下结论：

(1)浮置板前10阶振动频率分布特性受到减振器刚度的影响十分明显，累积质量分数分布特性基本不受到减振器刚度变化的影响；相同阶数下，浮置板的振动主频随减振器刚度增大而增大。

(2)时域分析表明，浮置板的加速度和位移幅值随减振器刚度的减小而增大，箱梁结构的振动加速度幅值随刚度减小而减小，减振器刚度变化对箱梁结构位移的影响很小。

(3)浮置板轨道通过增大自身的振动水平从而减小了对高架桥振动能量的输入，在10～200 Hz范围内，浮置板顶升后，浮置板的振动水平较顶升前增大了约12～23 dB，箱梁结构的振动水平较顶升前的最大减小值可达45 dB，浮置板的对箱梁结构的减振效果随减振器刚度的减小而增大。

(4)浮置板长度的减小，相同阶次下轨道板的振动主频发生增大，进一步减小导致浮置板的减振效果发生。

［1］NGAI K W，NG C F.Structure-borne noise and vibration of concrete box structure and rail viaduct［J］.Journal of Sound and Vibration，2002，255（2）：281-97.

［2］李增光，吴天行.浮置板轨道二维建模及隔振性能分析［J］.铁道学报，2011，33（8）：93-98.

［3］李增光，吴天行.浮置板轨道动柔度计算方法及隔振性能研究［J］.振动工程学报，2007，20（3）：207-212.

［4］王炯，吴天行.浮置板轨道隔振性能研究［J］.上海交通大学学报，2007，41（6）：1021-1025.

［5］刘学文，吴川，谢军等.长型浮置板轨道隔振系统理论分析（Ⅰ）——弥散曲线及临界速度［J］.计算力学学报，2009，26（6）：919-913.

［6］袁俊，胡卫兵，孟昭博，等.浮置板轨道结构类型比较及其隔振性能分析［J］.振动、测试与诊断，2011，31（2）：220-228.

［7］丁德云，刘维宁，李克飞，等.钢弹簧浮置板轨道参数研究［J］.中国铁道科学，2011，32（1）：30-35.

［8］丁德云，刘维宁，张宝才，等.特殊浮置板轨道隔振效果的三维数值研究［J］.铁道学报，2009，31（6）：58-62.

［9］丁德云，刘维宁，张宝才，等.浮置板轨道的模态分析［J］.铁道学报，2008，30（2）：61-64.

［10］耿传智，楼梦麟.浮置板轨道结构系统振动模态分析［J］.同济大学学报：自然科学版，2006，34（9）：1201-1206.

［11］姚京川，杨宜谦，王澜.浮置板式轨道结构隔振效果分析［J］.振动与冲击，2005，24（6）：108-110，113.

［12］王汉民.城市轨道交通浮置板轨道振动特性研究及对邻近建筑物的影响［D］：北京：北京交通大学，2007.

［13］郑小康.地铁高架桥上浮置板轨道减振研究［D］.北京：北京交通大学，2010.

［14］SAURENMAN H，PHILLIPS J.In-service tests of the effectiveness of vibration control measures on the BART rail transit system［J］.Journal of Sound and Vibration，2006，293（3/4/5）：888-900.

［15］HUI C K，NG C F.The effects of floating slab bending resonances on the vibration isolation of rail viaduct［J］.Applied Acoustics，2009，70：830-844.

［16］LOMBAERT G，DEGRANDE G，VANHAUWERE B.The control of ground-borne vibrations from railway traffic by means of continuous floating slabs[J].Journal of Sound and Vibration，2006，297（3/4/5）：946-961.

［17］练松良，刘加华.城市轨道交通减振降噪型轨道结构的选择［J］.城市轨道交通研究，2003（3）：35-41.

［18］雷晓燕.轨道力学与工程新方法［M］.北京：中国铁道出版社，2002.

Numerical Analysis on Vibration Reduction Characteristics of Floating Slab Track in Metro Viaduct Box Girder

ZHANG Ren-wei1,CHEN Ying2
(1.College of Civil Engineering,Sanming University,Sanming 365004,China; 2.Transportation Department of Guangxi Zhuang Autonomous Region,Nanning 530012,China)

A 3D FEM model was established to analyze the vibration reduction characteristics of rubber floating slab in metro viaduct and the influence of stiffness of damper and slap length on viaduct vibration characteristics were studied.The results showed that the stiffness of damper and slap length have a large influence on the top 10 order natural frequency distribution of floating slab,and almost no effect on distribution characteristics of cumulative mass fraction,the natural frequency of floating slab track decreases as damper stiffness decreases and also the distance increases under the condition of the same order.The floating slabs reduce the vibration energy that transmits to the bridge by increasing its own vibration as trains pass.In the range of vibration reduction frequency,the vibration reduction effect of floating slab decreases with the damper stiffness decreases and increases as the slap length increases.

metro viaduct；floating slab track；vibration reduction characteristics；FEM

U211.3

A

1673-4343（2013）06-0087-07

2013-09-20

福建省教育厅科技资助项目(JA12300);福建省海西重点建设项目(HX2008-02)

张仁巍,男,江西万年人，讲师，博士研究生。研究方向：桥梁结构振动研究。