具有凸多面体不确定参数Delta算子时滞系统的可靠保性能控制
王佑恩
(三明学院信息工程学院,福建三明365004)
具有凸多面体不确定参数Delta算子时滞系统的可靠保性能控制
王佑恩
(三明学院信息工程学院,福建三明365004)
研究Delta算子描述的线性不确定时滞系统的可靠保性能控制问题。考虑系统含有具有凸多面体不确定性参数和连续模型执行器故障,根据Lyapunov稳定性理论,给出对于所有允许的不确定性和执行器故障,均使闭环系统渐近稳定且给定性能指标具有一定上界的状态反馈控制器的存在条件,由此提出相应控制器的设计方法。通过数值算例验证了设计方法的可行性。
Delta算子;可靠控制;执行器故障;时滞系统
在工程实际中,许多实际的系统都含有时滞[1-4],如化工系统、微波振荡器等。通常时滞是系统产生振荡和不稳定的根源。控制系统中存在时滞使得理论分析和工程应用增加了特殊的难度,同无时滞相比,滞后使得系统的相应性能变差,甚至稳定性难以得到保证,因而时滞系统的鲁棒控制研究也就成为研究者所关注的主要问题之一。自20世纪90年代以来,在控制理论与工程实际中,随着Matlab等系统软件分析包的广泛应用,特别是线性矩阵不等式(LMI)的引入,使得求解一些复杂的控制问题(如原来得出的稳定性条件是一个黎卡提代数方程)非常困难,而通过线性矩阵不等式的鲁棒稳定性条件,提出用线性矩阵不等式求解控制问题,使得算法更加简化[5-6],进行了广泛的研究。肖乐等利用Lyapunov泛函方法讨论了不确定线性时滞系统的相关状态反馈鲁棒镇定问题[1];钱伟、马维军等研究线性时滞系统输出动态反馈镇定问题[3-4];罗跃生等研究了状态具有多个时滞的线性系统的保成本容错控制等[2]。
目前,在控制理论研究者,存在连续系统和离散系统两大研究领域。一般说来,离散时间系统的研究结论较适用于计算机实线,连续系统的研究结论便于理论研究。而两大系统的结论表面看起来有很大的不同,一般很难找出其中的联系。Delta算子理论则是联系二者的桥梁。Delta算子理论于20世纪80年代即被控制界提出,并进行了广泛的研究[6-8]。如肖民卿针对传感器故障的Delta算子不确定系统的鲁棒稳定性控制等[6]。
本文针对一类Delta算子描述的凸多面体参数不确定时滞系统,研究采用状态反馈来实现系统的鲁棒可靠保性能控制问题。运用Lyapunov稳定性理论和LMI方法,给出满足性能指标要求的状态反馈控制器的存在条件和设计方法。
1 问题描述
对于一类由Delta算子描述的不确定时滞系统
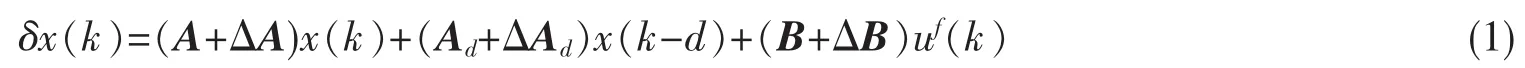
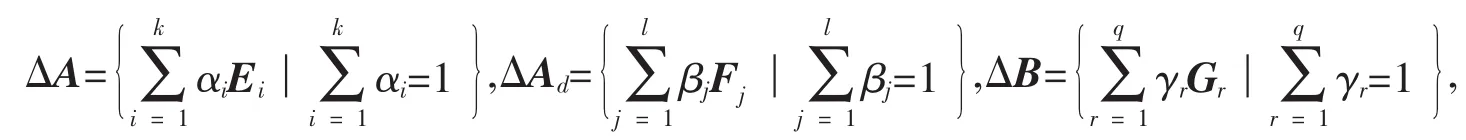
其中Ei∈Rn×n(i=1,2,…,k),Fj∈Rn×n(j=1,2,…,l),Gr∈Rn×p(r=1,2,…,q)是已知实矩阵,αi≥0(i=1,2,…,k),βj≥0(j=1,2,…,l)和γr≥0(r=1,2,…,q)是未知的有界标量。
Delta算子系统(1)的性能指标定义为:

其中Q、R是给定的对称正定的加权矩阵.考虑状态反馈控制器

由于执行器可能存在故障,因此设被控对象的实际输入信号模型为:

其中M=diag{m1,m2,…,mp}为执行器故障矩阵,且mi(=1,2,…,p)满足0≤mli≤mi≤mui,这里mli,mui为已知正常数且满足0≤mli≤1≤mui。
为方便起见,记:
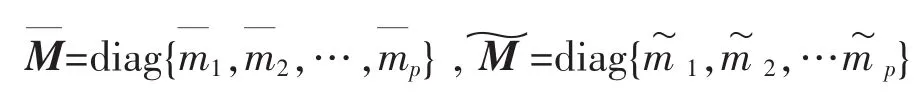
这样,将(4)式代入(1)中,得到Delta算子时滞闭环系统:

本文所研究的问题是:对于含执行器故障系统的Delta算子时滞系统(1),寻找一个状态反馈控制律K,使得对所有容许的不确定矩阵F和所有可能的执行器故障矩阵M,闭环系统(5)是渐近稳定的,并且性能指标J满足J≤J*,J*是某个常数。
2 主要结果
在这部分,将给出一个闭环系统(5)渐近稳定的充分条件,然后提出一个方案设计控制器。首先介绍两个个引理:
引理1[6]给定适维矩阵Y、C和D,其中Y是对称的,如果存在对角矩阵U>0,使得

那么对所有满足的对角矩阵,都有Y+CHDT+DHCT<0。
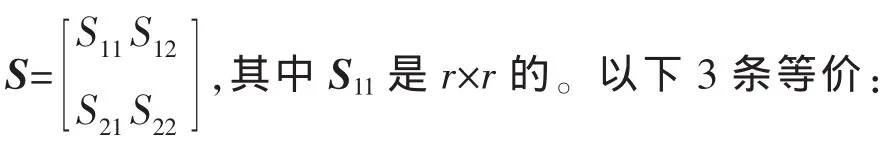
①S<0,
②S11<0,S22-S12TS11-1S12<0,
③S22<0,S11-S12S22-1S12T<0。
定理1给出不确定Delta算子系统(1)存在保性能控制的充分条件。
定理1对于Delta算子时滞系统(1),如果存在矩阵K,对称正定矩阵P,S,使得对所有的不确定性F和所有可能的执行器故障矩阵M,矩阵不等式

成立,其中Φ1=h-1(h+I)TP(h+I)-h-1P+S+Q+KTMRMK,Φ2=(h+I)TPd,Φ3=hdTPd-S,则u(k)=Kx(k)是δ算子时滞系统(1)的一个可靠保性能状态反馈控制器,且性能指标满足

这里x(-i),i=1,2,…,d*为系统的初始状态。
证明若定理条件成立,记Φ¯1=h-1(hA¯+I)TP(hA¯+I)-h-1P+S,则有


由x(k+1)=hδx(k)+x(k),代入上式整理得:
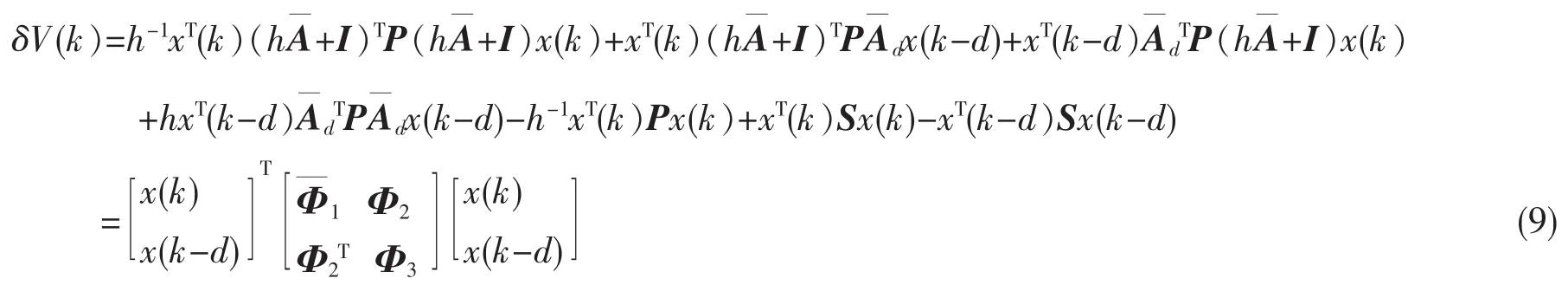
由(8)式,可得
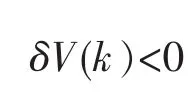
从而,由δ域Lyapunov稳定性理论,闭环系统(5)是渐近稳定的.又由(6)式和(9)式,可得
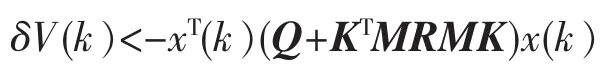
即
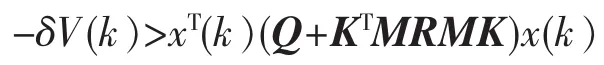
上式两边对从k到∞求和,并利用系统的稳定性可得:

定理得证。
以下定理给出了不确定Delta算子系统(1)的保性能可靠控制律存在条件,并提出了保性能控制律的构造方法。
定理2对于Delta算子时滞系统(1),如果存在矩阵W,对称正定矩阵X,N,以及正定对角矩阵U,使得


证明由定理1,如果存在矩阵K,对称正定矩阵P,S,使得(6)式成立,则是Delta算子时滞系统(1)的一个可靠保性能状态反馈控制器。令


将不确定性ΔA,ΔAd,ΔB代入上式整理得:

注意到(11)式给出的闭环系统性能上界依赖于系统的初始条件,为了避免这种依赖,我们采用这样的处理方法:假定系统的初始状态是未知的,但均属于集合

其中Z是一个已知常数矩阵.从而,由(11)式可得
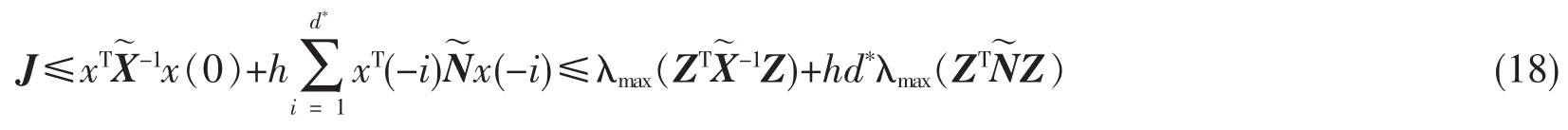
定理2提供了不确定Delta算子时滞系统(1)的鲁棒可靠保性能控制器的一种设计方法。不等式(10)是关于变量ε,X,W,N的一个线性矩阵不等式,因此可以应用LMI工具箱中的求解器feasp来判断该线性矩阵不等式的可行性问题。如果这个线性矩阵不等式是可行的,该求解器会提供一个可行解那么令K=,状态反馈控制器u(k)=Kx(k)就是系统(1)的一个可靠保性能控制器,且闭环系统的性能指标满足(18)式。
进一步地,可以通过建立和求解以下最优化问题来使性能指标的上界尽可能的小,从而得到一个“最优”(准确的说,应该是“较优”)的可靠保性能控制器。

3 数值算例
考虑Delta算子时滞系统(1),其中

采样周期h=0.1,状态时滞上界d*=5。假定系统执行器故障模型如(5),其中

系统性能指标如(3),其中加权矩阵
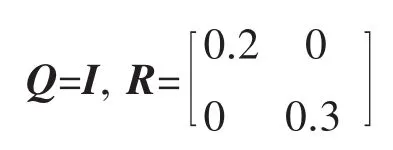
设初始状态集(17)中,Z=1.5I。
根据上文提出的设计方法,应用MATLAB的LMI工具箱中求解器feasp求解线性矩阵不等式(10),得到可行解为
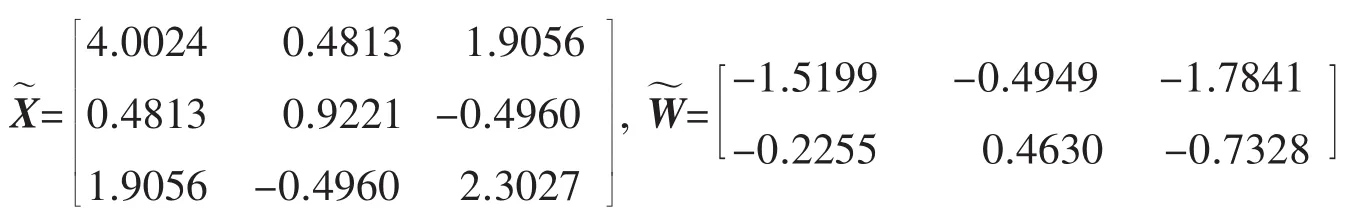
表明Delta算子时滞系统(1)存在可靠鲁棒保性能状态反馈控制器,控制律为

此时闭环系统的性能指标J的上界J=10.0193。
进一步地,考虑“最优”可靠鲁棒保性能控制器设计问题。应用MATLAB的LMI工具箱中求解器mincx求解相应的最优化问题(19),结果显示最优解如下:
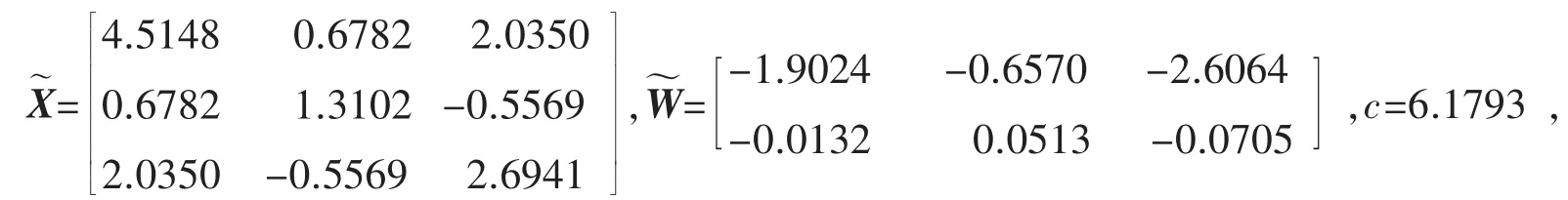
利用最优解求出Delta算子时滞系统(1)的“最优”可靠鲁棒保性能状态反馈控制律为

闭环性能指标上界J的上界c=6.1793。
4 结束语
本文针对一类Delta算子描述的凸多面体参数不确定时滞系统,研究采用状态反馈来实现系统的鲁棒可靠保性能控制问题.运用Lyapunov稳定性理论和LMI方法,给出满足性能指标要求的状态反馈控制器的存在条件和设计方法。
[1]肖乐,伞治,朱弈.不确定线性时滞系统时滞相关状态反馈鲁棒镇定[J].系统工程与技术,2013,35(4):802-806.
[2]罗跃生,龚新平,李彤.连续多时滞系统的保成本容错控制[J].系统工程与技术,2012,34(5):1012-1017.
[3]钱伟,沈国江,孙优贤.基于LMI的线性时滞系统输出动态反馈镇定[J].控制与决策,2008,23(5):546-550.
[4]马维军,朱寰,宇张显.线性离散时滞系统的输出反馈镇定[J].电机与控制学报,2013,17(1):88-93.
[5]赵岩峰,陈东彦,胡军.凸多面体不确定线性时滞系统鲁棒稳定性条件[J].哈尔滨理工大学学报,2009,4(14):127-130.
[6]肖民卿.传感器有故障的Delta算子线性不确定系统的鲁棒D-稳定[J].控制理论与应用,2009,26(2):183-185.
[7]胡军,陈东彦,赵岩峰.改进的凸多面体不确定离散线性系统的鲁棒稳定条件[J].哈尔滨理工大学学报,2010,15(2):99-101.
[8]GOODWIN G C,MIDDLENTON R H.Ropprochement between continuous and discrete model reference adoptive control[J].Automotica,1986,22(6):199-207.
[9]苏宏业,褚健.不确定时滞系统的鲁棒控制理论[M].北京:科学出版社,2007.
[10]毛影岩,任雪芳,余晃晶.动态知识表达系统的鲁棒性[J].三明学院学报,2008,25(4):379-382.
Reliable Guaranteed Cost Control for Delta Operator Systems with Time-delay and Parameter Uncertainties of Convex Polyhedron
WANG You-en
(School of Information Technology,Sanming University,Sanming 365004,China)
The problem of reliable guaranteed cost control for a class of delta operator formulated systems with time-delay and parameter uncertainties is studied in this paper.Convex polyhedron uncertainties and actuator failures with continuous model are considered.Based on Lyapunov theory in delta domain,a sufficient condition of existence of the controllers is presented in terms of linear matrix inequalities,which makes the close-loop systems robust asymptotically stable and the value of cost function less than a certain upper bound for all admissible uncertainties and actuator failures.And then a design method of the controllers is proposed.A numerical example is given to illustrate the availability and effectiveness of the method.
delta operator system;reliable control;actuator failures;time-delay system
TP273
A
1673-4343(2013)06-0009-08
2013-09-17
三明学院科研基金项目(B201206/Q)
王佑恩,男,福建三明人,助教。研究方向:Delta算子系统研究。

