有限元技术优化客车转向支架受扭强度分析

蔡建进，邵明亮

（厦门理工学院机械与汽车工程学院，福建厦门361024）

有限元技术优化客车转向支架受扭强度分析

蔡建进，邵明亮

（厦门理工学院机械与汽车工程学院，福建厦门361024）

转向支架在客车行驶时的安全性起着举足轻重的作用。转向支架经过有限元技术分析优化后，安装在客车底盘上，在加载1.5 t和加载4.5 t两种工况下进行测试。转向盘分别逆时针左转再顺时针右转，在不同的转角下采集处理转向支架受扭的应变应力。测试结果表明，该客车转向支架强度符合设计要求，同时测试数据为研究转向支架的受力情况提供了有价值的信息。

转向支架；有限元技术；转角；应变

转向支架作为客车联接转向轮和转向盘的重要部件，对客车的安全性起着举足轻重的作用。采用ANSYS有限元软件对其结构建模，找到了整个结构刚度的薄弱环节［1］,并利用有限元技术对其进行强度仿真分析，找出了产生裂纹破坏的位置，结合有限元分析结果对其利用结构优化技术进行优化研究［2-3］。但优化后的支架是否能满足力学性能要求，需要进行试验验证。本文测试是在客车底盘上进行，客车还没安装车身。通过在转向支架上粘贴应变片，再把转向支架装入客车底盘。转动转向盘加载，测试分析转向支架的受扭强度。

1 客车转向支架受扭测试试验

转向支架下端分别与左、右转向横拉杆相连，上端与转向盘相连。根据实际情况可知：对转向支架安装方孔进行全约束［4］。在客车底盘上分别加载1.5 t和4.5 t,当客车转动转向盘时，转向支架主要受到扭曲变形。采用ZL-1L型转向参数测试仪测量转角，CM-1J-32型数字静态应变仪测量应变。

1.1 测点的选择与布片方案

在转向支架粘贴应变片，它的工作原理是：把所使用的应变片按构件的受力情况，合理地粘贴在被测构件变形的位置上，当构件受力产生变形时，应变片也随之变形，电阻值就发生相应的变化，其变化量的大小与构件变形成一定的比例关系，通过测量电路得到受力后的应力、应变值或其它的物理量［5］。沿受扭方向，在箱形结构的边角，沿棱线方向中点选择4个测试点，每点沿与棱线45°和-45°各粘贴一应变片。粘贴位置如图1所示，图2为粘贴好应变片的转向支架。

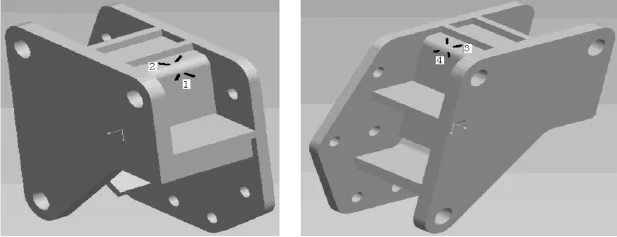
图1 测点1，2，3，4位置

1.2 转向支架受力分析

当轴受扭时，其表层各点均处于纯剪切状态，根据切应力互等定理，在两个互相垂直的两个平面上，剪应力必然成对存在，且数值相等，两者都垂直于两平面的交线，方向则共同指向或共同背离这一交线［6］。即主应力σ1与σ3与轴线分别成-45°与45°，见图3。而且

图2 粘贴应变片的转向支架

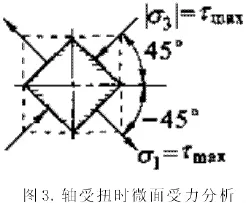
图3 轴受扭时微面受力分析

根据胡克定律，沿主应力σ1方向的正应变为

从公式（2）可知，从应变仪上读出或记录出应变的大小，即可计算出应力值。

1.3 测试电桥

测试应变片采用一对90°的应变片，沿主应力σ1方向沿轴线成45°和135°粘贴应变片R1和R2，每对应变片分别组成半桥，这样就有4个测点。如图4所示［7］。

电桥桥臂系数计算如式（3）：

应变片真实值：

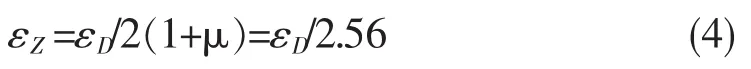
其中：n为桥臂系数；μ为泊松比，取0.285；εD为读数应变值；εZ为真实应变值

应力真实值：

其中E为弹性模量，E=2.1×106 kg/cm2=210 GPa。

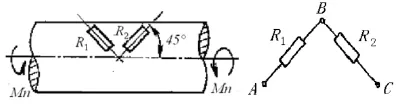
图4 半桥测量扭矩布片与接桥

2 测试结果分析

转向支架测试在两个工况下进行：第一次加载1.5 t，转向盘逆时针左转再顺时针右转；第二次加载4.5 t，转向盘逆时针左转再顺时针右转。车轮附着路况为较光滑的水泥路面。当转向轮在正中间时，转角为零；左边转角为正，右边转角为负。每次转角大约为20°，直到转向盘转动一周。记录下每次转角对应的四个测点应变读数值εD（με）。

2.1 工况1：加载1.5 t

给客车底盘加载1.5 t，转向盘从中间零度开始逆时针左转，转动一周，即360°。依次采集了每次转角对应4个测点的应变数据，作“转角-应变”关系曲线图，见图5所示。

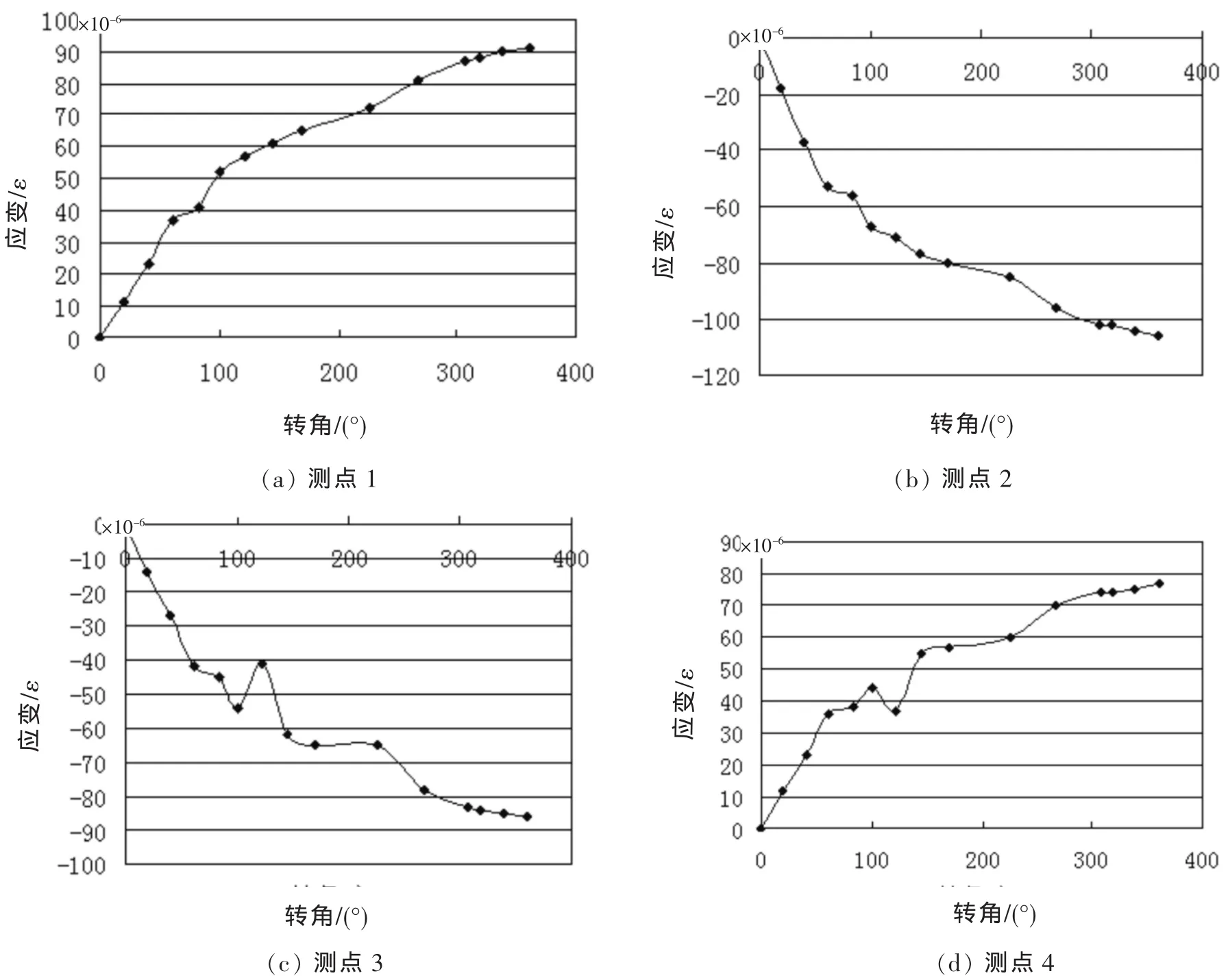
图5 加载1.5 t时逆时针左转“应变-转角”关系曲线

实验共采集了十几次数据，当转向盘从中间零度开始时，转向支架受扭曲变形为0。它的应变随着转向盘转角的增加而逐渐增大。测点3和测点4在转角大概120°应变出现了一些波动，这可能和它们的位置及地面粗糙度有关。另外，测点1和测点4受到的应变值为正，表明它们受到的是拉应力；而测点2和测点3受到的应变值为负，表明它们受到的是压应力，符合转向支架的受力情况。

当转向盘逆时针左转到360°后，开始顺时针右转，转到0°再顺时针右转360°。记录下每次转角对应的4个测点的应变数据。作“转角-应变”关系曲线图，见图6所示。

图6 加载1.5 t时，顺时针右转“应变-转角”关系曲线

在测试中，当转向盘逆时针左转后开始顺时针右转时，转向支架4个测点的应变发生了急剧的变化，应变值迅速的减小。原来转向支架受到转向轮和转向盘共同作用，变形越来越大，但现在转向盘对它的作用力突然减少了，自然应变值也减少了。同时4个测点的受力也发生了一些变化，和逆时针左转工况正好相反，测点1和测点4受压应力，测点2和测点3受拉应力。当转向盘顺时针右转至0度附近时，此时转向支架4个测点的应变都出现了一些波动，但都没有回到0，这是因为它们还受到一定的残余应力的影响。

由于采集的“转角-应变”数据众多，应变较大值都出现在转角较大的时候。取5次高应力区数据计算值作分析。经公式（4）计算各个测点的真实应变值εZ，经公式（5）计算出真实应力σ。转向盘逆时针左转较大应力计算见表1，顺时针右转较大应力计算见表2。

根据表1～2，可以发现，转向支架在1.5 t载荷作用下，它的受力应变具有以下的特点：

（1）受力情况：逆时针左转工况，测点1和测点4受拉应力，测点2和测点3受压应力，反向时（顺时针右转工况），正好相反。符合转向支架的受力情况。

（2）应力大小：逆时针左转工况还是顺时针右转工况，测点2的应力最大，逆时针左转工况真实应力达-87 kg/cm2，顺时针右转工况真实应力达123 kg/cm2。

（3）测点1和测点4，逆时针左转工况和顺时针右转工况的应变值大小差不多。两个工况比较，测点1之间最大应力相差3 kg/cm2；测点4之间最大应力和均值均相差1 kg/cm2。

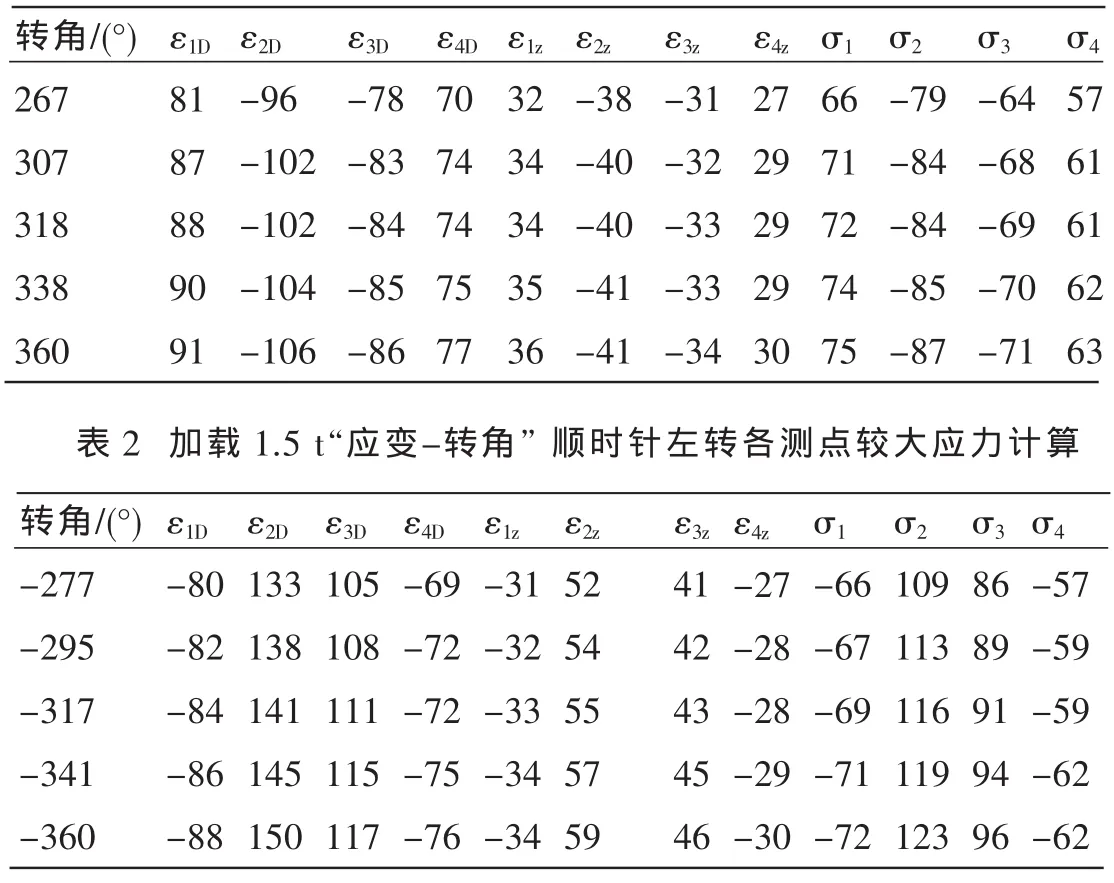
表1 加载1.5 t“应变-转角”逆时针左转各测点较大应力计算

（4）测点2和测点3，顺时针右转工况均大于逆时针左转工况。其中测点2之间最大应力相差36 kg/cm2；测点3之间最大应力相差25 kg/cm2。

（5）转角越大，应力越大。最大应力值区域出现在转向盘转到极大位置时段。

2.2 工况2：加载4.5 t

在客车底盘上加载4.5 t，转向盘转至中间位置，数字静态应变仪和转向参数测试仪分别调零。转向盘从中间零度开始逆时针左转，转动一周，即360°。依次采集了每次转角对应4个测点的应变数据，作“应变-转角”关系曲线图，见图7所示。

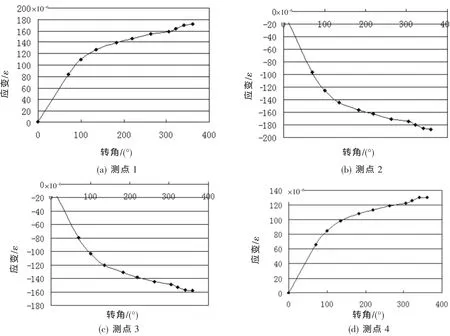
图7 加载4.5 t时，逆时针左转“应变-转角”关系曲线

加载4.5 t时，4个测点的受力方向和加载1.5 t时一样，即测点1和测点4受到的是拉应力；而测点2和测点3受到的是压应力，随着转向盘转角的增大，转向支架的应变变化更加明显。4个测点的应变值都比加载1.5 t时要大。

同样地，当转向盘逆时针左转到360°后，开始顺时针右转，转到0°再顺时针右转360°。记录下每次转角对应的4个测点的应变数据。作“转角-应变”关系曲线图，见图8所示。

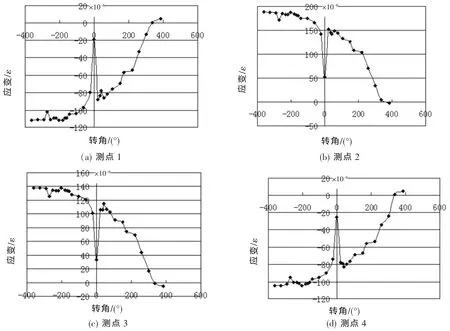
图8 加载4.5 t时，顺时针右转“应变-转角”关系曲线

和加载1.5 t一样，当转向盘逆时针左转后开始顺时针右转时，转向支架4个测点的应变发生了急剧的变化，应变值迅速的减小。测点1和测点4受拉应力很快转换成压应力，测点2和测点3受压应力很快转换成拉应力。当转向盘顺时针右转至0°附近时，此时转向支架4个测点的应变出现了突变，这比加载1.5 t明显，应力值在0°变小，但都没有回到零。

取5次高应力区数据计算值作分析。分别计算出各个测点的真实应变值εZ和真实应力σ。转向盘逆时针左转较大应力计算见表3，顺时针右转较大应力计算见表4。

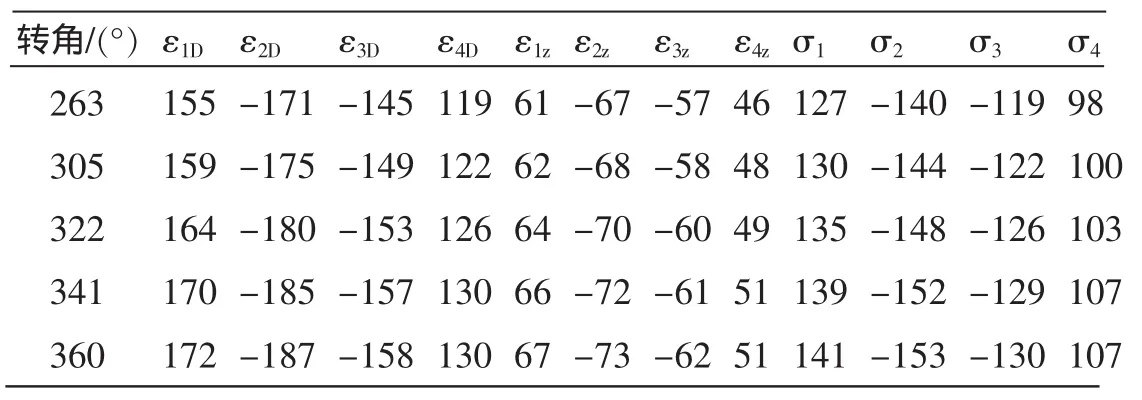
表3 加载4.5 t“应变-转角”逆时针左转各测点较大应力计算

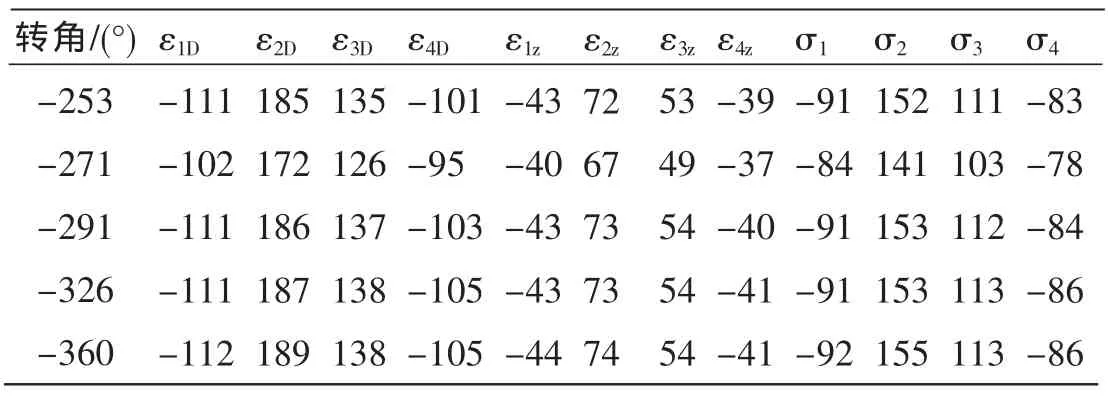
表4 加载4.5 t“应变-转角”顺时针左转各测点较大应力计算

根据表3～4，可以发现，转向支架在4.5 t载荷作用下，它的受力应变具有以下的特点：

（1）4个测点的受力方向和加载1.5 t一样，转向盘顺时针右转时，都发生了同样的变化。

（2）测点1在顺时针右转工况比在逆时针左转工况的应变值明显减少了，这比加载1.5 t要明显，在4个测点中，它相差最大，最大应力相差49 kg/cm2；其次为测点4和测点3，测点2相差最小。

（3）最大值出现在测点2，数值接近，两种工况间最大值仅差2 kg/cm2。

（4）测点1、测点3和测点4，逆时针左转工况的受力均大于顺时针右转工况。

（5）总体来看，转角越大，应力越大。最大应力值区域出现在转向盘转到极大位置时段。

3 结论

在1.5 t和4.5 t这两种不同载荷的作用下，经过有限元技术分析优化后的转向支架采集处理的数据符合它的受力情况。但转角和应变关系发生了一些变化。比较这些测试数据，可以得出以下结论：

（1）4个测点在两种工况下，应力的变化趋势是随转向盘向左、向右转动而增加，最大应力值区域都出现在转向盘转到极大位置时段。

（2）两个工况最大值都出现在测点2位置（位置在零件的右上，见布片图）。它的应力值都小于材料的屈服极限。

（3）从总的受力变化情况看，加载1.5 t时，顺时针右转工况大于逆时针左转工况。而加载4.5 t时，逆时针左转工况的受力大于顺时针右转工况。

（4）在4.5 t载荷作用下，转向支架4个测点受到的应力都比加载1.5 t大，在转向盘转到0°，曲线突变比较明显。

（5）在4.5 t载荷作用下,测点1在转向盘逆时针左转和顺时针右转的应变变化比加载1.5 t大；而测点2则相反。

测试是在客车还没安装车身的时候进行，按照客车实际承受载荷进行加载。测试的应力值都小于材料的屈服极限。表明该客车优化后的转向支架符合设计的要求。同时，测试的结果为了解转向支架的受力情况提供了有价值的信息。

[1]陈庆堂．基于ANSYS的数控铣床整机结构有限元分析［J］．三明学院学报，2010，27（2）:144-147．

[2]黄庆，杜登惠，黄小飞．动力总成悬置支架的多工况拓扑优化［J］．汽车技术，2008(10)：27-30．

[3]林涛，闫剑韬，吕兆平．基于CAE分析变速器后悬置支架优化设计［J］．装备制造技术，2010(10)：53－55．

[4]张仁斌,黄义勇,成全胜.基于ABAQUS的某微型车辆转向支架优化分析［J］.机械设计与制造,2012（7）:191-193.

[5]熊诗波，黄长艺.机械工程测试技术基础[M].北京:机械工业出版社，2011.

[6]范钦珊，殷雅俊.材料力学[M]．北京:清华大学出版社，2004.

[7]邵明亮，李文望．机械工程测试技术[M]．北京:电子工业出版社，2010.

The Analysis on Bus'Steering Bracket Turning to Torsion Strength by Optimized of Finite Element Technology

CAI Jian-jin，SHAO Ming-liang
(School of Mechanical and Automotive Engineering,Xiamen University of Technology,Xiamen 361024,China)

Steering bracket plays a very important role in the bus driving safety.The steering bracket is optimized through the analysis of finite element technology and then it is tested in loading 1.5t and loading 4.5 t for two kinds of working conditions.Steering wheel counterclockwise turn left and clockwise turn right respectively,in different angle the torsioning strain stress of steering bracket is collected and processed.Test results show that the strength of bus'steering bracket complies with the design requirements,which provide valuable information for the study of steering bracket stress.

steering bracket;finite element technology;angle;strain

U463.4

A

1673-4343（2013）04-0056-07

2013-05-13

国家自然科学基金项目（61104225）

蔡建进，男，福建厦门人，实验师。研究方向：机械设备检测与诊断。