基于多人博弈的无线传感器网络簇内信息融合算法
陈亦萍
(福州大学至诚学院计算机工程系,福建福州350002)
基于多人博弈的无线传感器网络簇内信息融合算法
陈亦萍
(福州大学至诚学院计算机工程系,福建福州350002)
利用多人博弈的思想对簇内节点间协作和竞争的关系进行分析,提出一种簇内信息融合算法。通过仿真实验对节点能量消耗的均衡性、网络生存周期及信息融合精度等方面进行性能评估验证该算法的有效性。
无线传感器网络;数据融合;博弈论
无线传感器网络(wireless sensor networks,WSN)[1]为了获取更加精确的感知信息,通常在监测区域内部署高密集性的传感器节点。如此大规模的部署导致大量冗余节点的存在,使得系统具有很强的容错性同时大量节点能够增大覆盖的监测区域减少盲区的存在。但是从通信能量角度而言,冗余节点的存在会消耗网络资源,造成能源的浪费。密集性的节点部署导致同簇内相邻近节点对同一监测对象的感知信息中具有高度的相关性和冗余性。考虑到无线传感器网络受能量有限、带宽受限等问题困扰,大量冗余节点的数据传输将会消耗大量的通信能量,并容易造成网络的拥塞,浪费通信带宽。因此对于能源受限制的无线传感器网络而言,通过研究更加合理有效的冗余节点处理机制和数据融合技术,减少网络能源浪费对于延长网络的生命周期有重要的意义[2-3]。
论文借鉴了博弈理论[4]对节点这种协作与冗余的关系进行分析,提出一种簇内基于多人博弈的信息融合优化算法(an optimized algorithm of data fusion based on multi-players game theory,DFEAMG)。在保证网络的覆盖度、可用性及监测信息精确度的前提下,DFEAMG有效地对簇内节点进行融合处理,减少了网络中冗余、无效的数据传输,达到簇内节点能量消耗的优化。
1 问题描述
在无线传感器网络分簇拓扑结构中,假设存在n个同质的传感器被划分为K个分簇结构分布在某一区域范围内,它们彼此独立对同一对象的同一属性进行观测,一个簇结构构成一个局部的融合系统。若某个簇结构有m个成员节点,对于第i成员节点,令Si表示其的传输策略,具体定义如公式(1),同时令Zi表示其在某一时刻的观测值。为了简化问题,簇首节点按公式(2)对收集到的数据采用均值融合。

同时,由节点能量消耗分析[1]可知,节点无线通信模块消耗绝大部分能量并且当处在发送状态时能量消耗最大。可以通过减少簇内处在发送状态的节点有效地对进行能量优化。同时节点间通过协作提高融合结果的精确度、保证系统的容错性,因此如何在保证不影响融合结果精确度的情况下,获得簇内能耗优化的传输方案是该算法研究的目标。
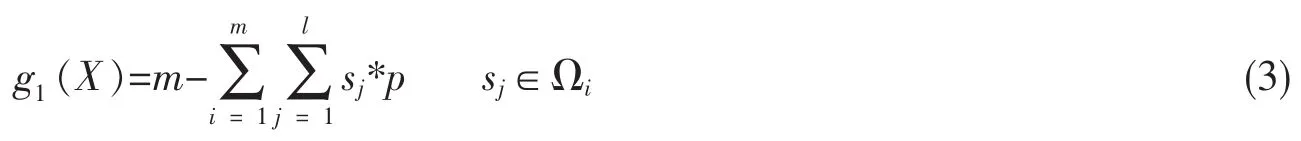
g1(X)代表簇内能量消耗量,其中Ωi是si的簇内邻居节点的传输策略集,X表示局部融合系统内传输策略,p为惩罚常数。每个采样周期中,对于同一监测目标进行感知的簇内邻居节点获得的感知数据具有高度的相似性和冗余性。因此通过引入一个惩罚常数来调整簇内邻居节点传输策略,减少冗余节点传输数据。
为了保证簇内均值融合结果的精确度,在簇首节点收集到的数据必须满足最小偏差。这样可以同时用于调整簇内邻居节点的传输策略,防止过少的节点传输数据导致最后影响最后融合结果。g2(X)表示融合结果精确度,其中Zk表示按X传输策略传输获得到数据集合。std为求标准偏差函数。

参与主体的效益函数定义式(5):

w1、w2分别表示g1(x)和g2(x)的权重,代表算法中能量消耗和融合结果精确度之间的均衡关系,用于调整簇内节点的传输策略。
2 DFEAMG算法
2.1 算法思想
簇内多人博弈信息融合优化算法(DFEAMG)通过对簇内节点关系进行分析,节点间的冗余和协作关系构成了博弈模型中的竞争和合作关系。算法试图通过在簇内成员节点间以自适应方式寻求一种传输组合方式,对簇内节点消耗能量进行优化并保证融合结果的精确度。将簇内成员节点相互竞争映射为多人博弈[5-7],如何通过非合作博弈获取最优的收益的过程视为多人博弈的优化过程即从非均衡状态向均衡状态的动态调整过程。在初始节点根据自身的剩余能量随机做出决策,依赖于各节点最优反映动态的学习思想,在重复博弈的过程中获得个主体合理的决策分配从而实现融合结果的最优化。
2.2 博弈结构
DFEAMG模型将融合系统与博弈过程进行了映射,能够体现出簇内冗余环境中各节点策略选择的过程。该博弈结构可以定义为:

其中,博弈主体集合I、策略集合S、收益μ、均衡扰动函数ξ及停止准则τ。对于一般的组合优化问题,确定该算法的5个要素就可以转化为一个纯策略的多人非合作博弈问题。该算法中的5元素定义如下:
将局部融合系统中的每个传感器节点i映射为一个参与博弈的主体,则所有同质传感器节点构成博弈主体集合I=﹛1,2,…,n﹜,其中n为簇内成员节点数;si∈[0,1],i∈I表示博弈主体i的策略集,则在某一博弈回合中,主体选择的策略si做出对应的传输策略,n个主体的策略组合s就对应于公式(5)中的一个候选解x;在簇内信息融合博弈中,为各博弈主体设置相通的效用函数,均为f(x),即

当各个主体均无法选择更优的行动来更新系统状态,即整个系统达到了纳什均衡时。为了避免仅获得局部最优情况,通过随机方式对该稳定状态进行扰动,使其再次回归到不稳定状态。该文均衡扰动函数ξ定义如下:首先主体i通过rand(0,1)生成随机数ai;接着比较ai与算法设定的扰动概率ρd,若ai<ρd,则随机选择主体i的策略集中的一个元素,替换当前策略si;否则,维持原策略不变。所有主体经过上述过程后得到扰动后的新的策略组合s′。整个系统经过若干回合的从稳定到不稳定的扰动与恢复不断重复,最后各博弈主体始终构成某一固定的策略组合,则该策略组合构成一定稳定状态。算法的停止准则τ采用指定的采样周期停止算法。
根据关于Nash定理可知,局部融合博弈必存在至少一个Nash均衡点。即公式存在全局最优解x*使得μi(s*)≥μi(s),即f(x*)≥f(x)。显然,全局最优解并不是唯一的。这些全局最优解构成集合﹛x*﹜,由其中的点构成的策略组合都能使得加权博弈达到Nash均衡状态。当达到Nash均衡时,融合博弈中的各主体均获得最优的效用,这表示能通过计算得到一种最优的节点传输组合方案,达到网络效益最大。
2.3 DFEAMG算法流程
按一定规则获得初始的融合博弈结构,包括博弈主体集、策略集和效用函数集的确定。对每个博弈主体,通过模仿、学习确定其在本轮博弈中的策略,并根据效用函数计算各主体的效用。博弈个体通过改变策略增加效用,并根据评估函数对本轮博弈局势作出评价,判断是否达到纳什平衡,算法流程见图1。
算法将簇内节点传输策略组合优化问题的解空间映射到多人博弈的策略组合空间,通过主体的联盟效用最大化行为达到一个纳什均衡,并通过对均衡状态施加扰动而重新到达均衡。纳什均衡状态下的问题解称为纳什均衡解。如果新的纳什均衡解比上一回合寻找到的纳什均衡解更优,则更新,否则舍弃该解。通过上述的过程最终到达全局最优解。这里系统状态和效用函数是主体的共同知识,主体的理性行为指的是主体将会倾向于选择使自己效用最大的策略。算法中“纳什均衡解更优?”的判断是必要的,这样下一个纳什均衡解建立在前一个纳什均衡解得基础上。

图1 算法流程图
3 仿真实验
3.1 实验参数
通过采用MATLAB作为仿真平台进行模拟实验验证DFEAMG算法的性能。为了简化仿真实验参数,假设前提如下:
(1)假设在较为理想的信道条件下忽略干扰和信号冲突等随机因素的影响;
(2)假设节点一经部署完毕位置固定,节点能量小于(0.0000000001*Eo)则表示失效,无法进行工作;
(3)假设网络中的有效节点剩余10%时网络的覆盖度和连通度大幅度减低,网络不可用算法终止。
实验参数如表1,能量消耗模型参照参考文献[1]。

表1 实验参数表
由于目前还没有标准的通用的数据集,实验首先利用自行构造的模拟数据验证算法的可行性,从网络生存周期,网络能量消耗及融合结果精确度等,验证DFEAMG算法的优劣性。因为DFEAMG 是UCLC、MRPSO的改进算法,实验只选择LEACH,MRPSO作为对比算法。
实验设定某一固定值为参考点,代表待观测对象的真实值;用不同的百分比表示参与融合的各传感器节点的观测误差范围及邻居节点相似度范围。根据误差概率,采用随机的方法,产生围绕固定值上下波动的数组,用以模拟表示若干个精度不同的传感器节点在一定采样周期中对同一对象的观测数据。生成数据的主要参数包括实际测量参考值z、节点数n、采样周期数m(随机在网络的生存周期中取出若干个测量数据比较)、各节点的误差概率γ=﹛γ1,γ2,…,γn﹜和邻居节点相似度λ= ﹛λ1,λ2,…,λn﹜
测试数据产生规则:每个采样周期k(k=1,2,…,m),节点i(i=1,2,…,n)按如下规则产生模拟的测试数据zik:

则其邻居节点j产生的测试数据如下:

3.2 实验结果分析
在上述网络仿真环境下,采用自行生成的模拟数据进行实验。
实验1比较的是DFEAMG、MRPSO、LEACH3种不同算法相应的网络生存周期情况。图2显示的是网络中失效节点的数量随时间变化的情况。3个算法的网络生命周期分别是1145、975、580左右。MRPSO的网络生存周期比LEACH的延长了68%,而DFEAMG的比LEACH的延长了97%,将近一倍。DFEAMG算法比MRPSO的延长了170个生存周期左右。出现这种现象的原因是DFEAMG算法在MRPSO分簇路由中结合了簇内信息融合技术,不仅实现了簇间路由能量的优化,更进一步减少簇内节点的能量消耗。从图上可以看出MRPSO和DFEAMG的第一个节点和最后一个节点失效时间的跨度差不多,曲线都呈急速上升状。这说明DFEAMG与MRPSO一样,网络中的节点实现了能耗均衡。
图3描述的是从第475~525个采用周期中LEACH、MRPSO、DFEAMG 3种算法每轮网络中节点能量消耗总和情况。由图可知,采用LEACH算法的网络能量平均消耗最高,每个周期能量消耗范围[0.05,0075],波动范围最大。MRPSO每轮网络中节点能量消耗总分布范围在[0.048,0.054],而DFEAMG的分布在[0.42,0.0475]。DFEAMG的能量消耗总和是3种算法中最少的,而且数值分布范围最小。出现这种现象是因为MRPSO算法只有进行了簇间路由优化减少簇首转发数据的能耗,而DFEAMG通过簇内信息融合减少,减少了整个网络的数据传输量,真正实现了整个网络的能量优化。
实验2比较DFEAMG和MRPSO两种不同算法经过数据融合后最终结果的相似度。实验在网络的生命周期内随机抽取50个周期的融合数据进行对比。表2给出的是在不同允许的误差范围内两种算法得到融合结果的相似度。假设z1、z2分别表示网络采用DFEAMG和MRPSO算法进行融合后的最终感知数据。η表示这两种感知数据之间的误差,计算公式如(10)。

由表2可知,当误差d≤0.0005*z是DFEAMG与MRPSO融合结果相似度为88%。当误差为d≤0.001*z是DFEAMG与MRPSO融合结果相似度为98%。这证明了DFEAMG算法对系统融合结果的精确度并无很大影响。出现这种现象的原因是DFEAMG算法中参与数据融合的数据满足最小偏差,这样可以防止因为测量精度问题导致测量数据与其他节点的差别很大的节点参与数据融合影响最终的结果,从某种意义上说DFEAMG的最终融合比传统的均值融合更贴近实际值。结合图3可以证明DFEAMG不仅实现了簇内能量消耗优化同时也保证了融合结果精确性。
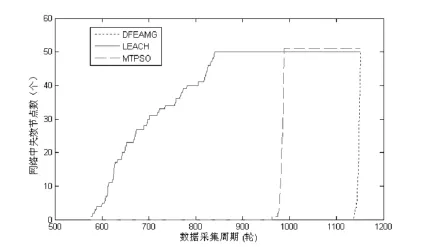
图2 网络生存周期

图3 每个周期能量消耗
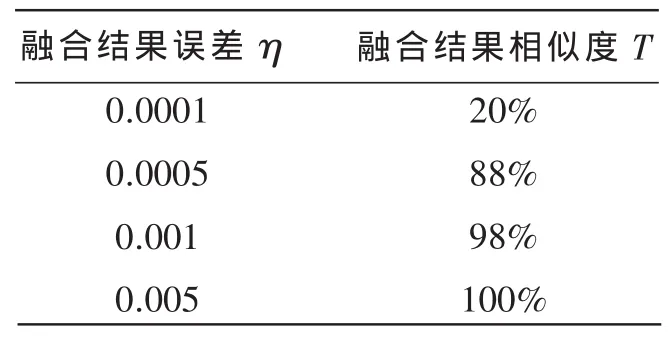
表2 融合结果比较
4 小结
通过将簇内节点竞争传输过程映射为为同质传感器间的多人博弈过程。DFEAMG仅依赖于当前各节点的观测数据和邻居节点的相关信息,克服了其他加权算法需要部分先验知识以及具有主观性的缺陷。实验结果表明,算法很好的均衡了网络中簇内能量消耗优化问题与融合结果精确度的问题,实现了簇内能耗优化,延长了网络生存周期并同时保证了网络融合结果的精确性。
[1]孙利民,李建中,陈渝,等.无线传感器网络[M].北京:清华大学出版社,2005.
[2]SHIH E,CHO SH,ICKES N,et al.Physical layer driven protocol and algorithm design for energy-efficient wireless sensor networks[C]//Proceedings of the 7th Annual International Conference on Mobile Computing and NetworkingRome:Association for Computing Machinery,2001.
[3]CRULLER D,ESTRIN D,SRIVASTAVA M.Overview of sensor networks[J].Computer(Long Beach,CA),2004,37 (8):41-49.
[4]托马斯L C.对策论及其应用[C].天津:解放军出版社,1988.
[5]GILBOA I,MATSUI A.Social stability and equilibrium[J].Econometrical,1991,59:859-867.
[6]FELEGYHAZI M,HUBAUX J P,BUTTYAN L.Nash equilibria of packet forwarding strategies in wireless Ad hoc networks[J].IEEE Transactions on Mobile Computing,2006,5(5):463-467.
[7]徐敏.基于博弈思想的优化算法研究[D].合肥:中国科技技术大学,2005.
[8]RENITA MACHADO,SIRIN TEKINAY.A survey of game-theoretic approaches in wireless sensor networks[J]. Computer Networks,2008,52:3047–3061.
[9]VON NEUMMAN,MORGENSTERN O.Theory of games and economic behavior[M].2nd ed.Princeton:Princeton University Press,1947.
[10]GUPTA G,YOUNIS M.Load-balanced clustering of wireless sensor networks[J].Proceeding of IEEE International Conference on Communications,2003(3):1848-1852.
[11]LI C F,CHEN G H,WU J.EECS:an energy efficient clustering scheme in wireless sensor networks[C]//The 24th IEEE International Performance,Computing,and Communications Conference,2005.
[12]AKYILDIZ I,SU W,SANKARASUBRAMANIAM Y,et al.Wireless sensor networks:a survey[J].Computer networks,2002,38(4):393-422.
[13]DAVID C,DEBORAH E,MANI S.Overview of sensor network[J].IEEE Computer,2004,37(8):41-49.
[14]张锐戈,陈善继.基于宽带源的单矢量传感器参数估计[J].三明学院学报,2008,25(2):154-157.
An Algorithm of Inter-cluster Data Aggregation Based on Multi-players Game Theory in Wireless Sensor Networks
CHEN Yi-ping
(Department of Computer Engineering,Zhicheng College,Fuzhou University,Fuzhou 350002,China)
Based on the analysis of the competition and cooperation between nodes by multi-players game theory,an algorithm of inter-cluster data aggregation is proposed in this paper.Simulations are taken to evaluate the performance of energy consumption balance,network lifetime and the precision of the aggregate data,and the results prove the effectiveness of this algorithm.
wireless sensor networks;data aggregation;game theory
TN929.5
A
1673-4343(2013)04-0024-06
2013-04-10
陈亦萍,女,福建莆田人,助教。研究方向:PSO智能算法、博弈论。

