有限粒子数效应对任意维量子气体热力学性质的影响
陈礼炜
(三明学院机电工程学院,福建三明365004)
有限粒子数效应对任意维量子气体热力学性质的影响
陈礼炜
(三明学院机电工程学院,福建三明365004)
对于束缚在任意维谐振势中的理想玻色气体和费米气体,有限粒子效应对其热力学性质将会产生影响。估计出在不同的情况下,有关于各个热力学量的相对修正。并对两种受限量子气体所得结果进行比较,得出结论:有限粒子数效应对于凝聚状态下的玻色气体(玻色气体在系统中发生玻色爱因斯坦凝聚)的影响要比费米气体和正常的玻色气体(没有发生玻色爱因斯坦凝聚的玻色气体)显著得多。
量子气体;有限粒子数;谐振势;热力学性质
近年来,人们对于对限尺度系统的热力学性质的研究产生了广泛的兴趣[1-6]。这在一定程度上推动了介观物理与纳米技术的发展。在真实的系统中,例如在实验中观察玻色爱因斯坦凝聚(BEC)[7-9]以及费米气体的简并[10],原子通常是被束缚在随着外势变化的空间中。在一般情况下,受限的粒子数量是有限的,所以受限系统的有限粒子数效应对其性质的影响被广泛地进行研究[11-14]。在本文中,将把前人的工作推广到D维谐振势束缚的量子气体系统,并且比较有限粒子数对于受限的玻色气体和费米气体特性影响的区别。研究结果表明,有限粒子数效应对于凝聚状态下的玻色气体(玻色气体在系统中发生玻色爱因斯坦凝聚)的影响要比费米气体和正常的玻色气体(没有发生玻色爱因斯坦凝聚的玻色气体)显著得多。
1 费米气体和正常玻色气体的热力学量的一般表达式
首先考虑没有相互作用的量子气体束缚在D维谐振势中,其中D维谐振势沿着方向i的频率为ωi(i=0,1,2,…,D),单粒子能级表达式为

其中ħ=h/2π,h为普朗克常数。
假设巨正则系综可以有效的描述所研究的系统,这是一个非常重要的假设。严格地说,正则系综理论可能更适合于真实的实验装置,其中粒子数量是基本固定的。由于这个原因,正则系综的处理方法被广泛地应用于有限量子气体系统[15-16]。对于有些统计量的涨落幅度,用两种系综处理之后,却有可能产生显著的差异[15]。然而,从两种系综出发所得到的热力学量的差别与由分立能谱产生的有限尺度效应相比却是相对微小的,例如基态粒子数N0。因此,巨正则系综仍然被广泛应用于小系统的尺度效应的研究[11-14]。
在巨正则系综中,系统的巨配分函数Ξ可以表达为

其中β=1/kBT,kB是玻尔兹曼常数,T是温度,z=exp(βμ)是逸度,μ是系统的化学势。为简单起见,与粒子内部结构有关的简并暂不考虑。在之前以及之后的方程中,上面的符号代表的是玻色系统,下面的符号代表的是费米系统。
按照通常的处理方法,在热力学极限条件下,就是将(2)式中的求和符号换成积分符号,便可以轻松的得到巨配分函数的表达式。然而,在粒子数有限的情况下,这种处理方法可能会导致显著的偏差。有关于对巨配分函数的计算,一种更加精确的处理方法是应用欧拉-麦克劳林公式,如式(3)[17]。
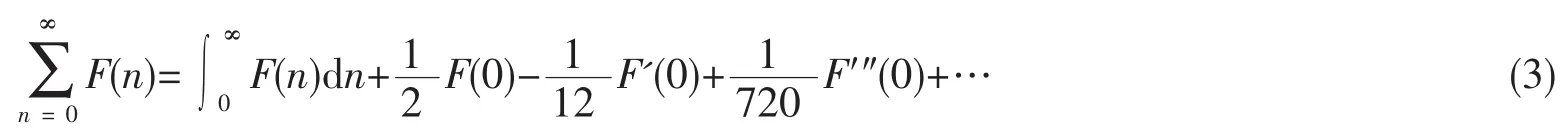
只考虑由于有限粒子数效应引起的第一项非零修正,可以得到巨配分函数的表达式
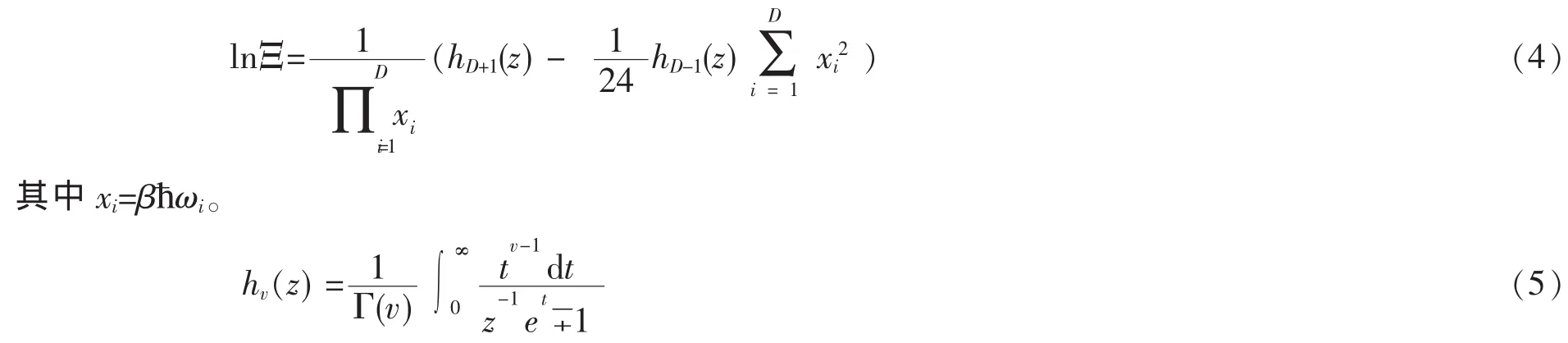
其中Γ(v)是伽玛函数。注意到方程(4)中不包含基态的贡献,且仅对费米气体和正常的玻色气体有效。有关于凝聚状态下的玻色气体的性质,将在第4节单独讨论。
在费米气体和正常的玻色气体的情况下,对于任意取值的v,hv(z)是收敛的。这个问题可以这样解释:对于费米气体,hv(z)可以简化为费米积分fv(z)[18],对于在0<z<∞范围内的任意值v,它的值是收敛的。对于玻色气体,hv(z)简化为玻色积分gv(z)[18],对于任意的v,在0<z<1范围内收敛,当v≤1时z=1,玻色积分的值发散。对于正常的玻色积分,即v为在0<z<1范围内的任意值,gv(z)是收敛的。
从巨配分函数出发,可以很容易地得到系统的热力学量。例如,可以分别得出内能E,比热C的表达式如(6)~(7):
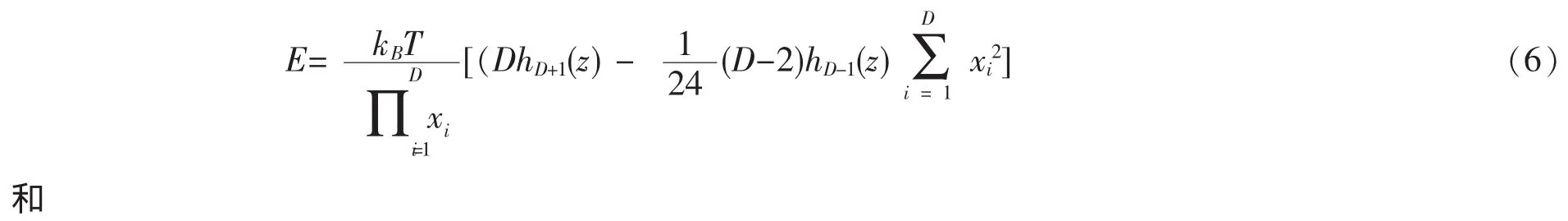
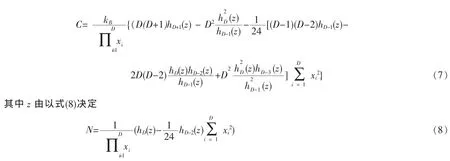
为了更清晰地表达有限粒子数效应对于热力学量的修正,引进一个系数z0,使得z0满足

可以很容易看出z0是系统处于热力学极限近似情况下的逸度。从方程(8)和方程(9)出发,仅仅保留到xi的二次方项,可以得出:

通过方程(6)(7)(9)和(10),可以分别得出系统的内能和热容的表达式。
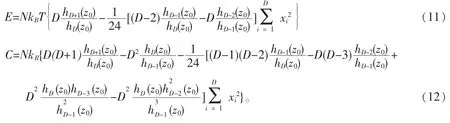
以上推导中,仅仅考虑了有限粒子数效应的一级非零修正项,忽略了有关于xi的两级以上的修正。从方程(3)可以得出,被忽略的第一个非零项包含了xi的三次方项,这意味着,以上所得结论的误差的数量级为N-3/D。
2 强简并费米气体的情况
对于强简并的费米气体,lnz0>>1,通过索末菲引理,方程可以展开为
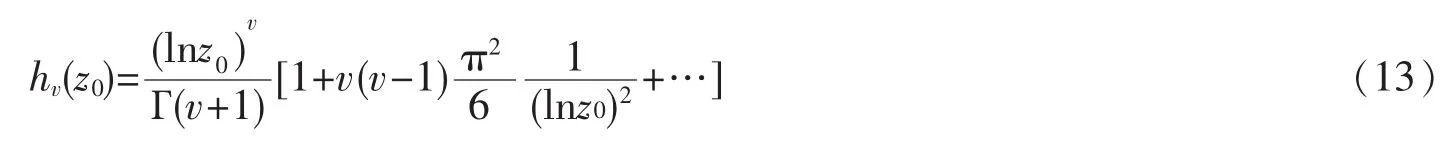
通过方程(13),可以得出内能E和热容C的表达式如式(14)和(15)。


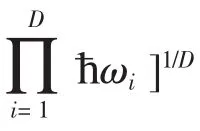
3 强简并情况下的玻色气体
在玻色系统中,当玻色-爱因斯坦凝聚发生时,即基态粒子数N0>>1,基态的贡献将不能被忽略,因此在第2节中所给出的结果将不再适用。通过进一步对基态的考虑,玻色气体的巨配分函数Ξ可以表示为
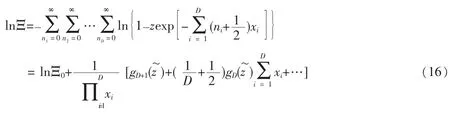

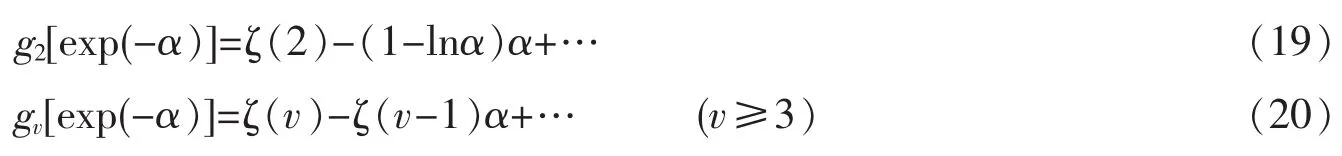
再加上方程(17)(18),可以得出
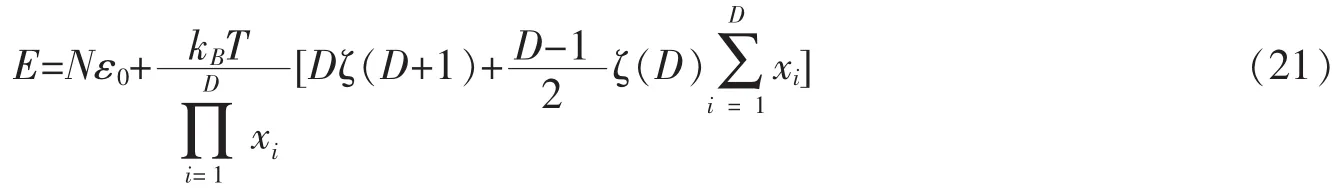
其中,只考虑了有限粒子数效应的一级修正项。通过方程(21),可以容易地得到热容的表达式
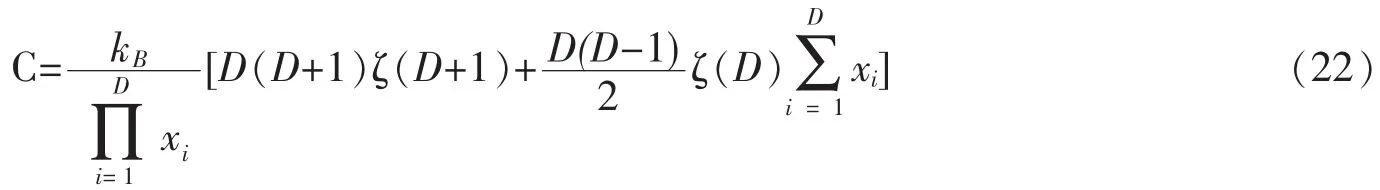
以上的结果仅仅对D≥2成立,因为,对于D=1,ζ(D)的值会发散。对于理想玻色气体束缚在一维的谐振势中,它的巨配分函数Ξ的表达式如式(23)所示
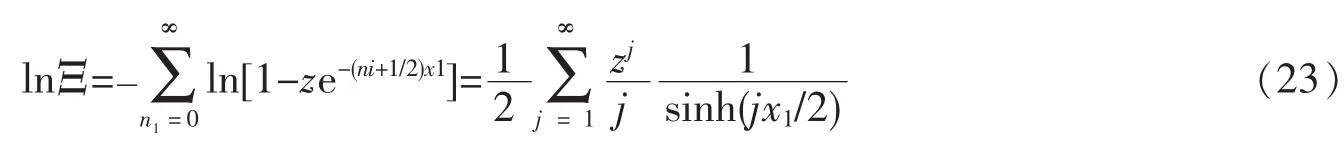
由此求出总粒子数和内能的表达式分别为(24)(25)。

方程(24)(25)可以运用数值计算,探讨有限粒子数效应对于气体性质的影响[12]。
对于一维凝聚的玻色气体,z→exp(x1/2)是不合理的,因为这会导致大约1/N0的相对误差,这与有限粒子数引起的相对修正是同一个数量级的。因此,如何解析得到其有限粒子数的修正是后续需要研究的问题。
值得注意的是在本节和第2节中所得到的对于玻色气体的解析结果不能涵盖在凝聚温度附近的情况。这不像在无限的系统中存在一个极限临界点,在有限的系统中相变温度附近的物理量在某一特定的区间内,可能变化得非常平稳。在这个区间内,与温度有关的物理量要比其它的区间复杂得多,这个问题在参考文献[14]中有做具体的讨论。
4 讨论
为了更清晰地展示有限粒子数效应对两种受限量子气体性质的影响,如图1所示,绘制了在各向同性的谐振势束缚下,热容随温度变化的特性曲线。图1(a)和(b)分别表示费米气体和玻色气体。图中实心方形点表示的是本文所得的解析结果;实线是严格的数值计算,对各量子态求和所得出的结果;虚线是在热力学极限条件下所得结果。可以清晰地看出对于费米气体和正常的玻色气体,由于有限粒子数效应引起的热容修正非常的小,只有在放大的插图中才能看到。然而,对于凝聚状态下的玻色气体,有限粒子数效应对于热容的修正相对较大,可以在主图中直接看到。从图中还可以看出,本文所得到的解析解与数值计算所得结果十分吻合,它们的差别即使在放大的图中也难以分辨。
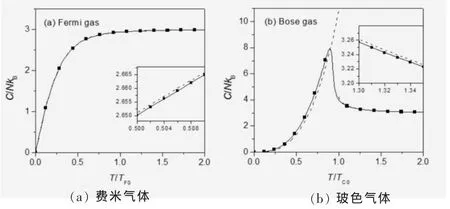
图1 热容随温度变化的特性曲线
图1对于费米气体和玻色气体,在粒子数为1000的情况下,热容随温度的变化曲线。实心方点、实线和虚线分别表示本文所得到的解析结果,严格的数值计算和热力学极限条件下所得结果。
5 结论
本文研究了理论量子气体束缚在D维谐振势中的热力学性质,讨论了有限粒子数效应对于系统性质的影响,估算出在不同情况下,有限粒子数效应引起的热力学量的修正的数量级,展示了对于玻色气体和费米气体的区别。得出对于凝聚的玻色气体,有限粒子数效应要比对于费米气体和正常的玻色气体显著得多。
[1]SISMAN A,MULLER I.The Casimir-like size effects in ideal gases[J].Phys Lett A,2004,320:360.
[2]SISMAN A.Surface dependency in thermodynamics of ideal gases[J].J Phys A:Math Gen,2004,37:11353.
[3]PANG H,DAI W S,XIE M.The difference of boundary effects between Bose and Fermi systems[J].J Phys A:Math Gen,2006,39:2563.
[4]DAI W S,XIE M.Quantum statistics of ideal gases in confined space[J].Phys Lett A,2003,311:340.
[5]DAI W S,XIE M.Geometry effects in confined space[J].Phys Rev E,2004,70:016103.
[6]BEGUN V V,M I.Gorenstein,Bose-Einstein condensation in the relativistic pion gas:Thermodynamic limit and finite size effects[J].Phys Rev C,2008,77:064903.
[7]ANDERSON M H,ENSHER J R,MATTHEWS M R,et al.Cornell,observation of Bose-Einstein condensation in a dilute atomic vapor[J].Science,1995,269:198.
[8]BARADLEY C C,SACKETT C A,TOLLETT J J,et al.Evidence of Bose-Einstein condensation in an atomic gas with attractive interactions[J].Phys Rev Lett,1995,75:1687.
[9]DAVISK B,MEWES M O,ANDREW M R,et al.Bose-Einstein condensation in a gas of sodium atoms[J].Phys Rev Lett,1995,75:3969.
[10]DEMARCO B,JIN D S.Onset of fermi degeneracy in a trapped atomic gas[J].Science,1999,285:1703.
[11]GROSSMANN S,HOLTHAUS M.On Bose-Einstein condensation in harmonic traps[J].Phys Lett A,1995,208:188.
[12]KETTERLE W,VAN DRUTEN N J.Bose-Einstein condensation of a finite number of particles trapped in one or three dimensions[J].Phys Rev A,1996,54:656.
[13]LIGARE M.Numerical analysis of Bose-Einstein condensation in a three-dimensional harmonic oscillator potential[J]. Am J Phys,1998,66:185.
[14]PATHRIA R K.Bose-Einstein condensation of a finite number of particles confined to harmonic traps[J].Phys Rev A, 1998,58:1490.
[15]GLAUM K,KLEINERT H.Condensation of ideal Bose gas confined in a box within a canonical ensemble[J].Phys Rev A,2007,76:063604.
[16]WANG J,MA Y.Thermodynamics and finite-size scaling of homogeneous weakly interacting Bose gases within an exact canonical statistics[J].Phys Rev A,2009,79:033604.
[17]ABRAMOWITZ M,STEGUN C A.Handbook of mathematical functions with formulas,graphs,and mathematical tables [M].New York:Dover,1972.
[18]PATHRIA R K.Statistical mechanics[M].Oxford:Pergamon Press,1972.
The Effects of a Finite Number of Particles on Two Trapped Quantum Gases
CHEN Li-wei
(Mechanic and Electronic Engineering College,Sanming University,Sanming 365004,China)
The effects of a finite number of particles on the thermodynamic properties of ideal Bose and Fermi gases trapped in any dimensional harmonic potential are investigated.The orders of relative corrections to the thermodynamic quantities due to the finite number of particles are estimated in different situations.The results obtained from the two trapped quantum gases are compared,and consequently,it is shown that the finite-particle-number effects for the condensed Bose gas (a Bose gas with BEC occurring in the system)are much more significant than those for the Fermi gas and normal Bose gas (a Bose gas without BEC).
quantum gas;finite particle number;harmonic potential;thermodynamic
O413.1
A
1673-4343(2013)04-0001-06
2013-04-29
三明学院科研基金项目(B201202/G)
陈礼炜,女,福建永安人,讲师,博士。研究方向:统计物理,工程热力学,清洁能源利用。

