与对合矩阵可交换的反对合矩阵
王洁,黄益生
(三明学院信息工程学院,福建三明365004)
与对合矩阵可交换的反对合矩阵
王洁,黄益生
(三明学院信息工程学院,福建三明365004)
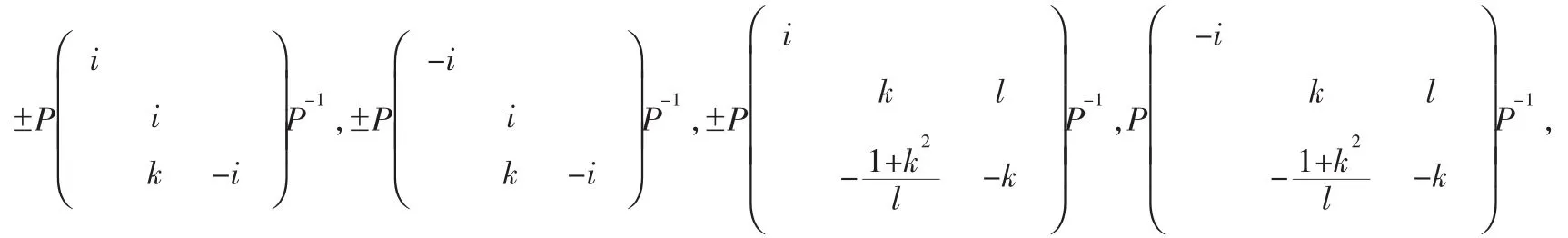
对合矩阵;反对合变换;矩阵的相似关系;特征值
众所周知矩阵的乘法不满足交换律。讨论两个矩阵的乘积是否可交换的问题,历来是矩阵论中的热门话题。近年来,这方面的研究文章仍然时有出现。在文献[1]中,作者讨论了与对称矩阵可交换的反对称矩阵。在文献[2]中,作者讨论了这个问题的反问题,即与反对称矩阵可交换的对称矩阵。在文献[3]中,作者讨论了对合矩阵与反对合矩阵的有关性质。在本文中将初步探讨与对合矩阵可交换的反对合矩阵。主要结果如下:
(1)给出了与n阶对合矩阵可交换的反对合矩阵的一种表示;
(2)对于2阶对合矩阵A,如果A≠±I(I是单位矩阵),那么与A可交换的反对合矩阵一共有4个,它们是±iI和±iA;
(3)对于3阶对合矩阵A,如果A≠±I,那么与A可交换的全体反对合矩阵为±iI和±iA,以及
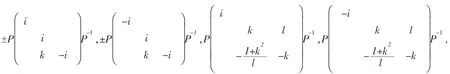
其中k是任意复数,l是任意非零复数;当tr(A)=-1时,P是A与diag{1,-1,-1}这一对相似矩阵之间的相似因子;当tr(A)=1时,P是A与diag{-1,1,1}之间的相似因子。
本文引用文献[4~5]的符号、术语和结论,不再另加说明。
定义[3]设A是数域F上的一个n阶方阵。若A2=I,则称A为一个对合矩阵;若A2=-I,则称A为一个反对合矩阵,这里I是n阶单位矩阵。
根据上述定义,不难看出,在任意数域上,对合矩阵都有特征值,其特征值只能为1或-1,在复数域上,反对合矩阵的特征值只能为i或者-i。
命题1[6]设A是数域F上的一个n阶对合矩阵。如果A一个特征值为1(或-1),那么它只能是n阶单位矩阵I(或I的负矩阵-I);如果A既有特征值1,又有特征值-1,那么它相似于准对角矩阵diag{Ir,-In-r},这里r是特征值1的几何重数,Ir是r阶单位矩阵。
注意到diag{Ir,-In-r}实际上是一个对角矩阵,根据命题1,每一个n阶对合矩阵(在任意数域上)都可对角化。下面的命题2表明,每一个n阶反对合矩阵(在复数域上)都可对角化。
命题2[7]设A是复数域上的一个n阶对合矩阵。如果A只有只有一个特征值为i(或-i),那么它只能是纯量矩阵iI(或-iI);如果A既有特征值i,又有特征值-i,那么它相似于准对角矩阵diag {iIr,iI},这里r是特征值1的几何重数,Ir是r阶单位矩阵。
命题3在复数域上,全体2阶反对合矩阵可以分成5种类型:
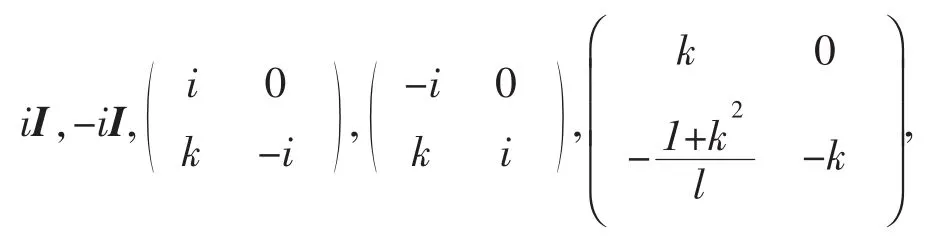
其中I是2阶单位矩阵,k是任意复数,l是任意非零复数。
证明:设A是一个2阶反对合矩阵。根据命题2,A是可对角化的,并且它的两个特征值只能为i 或-i。如果A的特征值全为i,因为A是可对角化的,特征值i的几何重数等于2,从而iI-A的秩等于零,因此iI-A是零矩阵,即iI-A=0,故A=iI。类似地,可以证明,如果A的特征值全为-i,那么A=-iI。
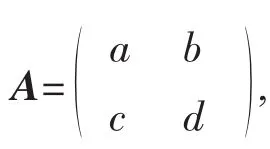

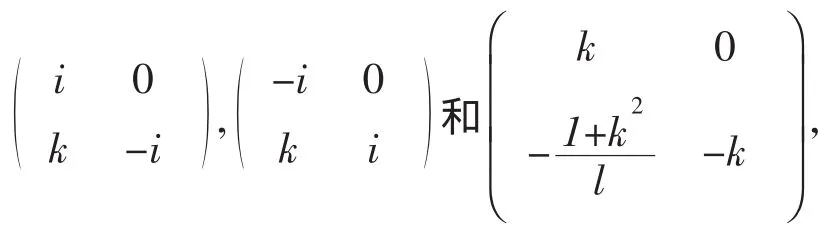
另一方面,容易验证,上述5类矩阵都是反对合的(其中iI和-iI这两个矩阵各自构成一个类)。因此在复数域上,全体2阶反对合矩阵可以分成上述5种类型。
下面讨论与对合矩阵可交换的反对合矩阵。
设A是复数域上的一个n阶对合矩阵。根据命题1,矩阵A相似于diag{Ir,-In-r},其中r是特征值1的几何重数,当r=n时,有A=I,当r=0时,有A=-I。显然,对于这两种情形,每一个n阶反对合矩阵都与A可交换。不妨设r≠n且r≠0。因为A相似于diag{Ir,-In-r},存在一个n阶可逆复矩阵P,使得P-1AP=diag{Ir,-In-r},即A=Pdiag{Ir,-In-r}P-1。设X是与A可交换的反对合矩阵,则AX=XA,即

由最后一个等式,容易验证Y是形如diag{B1,B2}的准对角矩阵,其中B1是一个r阶小方阵,B2是一个nr阶小方阵。已知X是反对合的,那么由Y=P-1XP可见,Y也是反对合的。再由Y=diag{B1,B2},不难看出B1,B2都是反对合的。从而由X=PXP-1看到与A可交换的反对合矩阵可以表示成Pdiag{B1,B2}P-1,其中小方阵B1与B2都是反对合的。另一方面,设B1是一个r阶反对合矩阵,B2是一个n-r阶矩阵。令

容易验证,X是一个n阶反对合矩阵,并且A和X是可交换的。综上所述,得到定理1。
定理1设A是复数域上的一个n阶对合矩阵,并设r是特征值1的几何重数。
(1)如果r=n或r=0(即A=±I),那么每一个n阶反对合矩阵都与A可交换。
(2)如果0<r<n,那么与A可交换的反对合矩可以表示成Pdiag{B1,B2}P-1,其中B1是任意r阶反对合矩阵,B2是任意n-r反对合阶矩阵,P是A与diag{Ir,-In-r}这一对相似矩阵之间的一个相似因子。
利用定理1,可以求出与2阶对合矩阵或3阶对合矩阵可交换的全体反对合矩阵。
事实上,设A是复数域上的一个2阶对合矩阵。如果A≠±I,那么A的两个特征值为1和-1,。因为A是可对角化的,存在一个2阶可逆复矩阵P,使得

根据定理1,与A可交换的反对合矩阵为Pdiag{b1,b2}P-1,其中b1与b2是两个复数(1阶方阵)使得=-1,且=-1,所以b1=±i且b2=±i,因此与A可交换的反对合矩阵一共有4个,它们是Pdiag{±i,±i}P-1。这4个矩阵也可以写成±iPdiag{1,1}P-1和±iPdiag{1,-1}P-1,显然前者就是纯量矩阵±iI。由于A= Pdiag{1,-1}P-1,后者就是±iA。这就得到
推论1设A是复数域上的一个2阶对合矩阵。
(1)如果A=±I,那么每一个2阶反对合矩阵都与A可交换。
(2)如果A≠±I,那么与A可交换的反对合矩阵一共有4个,它们是±iI和±iA。
其次,设A是一个3阶对合矩阵。如果A≠±I,那么A的3个特征值为1,-1,-1或1,1,-1。因为A是可对角化的,当它的特征值为1,-1,-1时,存在一个3阶可逆复矩阵P,使得

根据定理1,与A可交换的反对合矩阵为Pdiag{b1,B2}P-1,其中=-1(即b1=±i),并且B2是任意2阶反对合矩阵。用±i代替Pdiag{b1,B2}P-1中的b1,并用命题3中5中类型的2阶反对合矩阵分别代替B2,就得到与A可交换的全体反对合矩阵,它们是
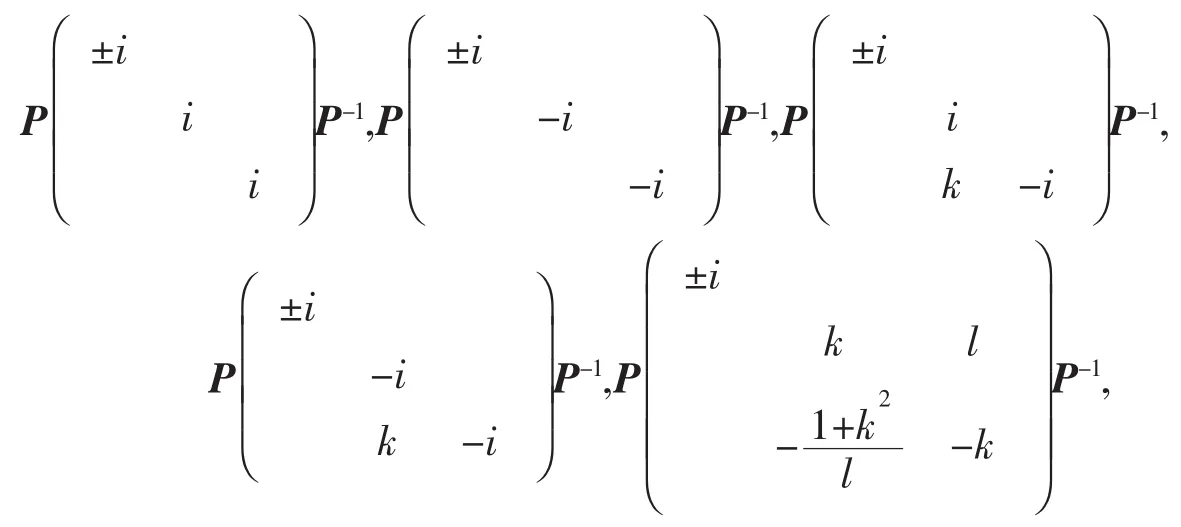
其中k是任意复数,l是任意非零复数。
考察前两类3阶反对合矩阵,不难看出,它们可以合并成±iI和±iPdiag{1,-1,-1}P-1。注意到A=Pdiag{1,-1,-1}P-1,因此这两类矩阵就是±iI和±iA。在考虑第三、四类两矩阵,由于k是任意复数(因而可以用-k代替k),这两类矩阵可以合并成

由此可见,上一段中的五类3阶反对合矩阵也可以表示成这一段中的六类矩阵。
当A的3个特征值为1,1,-1时,由于diag{1,1,-1}相似于diag{-1,1,1},根据矩阵相似关系传递性,A相似于diag{-1,1,1}。于是存在一个3阶可逆复矩阵,使得

与前面讨论类似,可以证明,与A可交换的反对合矩阵也是上一段中的6类矩阵,其中P是A与diag{-1,1,1}这一对相似矩阵之间的一个相似因子。
注意到当A≠±I,有tr(A)=±1,根据上面讨论因此得到:
推论2设A是复数域上的一个3阶对合矩阵。
(1)如果A=±I,那么每一个3阶反对合矩阵都与A可交换。
(2)如果A≠±I,那么与A可交换的反对合矩阵为±iI和±iA,以及
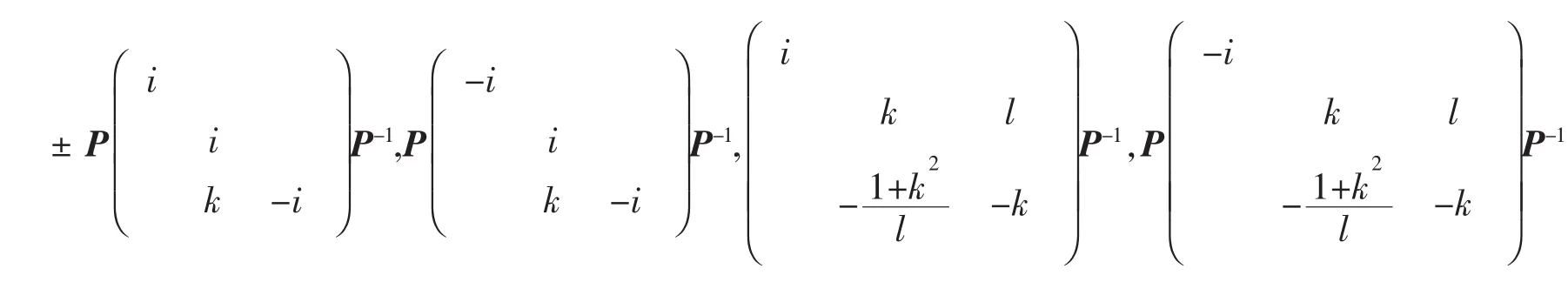
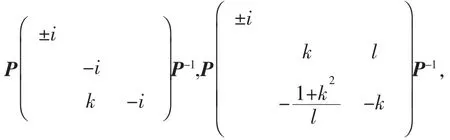
其中k是任意复数,l是任意非零复数;当tr(A)=-1时,P是A与diag{1,-1,-1}之间的一个相似因子;当tr(A)=1时,P是A与diag{-1,1,1}之间的一个相似因子。

则P是可逆的,并且P-1AP=diag{1,-1,-1}。经计算,有
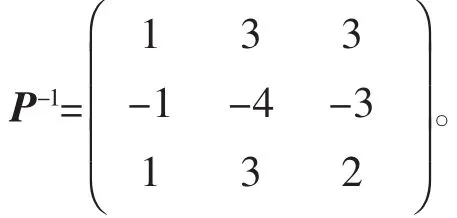
于是把所求的矩阵P和P-1代入推论2(2)后4类矩阵的表达式中,就可以求出与A可交换的全体反对合矩阵,它们是±iI和±iA,以及
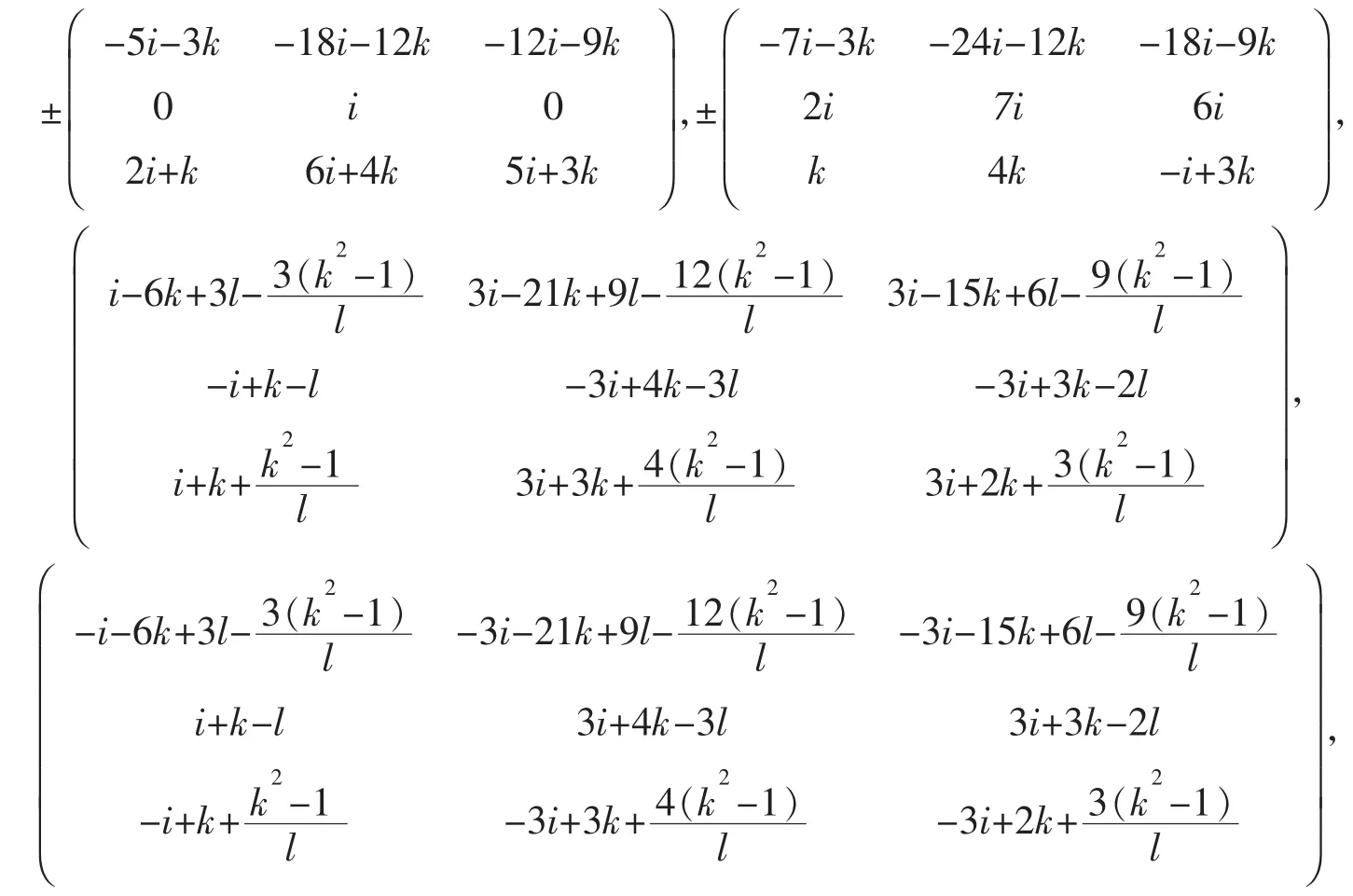
其中k是任意复数,l是任意非零复数。
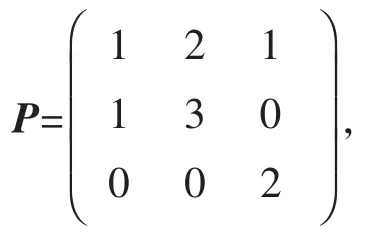
则P是可逆的,并且P-1AP=diag{-1,1,1}。经计算,有
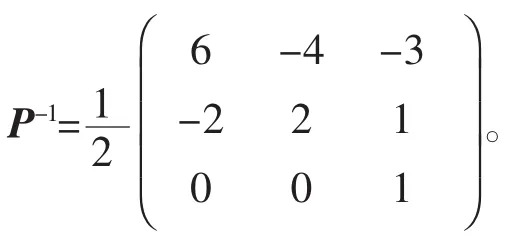
现在把所求的矩阵P和P-1代入推论2(2)后4类矩阵的表达式中,就可以求出与A可交换的全体反对合矩阵,它们是±iI和±iA,以及

其中k是任意复数,l是任意非零复数。
[1]黄益生,姚海鹭.与对合矩阵可交换的反对合矩阵[J].龙岩学院学报,2010,28(2):1-4.
[2]王春燕,李立等.与反对称矩阵可交换的对合称阵[J].齐齐哈尔大学学报,2011,27(6):79-82.
[3]邹本强.对合矩阵与反对合矩阵的若干性质[J].金华职业技术学院学报,2007,7(2):88-90.
[4]张禾瑞,郝鈵新.高等代数[M].4版.北京:高等教育出版社,1999.
[5]丘维声.高等代数[M].2版.北京:高等教育出版社,2003.
[6]董庆华,颜宁生.对合矩阵的相似标准形与分解形式[J].邵阳学院学报,2009,6(4):12-14.
[7]黄益生,陈椰婷.反对合矩阵的相似对角化[J].三明学院学报,2013,30(2):1-5.
Anti-Involutory Matrices which Are Involutory MatricesCommutative with
WANG Jie,HUANG Yi-sheng
(School of Information Engineering,Sanming College,Sanming 365004,China)
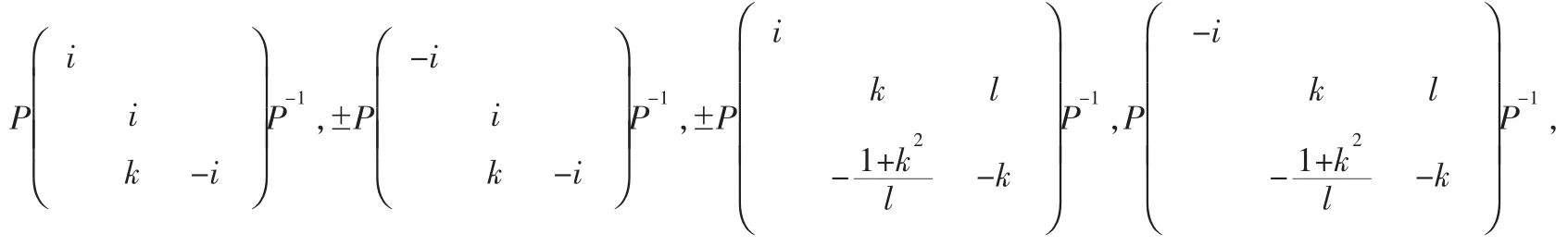
involutory matrix;anti-involutory matrix;similar relation of matrices;eigenvalue
O151.21
A
1673-4343(2013)04-0007-06
2013-01-20
福建省教育厅高等学校教学质量工程资助项目(ZL0902/TZ(SJ))
王洁,女,福建福安人,大学生;通讯作者:黄益生,男,福建龙岩人,教授。研究方向:代数。

