An Introduction to Transmit Antenna Selection in MIMOWiretap Channels

Nan Yang ,Maged Elkashlan ,Phee Lep Yeoh ,and Jinhong Yuan

(1.The University of New South Wales,NSW 2052,Australia;

2.Queen Mary,University of London,London E1 4NS,UK;

3.The University of Melbourne,VIC 3010,Australia)

Abstract This paper is a survey of transmit antenna selection—a low-complexity,energy-efficient method for improving physical layer security in multiple-input multiple-output wiretap channels.With this method,a single antenna out of multiple an⁃tennasisselected at thetransmitter.We review a general analytical framework for analyzingexact and asymptotic secrecy of transmit antenna selection with receive maximal ratio combining,selection combining,or generalized selection combin⁃ing.Theanalytical resultsprovethat secrecy issignificantly improved when thenumber of transmit antennasincreases.

Keyw ords physical layer security;transmit antennaselection;secrecy outageprobability;wirelessfading

1 Introduction

I nformation security is vital in wireless communications.The broadcast nature of the wireless channels allows potential eavesdroppers to intercept data transmitted in communication networks.Traditionally,cryptographic protocols provide security in the upper layers(e.g.the network layer),assuming that an error-free link has been created in the physical layer[1].In wireless networks,distributing and man⁃aging secret keys can be expensive and insecure[2].There⁃fore,research has recently been done on physical layer securi⁃ty,in which the characteristics of wireless channels are exploit⁃ed for secure data transmission.Pioneering works on physical layer security describe a wiretap channel with a single antenna at the transmitter,receiver,and eavesdropper[3]-[6].Perfect secrecy is achieved in wiretap channels when the quality of the transmitter-eavesdropper channel is lower than that of the transmitter-receiver channel[3]-[6].

Physical layer security in multiple-input multiple-output(MIMO)wiretap channels has been motivated by emerging wireless applications with multiple antenna terminals and has recently been addressed from the perspective of information theory[7]-[10].In[7]-[10],the secrecy capacity of a MIMO wiretap channel was determined.Wireless fading has also been considered[11]-[13].In[11]and[12],the secrecy outage probability was determined for Rayleigh fading,and in[13]and[14],the secrecy outage probability wasdetermined for Na⁃kagami-m fading.In[15]-[18],transmit beamforming(TBF)in the direction of the receiver was investigated as a way of secur⁃ing transmission in the MIMO wiretap channel.In[15],TBF was proposed to minimize the transmit power for a pre-speci⁃fied signal to interference plus noise ratio(SINR)at the receiv⁃er.In[16],artificial noise was incorporated into the beamform⁃ing weights to constrain the maximum SINRs of the eavesdrop⁃pers.In[17],linear precoding was done at the transmitter,which means a game-theory formulation was used to balance performance and fairness.In[18],codebook-based transmis⁃sion beamforming was for situations where receiver feedback capacity is limited.These TBF methods require precise infor⁃mation about the main channel and eavesdropper channel.Such information increases feedback overhead and computa⁃tion during signal processing,especially when there is a large number of transmit antennas[19],[20].

To reduce feedback overhead and computation introduced by TBF,and to increase physical layer security,transmit anten⁃na selection(TAS)can be applied at the multiantenna transmit⁃ter[21]-[25].In[21],TAS secrecy was analyzed for multi⁃ple-input,single-output(MISO)wiretap channels where the legitimate receiver has a single antenna.In[22]and[23],the secrecy of TAS with receive maximal-ratio combining(TAS/MRC)or selection combining(TAS/SC)was analyzed for gener⁃al MIMOwiretap channels.In[24],the effect of antenna corre⁃lation at the receiver and eavesdropper on TAS/MRC secrecy was determined.In[25],TAS with receive generalized selec⁃tion combining(TAS/GSC)was introduced into MIMO wiretap channels,and of TAS/GSCsecrecy wasthen determined.

In this paper,we focus on an important question:Is TASan effective method for improving physical layer security in MI⁃MO wiretap channels?We provide a survey on TASand show how TASbenefitstransmission security in MIMOwiretap chan⁃nels.In section 2,we discuss the properties of MIMO wiretap channels and describe the details of TASfor increased securi⁃ty.In section 3,we discuss exact TASsecrecy.In section 4,we discuss asymptotic TASsecrecy.In section 5,we provide fig⁃ures that show the effect of system parameters on secrecy.Sec⁃tion 6 concludesthepaper.

2 MIMO Wiretap Channels with TAS

2.1 MIMO Wiretap Channels

We consider a MIMO wiretap channel as shown in Fig.1[23].Specifically,the channel between Alice and Bob is the main channel,and the channel between Alice and Eve is the eavesdropper's channel.The eavesdropper is passive,which means there is no channel state information(CSI)feedback be⁃tween Alice and Eve,and Alice does not know the CSI of the eavesdropper's channel.Alice encodes her messages using wiretap codes and transmits the code words to Bob.Eve over⁃hears the information conveyed by Alice to Bob without induc⁃ing any interference in the main channel[26].We assume that both the main channel and the eavesdropper channel both ex⁃perience slow block fading and that fading coefficients do not vary during one fading block.We also assume that the block length is sufficiently long to allow for capacity-achieving codes within each block.Furthermore,the main channel and eavesdropper channel are assumed to have the same fading block length.Thesecrecy capacity isexpressed as[6]

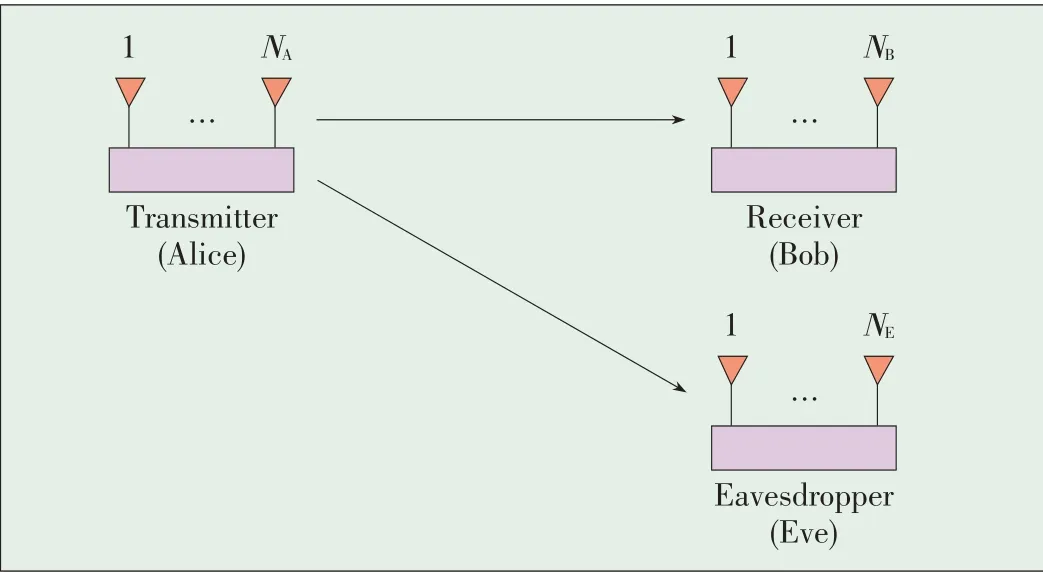
▲Figure1.MIMOwiretap channel with N A,N B,and N E antennas at Alice,Bob,and Eve,respectively.

Where CB=log2(1+γB)is the capacity of the main channel,and CE=log2(1+γE)is the capacity of the eavesdropper chan⁃nel.In(1),γBandγEdenote the instantaneous signal-to-noise ratios(SNRs)of the main channel and the eavesdropper chan⁃nel,respectively.In this paper,we focus on a scenario where the main channel and the eavesdropper channel are subject to independent but non-identically distributed(i.n.i.d.)Rayleigh fading.

2.2 Transmit Antenna Selection

Here,we describe a TAS protocol for the MIMO wiretap channel in Fig.1[23].This protocol is designed to boost CSby increasing CBrelative to CE.In the main channel,the strongest antenna of NAavailable antennas is selected in order to maxi⁃mize the instantaneous SNR between Alice and Bob and to se⁃curely transmit data.Therefore,as NAincreases,CBalso in⁃creases.Selecting the strongest antenna at Alice is optimal for secrecy because CBis maximized,and multiantenna diversity at the transmitter is fully exploited.In the eavesdropper chan⁃nel,the strongest transmit antenna for Bob is equivalent to a random transmit antenna for Eve.Therefore,as NAincreases,CEdoesnot increase.The TASprotocol has low feedback over⁃head because Bob only feeds back to Alice the index of the strongest antenna as well as the channel estimates associated with the strongest antenna.The index allows Alice to select the strongest transmit antenna,and the estimated CSIallows her to determine the size of the codebook with random binning(which is used for secure transmission)[6].The TASfeedback overhead is lower than TBF feedback overhead because TBF necessitates CSIfeedback for NAtransmit antennas.

The TAS protocol is well-suited to passive eavesdropping,where Alicedoesnot know the CSIof theeavesdropper'schan⁃nel.In such a case,Alice selects a constant code rate RS.If CB-CE＞RS,the code words with code rate selected by Alice guarantee secrecy.If CB-CE≤RS,Eve can eavesdrop,and secrecy is not guaranteed.In passive eavesdropping scenarios,secrecy outage probability isa useful metric for assessing secu⁃rity.

At Bob,we focus on three practical diversity-combining techniques:MRC,SC,and GSC.MRC is used to coherently combine the received signals when the number of implemented radio frequency(RF)chains is NB.SCis used to select the sig⁃nal with the highest instantaneous SNR when there is only one RF chain(because of size and complexity constraints).GSCis used to select and combine the signals of LBstrongest anten⁃nas out of NBavailable antennas when the number of imple⁃mented RF chains is LBfor 1＜LB＜NB.The NB×1 channel vector between the n th transmit antenna at Alice and NBanten⁃nas at Bob is given by hn,B=[hn,1,hn,2,…hn,NB]T,where[·]Tde⁃notes the transpose operation.The antennas at Bob have inde⁃pendent and identically distributed(i.i.d.)Rayleigh fading en⁃tries.When MRCis used at Bob,the index of the selected an⁃tenna is given by[23]where‖·‖denotes the Euclidean norm.When SC is used at Bob,the index of the selected antenna is given by[23]

The combining technique used at Eve depends on the num⁃ber of RF chains at Eve.MRC is optimal at Eve because the benefits of NEantennas are fully exploited,and the probability of successful eavesdroppingismaximized.

3 Analyzing Exact Secrecy

3.1 Secrecy Outage Probability

Here,we give closed-form expressions for the exact proba⁃bility of secrecy outage using TAS.This is the probability that the achievable secrecy rate CSis less than a predetermined se⁃crecy transmission rate RS.When CSis less than RS,secure transmission is not guaranteed.The secrecy outage probability is given by[6]

We proceed to the generalized framework for analyzing the secrecy outage probability.From(5),the secrecy outage proba⁃bility can also be given as[23]

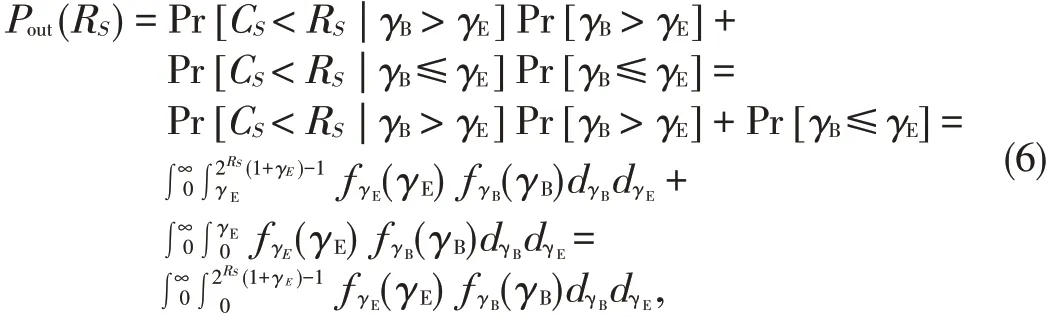
whereƒγB(γB)is the probability density function(PDF)ofγB,andƒγE(γE)is the PDF ofγE.Given the properties of Rayleigh fading channels and the diversity combining techniques used at Bob and Eve,ƒγB(γB)andƒγE(γE)can be easily obtained.

Here,we give the secrecy outage probabilities of TAS/MRC,TAS/SC,and TAS/GSC.In these expressions,we assume that Bob and Eve use the same diversity combining techniques.For TAS/MRC(TASis used at Alice,and MRCis used at both Bob and Eve),the secrecy outageprobability isgiven by[22]

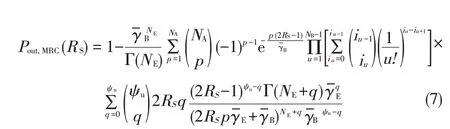
WhereγBandγEaretheaverageper-antennareceived SNRat Bob and Eve,respectively.In(7),for i0=p,and iNB=0.To obtain(7),we substituteƒγB(γB)andƒγE(γE)into(6);we use[27,eq.(1.111)]to expand the binomial;and we use[28,eq.(9)]to expand the resulting polynomial.Then,we solve the resulting integrals using[27,eq.(3.326.2)].If we follow this same procedure,the secrecy outage probability of TAS/SC(TASis used at Alice,and SCis used at both Bob and Eve)is given by[22]

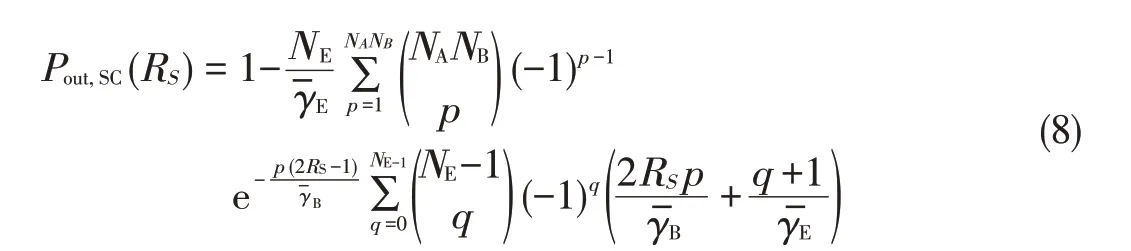
The secrecy outage probability of TAS/GSC(TASis used at Alice,and GSCisused at both Bob and Eve)isgiven by[25]

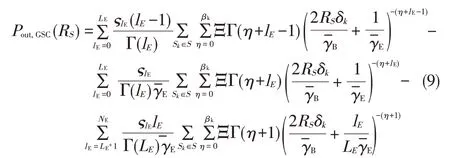
where S={Sk｜∑Nn=0nk,n=NA}with nk,n∈Z+and

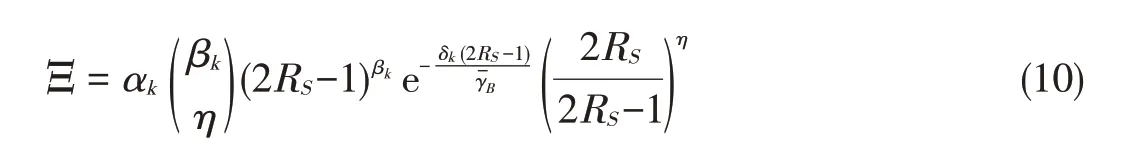
3.2 Probability of Nonzero Secrecy Capacity

Here,wedescribe thecondition for non-zerosecrecy capaci⁃ty.From(1),theprobability of nonzerosecrecy capacity is[6]

From(6)and(11),the relationship between Pout(RS)and Pr[C＞0]is Pr[C＞0]=1-P(0).Theprobabilities of nonzero

The definition ofςlEin(9)can be found in[29,eq.(3)].The definitions ofαk,βk,andδkin(10)can be found in[29,eq.(6)-(8)].The secrecy outage probability expressions in(7),(8),and(9)are closed-formexpression and apply to arbitrary num⁃bersof antennasand arbitrary average SNRs.secrecy capacity for TAS/MRC,TAS/SC,and TAS/GSCare ob⁃tained from(7),(8)and(9),respectively.

3.3ε-Outage Secrecy Rate

Theε-outage secrecy rate RSmaxis the maximum secrecy rate when the secrecy outage probability is less thanε[12].This rate is given byε=Pout(RSmax).Theε-outage secrecy rates for TAS/MRC,TAS/SC,and TAS/GSC can be obtained by apply⁃ingnumerical root-findingto(7),(8)and(9),respectively.

4 Analyzing Asymptotic Secrecy

4.1 Asymptotic Secrecy Outage Probability

We introduce the asymptotic secrecy outage probability to characterize secrecy outage probability when the average SNR of the main channel is sufficiently high;that is,when→∞.This corresponds to a scenario where Bob is much closer to Al⁃ice than Eve(which is an interesting practical scenario).The asymptotic secrecy outage probability allows us to determine the effects of antenna correlation on secrecy outage diversity order and secrecy outage array gain.The secrecy outage diver⁃sity order is the slope of the secrecy outage probability curve and describes how fast secrecy outage probability decreases with average SNR.The secrecy outage array gain is the hori⁃zontal shift of the secrecy outage probability curve.This gain describes the SNR advantage of a secrecy outage probability curve relative to the reference curve with the same secrecy out⁃agediversity order.

To introduce the asymptotic probability,we show the first nonzero order expansion of the cumulative distribution func⁃tion ofγB.This gives.Specifically,the first nonzero or⁃der expansion can be obtained by using the first order Maclau⁃rin series expansion from[27,eq.(1.211.1)]and neglecting the higher-order terms.UsingtheexpansionƒγE(γE)and(6),theas⁃ymptotic secrecy outage probability is given by[22]

where Gdis the secrecy outage diversity order and Gɑisthe se⁃crecy outagearray gain.For TAS/MRC,Gd,MRC=NANBand[22]

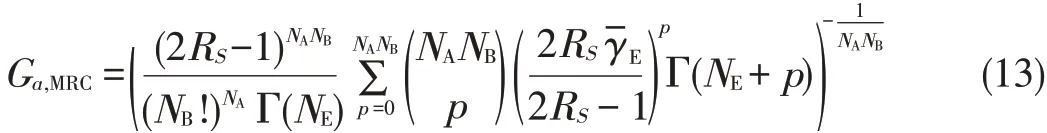
For TAS/SC,wehave Gd,SC=NANBand[22]

For TAS/GSC,Gd,GSC=NANBand[25]

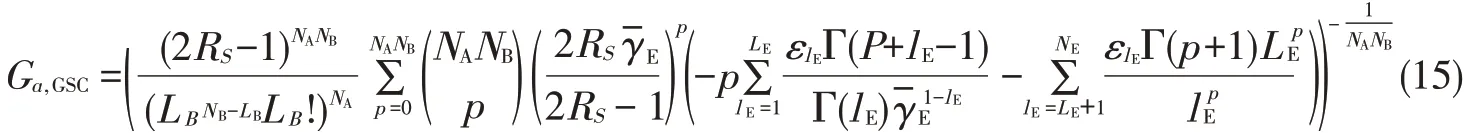
In light of these asymptotic results,we can make the follow⁃ing points about the use of TASwith MRC,SC,or GSC in the wiretap channel:

·The secrecy outage probability approaches zero asγBap⁃proaches infinity.

·TAS/MRC,TAS/SC,and TAS/GSC achieve the same secre⁃cy outage diversity order of NANB.This diversity order de⁃pendsentirely on themain channel.

·The secrecy outage diversity order of TAS/MRC,TAS/SC,and TAS/GSC is not affected by the eavesdropper channel.Moreover,the secrecy outage diversity order of TAS/GSC is not affected by the choice of LBor LE.

4.2 Secrecy Performance Tradeoff

Here,we discuss the secrecy outage tradeoff between TAS/GSC,TAS/SC,and TAS/MRC at the legitimate receiver.The asymptotic results show that this tradeoff is characterized sole⁃ly by secrecy outage SNR gain.When the same diversity com⁃bining technique is used at the eavesdropper,the SNR gap be⁃tween TAS/GSC and TAS/SC in the main channel is given by[25]

As LBincreases,Δ1＞0 and the SNR gap increases.The SNR gap between TAS/GSCand TAS/MRCisgiven by[25]

As LBincreases,the SNR gap decreases.By observingΔ1andΔ2,we find that these SNRgapsdepend entirely on NBand LB.They arenot affected by NEand LE.

5 Numerical Results

We now give numerical results that show how the number of antennas and average SNR affect secrecy.We normalize the varianceof thefadingcoefficientstounity.

In Fig.2[22],secrecy outage probability is plotted againsto show the effect of NAon secrecy.There isasignificant de⁃crease in the secrecy outage probability when NAincreases be⁃cause NAincreases the secrecy diversity order through NANB.This means that the secrecy outage probability quickly ap⁃proaches zero as NAincreases,and the probability of secure transmission issufficiently high.

In Figs.3 and 4[22],se outage probability is plotted agains to show the effect of NBand NEon secrecy,re⁃spectively.In Fig.3,secrecy outage probability significantly decreases as NBincreases because secrecy diversity or⁃der increases as N increases.In Fig.4,secrecy outage probability increases as NEincreases.This in⁃creases only occur in the secrecy array gain because secrecy diversity order is not affected by NE(indicated by the parallel slopesof theasymptotes).

▲Figure2.Secrecy outageprobability versusγB for RS=0.1,γE=5 dB,N B=3,and N E=2.

▲Figure3.Secrecy outageprobability versusγB for RS=0.1,γE=5 dB,N A=2,and N E=2.

n Fig. 5 [25], secrecy outage probability is plotted against γ B to show the effect ofLB on secrecy. In Fig. 5, secrecy outage diversity gain is 8, regardless ofLB . Secrecy outage probability decreases asLB increases. TAS/GSC provides a greater SNR advantage than TAS/SC and provides comparable secrecy out⁃age to that of TAS/MRC. GSC is less complex than MRC but more complex than SC, so there is a cost-performance tradeoff with TAS/GSC in terms of in terms of physical layer security.In Fig. 6 [22], the probability of non-zero secrecy capacity is plotted againstγ B. For a fixedγ B, Pr [CS ＞0] increases asγ B increases. Moreover, Pr [CS ＞0] decreases asγ E increases. Non⁃zero secrecy capacity exists even when the eavesdropper's channel is statistically better than the main channel, that is,whenγ E ＞γ B

▲Figure4.Secrecy outageprobability versusγB for RS=0.1,γE=5 dB,N A=3,and N B=3.

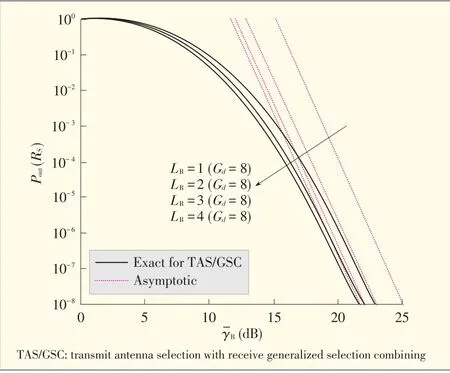
▲Figure5.Secrecy outageprobability versusγ-B for RS=1,γ-E=5 dB,N A=2,N B=4,N E=3,and L E=2.

Fig.7[25]shows TAS and TBFε-outage secrecy rates against NAforε=0.01.The TBF is the same as that in[18].Maximal-ratio transmission is used at Alice,and a single an⁃tenna is installed at Bob.In Fig.7,NB=1 for a fair compari⁃son.The secrecy outage probability of TBF with GSC at the eavesdropper is derived from[25,eq.(17)].Fig.7 shows that,for both TAS and TBF,RSmaxincreases as NAincreases.TAS Rmaxapproximates TBF Rmaxwhen N is small.Also,the rate advantage of TBF over TASincreases as NAincreases.Howev⁃er,with TBF,this advantage comes at the cost of higher feed⁃back and overhead.TBF feedback and overhead increases as NAincreases;however,TAS feedback and overhead is un⁃changed.

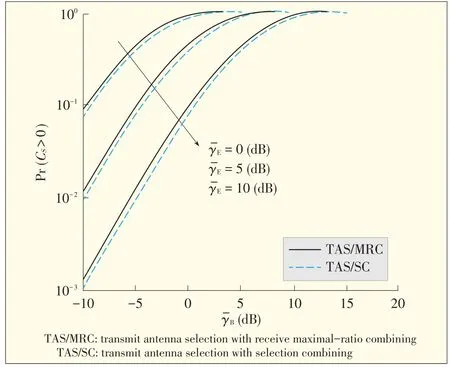
▲Figure6.Probability of nonzero secrecy capacity versusγB for N A=4,N B=3,and N E=2.

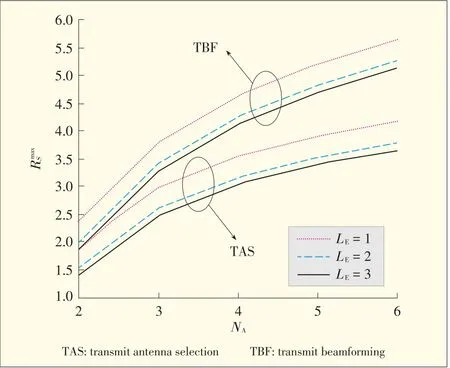
▲Figure7.ε-outagesecrecy ratebetween TASand TBFversus N A for=20 dB,N B=1,=0 dB,and N E=3.

6 Conclusion

In this paper,we have reviewed TAS,which is designed to increase physical layer security in MIMO wiretap channels.A general analytical framework has been described that allows us to accurately determine the asymptotic secrecy of TAS/MRC,TAS/SC,and TAS/GSC.The asymptotic results show that TAS/MRC,TAS/SC,and TAS/GSChave the same secrecy outage di⁃versity order.The tradeoff of TAS/GSCrelative to TAS/SCand TAS/MRC is characterized by their respective secrecy outage SNR gains.