Wireless Physical Layer Security with Imperfect Channel State Information:A Survey

Biao He,Xiangyun Zhou,and Thushara D.Abhayapala

(Research School of Engineering,the Australian National University,Australia)

Abstract Physical layer security is an emerging technique for improving wireless communication security,which is widely regard⁃ed as a complement to cryptographic technologies.To design physical layer security techniques for practical scenarios,uncertainty and imperfections in the channel knowledge need to be taken into account.This paper is a survey of recent research on physical layer security that considers imperfect channel state information(CSI)at communication nodes.We first give an overview of the main information-theoretic measures of secrecy performance with imperfect CSI.Then,we describe several signal processing enhancements in secure transmission designs.These enhancements include secure on-off transmission,beamforming with artificial noise,and secure communication assisted by relay nodes or in cognitive radio systems.Recent studies of physical layer security in large-scale decentralized wireless networks are also summa⁃rized.Finally,open problems for on-going and future research are discussed.

Keyw ordsphysical layer security;fading channels;channel uncertainty;imperfect channel state information

1 Introduction

Secure communication over wireless fading channels becomes a critical issue due to the broadcast nature of wireless networks.Traditionally,key-based cryp⁃tographic technologies[1]are used to secure the data transmission.However,the secrecy provided by cryptographic technologies is conditioned on the premise that the eavesdrop⁃pers have limited computational capability to decipher the message without the knowledge of secret keys.This premise has become controversial with the rapid development of com⁃puting devices.Physical layer security is an emerging research area that explores the possibility of achieving perfect-secrecy data transmission between legitimate network nodes,while ma⁃licious nodes eavesdropping the communication obtain zero in⁃formation[2].To achieve the secure communication over wire⁃less channels,physical layer security does not rely on the en⁃cryption,but studies the time-varying property of fading chan⁃nels,the smart design on channel codes,and the process on transmitted signals.Theinformation-theoretic foundation of se⁃cret communication was laid by Shannon[3].Wyner′s pioneer⁃ing work introduced the wiretap channel model as a basic framework for physical layer security[4],which was extended to broadcast channels with confidential messages described by Csiszár and Körner[5].These early works have led to a signifi⁃cant amount of recent research in which the fading characteris⁃tics of wireless channels has been taken into account.The ba⁃sic system model of physical layer security over wireless chan⁃nelsisshown in Fig.1.

Most works in this area rely on perfect knowledge of both the legitimate receiver and eavesdropper′s channels at the transmitter to enable secure encoding and advanced signaling.However,the assumption of perfect knowing channel state in⁃formation(CSI)is not realistic.In practical scenarios,there ex⁃ist many reasons for imperfections in the CSIat the communi⁃cation nodes.For example,

·No feedback from the eavesdroppers.When the eavesdropper is a passive entity,its CSIor even location is difficult to obtain at the legitimate transmitter.Also,if the eavesdrop⁃pers are malicious users,they will not expose their channel information tothelegitimateparty.

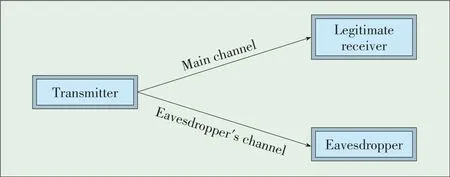
▲Figure1.Basic system model of physical layer security over wirelesschannels.

·Partial CSI feedback from the receivers.Receivers some⁃timesonly providepartial CSIfeedback tothetransmitter,e.g.,limited-rate feedback,channel direction feedback,and signal-to-noise ratio(SNR)feedback.

·Imperfect feedback linksbetween thetransmitter and receiv⁃ers.When the feedback links are not error-free or delay⁃less,a noise component is added into the feedback informa⁃tion or elsethe CSIobtained at thetransmitter isoutdated.

·Channel estimation errors at receivers.Since the estimation of fading channels generally is not error-free,the CSI ob⁃tained at thereceiver isnot perfect.

Over the past few years,increasing attention has been paid to the impact of uncertainty in the CSI on both the legitimate receiver and eavesdropper′s channels.The remainder of this paper is devoted to surveying and reviewing the literature on physical layer security with imperfect CSI1Thework on systemswith imperfect instantaneous CSIoften coversthecase of asystem with noinstantaneous CSI,sinceimperfect instantaneous CSIwith very large uncertainty naturally convertstothecaseof noinstantaneous CSI.in wireless commu⁃nications.We aim to provide a high-level overview of the cur⁃rent research on this field.In addition,this survey focuses on physical layer security research that does not involve the use of a secret key.Some work on physical layer security,e.g.,[6]-[10],investigated the secure transmission with the key that can be observed by the eavesdropper over wireless channels.

The remainder of this paper is organized as follows.In Sec⁃tion 2,we discuss research done from the information-theoret⁃ic perspective.We present the main performance metrics for secure transmissions with imperfect CSI.In Section 3,we re⁃view signal processing secrecy enhancements in the secure transmission design that takes into account the imperfect CSI.Section 4 turns to the research on secrecy with channel uncer⁃tainty in large-scale decentralized wireless.Open problems and possible future research directions are described in Sec⁃tion 5.Finally,Section 6 concludesthepaper.

2 Characterizationsof the Performance Limits

The performance limits of secure transmission systems with full CSI are often characterized by the secrecy capacity.The secrecy capacity for the degraded wiretap channel with addi⁃tive Gaussian noise(AWGN)is given by[11],

where CMand CEdenotethe Shannon capacitiesof the main(le⁃gitimate receiver′s)and eavesdropper′s channels,respectively.A positive secrecy capacity can be obtained only when the le⁃gitimate receiver′s channel is better than the eavesdropper′s channel.When fading channels are considered,the main and eavesdropper′s channels for a specific fading realization can be regarded as complex AWGN channels.The Shannon capaci⁃ties of one realization of the quasi-static fading channels are given by

whereγMandγEare the instantaneous SNRs at the legitimate receiver and eavesdropper,respectively.The instantaneous SNR at the legitimate receiver is given byγM=P｜hM｜2/σ2M,where P denotes the transmit power,hMdenotes the instanta⁃neous channel gain at the legitimate receiver,andσ2Mdenotes the receiver noise variance at the legitimate receiver.Also,the instantaneous SNRattheeavesdropper givenbyγE=P｜hE｜2/σ2E,where hEdenotes the instantaneous channel gain at the eaves⁃dropper andσ2Edenotes the receiver noise variance at the eavesdropper.Thus,the secrecy capacity for one realization of the quasi-static fading channels can be written as

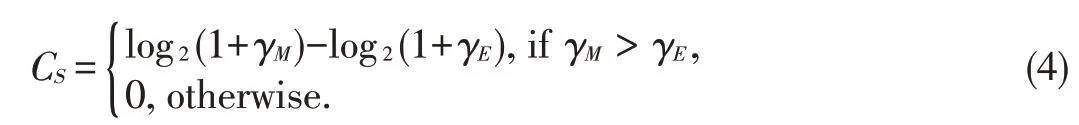
Note that,to achieve the secrecy capacity in(4),the trans⁃mitter needsperfect knowledgeof bothγMandγE.

To measure the performance of secure transmissions over fading channels with imperfect CSI,ergodic secrecy capacity and outage-based characterizations are often adopted.In the following,focusing on these two kinds of characterizations,we provide a review on the information-theoretic aspect of re⁃search in the field of physical layer security with imperfect CSI.In addition,we briefly describe the secrecy-degrees of freedom,which applies to systems with pessimistic and strong CSIassumptions.

2.1 Ergodic Secrecy Capacity

Ergodic secrecy capacity applies to delay tolerant systems in which the encoded messages are assumed to span sufficient channel realizations so that the ergodic features of the channel are captured.Ergodic secrecy capacity reveals the capacity limit under the constraint of perfect secrecy.Typical examples of delay tolerant applications are document transmission and e-mail,both of which belong in the category of non-real-time data traffic.

Gopala et al.[12]described ergodic secrecy capacity for both the case of full CSI and the case of only main channel′s CSI available at the transmitter.The secrecy capacity for one realization of the quasi-static fading channels is given in(4).Averaged over all fading realizations,the ergodic secrecy ca⁃pacity of fading channels with full CSIisgiven by

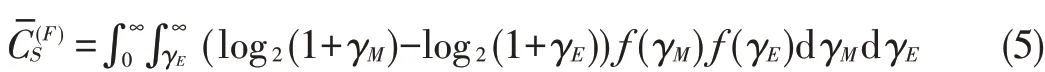
whereƒ(γM)andƒ(γE)are the distribution functions ofγMand γE,respectively.Because the transmitter has full CSI on both channels,the transmitter can make sure that the transmission occurs only whenγM＞γE.When only the channel gain of the legitimate receiver is known at the transmitter,the ergodic se⁃crecy capacity isgiven by

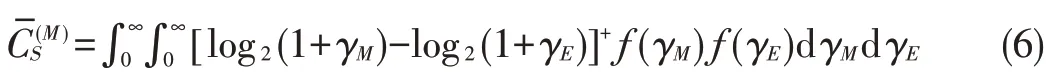
where[x]+=max{x,0}.Gopala et al.[12]also outlined a vari⁃able-rate transmission scheme to show the achievability of er⁃godic secrecy capacity with only main channel information.Duringacoherenceinterval with thereceived SNRat thelegiti⁃mate receiver,γM,the transmitter transmits codewords at a rate of log2(1+γM).This variable-rate scheme relies on the as⁃sumption of large coherence intervals and ensures that when γM＜γE,the mutual information between the source and the eavesdropper is upper-bounded by log2(1+γM).WhenγM≥γE,this mutual information is equal to log2(1+γE).Averaged over all the fading states,the achievable perfect secrecy rate is giv⁃en as(6).The secure message is hidden across different fading states.

Fig.2 compares the ergodic secrecy capacity of the network with full CSIat the transmitter and that of the network with on⁃ly main channel CSI at the transmitter.The average channel qualities are E{｜hM｜2}=E{｜hE｜2}=1,where E{·}is the expec⁃n operation.The average power constraint is denoted byE{P}.According to(5),the transmission occurs only when｜hM｜2＞｜hE｜2.Thus,the constant power lused for transmission with full CSIat thetransmitter is P=r(｜hM｜2＞｜hE｜2),where Pr(·)denotes the probabilmeasure.Note that P=0 for|hM|2≤|hE|2,and hence E{P}=On the other hand,the constant power level used for traission with only main channel CSIat thetransmitter is P=

In addition,Khisti and Wornell[13]studied the ergodic se⁃crecy capacity in multiple-input,single-output,multi⁃ple-eavesdropper(MISOME)systems.The authors developed upper and lower bounds on the ergodic secrecy capacity when there is perfect legitimate receiver′s CSI and imperfect eaves⁃dropper′s CSI.The authors also investigated the ergodic secre⁃cy capacity of fast-fading channel for both high SNR and fi⁃nitely many antennas,i.e,the number of transmitted antenna is very large.Rezki et al.[14],[15]studied the ergodic secrecy capacity for systems with imperfect CSI on both legitimate re⁃ceiver and eavesdropper′s channels at the transmitter.In[14],the authors presented a framework that characterizes the ergo⁃dic secrecy capacity of fast-fading channels when the legiti⁃mate receiver′s CSI is imperfectly known at the transmitter.In[15],the authors established upper and lower boundson the er⁃godic secrecy capacity for a single-input,single-output,sin⁃gle-eavesdropper(SISOSE)system with limited-rate feedback of thelegitimatereceiver′schannel information.

2.2 Outage-Based Characterizations

As mentioned before,the ergodic secrecy capacity applies to delay-tolerant systems which allow for the use of an ergodic version of fading channels.However,perfect secrecy cannot al⁃ways be achieved for systems with stringent delay constraints,and ergodic secrecy capacity is inappropriate to characterize the performancelimitsof such systems.On theother hand,out⁃age-based characterizations,which measure systems with probabilistic formulations,are more appropriate.

Assuming the fading is quasi-static,Parada and Blahut[16]analyzed thescenariowhereboth legitimatereceiver and eaves⁃dropper′s CSI is not available at the transmitter.The authors provided an alternative definition of outage probability.Ac⁃cording to this definition,the secure communication can be guaranteed for the fraction of time when the legitimate receiv⁃er′s channel is stronger than the eavesdropper′s channel.Bar⁃ros and Rodrigues[17]provided the first detailed characteriza⁃tion of the secrecy outage capacity where the outage probabili⁃ty,pout,is characterized by the probability that a given target rate,RS,is greater than the difference between instantaneous main channel capacity,CM,and instantaneous eavesdropper′s channel capacity,CE.The outage probability is given by

The authors also showed that fading alone guarantees that physical layer security is achievable,even when the eavesdrop⁃per has a better average SNR than the legitimate receiver.In addition,Bloch et al.[2]characterized the relationship be⁃tween the upper bound of the outage probability and the vari⁃ance of the channel estimation error on eavesdropper′s chan⁃nel.The secrecy outage behavior of a multiple-input,sin⁃gle-output,single-eavesdropper(MISOSE)fading system was studied in[18],where the authors suggested a relation between the degree of channel knowledge and the tolerable secrecy out⁃ageprobability.

In[2],[16]-[18],the outage-based formulations capture the probability of having a reliable and secure transmission.Reli⁃ability and security are not differentiated,because an outage occurs whenever the transmission is either unreliable or not perfectly secure.Zhou et al.[19]presented an alternative se⁃crecy outage formulation that directly measures the probability that a transmitted message is not perfectly secure.The alterna⁃tive secrecy outage is given by

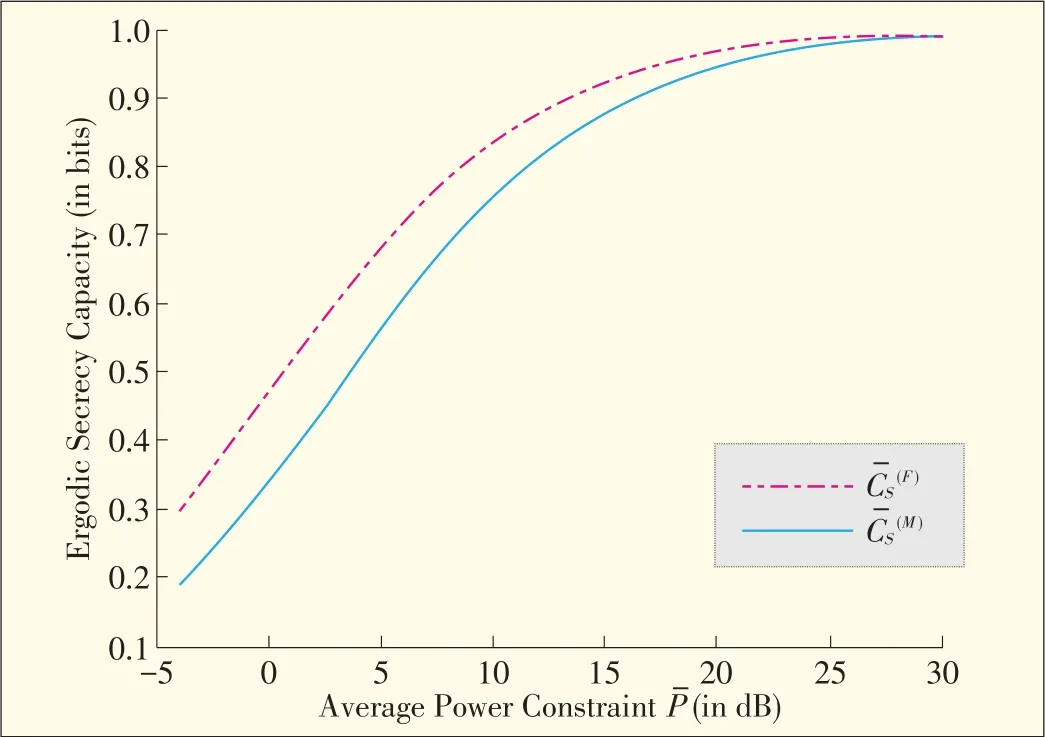
▲Figure2.Ergodic secrecy capacity versusaveragepower constraint.Theaveragechannel qualitiesare E{|h|2}=E{|h|2}=1.

where RMand RSare the rate of transmitted codeword and the rate of the confidential information in the wire-tap code,re⁃spectively.The outage probability is conditioned on a message actually being transmitted.From(8),we see that the new for⁃mulation takes into account the system design parameters,such asthe rate of transmitted codewordsand the condition un⁃der which message transmissions take place.Therefore,the al⁃ternative secrecy outage formulation is useful for for designing transmission schemesthat meet target security requirements.

Fig.3 compares the secrecy outage probability of not having a reliable and secure transmission,poutin(7),and the secrecy outage probability of not having a secure transmission,psoin(8).The average received SNRs are E{γM}=E{γE}=1.The de⁃tailed discussion on the comparison of these secrecy outage probabilitiescan befound in[19].

2.3 Secrecy Degreesof Freedom

Alongside research on ergodic secrecy capacity and out⁃age-based characterizations,another line of research,e.g.,[20]-[24],studies the performance limits of systems with im⁃perfect CSI under a pessimistic but strong assumption that al⁃lows the eavesdropper′s channel to vary arbitrarily.These work analyzed the so-called secrecy degrees of freedom(SDoF),which is the pre-log of the secrecy capacity at high SNR and reveals the asymptotic behavior of the achievable secrecy rate in ahigh-SNRregime.The SDoFisformulated as wheredenotes the average power constraint on transmitted signals.

The SDoF region for a single-user Gaussian multiple-input,multiple-output(MIMO)wiretap channel was investigated in[20].The SDoF region of a two-user Gaussian MIMO broad⁃cast channel with arbitrarily varying eavesdropper channel was found in[21].The SDoF region for a two-user Gaussian MIMO multiple access channel and a Gaussian two-way channel with arbitrarily varying eavesdropper channel were given in[22]and[23],respectively.The SDoF region for a two-user MIMO interference channel with an external eavesdropper was given in[24].In addition,there is a main limitation in this type of works,i.e,the legitimate receiver is always required to have an advantage over the eavesdropper in terms of the antenna num⁃ber in order toget positive SDoF.

3 Signal Processing Secrecy Enhancements

In this section,we present signal processing techniques for enhancing secrecy of wireless communications.Specifically,secure on-off transmissions for signal-antenna channels,beamforming with artificial noise for multi-antenna channels,and secure design techniques for relay channel and cognitive radio systems are described in the following threesubsections.

3.1 Secure On-off Transmissionsfor Single-Antenna Channels

Secure on-off transmission policy in wireless network de⁃signs generally works in the following way.The transmitter de⁃cides whether or not to transmit according to the knowledge of CSI on the legitimate receiver′s channel,eavesdropper′s chan⁃nel,or both channels(if applicable).Transmission takes place whenever the estimated instantaneous CSI fulfills the require⁃ments related to some given thresholds,e.g.,SNR thresholds.Otherwise,transmission issuspended.

Gopala et al.[12]proposed a low-complexity,on-off power allocation strategy accordingto theinstantaneous CSIon thele⁃gitimate receiver′s channel,which approaches optimal perfor⁃mance for asymptotically high average SNR.Zhou et al.b[19]designed two on-off transmission schemes,each of which guar⁃antees a certain level of security whilst maximizing the throughput.With the statistics of eavesdropper′s channel infor⁃mation,the first scheme requires CSIfeedback from the legiti⁃mate receiver to the transmitter,and the second scheme only requires 1-bit feedback.Rezki et al.[14]studied a system in which the transmitter knows imperfect legitimate receiver′s CSI and statistics of eavesdropper′s channel.The authors derived the achievable rate of fast-fading channels with a simple on-off scheme and Gaussian input.In addition,under various assumptionson the CSI,He and Zhou[25]proposed several se⁃cure on-off transmission schemes,which maximize the throughput subject to a constraint on secrecy outage probabili⁃ty.Both fixed-rate and variable-rate transmissions were pro⁃posed.The authors not only considered the imperfect CSI at the transmitter,but also studied the impact of imperfect CSIat thereceiver side.

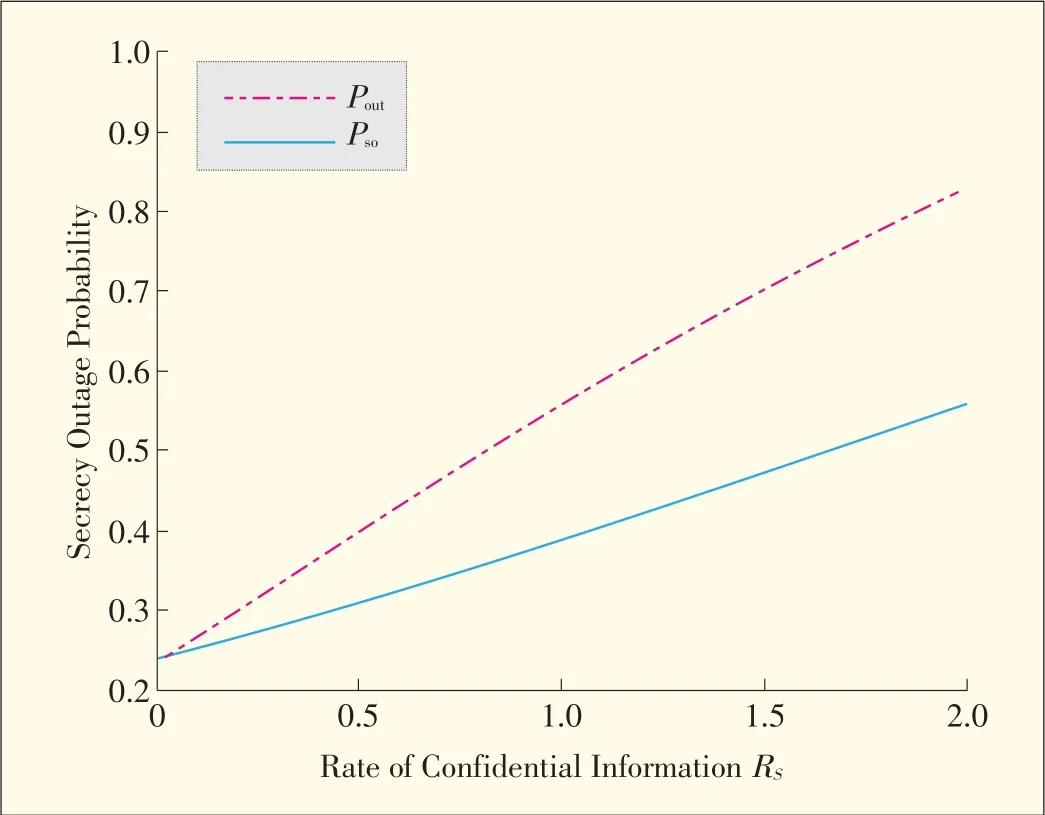
▲Figure3.Secrecy outageprobability versusrateof confidential information.Theaveragereceived SNRsare E{γ}=E{γ}=1.

3.2 Beamforming with Artificial Noisefor Multi-Antenna Channels

The work by Hero[26]is arguably the first to consider se⁃cret communication in a multi-antenna transmission system,and sparked significant efforts to this problem [27].For multi-antenna channels with imperfect CSI,beamforming with artificial noise is the one of the most widely used techniques to secure the data transmission.Negi and Goel[28],[29]are the first to propose an artificial-noise injection strategy.As well as being allocated to transmitting information signals,part of the transmission power is allocated to generating artificial noise that confuses the eavesdropper.Specifically,the produced arti⁃ficial noise lies in the null space of the legitimate receiver′s channel,and the information signal is transmitted in the range space of the legitimate receiver′s channel.This technique re⁃lies on the instantaneous CSIon the legitimate receiver′s chan⁃nel,but does not require the instantaneous CSI on the eaves⁃dropper′s channel.The legitimate receiver′s channel nulls out the artificial noise.Thus,the legitimate receiver is not affected by the noise.The basic idea of beamforming with artificial noiseispresented in Fig.4.

In the following,we discuss the work that came after Negi and Goel′sresearch,which focused on thebeamformingwith ar⁃tificial noise in various multi-antenna channel scenarios with different assumptions on the availability of CSI.We first pres⁃ent the literature considering imperfect CSI on the eavesdrop⁃per′s channel,and then discuss the work which considers the imperfect CSI on both eavesdropper and legitimate receiver′s channels.

3.2.1 Imperfect CSIon Eavesdropper′s Channel

The work of Zhou and McKay[30]studied the optimal pow⁃er allocation between the information signal and artificial noise in systems with both non-colluding and colluding eavesdrop⁃pers.The authors found that,in the case of non-colluding eavesdroppers,the equal power allocation results in nearly the same secrecy rate as if power are optimally allocated.In the case of colluding eavesdroppers,they found that more power should be allocated to transmitting artificial noise as the num⁃ber of eavesdroppers increases.In[31],Zhang et al.investigat⁃ed the design of artificial-noise-aided secure multi-antenna transmission in slow-fading channels.The authors provided throughput-maximizing design solutions that include the the optimal rate parameters of the wiretap code and the wise pow⁃er-allocation strategy.Huang and Swindlehurst[32]obtained robust transmit covariance matrices on worst-case secrecy rate maximization under both individual and global power con⁃straints.They investigated both cases of direct transmission and cooperative jamming with a helper.In addition,Gerbracht et al.[18]characterized optimal single-stream beamforming with the use of artificial noise to minimize the outage probabili⁃ty.They pointed out that the solution convergesto maximumra⁃tio transmission(MRT)for the case of no CSIto the eavesdrop⁃per,and the optimal beamforming vector converges to the gen⁃eralized eigenvector solution with the growing level of CSI.Lin et al.[33]showed that the artificial noise selected in[29]is suboptimal.According to their study,the eigenvectors of the optimal covariance matrices of both information signals and generalized artificial noise are equal to the right singular vec⁃torsof the legitimate receiver′s channel.Also,the power of arti⁃ficial noise should be allocated uniformly over the eigenvec⁃tors.Therigorousproofsfor thesefactswerealsoprovided.

In[18],[29]-[33],although the instantaneous CSI on the eavesdropper′s channel is not required,the transmitter still needs the statistics of eavesdropper′s channel.For the case where no CSIon the eavesdropper′s channel(including the sta⁃tistics)is known at the transmitter,Swindlehurst and Mukher⁃jee[34],[35]proposed a modified water-filling algorithm which balances the required transmit power with the number of spatial dimensions available for jamming the eavesdropper.As described in the modified water-filling algorithm,the transmit⁃ter first allocates enough power to meet a target performance criterion,e.g.,SNR or rate,at the receiver,and then uses the remaining power to broadcast artificial noise.In[36],the au⁃thors also applied the similar algorithm to investigate the mul⁃tiuser downlink channels in.

3.2.2 Imperfect CSIon Both Eavesdropper and Legitimate Receiver′s Channels

▲Figure4.An illustration of beamforming with artificial noise.

The imperfect CSIon the legitimate receiver′s channel at the transmitter mainly incurs two problems.First,without knowing the actual instantaneous CSI on the legitimate receiver′s chan⁃nel,the transmitter cannot make sure that the data transmis⁃sion rate is not larger than the legitimate receiver′s channel ca⁃pacity.Then,a transmitted packet is unable to be decoded by the receiver,i.e.,the packet is corrupted,whenever the data transmission rate exceeds the legitimate receiver′s channel ca⁃pacity.Second,when the legitimate receiver′s instantaneous CSIisimperfect,theartificial noiseleaksintothelegitimatere⁃ceiver′s channel,because the beamforming with artificial noise is designed according to the estimated instantaneous CSIrath⁃er than the actual instantaneous CSI.Therefore,the artificial noise interferes with the desired user,although it is intended to only confuse the eavesdropper.Naturally,the techniques ap⁃plying to systems with perfect CSI on the legitimate receiver′s channel becomenot optimal.

Taylor et al.[37]presented the impact of the legitimate re⁃ceiver′s channel estimation error on the performance of an ei⁃genvector-based jamming technique.Their research showed that the ergodic secrecy rate provided by the jamming tech⁃nique decreases rapidly as the channel estimation error in⁃creases.Mukherjee and Swindlehurst[38]also pointed out that the security provided by beamforming approaches is quite sen⁃sitive to imprecise channel estimates.The authors proposed a robust beamforming scheme for MIMOsecure transmission sys⁃tems with imperfect CSI of the legitimate receiver.Pei et al.[39]addressed a stochastic time-varying CSIuncertainty mod⁃el with uplink-downlink reciprocity.Using this model,they proposed a new iterative algorithm to secure the transmission.The algorithm is robust against CSI errors.The authors of[30]investigated the effects of imperfect CSIon optimal power allo⁃cation and critical SNR for secure communications.They found that allocating power to the artificial noise for confusing the eavesdropper is better than increasing the signal strength for the legitimate receiver as the channel estimation error in⁃creases.Adapting the secrecy beamforming scheme,Liu et al.[40]investigated the joint design of training and data transmis⁃sion signals for wiretap channels.The ergodic secrecy rate for systems with imperfect channel estimations at both the legiti⁃mate receiver and the eavesdropper was derived.The secrecy rate is difficult to be calculated,since the channel estimation errors cause non-Gaussianity of equivalent noise.The authors solved thisproblemby analyzing a large number of transmit an⁃tennas.Based on the achievable ergodic secrecy rate,the opti⁃mal tradeoff between the power used for training and data sig⁃nals can be found.Furthermore,advocating the joint optimiza⁃tion of the transmit weights and artificial noise spatial distribu⁃tion from a quality-of-service(QoS)-based perspective,Liao et al.[41]proposed a secret-transmit beamforming approach in accordance with the imperfect CSIon both the legitimate re⁃ceiver and eavesdropper′s channels.In[42],Ng et al.ad⁃dressed a resource-allocation and scheduling optimization problem for orthogonal frequency division multiple access(OFDMA)networks.The optimization problem takes into ac⁃count artificial noise generation and the effects of imperfect CSIin slow fading.The authors proposed a resource allocation algorithm that accounts for secrecy outage,channel outage,and the potentially detrimental effect of artificial noise genera⁃tion.Considering the systems with partial CSIfeedback,Lin et al.[43]investigated the scenario where only quantized channel direction information(CDI)of the legitimate receiver′s channel is available at the transmitter.Given the transmission power and a fixed number of feedback bits,the authors derived the optimal power allocation between the information signal and the artificial noise sothat the secrecy rateis maximized.

In addition,it is necessary to mention that some works(e.g.,[33],[44]-[46])also studied the approaches to provide physi⁃cal layer security for multi-antenna systems with imperfect CSI,but they did not rely on the use of artificial noise.Li and Petropulu[44]solved optimal input covariance that maximizes the ergodic secrecy rate subject to a power constraint in a MISOSE system with imperfect CSIon eavesdropper′s channel.Li and Ma[45]formulated a transmit-covariance optimization problem for secrecy-rate maximization(SRM)of MISOME sys⁃temswith imperfect CSIon both main and eavesdropper′schan⁃nels.The authors of[33]analyzed systems with only statistics of the main and eavesdropper′s channels at the transmitter.The authors showed that the secure beamforming can still achieve the secrecy capacity in such a scenario,and they proposed the optimal channel input covariance matrix,which fully character⁃izesthesecrecy capacity.Theauthorsalsopointed out that arti⁃ficial noise is not necessary in thiscase.Geraci et al.[46]stud⁃ied the secrecy sum-rates achievable by regularized channel inversion(RCI)precoding in MISOsystemswith imperfect CSI.

3.3 Secure Designsfor Relay Channelsand Cognitive Radio Systems

Secure communication assisted by relay nodes is often re⁃garded as a natural extension of secure transmission in multi-antenna networks.Physical layer security can be provid⁃ed by careful signaling at different relays in the system.A vir⁃tual beam towards the legitimate receiver can be built by the collaboratively work among relay nodes,which issimilar to se⁃cure transmission in multi-antenna systems.However,unlike the multiple-antenna transmission,the transmitter cannot di⁃rectly control the relays.Goel and Negi[29]described a 2-phase protocol for the network of single-antenna wiretap channel with serval relays.This protocol was designed to ob⁃tain coordination in transmittingartificial noise between the re⁃lays.In the first phase,the transmitter and the legitimate re⁃ceiver both transmit independent artificial noise signals to the relays.Different linear combinationsof these two signals are re⁃ceived by the relays and the eavesdropper.In the second phase,the relays replay a weighted version of the received sig⁃nal,using a publicly available sequence of weights.Mean⁃while,the transmitter transmits the confidential information,along with a weighted version of the artificial noise transmitted in the first stage.With the knowledge of the artificial noise component due to the legitimate receiver,the legitimate receiv⁃er is able to cancel off the artificial noise and get the confiden⁃tial information.Assuming global full CSI at every node,the authors in[47]provided a detailed analysis on secure commu⁃nications of one source-destination pair with the help of multi⁃ple cooperating relays in the presence of one or more eaves⁃droppers.Thisanalysiscovered decode-and-forward(DF),am⁃plify-and-forward(AF),and cooperative jamming(CJ)three different cooperative schemes.

To explore the effects of imperfect CSI in relay systems,re⁃searchers often consider the uncertainty of CSI on three kinds of links:relay-destination,relay-eavesdropper,and source-re⁃lay.The authors of[48]investigated the effect of imperfect CSI on the relay-eavesdropper channels.They proposed a DF re⁃laying protocols for secure communication,which maximizes the lower bound on the ergodic secrecy capacity under a total relay transmission power constraint.Considering the imperfect CSIon the channels from relay to destination and from relay to eavesdropper,Zhang and Gursoy[49]provided optimization frameworks for the robust DF-based relay beamforming de⁃sign.Furthermore,Vishwakarma and Chockalingam[50]com⁃puted the worst-case secrecy rate when there are imperfec⁃tions in the CSI on all the links,i.e.,relay-destination links,relay-eavesdropper links,and source-relay links.

Cognitive radio(CR)hasbeen widely recognized asan effec⁃tive technology to improve the utilization of wireless spectrum by allowing secondary users to coexist with primary users and access the spectrum of the prime system.In CR systems with secrecy message broadcasted in the primary links,the signals of secondary links for their users can also serve as the artificial noise for the secureprimary link.In order toconfusetheeaves⁃dropper overhearing the primary links,the secondary system operates similar to that of the helper nodes,but simultaneously serves their own receivers.The papers that study the imperfect CSI in such cognitive radio systems can be found in[51]and references within.The authors of[51]explored MISO CR sys⁃tems where the secondary system secures the primary commu⁃nication in return for permission to use the spectrum.On the other hand,when the secondary user transmitter sends confi⁃dential information to a secondary user receiver on the same frequency band as that of a primary user,the requirement of not interfering the primary user is often treated as a power con⁃straint on the transmitted signals in the secondary system.As⁃suming all CSI is imperfect known,Pei et.al[52]explored an optimal secondary user transmitter design,which maximizes the secure transmission rate of the secondary link while avoid⁃ing harmful interference to primary users.The authors pro⁃posed two approaches to solving this challenging optimization problem,which isnon-convex and semi-infinite.

4 Secrecy in Large-Scale Decentralized Wireless Networks

In the last section,we summarized the research results on physical layer security enhancements for systems consisting of a small number of nodes.We now turn our attention to another very important class of wireless networks:large-scale decen⁃tralized wireless networks.In such networks,the CSI of eaves⁃droppers is rarely available at legitimate users.Even the loca⁃tions of eavesdroppers may not be known.The lack of eaves⁃dropper′s information makes communication security a chal⁃lenging problem.Apart from that,the decentralized nature of the network rules out any global optimization approach for se⁃crecy enhancements.Pioneering works on physical layer secu⁃rity in large-scale decentralized wireless networks focused on the connectivity analysis.Specifically,the notion of secrecy graph was introduced in[53]and further developed in[54]to include fading channels.Various secure connectivity improve⁃ments were discussed in[55],[56],including multi-antenna sectoring and beamforming.The connectivity in the presence of thelocation uncertainty of eavesdropperswasstudied in[57].

Building on the connectivity analysis of the secrecy graph,the secrecy capacity scaling was analyzed in[58]-[62].Specifi⁃cally,the studies in[58],[59]showed that the secrecy require⁃ment does not reduce the capacity scaling of the network,i.e.,the capacity scaling law is the same for both insecure message transmission and secure message transmission.Of course,achieving such an optimal scaling law under the secrecy con⁃straint requires very different transmission and access proto⁃cols.For example,when eavesdroppers′locations are unknown,various secrecy enhancements such as cooperative jamming and multi-path transmission in conjunction with network cod⁃ingmay berequired[61],[62].

Although the scaling law results may provide insights into the asymptotic secrecy throughput performance of large-scale networks,a finer view of throughput is necessary to better un⁃derstand the impact of key system parameters and transmis⁃sion protocols,since most of design choices affect the actual(non-asymptotic)throughput but not the scaling behaviors.To this end,a new performance metric named secrecy transmis⁃sion capacity was developed in[63],[64]to capture the area spectral efficiency of secure transmission.The formulation of such a metric was based on the outage approach in[19]which accommodates a practical scenario where the CSIof the eaves⁃droppersisunknown tothelegitimatenodes.

5 Open Problemsand Discussions

Despite the increasing attention paid to the effect of imper⁃fect CSIon physical layer security,research on this area is still at an early stage.In this section,we discuss some open prob⁃lems in the research area of physical layer security with imper⁃fect CSI.

5.1 Imperfect Channel Estimation at Receivers

For research on physical layer security considering imper⁃fect CSI,most of the existing works investigate the impact of imperfect CSIat the transmitter but assume perfect channel es⁃timation at receivers.Only a few works,e.g.,[25],[30],[40],paid attention to the imperfect channel estimation at receivers.Clearly,the assumption of perfect channel estimation at the re⁃ceiver is not very practical,since the estimation of fading chan⁃nels generally is not error-free.In principle,the channel esti⁃mation error exists at both the legitimate receiver and the eavesdropper.Assuming perfect estimation at the eavesdrop⁃per is more reasonable from the secure transmission design point of view,since it is often difficult or impossible for the transmitter to know the accuracy of the eavesdropper′s chan⁃nel estimate.Nevertheless,in scenarios where the eavesdrop⁃per is just an ordinary network user whose performance and other information can be tracked by the transmitter,e.g.,[13],[65],[66],the consideration of imperfect channel estimation at the eavesdropper becomesrelevant.

5.2 Imperfect Knowledgeof Eavesdroppers′Locations

With few exceptions,almost all the existing research on physical layer security assumed that the eavesdropper′s loca⁃tion is perfectly known.The validity of such an assumption strongly depends on the application under investigation.For example,when the eavesdropper is a passive entity without transmission,its location is very hard to obtain.Also,in large-scale complex networks,it is very difficult to determine eavesdroppers′locationsdue to the random deployments or mo⁃bility of nodes.Therefore,it is an interesting research direction to consider the secrecy in networks with imperfect or no knowl⁃edge of the eavesdropper′slocation at the transmitter.

6 Conclusions

In thispaper,wehave reviewed theresearch on physical lay⁃er security with practical assumptions on fading channel infor⁃mation.For the characterizations of performance limits,we de⁃scribed ergodic secrecy capacity suitable for delay tolerant sys⁃tems,outage-based characterizations for systems with strin⁃gent delay constraints,and secrecy degrees of freedom.Also,we surveyed signal processing secrecy enhancements proposed for different transmission scenarios,i.e.,secure on-off trans⁃mission for signal-antenna channels,beamforming with artifi⁃cial noise for multi-antenna channels,and other signaling de⁃signs for relay channels or cognitive radio systems.In addition,recent findings on secrecy in large-scale decentralized wire⁃less networks were reviewed.Future research directions on physical layer security with imperfect CSI include the imper⁃fect channel estimation at receiver sides and the imperfect knowledgeof eavesdroppers′locations.