Two-Way Cooperative Quantum Communication with Partial Entanglement Analysis

Yunkai Deng,Zhujun Gao,and Ying Guo

(Central South University,Changsha 410083,China)

Abstract In this paper,we describe an improved cooperative two-way quantum communication scheme that works in a for⁃ward-and-backward fashion.In thisscheme,partial entanglement analysis based on five-qubit entangled Brown stateal⁃lows for the simultaneous exchange of arbitrary unknown states between Alice and Bob(with the help of trusted Charlie).Security is guaranteed because opposing unknown states are transmitted by performing the suitable recovery operations in a deterministic way or,in the case of irregularities,no results are generated.The current two-way quantum communi⁃cation scheme can also be extended to transmit arbitrary unknown states.This is done in a probabilistic way by using two-way quantumteleportation based on thegeneralized Brown-likestate.

Keyw ords quantumteleportation;two-way communication;brown state;bell states;entanglement

1 Introduction

E ntanglement has been widely applied in quantum information theory and quantum computation[1].An elegant application of entanglement is quantum teleportation(QT)[2],[3],in which an arbitrary un⁃known state is transmitted without distributing the quantum carrier itself.QT was first proposed by C.H.Bennett et al.in 1993.Since then,QThas been theoretically and experimental⁃ly investigated[4].Several schemes with different entangle⁃ment states have been reported.These states include Bell states[5]-[7],Greenberger-Horne-Zeiling(GHZ)states[8],and W states[9],[10].Two-qubit entanglement states can be transmitted via quantum teleportation based on four-qubit en⁃tanglement states[11]-[13].All QT schemes allow one-way,point-to-point transmission of single-qubit or multi-qubit en⁃tanglement states.

In practical applications,problems arise when two partici⁃pants(Alice and Bob)exchange unknown states in a small quantumnetwork.To solve thisproblem,Mishraet al.[14]pro⁃pose a two-way quantum communication scheme in which un⁃known single-qubit states can be exchanged.This exchange is based on the six-qubit entanglement state established between Alice and Bob(with the help of a third party,Charlie).Without Charlie,Alice and Bob could not recover the required states in a deterministic way because they do not know which channel will beestablished between them.

Recently,much research has been done on the multi-qubit entanglement state.In[15],the Brown state is described.This five-qubit maximally entangled state is achieved by using a numerical optimization procedure.Because it is highly entan⁃gled,this state can be used for QT[16],quantum secret shar⁃ing,superdense coding,secure communication[17],and infor⁃mation splitting[18].In[19],Sreraman et al.[19]proposed a one-way QT for transmitting unknown states based on the Brown state.

In a quantum computation network,information may be si⁃multaneously transmitted from Alice to Bob and from Bob to Alice.Consequently,two one-way QT schemes(one from Al⁃ice to Bob and one from Bob to Alice)may be switched on.However,a network becomes insecure or dishonest when Bob achieves Alice's unknown states but fails to send his Bell state measurements(BSMs)to Alice.Alice needs to recover Bob's unknown states at the same time Bob receives Alice's unknown because QTneeds the BSM results from sender to re⁃ceiver to recover unknown states.To solve this problem,QT must simultaneously transmit Alice's unknown states to Bob and Bob's unknown states to Alice.Also,QT must either ex⁃change unknown states or,in the case of irregularities,gener⁃ate no results.In this paper,we describe a two-way QT scheme in which partial entanglement analysis is performed.This scheme makes use of two local BSMs that are based on the Brown staterather than the Bell statesusually used in stan⁃dard QTschemes.

In section 2,we describe an improved cooperative two-way QT scheme that uses the help of a trusted third party,Charlie.We analyze this scheme using partial entanglement analysis based on the Brown state.In section 3,we propose a general two-way QTscheme for transmitting unknown states backward and forward.This transmission occurs in a probabilistic way,and the unknown states are assumed to be Brown-like states.Section 4 concludesthepaper.

2 Cooperative Two-Way QT Based on Brown States

Alice,Bob and Charlie prepare a five-qubit entanglement Brown state jBri12345 as the information carrier in a small quantum network.The subscript pairs 1 and 2,and 4 and 5 re⁃fer to the modes entangled with Alice and Bob,respectively.The subscript 3 refersto the mode entangled with Charlie.This modeisgiven by

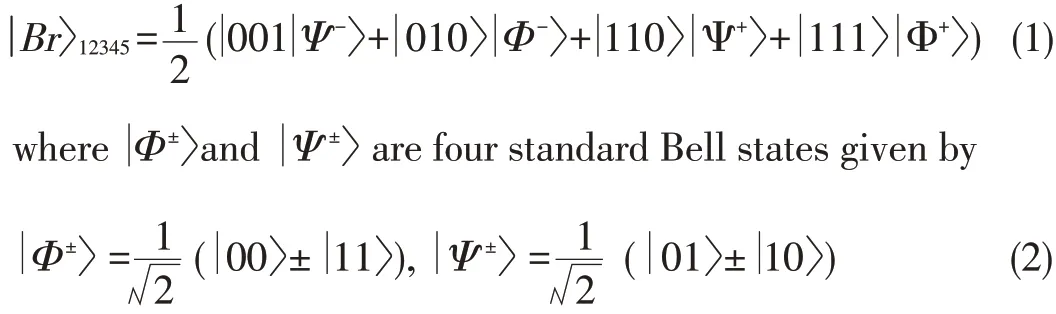
Suppose Alice sends an arbitrary unknown state in mode 0,i.e.︳φɑ〉0=α︳0〉+β︳1〉,to Bob.At the same time,Bob sends another arbitrary unknown state in mode 6,i.e.︳φb〉6=γ︳0〉+δ︳1〉,to Alice.Alice and Bob both obtain the required states or,if there is a discrepancy,do not obtain the required states.Here,the coefficients are real and satisfy the two constraints︳α〉2+︳β〉2=1 and︳γ〉2+︳δ〉2=1.The direct-product state is given as

Therefore,thecombined quantumsystemisgiven by

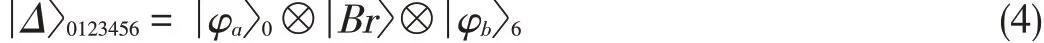
which can berewritten as

If Alice and Bob want to exchange unknown states,a secure,cooperative two-way communication scheme can be used.This scheme is implemented with the help of Charlie via two-hop QTbased on the Brown state(Fig.1).

▲Figure1.Cooperativetwo-way QT schemebased on the Brawn state.

First,Alice measures the Bell states of the photons in modes 0 and 1.At the same time,Bob measures the Bell states of the photons in modes 5 and 6.Both Alice and Bob convey their BSMs MA,MB∈{00,01,10,11}to the trusted Charlie.These BSMs are sent through the classic channels.The yielded state︳Ω〉234is achieved in modes{2,3,4}(Table 1).Then,Charlie calculates Cm=MA⊗MB=MA+MBmod 2.After that,he uses the von Neumann measurement(VNM)on the photon in mode 3,with{︳0〉,︳1〉}as the basis of this measurement.The result of the VNMconformsto MC∈{00,01},which means that MC=00/01.This corresponds to the VNM︳0〉/︳1〉.Then,Charlie cal⁃culates Dm,given by

Finally,Charlie broadcasts Dmto Alice and Bob through the classic channels.

Alice and Bob obtain MBand MA,respectively,when they decode MCfrom the received Dm.If Dm∈{00,01},then Alice obtains MC=00;otherwise,she obtains MC=01.Alice decrypts Bob's MBaccording to her own MA,which is derived from Cm.Similarly,Bob securely obtains Charlie's MCand Alice's MAfrom Dm.Finally,Alice and Bob recover the opposite unknown states︳φb〉and︳φɑ〉,respectively,after performing suitable re⁃covery operationsin modes2 and 4(Table2).

If Alice and Bob's BSMs are both︳Φ+〉,i.e.MA=MB=00,and if Charlie's VNM is︳0〉,i.e.MC=00,then the resulting state in modes 2 and 4 is

▼Table 1.Relationship between Alice's BSM and the photons in modes 0 and 1,relation⁃ships between Bob's BSM and the photons in modes 5 and 6,and the entanglement states yielded in modes{2;3;4}

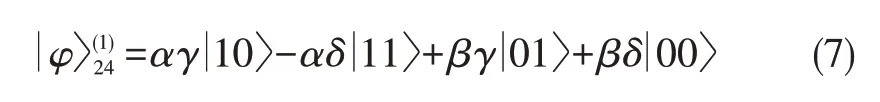
To achieve the unknown direct-product state in modes 2 and 4,and expressed in(3),Alice and Bob perform the controlled-phase operation Z in modes2 and 4,respectively,and obtain thestate

Then,Alice applies the unitary operationσxin mode2.Thisresultsin

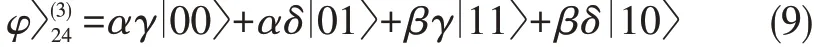
Subsequently,Alice and Bob perform the con⁃trolled-NOT operation,C(2,4),on the photons in modes 2 and 4,where mode 2 is the control qubit,and mode 4 is the target qubit.Finally,Alice and Bob obtain thedirect-product state,given by

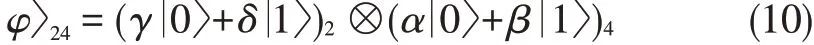
From(10),Alice can determine Bob's un⁃known state︳φb〉2in mode 2,and Bob can deter⁃mine Alice's unknown state︳φ〉in mode 4 by disentangling[1].

The controlled-phase operation performed in modes 2 and 4,is denoted Z,i.e.,Z 00〉=00〉,Z 01〉=01〉,Z 10〉=10〉,Z 11〉=-11〉.An identity operation is denoted I,and Pauli op⁃erations are denotedσzand σx.The con⁃trolled-NOTgate,denoted C(2,4),designates the control qubit in mode 2 and target qubit in mode 4.For simplicity,the normalization of the result⁃ing states is omitted.

The operations performed by Alice and Bob to exchange unknown states are depend entirely on MCof Charlie.To improve the security of the two-way QT,MA,MBand MCneed to be encrypt⁃ed by Charlie before being broadcast to Alice and Bob.Without the help of Charlie,Alice and Bob cannot exchange their unknown states.Fur⁃thermore,if either Alice or Bob fails to convey MAor MB,then Charliewill break off communica⁃tion without transmitting any information to Bob or Alice.In this scenario,we designate the se⁃cure two-way QT via the partial entanglement analysis in for⁃ward-and-backward quantumchannels.

▼Table 2.Recovery operations U 24=U 2⊗U 4 performed in modes 2 and 4 and based on Aliceand Bob's BSMs,respectively

3 Extended Cooperative Two-Way QT with the Brown-Like State

Here,weextend thetwo-way QTscheme.Thisschemeisex⁃tended in order so that unknown states,based on entangled Brown-like states established between Alice,Bob,and Char⁃lie,can be exchanged.Alice and Bob's unknown states can be represented as the direct-product state in(3).However,the f i ve-qubit entanglement state prepared as a quantum channel for QT is not maximally entangled.This is called the Brown-likestate︳ϖ〉12345and isgiven by

where the photons in modes 1 and 2,and 4 and 5 are kept by Alice and Bob,respectively.The photon in mode 3 is kept by the trusted Charlie.The coefficients are real and satisfy the constraintɑ2+b2+c2+d2=1.

Before designating the extended two-way QT scheme,Alice and Bob prepare an unknown state︳φɑ〉0in mode 0 and an un⁃known state︳φb〉6in mode 6.The f ive-qubit entanglement stateϖneeds to be established between Alice,Bob and Char⁃liein advance.Then,the whole quantum system becomes

Two-way communication in the extended system flows in a similar way to that in the previous system.Alice takes a BSM in modes 0 and 1,and this measurement is denoted MA′.At the same time,Bob takes a BSM in modes 5 and 6,and this mea⁃surement is denoted MB′.Alice and Bob both convey their BSMs to Charlie,who takes a VNM in mode 3.The basis of this measurement is{0〉,1〉},and the measurement is denot⁃ed MC′(from Cm=MA′⊗MB′).After that,Charlie broadcasts Dm=Cm⊗MC′to Alice and Bob through the classic channels.Bob decrypts MA′using the received Dmand his own MB′.Simi⁃larly,Alice obtains MB′by using the received Dmand her own MA′.Finally,Bob and Alice exchange unknown states by per⁃formingthesuitablerecovery operations.

Without a lossof generality,we consider a case in which two pairs of photons in modes 0 and 1,and 5 and 6 have collapsed into︳Φ+〉,and the VNM of Charlie is MC′=00.According to the previously mentioned process,the resulting state in modes 2 and 4 is

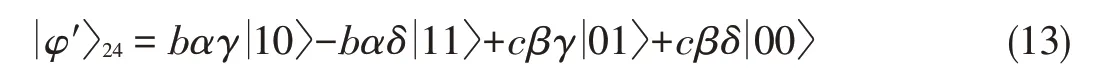
After applying the controlled phase gate Z in modes 2 and 4,Bob preparesan ancillary qubit︳0〉4′in mode 4′.Then,he per⁃forms the entangling operation C(2,4′)in modes 2 and 4′,and obtains

A state discrimination measurement can be taken to distin⁃guish b 1〉+c 0〉and b 1〉-c 0〉in mode4′[1].If thismeasure⁃ment is b 1〉+c 0〉,the yielded state in modes 2 and 4 is given by

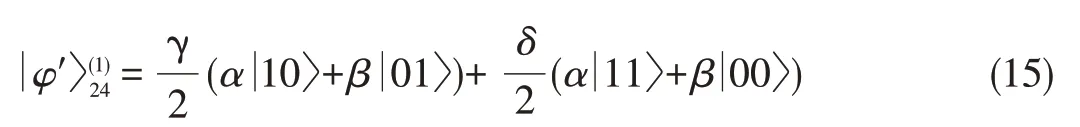
Otherwise,theyielded stateisgiven by

To enhance the security of two-way QT,Alice and Bob need to sample a large number of Brown states and compare their measurements,which are based on the entanglement of the states in the eavesdropper-detection phase.As in[20],if Eve uses an intercept-resend attack to eavesdrop on the entangled channels,she may fail to resend the intercepted state.This will be detected by the legal participants in the communication[21].Similarly,the entangled channels established between Al⁃ice,Bob and Charlie should be made much secure by using known eavesdropper detection approaches.Effective eaves⁃dropper attacks include intercept-resend[21];entanglement swapping[22];teleportation[23];dense coding[24];channel loss[25],denial-of-service(DoS)[26],[27];correlation-ex⁃tract ability[28];and Trojan horse[29],[30].These attacks need to be understood to design secure two-way QT using par⁃tial entanglement analysis in imperfect channels.In addition,authenticating[31]and signing[32]-[36]a message can se⁃cureit fromillegitimateeavesdropper.

4 Conclusion

In this paper,we have investigated an improved cooperative two-way QT scheme that makes use of partial entanglement analysis of Brown or Brown-like states.We have described how to transfer arbitrary unknown states in a secure and coop⁃erative manner.Such transference involvesencryption by trust⁃ed Charlie and combining BSM and VNM with suitable local operations.This is an alternative was of transmitting unknown states with the help of Charlie in forward-and-backward chan⁃nels.Encryption is critical in quantum repeaters to secure a quantumcomputation network.

Acknowledgements

This work was supported by the National Natural Science Foundation of China(60902044,61172184),the New Century Excellent Talents in University(NCET-11-0510),and partly by the World Class University R32-2010-000-20014-0 NRF,and Fundamental Research 2010-0020942 NRF,Korea.