Location Verification Systemsin Emerging Wireless Networks

Shihao Yan and Robert Malaney

(School of Electrical Engineeringand Telecommunications,UNSW,Sydney 2052,Australia)

Abstract As location-based techniques and applications have become ubiquitous in emerging wireless networks,the verification of location information has become more important.In recent years,there has been an explosion of activity related to lo⁃cation-verification techniques in wireless networks.In particular,there has been a specific focus on intelligent transport systems because of the mission-critical nature of vehicle location verification.In this paper,we review recent research on wireless location verification related to vehicular networks.We focus on location verification systems that rely on for⁃mal mathematical classification frameworks and show how many systems are either partially or fully encompassed by such frameworks.

Keyw ordslocation verification;wirelessnetworks;likelihood ratiotest;decision rule This work is supported by the University of New South Wales and the Australian Research Council under grant No.DP120102607.

1 Introduction

A s location-based techniques and services have be⁃come ubiquitous in emerging wireless networks,the authentication of location information has at⁃tracted considerable research interest[1]-[12].In early wireless positioning systems,accuracy and performance were of utmost importance,and authenticating location infor⁃mation was relegated to a secondary concern.This is now changing.Many current mainstream wireless positioning sys⁃tems,such as now-ubiquitous Wi-Fi positioning systems,are highly vulnerable to location-spoofing attacks because of their openness and wide public availability[13],[14].In many con⁃figurations,wireless network positioning systems are cli⁃ent-based,which means that only the client(the device whose location is to be verified)can directly obtain its location[15],[16].The wider communications network can only obtain the client's position by requesting the client to report its location.However,the client can easily spoof or falsify its location.In other configurations,systems that attempt to directly locate a client by using signal metrics,such as received signal strength(RSS)measurements,are vulnerable to manipulation of the sig⁃nal metric by the client prior to transmission[17]-[20].In this paper,we review works that attempt to formalize loca⁃tion-spoofing.We focus on location verification and assume that the location of the client is the true location and is either publicly announced by the client or a priori publicly known.We refer to this announced or known location as the claimed location.The verification systems we discuss are instructed to use all available signal metrics to classify the client according to whether it is at the claimed location or not[21]-[54].Loca⁃tion verification(or authentication)defined in this way results in a mathematical problem(and outcome)that is different to more common location acquisition problems[15]-[20].Loca⁃tion verification is important because spoofed location informa⁃tion can adversely affect a variety of network functions[2],[4],[5],[8],[55]-[62].For example,in generic wireless networks,spoofed location information can lead to dramatically reduced packet delivery in geographic routing protocols[55],[56].The performance of location-based access control can also be markedly reduced when locations are spoofed [60]-[62].Wi-Fi,cellular,and GPS position information in the E911 framework can be easily spoofed by clients in order to mali⁃ciously attract emergency services to false locations[47].How⁃ever,the adverse effects of location spoofing are arguably even more severe in vehicular ad hoc networks(VANETs)[2],[4],[5],[8].

In VANETs,location spoofing can cause life-threatening traffic accidents.Less critically,a malicious vehicle might spoof its location in order to seriously disrupt other drivers[2],[4],[5]or to selfishly enhance its own functionality within the network[35],[44].Authenticating position information within VANETs is the focus of the rest of this paper.We focus on ex⁃ploiting the physical properties of wireless communication channels to verify a location.Such an approach eliminates(or at least drastically reduces)any dependency on complex high⁃er-layer secrecy techniques,such as encryption or crypto⁃graphic key management.Using the properties of the wireless communication channels also allows us to more formally exam⁃ine the optimal performance expectations for a location verifi⁃cation system(LVS).

In section 2,we describe a generic formal LVSand associat⁃ed performance evaluation criteria.In section 3,we apply our generic LVSin an emerging VANET scenario.In section 4,we discuss other location verification systems that are not targeted at VANET scenarios but can be adapted to them.In section 5,we draw some conclusions and discuss future research direc⁃tions.

2 Generic Location Verification System

2.1 Binary Decision Rulefor an LVS

Location verification is different from locating a user in a wireless network[49].A key difference between an LVSand a positioning system is that the output of an LVSis usually a bi⁃nary decision(yes/no)whereas the output of a positioning sys⁃tem is an estimated user location.Fig.1 shows a generic LVS.Theclaimed location isan LVSinput provided by theclient be⁃ingverified(theprover).

The observations of the location verifiers are also inputs to the LVS.The LVSaims to verify a prover's claimed location by comparing these inputs and systematically checking wheth⁃er all inputs are compatible.If they are compatible,a yes deci⁃sion isreturned by the LVS.If they areincompatible,anodeci⁃sion is returned by the LVS.Because of these binary outputs,location verification can be modeled asa binary decision-theo⁃ry problem.Thus,a decision rule is embedded in an LVSand can be written as

where T is the test statistic,λis the threshold corresponding to T,and D0and D1are the binary decisions that infer whether the prover is legitimate or malicious,respectively.The test sta⁃tistic T is derived from the LVSinputs,the form of which var⁃iesaccordingtolocation verification algorithms.

In an LVSframework,we also have to consider noise(for ex⁃ample,noise in the location acquisition problem results in loca⁃tion error).Noise is usually encapsulated within the classifier logic(i.e.implicit probability distributions)of the LVS.In addi⁃tion,if the claimed position changes to a claimed area(e.g.a room),the system's implicit probability distributions are al⁃tered accordingly.

2.2 ROCsfor an LVS

From a statistical decision-theory perspective,an LVScan be modeled as a decision problem(Fig.2).In Fig.2,X is the input of an LVS,and the two realizations are H0and H1.Here,H0represents the case where the prover is at the claimed loca⁃tion(null hypothesis),and H1represents the case where a mali⁃cious prover is not at the claimed location.In Fig.2,the output Y of an LVSis also binary,and its realizations are D0and D1.For a given X,the probabilities P(Dj│Hi)(i=0,1,j=0,1)represent the probabilities of deciding on an output Y.The P(Dj│Hi)determines the performance of an LVS[41].The tradi⁃tional method for evaluating a detection system involves using the Neyman-Pearson Lemma,which itself is based on the false positive and detection rates.The false positive rate is the prob⁃ability of deciding incorrectly that a legitimate prover is mali⁃cious and is given byα=P(D0│H0).The detection rate is the probability of deciding correctly that a prover is malicious and is given byβ=P(D1│H1).Both these rates are functions of T andλ.We expect an LVSto provide a high detection rate and low false positive rate,but there is a tradeoff between the false positive and detection rates.The receiver operative curve(ROC)is used to demonstrate this tradeoff and is constructed by plottingβversusα.However,the ROC itself does not pro⁃vide an optimized setting[41].The Neyman-Pearson Lemma states that the likelihood ratio test maximizes the detection rate for any given false positive rate[63],[64].The likelihood ratio is the ratio between the probability density functions of the measurements under H0and H1,and the corresponding thresh⁃old T is derived by assuming a falsepositive rate.However,us⁃ing such a method to determine T does not completely optimize an LVS[63],[64].

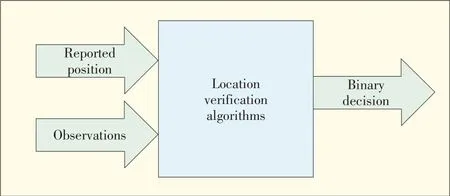
▲Figure1.A generic location verification system.

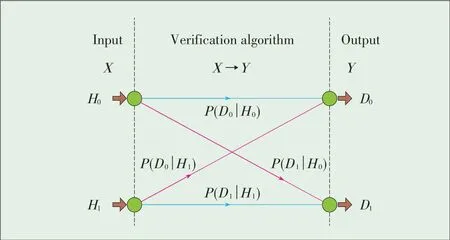
▲Figure2.Statistical decision theory model for an LVS[4].

2.3 Optimization Frameworksfor an LVS

To optimize an LVS,some unique evaluation criterion should be used as the performance metric.The transition prob⁃abilities between X and Y determine the performance of an LVS;thus,a unique evaluation criterion should be a function of such transition probabilities.

Onewidely used metric is Bayesaveragecost,given by[64]

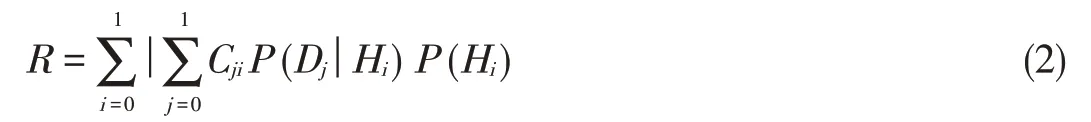
where Cjiis the cost assigned to the decision Dj(given the hy⁃pothesis Hi),and P(H0)and P(H1)are the a prioriprobabilities of the occurrence of H0and H1,respectively.In this Bayesian framework,the optimal location verification algorithm is the one that minimizes R.The Bayes average cost requires a priori knowledge of both Cjiand P(Hi).If Cjiis unknown,the MAP criterion can be used[64].According to this criterion,the uniquecost isgiven by

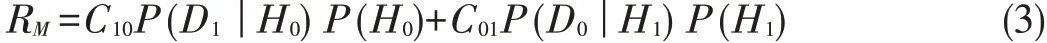
Comparing(2)and(3),we can see that RMis a special case of R,where C00=C11=0,and C10=C01=1.Thus,the MAP criterion is well suited for scenarios where the cost of rejecting a legitimate user is equal to that of accepting a malicious user.In addition,RMcan be reduced to the“total error”when P(H0)=P(H1)=0.5[52].

Although Bayes average cost,MAP,and total error can be used to optimize an LVS,they all possess a weakness in that they all depend on subjective cost values.With Bayes average cost,we have to predetermine the costs for all possible deci⁃sions.However,properly determining the true cost to the net⁃work for each decision is practically impossible.For example,what is the detailed cost to a VANET when one vehicle spoofs its location information?The true cost is subjective and de⁃pends on numerous factors and scenarios.Similarly,C10and C01are both set to one in the MAPcriterion and total error,but the cost of accepting a malicious prover is likely much higher than that of rejecting a legitimate prover.

To solve this subjective problem when optimizing an LVS,an information-theoretic framework has been proposed[40],[41].In thisframework,the cost of each possible decision isas⁃signed objectively,not subjectively.The mutual information between the system input and output is used as the optimiza⁃tion criterion.The mutual information between X and Y is de⁃fined as where H(X)is the input entropy,which measures the uncer⁃tainty of the system input(determined by the a priori probabili⁃ties);and H(X│Y)is the conditional entropy of X for a given Y.The conditional entropy measures the uncertainty of the in⁃put given the output,which is determined by the a priori and transition probabilities.Thus,I(X;Y)measuresthe uncertain⁃ty reduction of the input given theoutput,and I(X;Y)ismaxi⁃mized by the optimal information-theoretic location verifica⁃tion algorithm.Compared with the Bayesian framework,the in⁃formation-theoretic framework only assumes knowledge of the aprioriprobabilities.

Although the likelihood ratio is the optimal test statistic in most frameworks,it is difficult to obtain in practice without making some assumptions about an attacker's behavior and lo⁃cation.The likelihood function under H1is depends on the ma⁃liciousprover's attack strategy and true location,both of which are a priori unknown to the LVS.The effect of these key uncer⁃tainties with regard to optimizing the LVSis discussed in the following.

3 Location Verification in VANETs

3.1 Location Verification Based on Binary Decision Rules

The authors in [21]exploited specific properties of VANETs,such as high node density and mobility,and pro⁃posed an autonomous scheme and cooperative scheme for de⁃tecting and mitigating false locations.The acceptance range,mobility grade,and vehicle density were used in the binary de⁃cision rule of the autonomous scheme,and the thresholds were based on maximum communication range,maximum velocity,and maximum density,respectively.The test statistics used in the cooperative scheme included neighbor tables and could on⁃ly be obtained through cooperation between neighboring vehi⁃cles.The decision about a prover's claimed location is made by combining the local decisions with weight factors.The pro⁃posed location verification scheme is applied in loca⁃tion-based routing protocols,and it is assumed that a mali⁃cious vehicle does not forward the packet to the correct next hop.Therefore,the packet delivery ratio can be a performance criterion.

The proposed schemes in[21]provide the basis of location verification in VANETs.Similarly,the authors of[29]pro⁃posed location verification algorithms based on communication range,velocity and density but extended their test statistics to include travelled distance and map location.

The authors of[22]used the timestamp of a packet that had been sent(the claimed location is embedded within this time⁃stamp)in order to detect malicious vehicles that spoof location information in a VANET.The timestamp check ensures that the received packet is neither too old nor too early.In[22],a rate-limiting mechanism was proposed.If the rate of packets originating from a prover exceeds a predetermined maximum packet transmission rate,the prover is considered malicious.In thecontext of location-based routing,thepacket delivery ra⁃tio can be a performance criterion.However,packet end-to-end delay[21]is also a viable metric in scenarios where a malicious vehicle is assumed to not be forwarding the packet tothecorrect next hop.

In[24],a secure,no-infrastructure,cooperative LVS was proposed.This LVSwas designed to prevent an attacker from falsely claiming it is further away from a verifier than it actual⁃ly is.In this scheme,the verifier first estimates the prover's lo⁃cation according to time difference of arrival(TDOA)measure⁃ments.To do this,the verifier enlists the help of a neighbor that is common to both the verifier and prover.Then,the Eu⁃clidean distance error between the estimated and claimed loca⁃tions of the prover is compared with a distance related to the expected processing delay(assuming a legitimate prover).The packet delivery ratio and end-to-end delay are used to evalu⁃ate the proposed location verification algorithm because the routingprotocolsarelocation-based[24].

In[23]theauthorsused onboard radar systemstoverify ave⁃hicle's claimed location(obtained through a GPS).Taking noise into account,the authors separately determined the GPS position tolerance shadow and radar position tolerance shadow.The proposed algorithm accepts the prover's claimed location if there is an intersection between the GPSand radar position shadows(or viceversa).

The threshold and performance of the proposed location veri⁃fication algorithm are determined by the accuracy of the GPS and radar systems.The time required to detect a malicious us⁃er is the evaluation criterion.Again,in[23],routing protocols are location-based,and packet end-to end delay and delivery ratio are also used.In[27],the authors of[23]also proposed a passive location verification algorithm that can work when the onboard radar is not available or cannot work because of obsta⁃cles.This passive algorithm creates a track record of location reports by using neighbor tables.A vehicle's neighbor table contains a list of other vehicles'identifications and locations that are within its range.If a prover's claimed location greatly deviates from the track record,the algorithm deems the prover malicious.

In[28],a location-verification algorithm for VANETs with location-based routing was proposed.This algorithm is based on a trusted neighbor(i.e.a vehicle whose location has been verified)and is executed in two steps.First,the time of arrival(TOA)of the challenge-response message between the verifier and prover is used to detect distance reduction attacks.Sec⁃ond,the verifier cooperates with one of its trusted neighbors to verify that the prover is at an intersecting region determined by the verifier and trusted neighbor.The area of the intersecting region istheperformancecriterion.

In[31],the authors described a scheme in which a verifier measures the time taken for a challenge-response message to travel from the verifier to the prover and back again.Then,the estimated timeframe is calculated according to the prover's claimed location,and the two timeframes are compared.The authors of[31]conclude that this easily deployable scheme would be reliable in rural,urban,and Manhattan scenarios.

To overcome the non-line-of-sight(NLOS)problem in loca⁃tion verification systems,a cooperative LVS was proposed in[37].The proposed scheme was designed so that a verifier could verify an NLOSprover.To estimate the distance between the prover and verifier,the protocol requests help from a coop⁃erative vehicle that has LOScommunication with both the prov⁃er and verifier.The distances between the cooperative vehicle and the prover,and from the cooperative vehicle to the verifier can be estimated using,for example,TDOA or TOA.Thisthen allows for the distance between the prover and verifier to be calculated.

In addition,the distance between the verifier and prover's claimed location can be calculated.The main point of this pro⁃tocol is its ability to verify the locations of vehicles that could not otherwisebeverified becauseof obstacles.

The authors of[42]proposed a location verification algo⁃rithm dedicated to VANETs.A moving verifier(vehicle)can verify a static prover's claimed location without the assistance of roadside units or neighboring vehicles.With this algorithm,the moving verifier measures the TOA of signals transmitted by the static prover at three different locations along the moving verifier'strajectory.

Then,multilateration is used to determine the location of the prover from the three measurements.The Euclidean distance error between the prover's estimated and claimed locations is used as the test statistic,and the corresponding threshold is the average position estimation error.The test statistics and performance criteria used in the location verification algo⁃rithmsdescribed in this subsection are shown in Table 1.

3.2 Location Verification Using ROCs

A location-verification scheme based solely on messagesex⁃changed between neighboring vehicles was proposed in[25].Theauthorsfocused on detectinga maliciousvehicle that false⁃ly claims its position is as far away as possible(but within range)from the packet sender.This means that,when geo⁃graphic routing protocols are used,the vehicle will be selected as the next hop.In[25],it isassumed that each vehicle has two directional antennas—forward and backward—and that each vehicle constructs two corresponding tables of one-hop neigh⁃bors.A decision about a prover is made by exchanging and comparing neighbor tables.The theoretic detection rate is de⁃rived as a function of the vehicle density.The higher the net⁃work density,the higher the probability that malicious vehicles will bedetected in theproposed system.

A location-verification algorithm based on a vehicle's one-hop connectivity with other vehicles was proposed in[32].With this algorithm,one-hop information is exchanged be⁃tween vehicles so that each vehicle can create a two-hop neighborhood connectivity diagram.Each vehicle then uses these diagrams to verify the location information being passed to it.Each vehicle constructs a plausibility area.If vehicle A cannot directly hear vehicle B because vehicle B is two hops away,then vehicle A should not be able to directly hear from a prover that claims to be further away than vehicle B.In[34],a map-guided trajectory-based location verification algorithm was proposed.With this algorithm,a plausibility area is con⁃structed by using a prover's historical location and map infor⁃mation(e.g.road dimensions).To prevent a distance-enlarge⁃ment attack in a VANET,the authors of[38]also proposed a cooperative verification algorithm to verify a prover's claimed location.In this scheme,both the verifier and cooperating par⁃ty can measure the TOA of the challenge-response messages fromaprover.

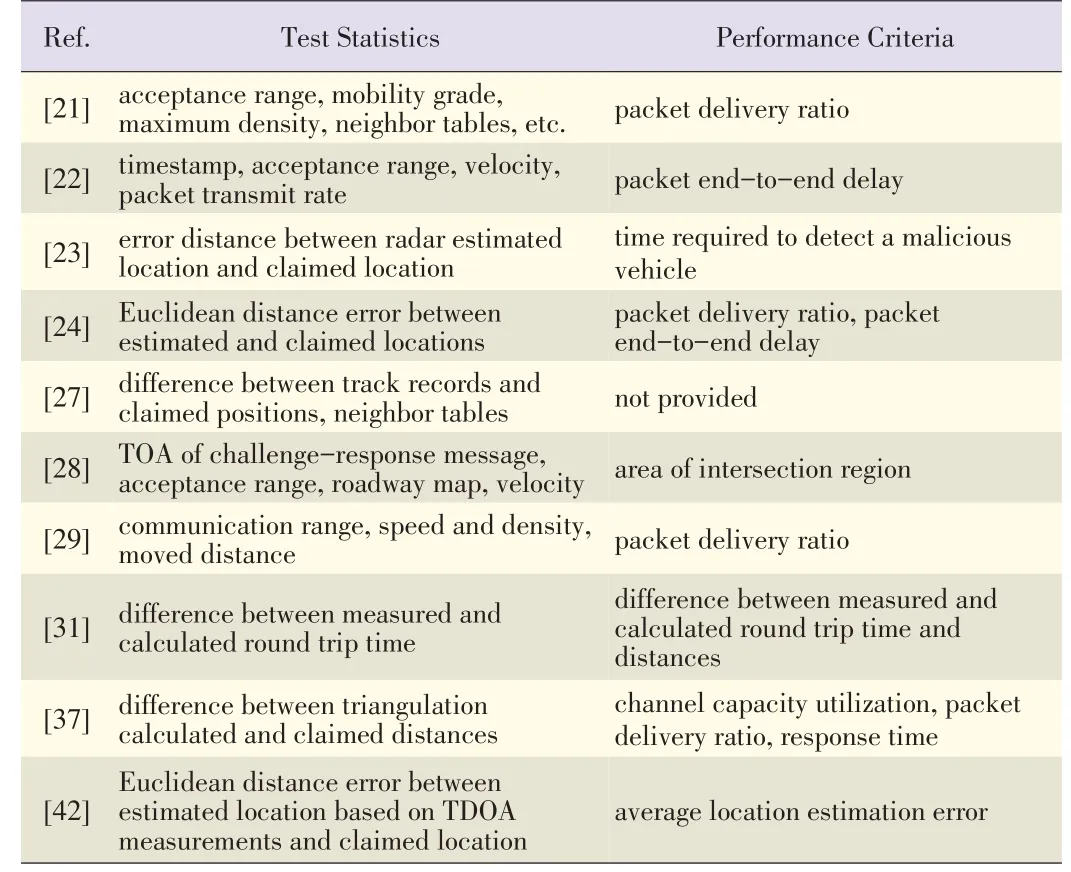
▼Table1.Binary-decision,rule-based location verification algorithms for VANET

By using such TOA measurements,both the verifier and co⁃operating party can locally verify whether the prover launched a distance-reduction attack.Within this location verification algorithm,the test statistic is the difference between the TOA-calculated distance and the distance derived from the prover's claimed location.The threshold is determined by us⁃ing the processing delay of the challenge-response message.The cooperating party is selected so that the prover is located between the verifier and cooperating party.Therefore,the pro⁃posed cooperative algorithm can detect the distance-enlarge⁃ment attack.In the simulations run in[38],the detection rate isused toevaluatetheproposed LVS.

In contrast to the previously reviewed works,which focus on the one-hop location verification,[43]proposes a bea⁃con-based trust management system.This system combines one-hop and multihop verification algorithms to thwart inter⁃nal attackersin VANETs.Theauthorsused the cosine similari⁃ty[23]between theestimated vector(includingposition and ve⁃locity)and claimed vector in order to determine the beacon trustworthiness of a neighboring vehicle.The Tanimoto coeffi⁃cient between historical beacon messages and received event messages is used to calculate the one-hop event trustworthi⁃ness.An algorithm based on this one-hop even trustworthiness is then used to determine the multihop trustworthiness of an event message.Then,the Dempster-Shafer theory[65]is ap⁃plied to combine all local event trustworthiness and determine the overall trustworthiness of an event message.Finally,an overall decision about the beacon message is made by compar⁃ing the overall trustworthiness with a trust threshold.Both the falsepositiverateand detection rateareperformancecriteria.

Sybil attacks may also compromise some location-based ser⁃vices in VANETs.A Sybil attack refers to a scenario in which a malicious vehicle illegitimately adopts multiple identities or locations to launch its attack.This type of attack may be launched by a selfish driver to mimic traffic congestion at some location on the road.It may be used to deter other vehi⁃cles from transiting along the driver's path.To detect such at⁃tacks,two location verification algorithms based on RSSmea⁃surements were proposed[44].In the first algorithm in[44],the verifier estimates the prover's location through the mini⁃mum mean-square error on the distribution of RSSmeasure⁃ments.Then,the distance error between the estimated and claimed locations is used as the test statistic.In the second al⁃gorithm in[44],the test statistic is derived from the distribu⁃tions of distance errors under H0and H1,and the threshold is derived from a given false positive rate.In the simulations run in[44],thedetection rateistheperformancecriterion.

The test statistics and performance criteria used in the loca⁃tion verification algorithms reviewed in this subsection are shown in Table 2.

3.3 Information-Theoretic Location Verification Systems

In[40],the verifier uses the maximum likelihood estimator to estimate a prover's location based on RSSmeasurements.The Mahalanobis distance error between the estimated and claimed locations of the prover is used as the test statistic in the binary decision rule.The corresponding threshold is select⁃ed by maximizing the mutual information between the input and output of the LVS.A threshold selected in this manner does not completely optimize an LVSbecause the test statistic isnot optimized.

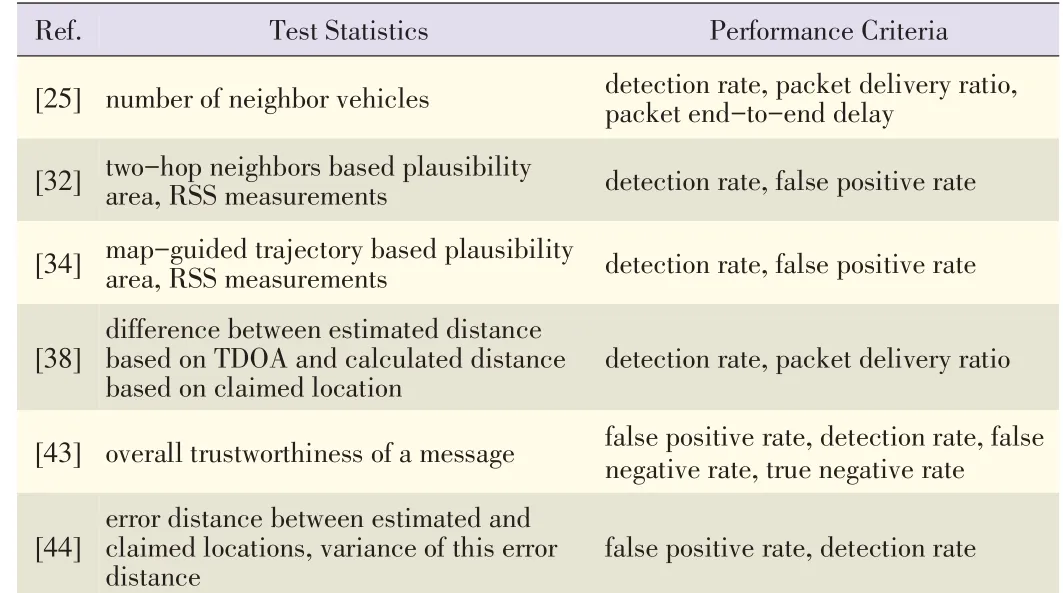
▼Table2.Location verification algorithmsusing ROCsfor VANET

The authors of[41]proved that the likelihood ratio is the op⁃timal test statistic in terms of maximizing the mutual informa⁃tion between theinput and output of an LVS.

With such a test statistic,an optimal information-theoretic LVSwas obtained.To deploy the optimal information-theoret⁃ic location verification,three threat models were proposed[41].In these models,the likelihood functions for RSS mea⁃surements could be obtained or approximated in closed forms.The information-theoretic and MAP frameworks lead to the same decision rule(likelihood ratio test with the same thresh⁃old)in the special case where P(H0)=P(H1)=0.5 and the like⁃lihood functionsunder H0and H1follow Gaussian distributions with thesamevariance.

The authors of[41]showed the objective nature of the opti⁃mization metric discussed in subsection 2.3.They also showed another useful property of an information-theoretic framework:The optimized threshold is not very sensitive to the a priori probabilities(Fig.3).Theoptimal threshold in the MAPframe⁃work,which minimizes RMfor the likelihood ratio test,is a lin⁃ear function of P(H1)(Fig.3).This can be explained by the fact that the optimal threshold for minimizing RMis P(H0)/P(H1)[64].

However,the optimal threshold in the information-theoretic framework that maximizes I(X;Y)for the likelihood ratio test converges to a constant as P(H1)approaches zero.Knowledge of the a priori probabilities is very difficult to obtain,and in practice,can only be assumed or roughly estimated.In most practical verification scenarios,P(H1)can be assumed to be quite small.Therefore,the behavior seen in Fig.3,for the opti⁃mal information-theoretic threshold,gives an information-the⁃oretic framework a significant advantage over a Bayesian framework.

4 Location Verification Applicableto VANETs

Collecting received signal strengths does not require extra hardware,so many location verification systems for general wireless networks have been developed based on RSSmeasure⁃ments.In[3],the authors proposed an algorithm to detect loca⁃tion-spoofing attacks by matching the input instantaneous measurementswith thenormal signal fingerprints.Fromexperi⁃mental results,the authors of[6]found that received signal strengths follow a mixture of two Gaussian distributions if the prover and verifier both have two antennas.To perform the ver⁃ification,a likelihood ratio test can be constructed from the in⁃stantaneous measurements and expected normal profiles[6].A location verification algorithm based on RSS fingerprints was proposed in[48].The authors observed that only analyzing the residual of RSSmeasurements is not sufficient for robustly de⁃tecting location-spoofing attacks.However,if this residual is referenced to a claimed location,the residual can provide a verification algorithmthat can resist variousformsof attack.

In[52],the location verification was formulated as a statisti⁃cal significance testing problem.The authors analyzed the spa⁃tial correlation of RSSmeasurements to detect location attacks.They derived theoretic false positive and detection rates in the one-dimensional and two-dimensional physical spaces.The authors of[52]also optimized the threshold in the proposed bi⁃nary decision rule by minimizing the total error.They proposed a location verification algorithm robust against spoofing and Sybil attacks by using clustering methods[66].The algorithms in[3],[6],[52],and[48]are similar to many RSS-based wire⁃less local verification algorithms.In principal,they can all be easily adapted tothe VANETenvironment.

Some generic challenge-response-based location verifica⁃tion algorithms for wireless networks have been proposed in[7],[45],and[50].The well-known Echo protocol is based on the delay of the two challenge-response messages sent through wireless and ultrasonic channels[45].The relative delay in the two channels is compared with the ideal theoretical delay,which is derived from a prover's claimed location.Applying the Echo protocol in a VANET requires vehicles to have both wireless and ultrasonic hardware for communication.A loca⁃tion verification protocol with hidden or mobile base stations was presented in[50].Such mobile base stations can securely estimate the distances to the prover because the locations of the hidden or mobile base stations are assumed to be unknown to the prover.The distance error,which is the difference be⁃tween the estimated and claimed locations of a prover,is com⁃pared with a threshold as a means of verification.This algo⁃rithm can be used in a VANET if the locations of some verifi⁃ers are not publicly known.In[7],several location-verification algorithms were proposed.These algorithms use a power-mod⁃ulated challenge-response method to detect malicious vehi⁃cles.Adopting a power-modulated location verification algo⁃rithm to a VANET would be straightforward if the verifier in a VANETcould adjust its transmit power.

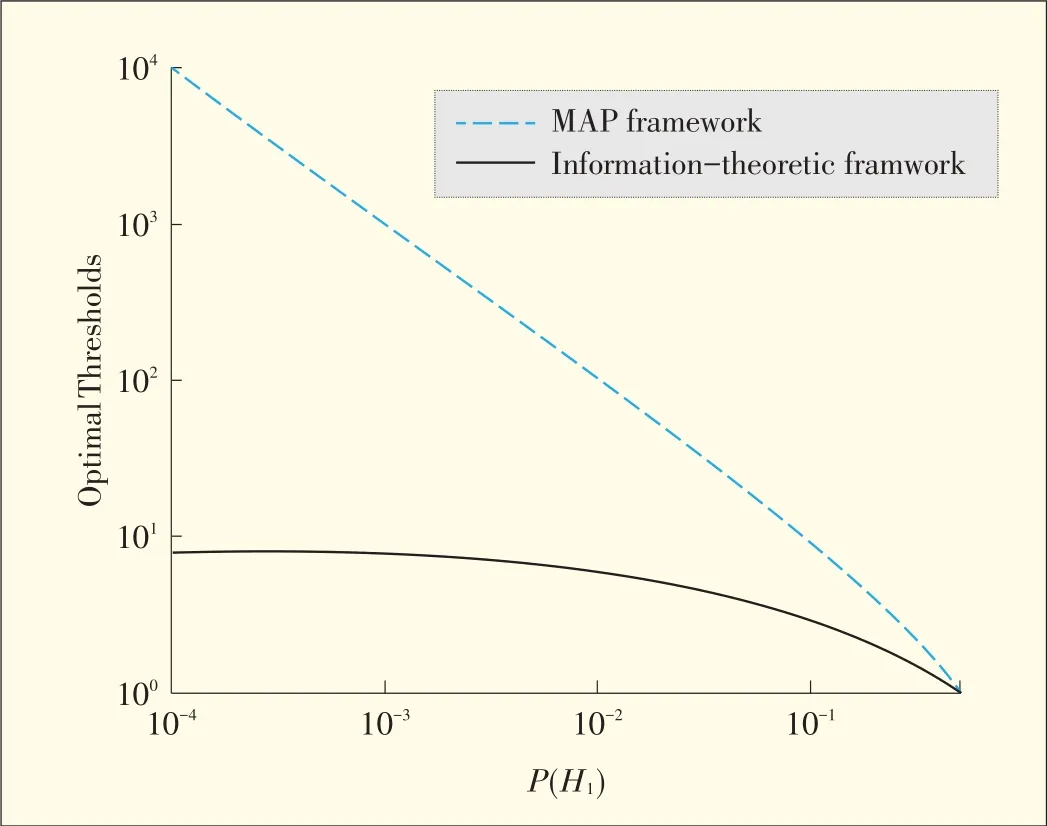
▲Figure3.Optimal thresholdsfor information-theoretic and MAP frameworksasfunctionsof P(H)[41].

The authorsof[51]proposed a probabilistic location verifica⁃tion algorithm for a wireless sensor network(WSN)with high node density.In such networks,the number of hops that a packet sent by a prover must traverse in order to reach a verifi⁃er probabilistically depends on the Euclidean distance be⁃tween the prover and verifier.The algorithm proposed in[51]verifies a prover's claimed location by checking the correla⁃tion between the number of hops and Euclidean distance(cal⁃culated from the prover's claimed location).In[54],two loca⁃tion verification algorithms were proposed for a WSN with a high node density.These algorithms exploit the inconsisten⁃cies between a prover's claimed location and the determina⁃tion of the verifier's neighbor(one hop from the verifier)that it can hear the prover.The algorithms in[51]and[54]are used in a WSN with high node density.Similarly,these algorithms require the VANETto have a high vehicle density(i.e.they are suitablefor urban scenarios).

The algorithms discussed in section 4 are a representative(but not exhaustive)selection of location verification algo⁃rithms proposed for other wireless networks.We have classi⁃fied these algorithms as RSS-based,challenge-response based,or high-node-density based.Thereareother typesof al⁃gorithmsthat could beadapted to VANETs.

5 Conclusion

In this paper,we have outlined the generic frameworks for location verification in VANETs.We have also discussed how much of the exiting literature on location verification for VANETs falls within such frameworks.With intelligent trans⁃port systems now becoming a key focus of transport depart⁃ments worldwide,deployment of actual VANETs is close to re⁃ality.A mission-critical component of such networks is loca⁃tion verification.As such,the research reviewed in this paper islikely tobeof increasingimportance.