Reducible Discord in Generic Three-Qubit Pure WStates

Zhengjun Xi,Zhihui Li and Yongming Li

(1.Collegeof Computer Science,Shaanxi Normal University,Xi′an 710062,China;

2.Collegeof Mathematics&Information Science,Shaanxi Normal University,Xi′an 710062,China)

Abstract Quantum discord is the most prominent of quantum correlations,but it does not have unique generalizations to the multipartite case.Wstates are especially useful for secure communication.In thispaper,wepropose that thequantumcorrelation in generic three-qubit pure Wstatescan begiven by thetwo-qubit discordsof thesestates.

Keyw ords quantumdiscord;Wstate;quantumcorrelation

1 Introduction

I n many-particle physics and quantum information sci⁃ence,classifying and quantifying correlations in a mul⁃tipartite quantum state is a fundamental problem.The amount of knowledge about the quantum system that can be acquired from subsystems has also yet to be deter⁃mined.Quantum science asks whether a multipartite quantum state can be determined uniquely if all itsreduced-density ma⁃trices are specified[1],[2].Generic N-party pure quantum states are uniquely determined by the reduced states of just over half the parties[3].In[4],the N-qubit pure Wstates are determined by their bipartite reduced density matrices.Thus,N-party correlations in Wstate are reducible to two-party cor⁃relations.In the simplest case,theentanglement of thegeneral⁃ized three-qubit W state has maximum robustness against the loss of one qubit.This means that the bipartite entanglement left in thesystemcan still beused toperforminformation-theo⁃retic tasks,even without the cooperation of a third party.More⁃over,a third party cannot destroy the residual entanglement,which makes the Wstate particularly useful for secure commu⁃nication[6]-[9].Almost all three-party pure quantum states can be determined by two-party reduced states[10]-[12].In[1],[10]and[11],the total quantum correlations in the N-qu⁃bit pure W states should be characterized by the bipartite quantum correlation within them.In this paper,we discuss two-qubit quantum discord in generic three-qubit pure W states[13].We propose two-qubit quantum discord as a figure of merit for quantumcorrelation in the bipartite state.

2 Quantum Discord

Here,we discuss the concepts and properties of total,quan⁃tum,and classical correlations in the bipartite quantum sys⁃tem.The total correlation in a bipartite quantum stateρABis given by the mutual information:

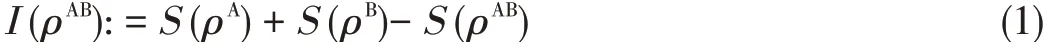
where S(ρ)is the von Neumann entropy,given by-Tr(ρlog2ρ).The reduced density matrices ofρABare denotedρAandρBand are obtained by tracing out B and A,respectively.The classical correlation is the amount of information about subsys⁃tem B that can be obtained by measuring subsystem A[14].Theclassical correlation isgiven by

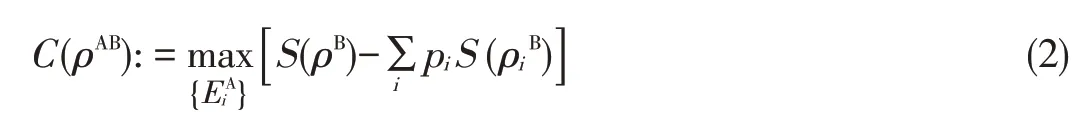
where{EiA}isthepositive-operator valued measure(POVM)performed on A,andisthe remaining state of B after obtaining outcome i on A.The probability of outcome i is given by pi=Tr(EiA⊗IBρAB),where IBis the identi⁃ty operator on the subsystem B.

Quantum discord is the difference between total and classi⁃cal correlations[13]:

Quantum states without entanglement but with nonzero quantum discord can still be used to perform useful quantum tasks[15].Quantum discord is essential in a wide variety of quantuminformation and quantumcomputations[16].

The definition of classical and quantum correlations in⁃volves an optimization process to minimize the term,which is considered the quantum version of the conditional en⁃tropy[13].For a two-qubit system,the optimal POVM is a one-dimensional projective measurement[17].In general,it is difficult to calculate the analytic expression for the quantum discord[16],[18]-[22].Analytic results have only been ob⁃tained for a few specific cases of quantum discord:Many stud⁃ies of quantum discord rely on numerical results.However,the results from[20]and[21]are sufficient for us to achieve our aimsin thispaper.

3 Quantum Discord for a Generic Three-Qubit W State

Weconsider only thecaseof athree-qubit Wstate,given by

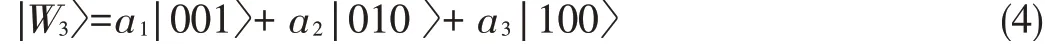
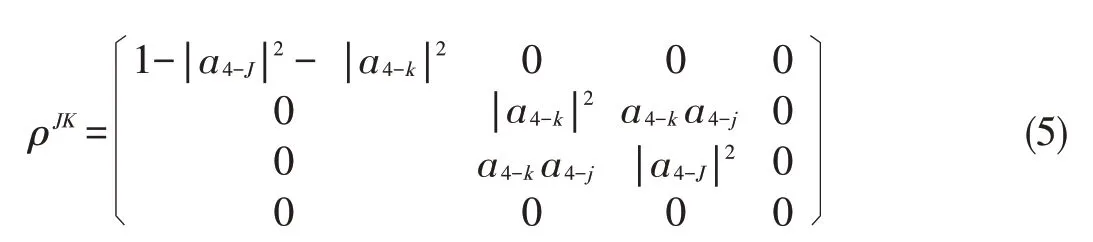
where J＜K.The one-qubit reduced density matricesρJ(k)are given by Here,we discuss quantum discord in all the two-qubit re⁃duced density matricesof thethree-qubit pure Wstate.There⁃duced density matrix(5)satisfiesthecondition

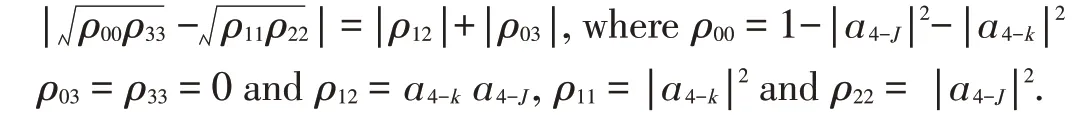
Then,from the results in[20]and[21],quantum discord DJ(ρJK)has a simple form derived from measuring J.Quantum dis⁃cord isgiven by

where S(ρK｜∏J)is the conditional entropy p S(ρK)+p S(ρK).

For each outcome i on J,theremainingstateof K isgiven by

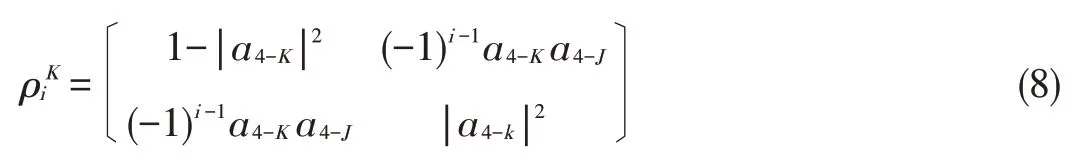
For each outcome,.Quantum discord is asymmetric when J and K systems are exchanged.Therefore,by measuring K for all the two-qubit density matrices(5),the quantum dis⁃cord can be derived:

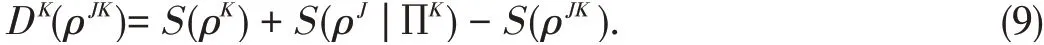
where S(ρJ｜∏K)is the conditional entropy p1S(ρ1J)+p2S(ρ2J).For each outcome i on K,theremainingstateof J isgiven by

where

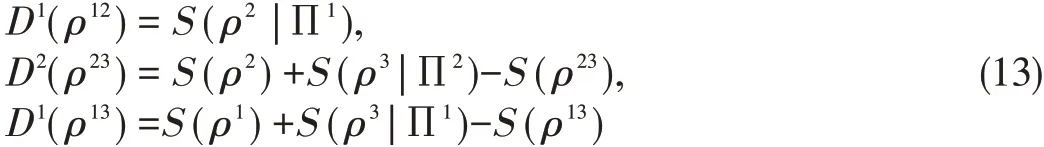
The followingcasesareshown in Fig.1:

Whenɑ=0 and｜W3〉=｜010〉,the reduced density matrices areproduct statesand D1(ρ12)=D2(ρ23)=D1(ρ13)=0.

At first,it might seem that{}con⁃flicts with the conclusions in[4]and[5].However,the reduced density matricesρ12andρ23are unitary equivalents and have the same information.In this sense,the matrices have the same position to determine the W state[4],but their discords are different.

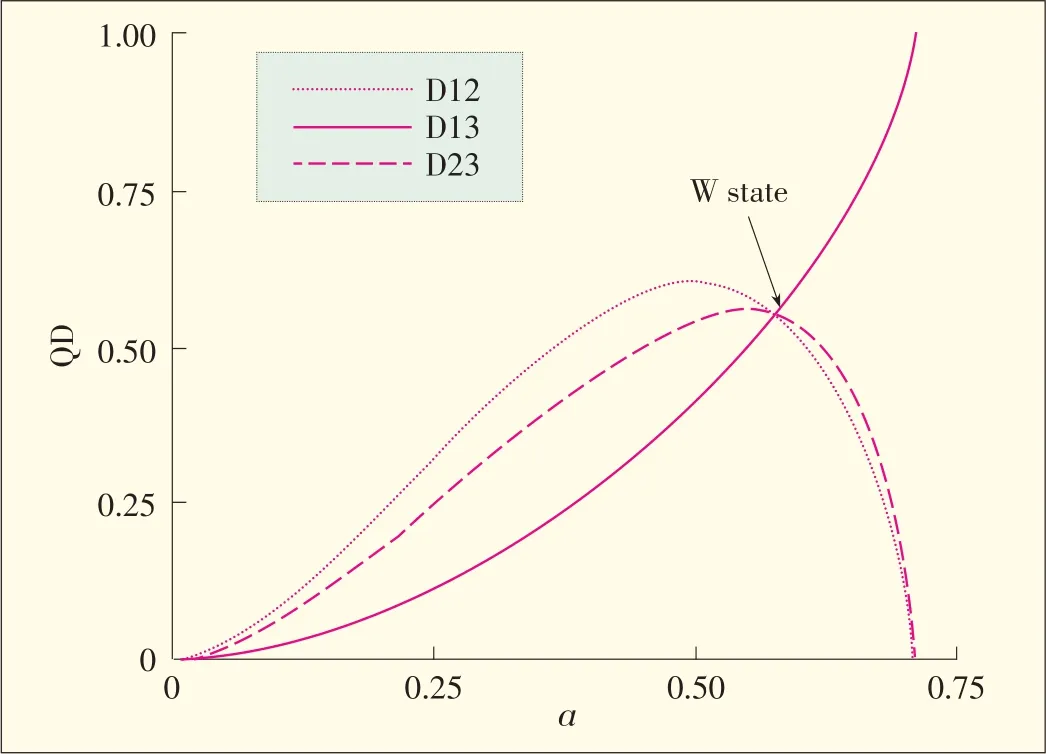
▲Figure1.Reduciblediscord in one-parametric three-qubit pure Wstates.Here,theparameterɑ1=ɑ3=ɑ∈[0,1].2

4 Conclusion

We have described how quantum correlations in generic three-qubit pure W states can be given by the two-qubit dis⁃cords of these states.Our results show that reducing discord in the generalized three-qubit pure W state is complicated.The results in this paper might also be useful in a general scenario.For example,our results could be used to verify the monogamy and entropy uncertainty relationship.