基于线性规划的气动舵重构控制分配*

臧希恒 唐 硕,2

1.西北工业大学航天学院，西安 710072 2.航天飞行动力学技术重点实验室，西安 710072

传统飞行器利用升降舵控制俯仰方向，方向舵控制偏航方向，副翼控制滚动方向，在进行飞行控制系统设计时，假设俯仰、偏航和滚转方向自动解耦，并将俯仰控制力矩指令直接转换成升降舵偏转指令，偏航力矩指令转换成方向舵偏转指令，而滚动力矩指令转换成副翼偏转指令。由于现代高性能飞行器对于任务与控制精度要求的不断提高，飞行器配备了更多的气动舵面，而且气动舵面之间存在更强的耦合。当飞行器配备的气动舵面数量超过3个，即超过俯仰、偏航、滚转3个控制方向时，称气动舵面的控制能力具有一定的冗余度。如何将俯仰、偏航和滚转控制力矩转换为气动舵面偏转指令即为控制分配问题。

由于气动舵面之间的耦合和冗余，使得将控制力矩指令转化为有效的气动舵面偏转指令具有一定难度，尤其当气动舵面存在位置和速率饱和限制时更具挑战性。如何给出合理的气动舵面偏转指令固然重要，但是当某些气动舵面存在某种硬件故障而不能正常工作时，如何尽最大的能力完成飞行器的姿态控制任务亦显得尤为重要。对于重构飞行控制系统来说，重构控制分配算法主要应用在具有多冗余执行机构的飞行器上，需要在满足位置和速率饱和约束的前提下完成控制力矩在各气动舵面之间的自动分配，并且在已知舵面出现何种故障时完成气动舵面在卡死、舵面损失、浮动等故障模式下的重构控制。重构控制分配主要应用在具有多气动舵面的航空航天飞行器，主要应用对象有战斗机、可重复使用运载器等。基于Durham在控制分配领域的研究工作，一些控制分配方法在上个世纪末得到了广泛的研究[1]。一些简单的控制分配技术如直接分配法、伪逆法和串式链分配法[1-2]，无法保证位置和速率约束得到满足。Enns提出了一种通过利用罚函数考虑位置和速率约束的最小二乘控制分配方法[3]。Paradiso首先尝试将线性规划用来解决气动舵面的控制分配问题[4]。近些年，形成了一些将控制分配问题转换为有约束优化问题来求解的方法[5-6]。现有的控制分配技术的综述性研究见文献[2]。

图1 基于控制分配的飞行控制系统

本文提出了一种将控制分配问题转化为有约束的多目标混合1范数优化问题，并将其转化为标准的线性规划模型，通过现有成熟的线性规划求解算法包即可完成控制分配问题的求解，最后利用提出的线性规划控制分配算法对亚轨道飞行器的气动舵面控制分配问题进行仿真验证，证明了算法的有效性及气动舵面故障的重构控制分配能力。

1 气动舵控制分配问题描述

控制分配在飞行控制系统中扮演重要角色，特别是在气动舵面存在饱和限制、效率差异性以及重构飞行控制中，其作用更是举足轻重。图1为采用控制分配的控制系统结构图。输入为制导系统给出的制导指令，所需控制力矩udes由基线控制律给出，用来跟踪制导指令，而udes由执行机构指令偏转δ产生，直接作用于机体。本文假设控制力矩与气动舵面偏转之间呈线性关系，即所谓线性控制分配问题，其形式如式(1)所述

udes=Bδ

(1)

给定所需的控制力矩udes和控制效率矩阵B求解执行机构指令偏转δ即为控制分配问题，同时执行机构还需满足下列位置和速率约束：

气动舵面位置约束：

δmin≤δ≤δmax

(2)

气动舵面速率约束：

(3)

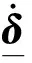
现代飞行器一般采用数字控制系统，飞行控制律为采样周期T的离散时间系统，可以将上述位置和速率约束合并为下面的组合时变位置约束。

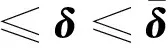
(4)

其中

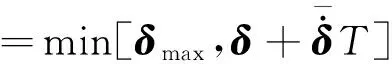
(5)

(6)

其中,L，M，N为滚动，俯仰，偏航力矩；δ=[δ1δ2…δn]T，n代表飞行器具有n个气动舵面。

故障模式下气动舵面模型：

1)卡死：由于执行机构故障，舵面卡死在某角度。舵面δi卡死在δf位置时的舵面故障模型通过修改相应的位置与速率约束来实现，如式(7)和(8)所示：

δf≤δi≤δf

(7)

(8)

2)舵面积损失：由于热烧蚀或其它原因造成了部分舵面的缺失，舵面仍具备产生操纵力矩的能力，但能力降低。假设舵面积与所产生的操纵力矩成正比。若舵面δi缺失面积占舵面积的比率为p，则舵面δi的故障下模型可通过将效率矩阵B的第i列乘以(1-p)来表示：

(9)

3)浮动：舵面随气流浮动，丧失了产生气动力矩的能力，即对各轴的力矩贡献为零。舵面δi在浮动故障模式下的模型可通过将效率矩阵B的第i列置为0来表示：

(10)

2 控制分配的线性规划描述

首先将上一节中的控制分配问题转换为具有下面性能指标的有约束优化问题：

(11)

约束于

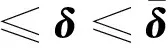
(12)

最小化性能指标范数的选择决定了优化问题的求解算法，这里选择1范数，可以利用线性规划求解器求解控制分配问题，这也是目前控制分配最便捷也是最高效的求解方法。

2.1 控制能力不足优化层

当气动舵面不足以实现给定俯仰、偏航和滚动三轴的控制力矩时，称气动舵面的控制能力不足。此时控制分配问题即为方程(13)所示的力矩误差最小化问题，

(13)

约束于方程(10)。其中Wu为对角权重矩阵，给定了对俯仰、偏航、滚动三轴力矩误差的惩罚。

下面将式(13)和(12)所示的气动舵面控制分配问题转化为标准的线性规划模型。首先定义一个松弛向量，

usudes-Bδ

(14)

us代表了滚转、俯仰和偏航三通道的力矩误差。通过选取us作为决策变量，方程(13)所描述的1范数优化问题可以转化为(15)所示的标准线性规划模型，

(15)

约束于

(16)

式(15)和(16)所示的线性规划模型物理意义简单明了，在满足气动舵面位置和速率约束的前提下，实现三轴力矩误差的最小化。

2.2 控制能力充足优化层

当式(15)的性能指标J=0时，称气动舵面的控制能力充足。此时控制分配问题需要在完成式(15)所示的力矩误差最小化后，继而进行控制能力充足优化层，完成关于气动舵面的第二性能指标的优化，即式(17)所示的控制最小化问题，

(17)

约束于式(10)。其中δp为偏好舵偏，Wδ为的对角权重矩阵，给定了对气动舵面的惩罚。

同样地，式(17)和(12)所示控制最小化问题可以转化为式(18)和(19)所示标准线性规划模型。

(18)

(19)

其中，δs为松弛向量，δs代表了实际舵偏与偏好舵偏的差值。

2.3 多目标混合1范数优化

通过引入正数ε可以有效地将上面两节中的误差最小化与控制最小化两层优化问题转化为方程(20)所示的具有2个优化目标的混合1范数多目标优化问题，这样处理将上面的两层优化问题转化为一层优化问题，而且简化了问题的求解并减轻了计算负担。

(20)

同理，可以将其转为式(21)和(22)所示的标准线性规划问题，该线性规划问题具有n+3个决策变量，式(22)为线性规划的各种线性不等式约束。

(21)

(22)

3 数值实例

本文选取某亚轨道飞行器为仿真验证对象，该飞行器具有副翼、方向舵、升降舵和体襟翼4个气动舵面。副翼主要用来控制滚转，方向舵控制偏航，而升降舵和体襟翼则用来控制俯仰方向。滚转和偏航方向具有较强的交联耦合作用，而在有侧滑时俯仰与滚动方向也会产生较强的交联耦合作用，同时飞行器气动舵控制能力在俯仰方向具有一定的冗余度。现选取亚轨道飞行器再入返回时的一个低速状态来验证在气动舵面无故障模式下和体襟翼卡死5°时，对于具有交联耦合和冗余的复杂气动舵面系统控制分配算法的有效性和重构控制能力。体襟翼卡死故障模式将会对俯仰方向产生一个近似常值干扰力矩，同时在有侧滑状态下将会对滚动和偏航方向产生交联耦合作用。低速飞行状态见表1。

如图1所示，图中基线控制律模块将采用基于反馈线性化的滑模控制方法为控制分配模块提供期望控制力矩，基于反馈线性化的控制器设计方法详见文献[7]。气动舵面的位置与速率约束见表2。

表1 初始飞行状态

表2 气动舵面位置速率约束

给定攻角15°、侧滑角0°与倾斜角0°三通道的阶跃制导指令，仿真步长设为T= 0.01s，控制分配参数分别选为：

ε=0.01。

运行仿真8s，气动舵面无故障模式和体襟翼卡死5°的姿态角响应曲线对比如图2，气动舵面无故障模式下攻角和倾斜角的跟踪比体襟翼卡死5°时攻角和倾斜角的跟踪快速、性能好。由于体襟翼和升降舵同时用来控制俯仰方向，故俯仰气动舵面控制能力具有一定的冗余，因此体襟翼卡死5°时，尽管攻角的响应快速性有所降低，但是攻角仍然可以实现稳定跟踪，验证了控制分配算法具有故障重构控制能力。由于体襟翼卡死在5°所带来的滚动干扰力矩，造成了倾斜角跟踪性能的下降。图3和图4分别为无故障模式和体襟翼卡死5°时对应的气动舵偏转指令。仿真结果表明本文所提出的气动舵面控制分配算法在不需要控制律重构的前提下，有效地解决了气动舵面的控制分配问题，并实现了气动舵面故障下的重构控制。

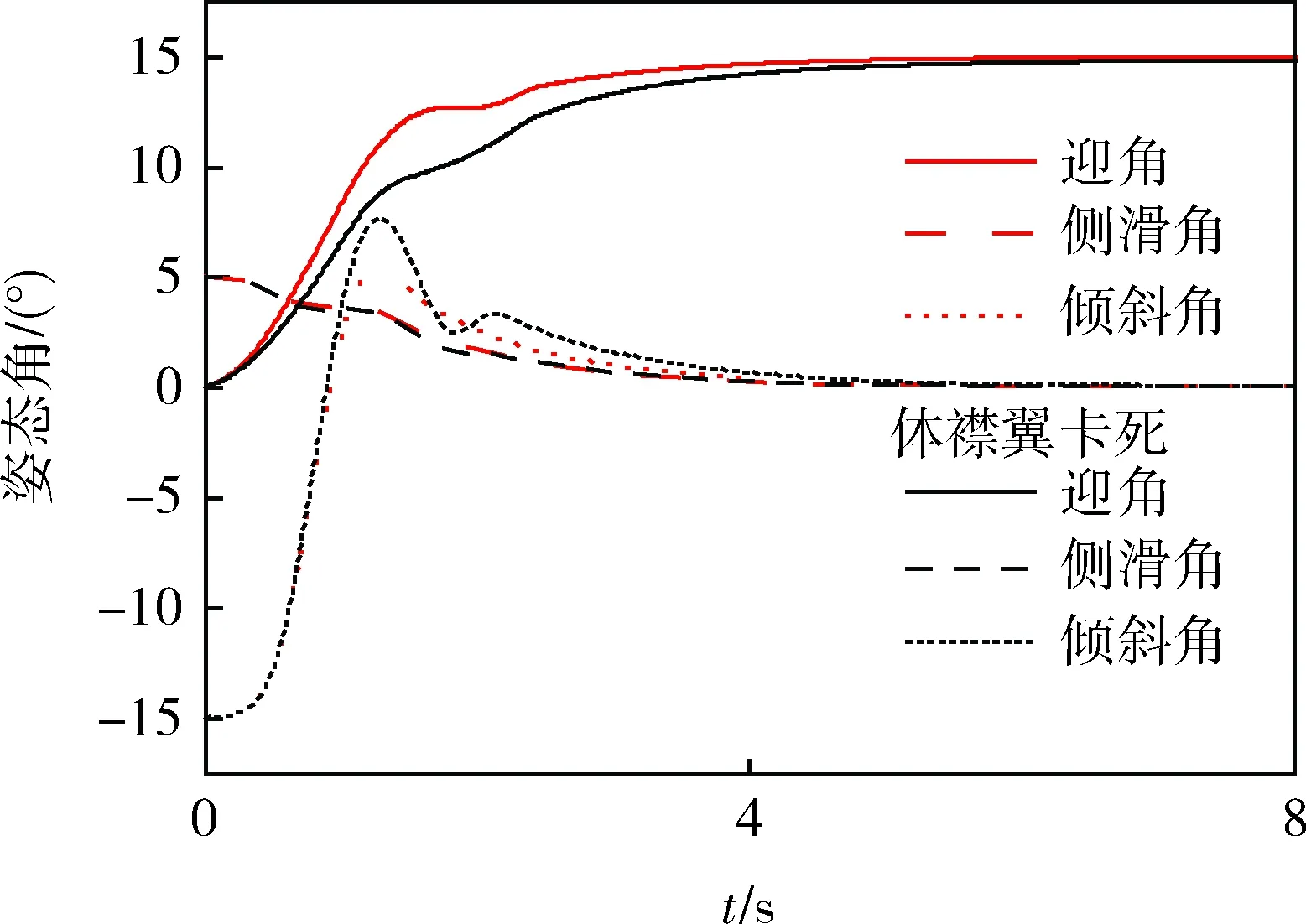
图2 姿态角响应曲线

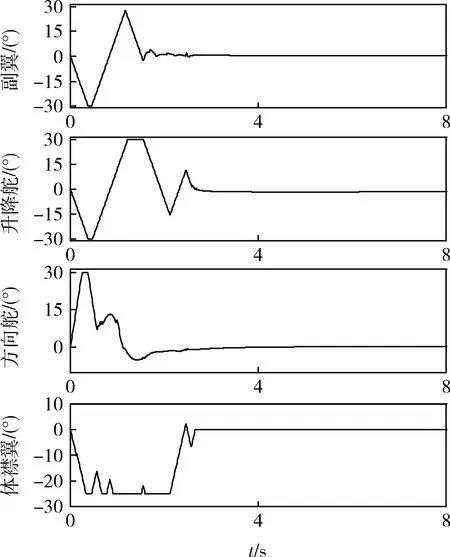
图3 气动舵偏转指令：无故障模式

图4 气动舵偏转指令：体襟翼5°卡死

4 结论

1)针对飞行器气动舵面控制分配的特点，将控制分配问题转化为有约束的2层优化目标1范数优化问题和多目标的混合1范数优化问题。

2)将相应的有约束1范数优化问题转化为标准的线性规划模型，简化了控制分配问题的求解。

3)对于亚轨道飞行器气动舵面的控制分配问题，仿真结果表明，所提出的控制分配算法是有效的，并具有气动舵面故障模式下的重构控制能力。

参 考 文 献

[1] Durham W C.Constrained Control Allocation[J].Journal of Guidance, Control, and Dynamics, 1993, 16(4): 717-725.

[2] Bodson M.Evaluation of Optimization Methods for Control Allocation[J].Journal of Guidance, Control, and Dynamics, 2002, 25(4): 703-711.

[3] Enns D.Control Allocation Approaches[J].AIAA-98-4109, 1998.

[4] Paradise J A.Adaptable Method of Managing Jets and Aerosurfaces for Aerospace Vehicle Control[J].Journal of Guidance, Control, and Dynamics, 1991,14(1): 44-50.

[5] John A M Petersen, Bodson M.Interior-Point Algorithms for Control Allocation[J].Journal of Guidance, Control, and Dynamics, 2005,28(3): 471-480.

[6] Tor A.Johansen, Thor I.Fossen, Petter Tøndel.Efficient Optimal Constrained Control Allocation via Multiparametric Programming[J].Journal of Guidance, Control, and Dynamics, 2005,28(3): 506-515.

[7] 韩艳铧, 周凤岐,周军.基于反馈线性化和变结构控制的飞行器姿态控制系统设计[J].宇航学报, 2004,6(25): 637-641.(Han Y H, Zhou F Q, Zhou J.Design for Aerocraft Attitude Control System Based on Feedback-linearization and Variable-structure-control[J].Journal of Astronautics, 2004,6(25): 637-641.)