基于虚拟目标的大气层内拦截弹中制导律研究
李 爽 江 涌 张奕群 李君龙
1.北京电子工程总体研究所,北京 100854 2.航天科工集团防御技术研究院,北京 100854
对于侧窗探测问题,国外从上世纪90年代开始,为发展战区导弹防御系统,对其开展了大量的研究,目前已掌握了该技术。但现有应用大都在大气层高层拦截器上,中末制导交班对视场角的要求可以通过调整姿态来满足。而在大气层内拦截弹上,姿态的微小调整就会引起较大的力矩,视场角的要求不能通过姿态调整来满足。我国近年来开始关注侧窗探测问题,重点关注侧窗口的设计、冷却等问题,以及侧窗探测下的姿态控制和跟踪问题[1-2]。
比例和优化导引律历来都是理论和实践工作者关注的焦点[3]。其中文献[4]通过在比例导引的基础上添加一个时变偏置项,满足了脱靶量为0和末端攻击角约束。由于比例导引的种种优点,不少人突破末段寻的制导的思路,通过设置虚拟目标,将其应用于中制导技术,其中最常见的虚拟目标是由目标运动特性得到的预测命中点。本文针对导引头侧窗探测和大气层的特点对中制导提出的预测脱靶量为0和特定视场角要求,提出一种新的虚拟目标的设置方法,并根据所设置虚拟目标对中制导律进行优化,从而获得满足交班要求的中制导弹道。文中的末制导预测脱靶量是指拦截弹在中制导末端时刻相对于实际目标的瞬时脱靶量。
1 约束条件的分析和虚拟目标的设置
为了简化弹道特征的研究,作如下假设:
1)拦截弹与目标的交战只在纵平面内进行;
2)实际目标的弹道为直线弹道,且速度大小VT和拦截弹速度大小V均为常量;
3)中制导末端过载指令为0,攻角接近于0。
根据以上假设,以及虚拟目标的设置思想绘出虚拟目标与实际目标、拦截弹的位置关系示意图如图1所示。
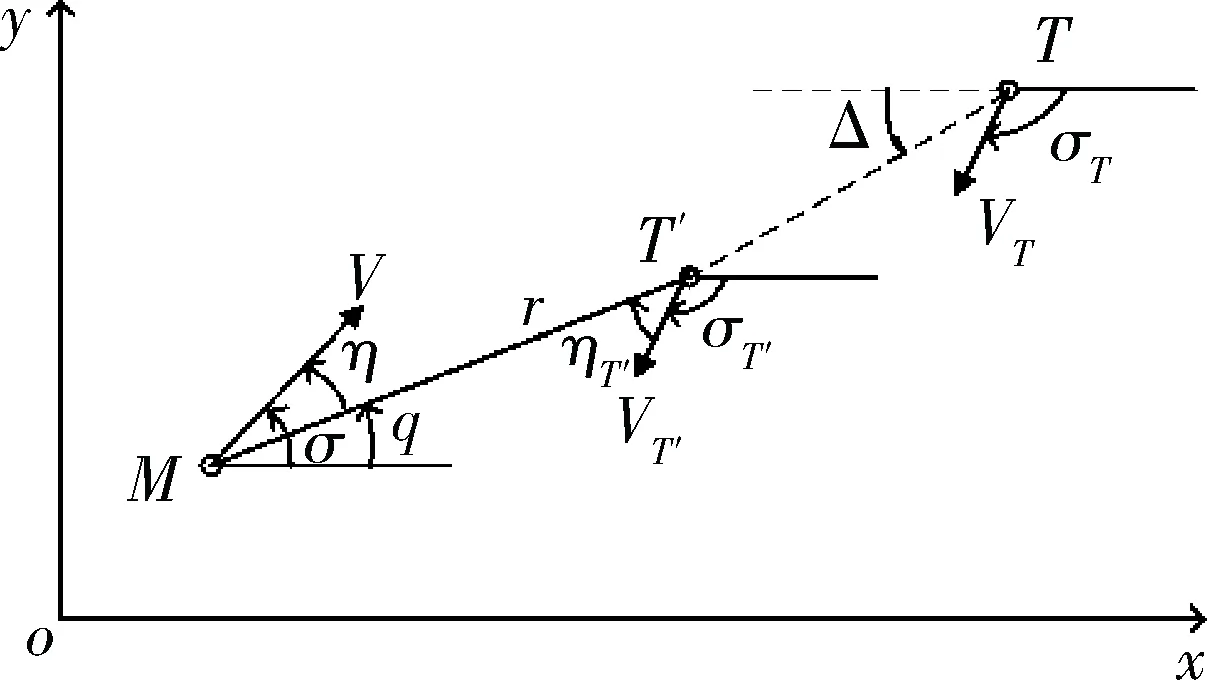
图1 虚实目标与拦截弹位置关系
基于图1,本文的研究内容可以形象的描述为:根据测得的M和T的当前位置和速度,研究T′(xT′,yT′)的位置和运动状态的设置方法,以及相应的导引律的优化设计,使拦截弹在该导引律的作用下,针对T′的中制导段结束时,实际目标T正好落在拦截弹的视场范围内,且针对实际目标的预测脱靶量为0。
简单起见,此处假设虚拟目标和实际目标具有相同的飞行速度,即两者在运动过程中相对静止。对拦截过程和交班条件进行详细分析,可以得出虚拟目标需要满足以下要求。
1.1 初始位置约束
中制导初始时刻,在拦截弹和目标的初始位置M0(xM0,yM0)和T0(xT0,yT0)测得的情况下,虚拟目标的初始位置T0′(xT0 ′,yT0 ′)可以定义如下
(1)
假设末制导段导引头的视场距离L=|TT′|给定,则结合方程组(1)得拦截弹和目标的初始位置对Δ,q0构成下面的约束
(2)
1.2 标准视场角约束
(3)
为了不失一般性,也可将上述ξ*定义为末制导开始时刻的视场定向基准位置。
若拦截弹与T′交会时的攻角为αk,如图2所示。
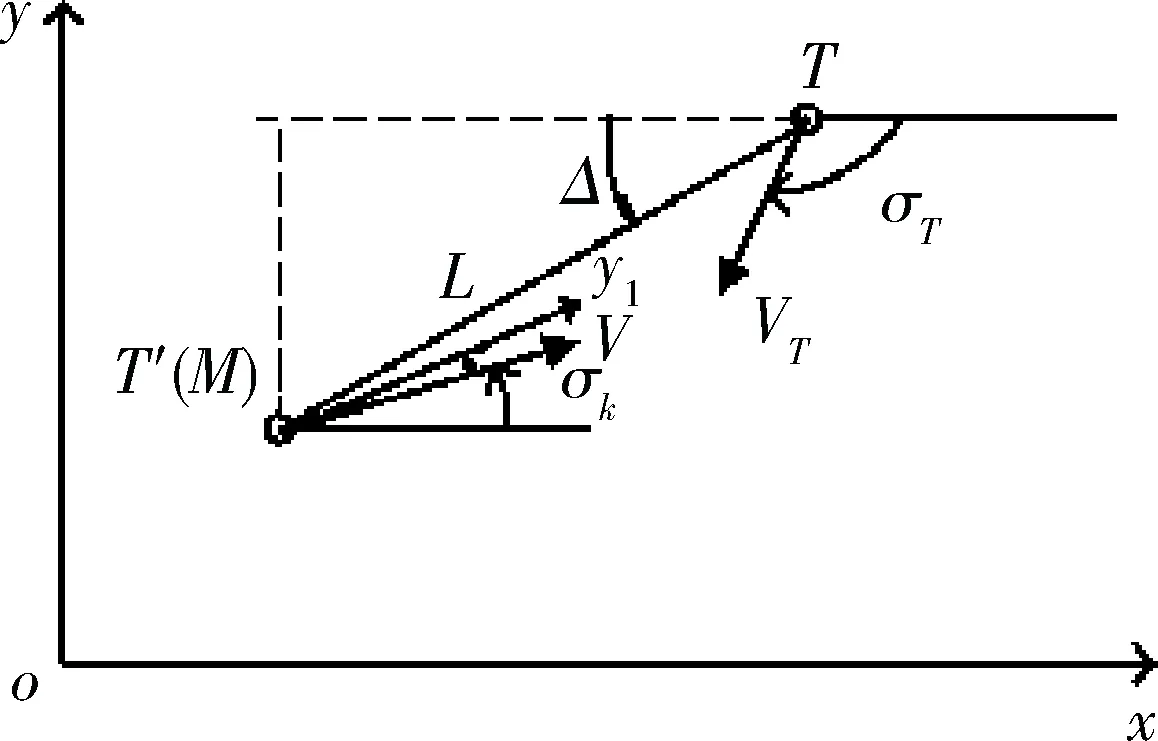
图2 末段交会示意图
则此时目标所处视场角位置
ξk=Δ-(σk+αk)
(4)
在过载为0的情况下,联立式(3)和(4),得设计过程中的标准视场角约束
Δ-σk=ξ*
(5)
1.3 零预测脱靶量条件
根据预测脱靶量的定义,以及图2所示的末段交会示意图,可以得出末制导预测脱靶量dMT关于目标和拦截弹的弹道参数表达式。
(6)

psin(Δ-σk)=sin(π-σT-Δ),
|Δ-σk|<π/2,p=V/VT
(7)
联立式(5)和(7)得到下面的约束条件
psinξ*=sin(π-σT-Δ)
(8)
1.4 虚拟目标的设置
联立并求解方程式(8),(2)和(5)可得视场角约束和零预测脱靶量约束下的方位角Δ,q0和终端弹道角σk,代入式(1)得虚拟目标的初始位置坐标。
基于虚拟目标初始位置,以及求得的σk,中制导律的设计和优化等价于一个具有弹道角约束的攻击匀速直线运动目标T′的问题。
2 导引律的设计
由图1可得拦截弹与虚拟目标的下述相对运动方程
(9)
(10)
η=σ-q
(11)
ηT′=π-σT′-q
(12)
(13)
其中VT′=VT,V,σT′=σT均为常量。
2.1 交会时的弹目视线角计算
拦截弹与虚拟目标交会时刻r=0,联立式(10)~(12),得交会时刻的弹目视线角qk满足下面的方程
psin(qk-σk)=sin(π-σT′-qk),
|qk-σk|<π/2
(14)
比较式(7)和(14)知,Δ和qk均可看作下面关于x的方程的2个解:
psin(x-σk)=sin(π-σT-x),
|x-σk|<π/2
(15)
由文献[4]中的Proposition 1知,上述方程有且仅有1个根,因此
qk=Δ
(16)
2.2 导引律优化
经典PPN抑制视线的旋转,
(17)
要使中制导末端视线旋转到期望视线角,其旋转角速率应为
(18)
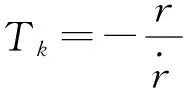
(19)

由式(11)和(12)可得
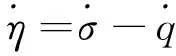
(20)
(21)
对式(10)微分,并将式(9),(10),(20)和(21)代入得
(22)
令
则得
用矩阵简明地表示为
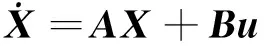

选择二次性能指标
(23)
由最优控制理论知最优控制
u*=-R-1BTPX
(24)

P-1(tk)=F-1=02×2
(25)
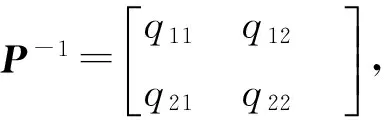
又因q12=q21,由上式得
(26)
(27)
(28)
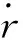

(29)
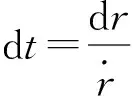
联系r(tk)=0,q12=0。对上式两边积分得
代入式(26)并积分得
则可得逆矩阵P-1,P为
代入式(24),得最优控制律
则导引律可以表示为
(30)
3 指令形成
综上所述,对于目标非机动的情形,形成控制指令的步骤如下:
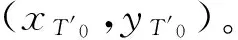

上述导引律同样适应于目标机动的情形。由于大气层内目标的机动大部分是长距离的微小机动,可将每个采样时段内的运动看作匀速直线运动,并将虚拟目标和初始条件的定义过程纳入在线计算,即在每个采样时刻,根据新测量的信号,执行一次步骤1)和2),定义新的虚拟目标和终端约束条件,通过式(30)获得相应的控制信号,依次循环。
4 仿真分析
假设在中制导开始时刻,拦截弹位置(xM0,yM0)=(40,10)km,v=2.04km/s,σ0=50°;实际目标位置(xT0,yT0)=(330,35)km,vt=1.7km/s;导引头探测距离L=60km,末制导视场角约束ξ∈(5°,27°)。则当目标航向角分别取σT=175°/185°的情况下,拦截弹与虚拟目标交会的弹道轨迹分别如图3和图4所示,目标偏离导引头视场中央的角度分别为0.05°/0.01°。仿真结果表明,拦截弹在针对虚拟目标的偏置比例导引律作用下,能够于中制导结束时,将实际目标准确地收入期望的导引头视场位置,并且瞬时脱靶量为0。

图3 目标航向角175°时的拦截弹道
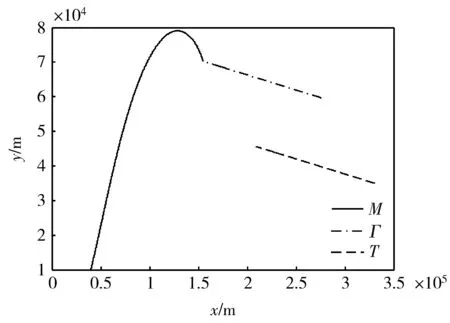
图4 目标航向角185°时的拦截弹道
5 结论
侧窗探测技术的采用和大气层的特点对该空域内拦截弹的中制导弹道提出了严格要求。本文从其特殊的终端视场角约束和预测脱靶量为0出发设置虚拟目标,将视场角约束转化为拦截虚拟目标时的弹道角及弹目视线角约束,继而对导引律进行优化设计。其中二次型性能指标的引入,尤其是带有无穷加权矩阵的终端惩罚函数项的引入保证了中制导末端视场角约束的精确满足,同时又使中制导末端时刻的瞬时视线转率为0,弹目相对运动方向稳定,为导引头在末制导过程中始终跟踪目标提供了保证。仿真结果表明本文所提出的方法可以精确满足中末制导交班要求,并为末制导弹道的平直性提供了保障。
参 考 文 献
[1] 宋明军, 魏明英.侧窗探测条件下的制导控制系统设计方法研究[J].现代防御技术, 2007, 35(5): 71-75.(SONG Mingjun, WEI Mingying.Control Guidance System Design Method for Side Window Detection[J].Modern Defence Technology, 2007, 35(5): 71-75.)
[2] 周艳萍, 张锐, 李君龙.侧窗探测下的姿态变结构控制[J].现代防御技术, 2006, 34(1): 29-32.(ZHOU Yanping, ZHANG Rui, LI Junlong.Attitude Variable Structure Control for Side Window Detection[J].Modern Defence Technology, 2006, 34(1): 29-32.)
[3] Murtaugh S A, Criel H E.Fundamentals of Proportional Navigation[J].IEEE Spectrum, 1966, 3:75-85.
[4] Kim B S, Lee J G, Han H S.Biased PNG Law for Impact with Angular Constraint[J].IEEE Transactions on Aerospace and Electronic Systems, 1998, 21(1): 277-288.

