高速铁路路基沉降预测编程实现及实例分析

刘文忠，戴华阳，王 强，肖先华，石新庄

（1.中国矿业大学（北京）地球科学与测绘工程学院，北京100083;2.重庆市勘测院，重庆400000）

一、引 言

高速铁路是现代化铁路的重要标志，集中体现了当代高新技术的发展成果，代表着当今世界铁路的发展方向［1］。随着铁路速度的提升，对铁路路基的稳定性要求也越来越高。高速铁路路基的稳定性需要达到相应的标准后才能铺轨，通过何种预测方法来预测高速铁路路基的稳定性，许多学者对此进行了研究［2-11］。主要沉降预测模型和方法有:灰色理论GM(1，1)模型、改进的指数预测模型、双曲线预测模型、Pearl预估模型、非等间隔的灰色 Verhulst模型、三点修正指数曲线模型、三点法、Asaoka法、拓展双曲线法、泊松曲线法和准固结法等。

二、沉降预测方法

本文选用拓展双曲线法、三点法和指数曲线法［1］3种高铁沉降预测方法，以VC++为开发工具，通过MFC编程实现了高铁路基沉降变形的预测。

1.拓展双曲线法

拓展双曲线法假设沉降量St随时间t的变化可描述为

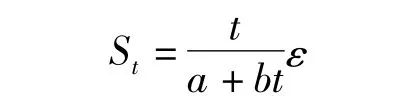
式中，t为自土方工程开工以来时间，单位为d;St为t时刻的沉降，单位为mm;σ为t时刻的荷载，单位为kPa;δmax为设计最大荷载，单位为 kPa;ε =δ/δmax。

2.三点法

三点法假定沉降量St随时间t的发展过程可描述为

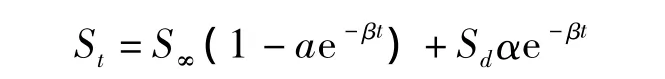
式中，Sd为瞬时沉降，单位为mm;S∞为最终沉降量，单位为mm;α、β为实测数据经过曲线回归求得的系数。

3.指数曲线法

实测沉降曲线自拐点B(t0，S0)开始，近似按指数曲线延伸，指数曲线方程可表示为

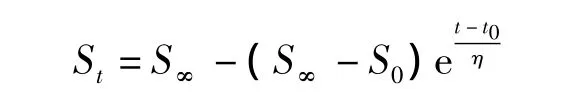
式中，St为t时刻的沉降;S∞为最终沉降量;S0为t0对应的沉降量;η为待定常数。

三、基于MFC沉降预测的编程实现

1.部分结构体和变量的定义

定义的结构体包括拓展双曲线法Para SQX、三点法ParaSDF、指数曲线法ParaZSQX、线性方程拟合结构体Para_AB，以及一个点一个时刻的载荷、时间、沉降量结构体PTS，一个点所有时刻的信息结构体Sediment-PtInfo等。以下是对SedimentPtInfo结构体的定义。

struct SedimentPtInfo

{CString m_strName;∥储存点名的变量

vector＜PTS＞m_vSrc;∥储存观测数据的变量

vector＜CString＞m_vStrPreTime;∥储存拟合时间的变量

ParaSQX m_paraSqx;

ParaSDF m_paraSdf;

ParaZSQX m_paraZsqx;

…

int m_tStart;∥储存土方工程开工时间(天)

};

vector＜SedimentPtInfo＞m_vPtAll;∥储存所有点信息的变量

2.文件的读取与方程参数的求取

1)文件的读取。

2)方程参数的求解。

∥通过观察值x，y，调用Calc_ab函数求直线y=a+bx的参数a和b，调用时需把拓展双曲线方程和指数曲线法方程转换成线性形式_vSrc，m_vPtAll［i］.m_vSrc.size()，m_vPtAll［i］.m_tStart);∥CalcParaSqx函数通过调用Calc_ab函数计算出相关参数，进而求得拓展双曲线法方程的参数，并存于m_paraSqx结构体中。

m_vPtAll［i］.m_paraSdf=CalcParaSdf(m_vPtAll［i］.m_vSrc，m_vPtAll［i］.m_vSrc.size()，m_vPtAll［i］.m_tStart);

∥调用CalcParaSdf函数计算三点法方程的参数，并存于m_paraSdf结构体中。

m_vPtAll［i］.m_paraZsqx=CalcParaZsqx(m_vPtAll［i］.m_vSrc，m_vPtAll［i］.m_vSrc.size()，0.4);∥ CalcParaZsqx函数通过调用函数Calc_ab计算出相关参数，进而求得指数曲线法方程的参数，并存于m_paraZsqx结构体中。

3.曲线拟合

新建哈大客专线哈尔滨西客运站工程Ⅱ标段参评路基长度2 186.65 m，设计时速350 km/h，为有砟轨道。本段路基经过地貌单元为松辽平原北部岗阜状冲积平原区。路基小里程前段地势较低，逐渐进入城镇后地势趋于平缓。工点范围地形相对较平坦、狭长，房屋密布，工点区出露地质主要为第四系全新统人工填筑土、上更新统冲积黏质黄土、粉质黏土，底层则为砂土层。

1)以Ⅱ标段DK919+950观测断面为例，分别采用拓展双曲线法、三点法和指数曲线法对该断面的实测数据进行了拟合，如图1～图3所示。其中，点曲线表示实测曲线;光滑曲线表示拟合曲线;直线表示最终沉降量;横轴表示时间;纵轴表示累计下沉量。

2)由拓展双曲线法计算出的相关系数为0.997，最终沉降预测值为1.84 mm，工后沉降为0.65 mm;由三点法计算出的相关系数为0.995，最终沉降预测值为1.17 mm，工后沉降为0.25 mm;由指数曲线法计算出的相关系数为0.994，最终沉降预测值为1.33 mm，工后沉降为0.34 mm。

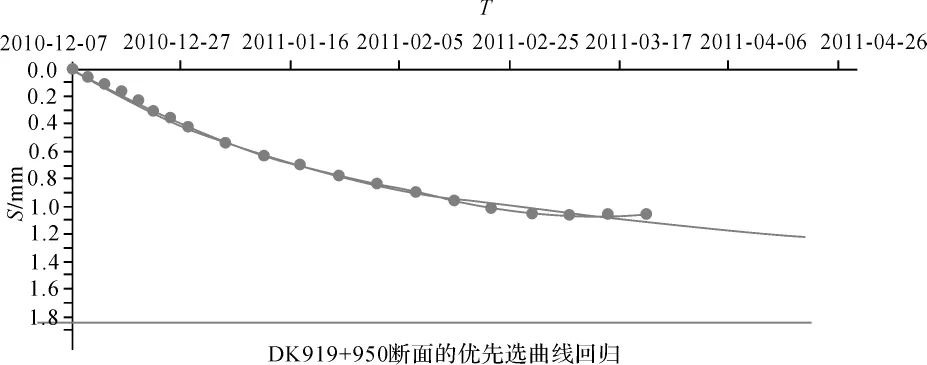
图1 DK919+950断面的优选曲线回归(拓展双曲线法)

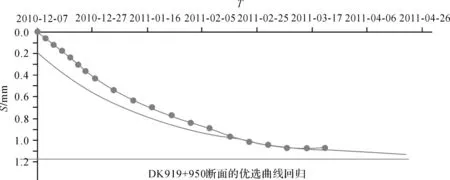
图2 DK919+950断面的优选曲线回归(三点法)

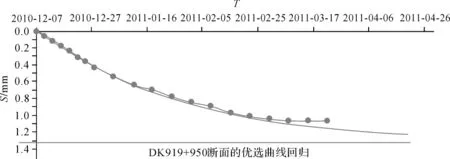
图3 DK919+950断面的优选曲线回归(指数曲线法)

3)对比分析。由相关系数分析可知，拓展双曲线法、三点法和指数曲线法拟合精度依次为0.997、0.995、0.994，表明拓展双曲线法适合用来预测DK919+950观测断面路基沉降变形;而根据工后沉降预测结果可知，DK919+950观测断面工后沉降满足设计要求。

四、结 论

1)依据间接平差法原理和利用MFC单文档，可以分别编程实现了线性参数的求取和高效设计用户交互式界面及完成图形的显示。

2)本文采用拓展双曲线法、三点法和指数曲线法对Ⅱ标段DK919+950观测断面的实测数据进行了拟合，分别求得相关系数。3种曲线拟合法的拟合精度依次为0.997、0.995、0.994，表明拓展双曲线法适合用来预测DK919+950观测断面路基沉降变形。

3)通过对新建哈尔滨西客站工程Ⅱ标段DK919+950观测断面工后沉降预测，得出该观测断面工后沉降小于有砟轨道路基工后沉降容许值50 mm和无砟轨道路基工后沉降容许值15 mm，满足设计要求。

［1］ 陈善雄，宋剑，周全能，等.高速铁路沉降变形观测评估理论与实践［M］.北京:中国铁道出版社，2010:134-137.

［2］ 冯震，阎文发，姚海波，等.路基沉降的灰色理论预测及实例验证［J］.华北科技学院学报，2003，5(3):23-25.

［3］ 辜清华，何良德.预测路基沉降的一种新模型［J］.石家庄铁道学院学报，2006，19(2):64-67.

［4］ 陈凯.双曲线法在路基沉降变形预测中的应用分析［J］.工程建设与设计，2009(10):83-85.

［5］ 郭亚宇，郭昕，庞旭卿，等.Pearl模型在高速铁路路基沉降预测中的应用［J］.土工基础，2010，24(4):44-46.

［6］ 明祖涛，游振兴，张届，等.高速铁路桥隧沉降预测模型的研究［J］. 测绘通报，2011(8):17-19，41.

［7］ 王小刚，陈善雄，余飞，等.拓展双曲线法在铁路客运专线路基沉降预测中的应用［J］.铁道标准设计，2010(2):39-42.

［8］ 于春海，陶福金，杨有海.郑西客运专线试验段路基沉降变形预测［J］.路基工程，2010(1):77-78.

［9］ 肖霞林.路基沉降变形评估与非等间隔灰色 Verhulst模型［J］.铁道建筑，2011(4):86-88.

［10］ 陈善雄，王星运，许锡昌，等.秦尚林路基沉降预测的三点修正指数曲线法［J］.岩土力学，2011，32(11):3355-3360.