基于某型号飞控半实物仿真试验变加载模拟技术的研究
董文彬 张宏伟 吴 骁 周 展
北京航天自动控制研究所,北京 100854
在航天型号的仿真试验中,由于舵机系统特性随负载力矩变化,很难对其建立准确的数学模型,因此在仿真试验中必须采用真实的舵机系统。而在地面半实物仿真试验中,大多数试验室没有风洞,无法模拟由于风力变化引起的作用在舵面上的舵机系统负载力矩变化,因此在传统试验中,使用钢板加载的方式对舵机系统进行力矩加载。传统的钢板加载为线性加载,梯度恒定,加载力矩和钢板的扭转角度成线性关系。而真实的舵轴受力情况和舵轴的扭转角度并不是严格呈线性正比关系的,为了更加真实地模拟舵机系统在真实飞行时的受载情况,需要通过变加载模拟系统完成[1]。
变加载系统是以力(矩)为被调整量的电液伺服系统[2-4],根据承载对象的运动规律又可分为以下2类:主动式加载系统,承载对象不主动运动,它的运动是因为加载系统的加载力(矩)引起的,这种加载试验对于加载系统来说又称为静态加载;被动式加载伺服系统,承载对象主动运动,加载系统在跟随其运动的同时进行加载,这种加载又称为动态加载。本文的变加载系统是一个典型的被动式电液力(矩)伺服加载系统,舵机和负载模拟器是相互作用相互影响的[5],系统组成如图1所示。左边是承载对象,右边是加载系统。
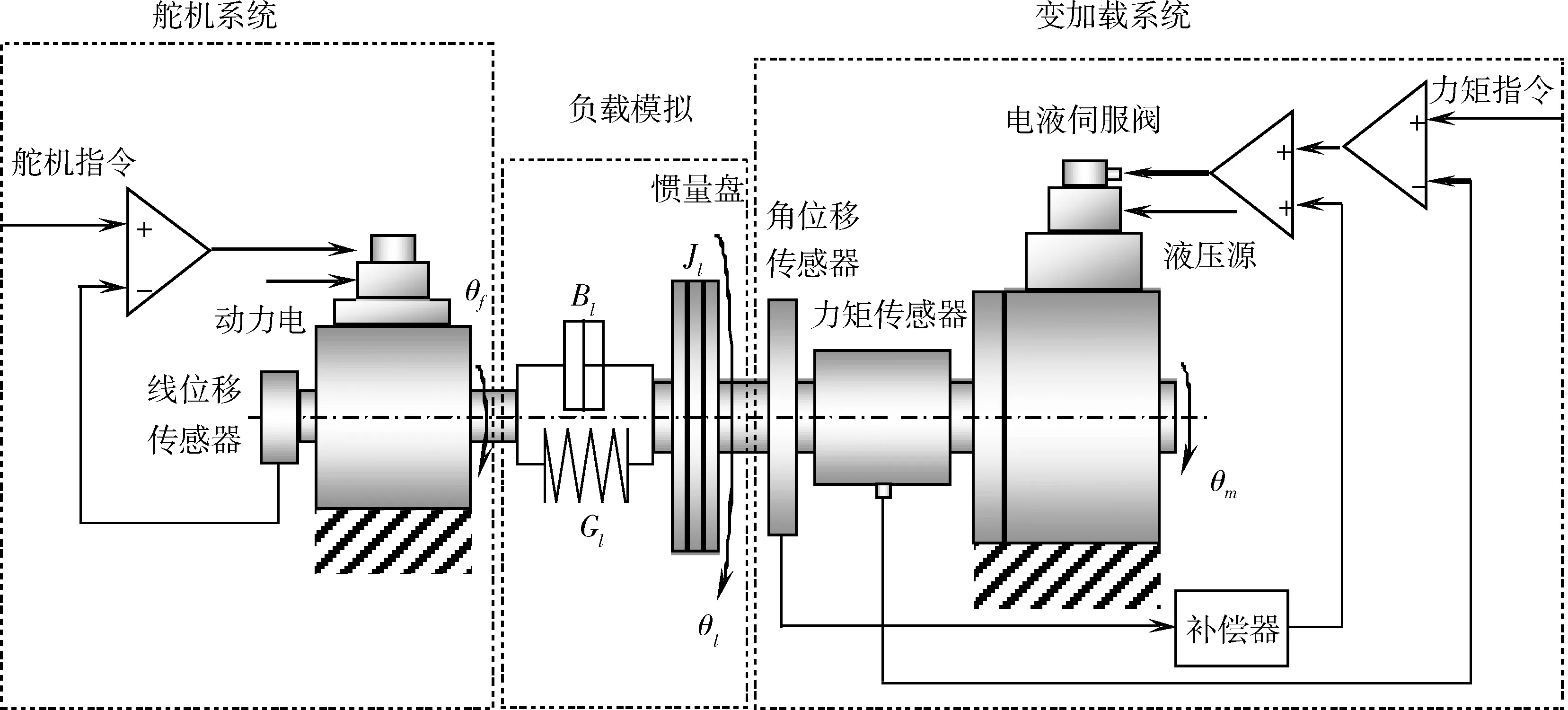
图1 变加载仿真系统示意图
1 试验系统组成
本文研究的变负载模拟系统是基于某飞行型号来设计的,仿真试验原理框图见图2。
在加上变负载之后的闭环试验中,地面仿真计算机通过A/D接口板采样舵机输出的摆角信号,进行控制力、气动力和箭体运动方程等模型计算。计算完成后将模型输出的视速度增量和角度增量信号送给惯组模拟器,惯组模拟器通过并口上传给控制组合。控制组合获得飞行器当前的角度、视速度数据后,由飞行软件进行姿态、弹道参数迭代计算,导引计算和控制信号解算,形成舵机的动作指令,舵机指令下传给舵机控制器,舵机控制器根据指令利用功放驱动电动舵机带动变负载装置转动,模拟飞行状态的摆角输出。同时,地面仿真机将计算好的负载力矩指令传给变负载模拟器对舵机进行加载,电动舵机再通过固连在输出轴上的角电位器反馈输出摆角电压信号,送给地面仿真计算机内的A/D采样板,完成系统的闭环仿真。试验系统的照片如图3所示。
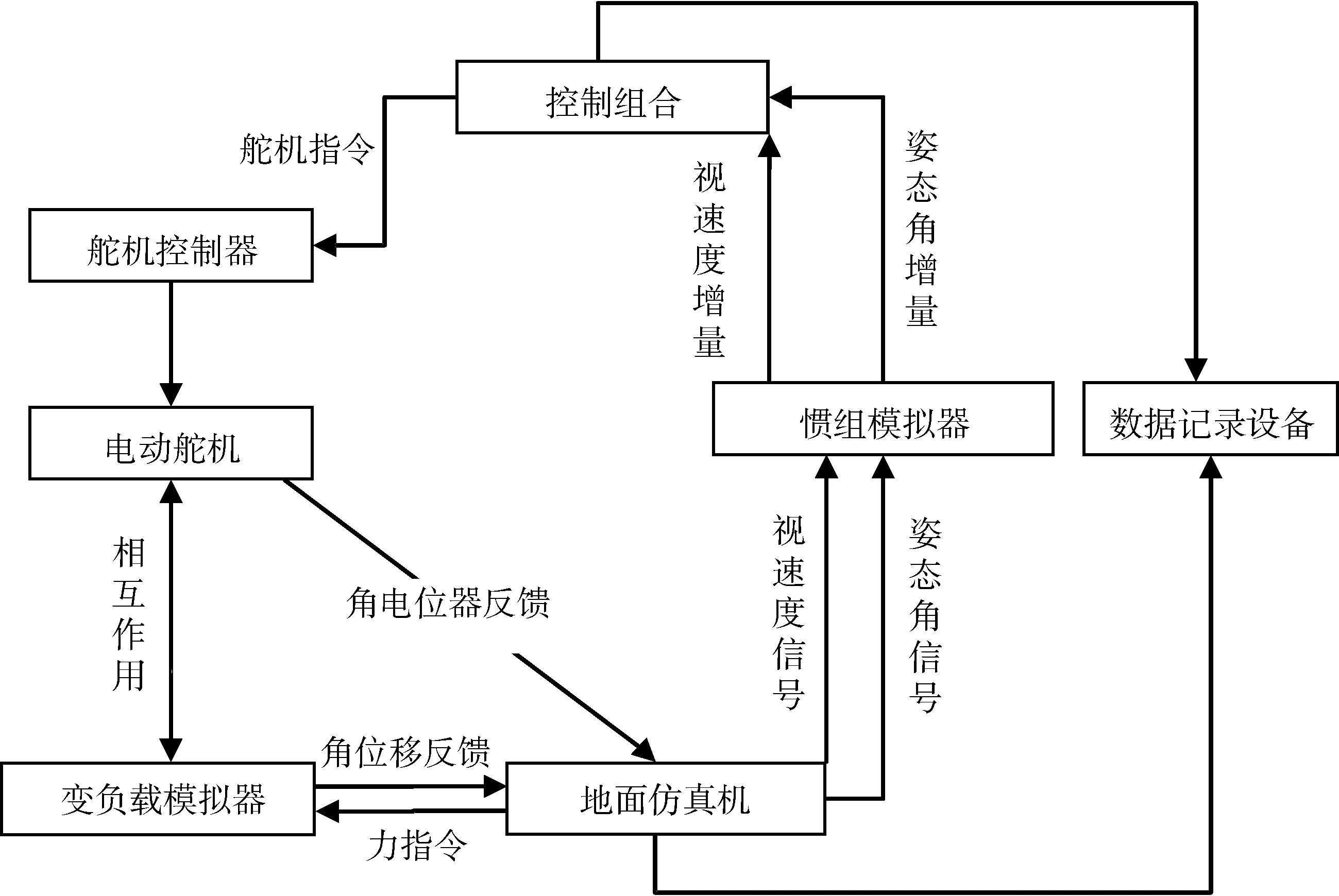
图2 使用了变负载模拟器的半实物仿真试验原理图

图3 基于某飞行型号的变加载模拟试验系统
2 加载试验分析
下面通过2种试验对变加载系统进行研究。
(1)梯度试验
传统试验中,模拟力矩使用的是负载钢板,加载为线性正梯度力矩,力矩作用为单一的阻碍舵面转动,梯度唯一且不能够实现反向加载。在本文中,先将负载模拟器当做负载钢板使用,使其加载线性力矩。试验中计算机经角位移传感器采集角位移信号,进而根据设定好的梯度值计算出加载指令,计算时使加载梯度分别为0(不加载,加载轴随着舵轴转动),1,2,-1(反向加载,作用为帮助加载轴转动),-2。通过运行同一条真实弹道,研究加载模拟器代替可变梯度钢板的力矩加载追踪效果。
从图4~8中可以看到,在运行真实弹道、不同加载梯度的试验环境下,负载模拟器都可以较为准确的模拟出所需加载力矩,以代替不同加载梯度的钢板作用。由此可见,负载模拟器可以实现不同线性梯度加载的功能。

图4 梯度为0时加载效果
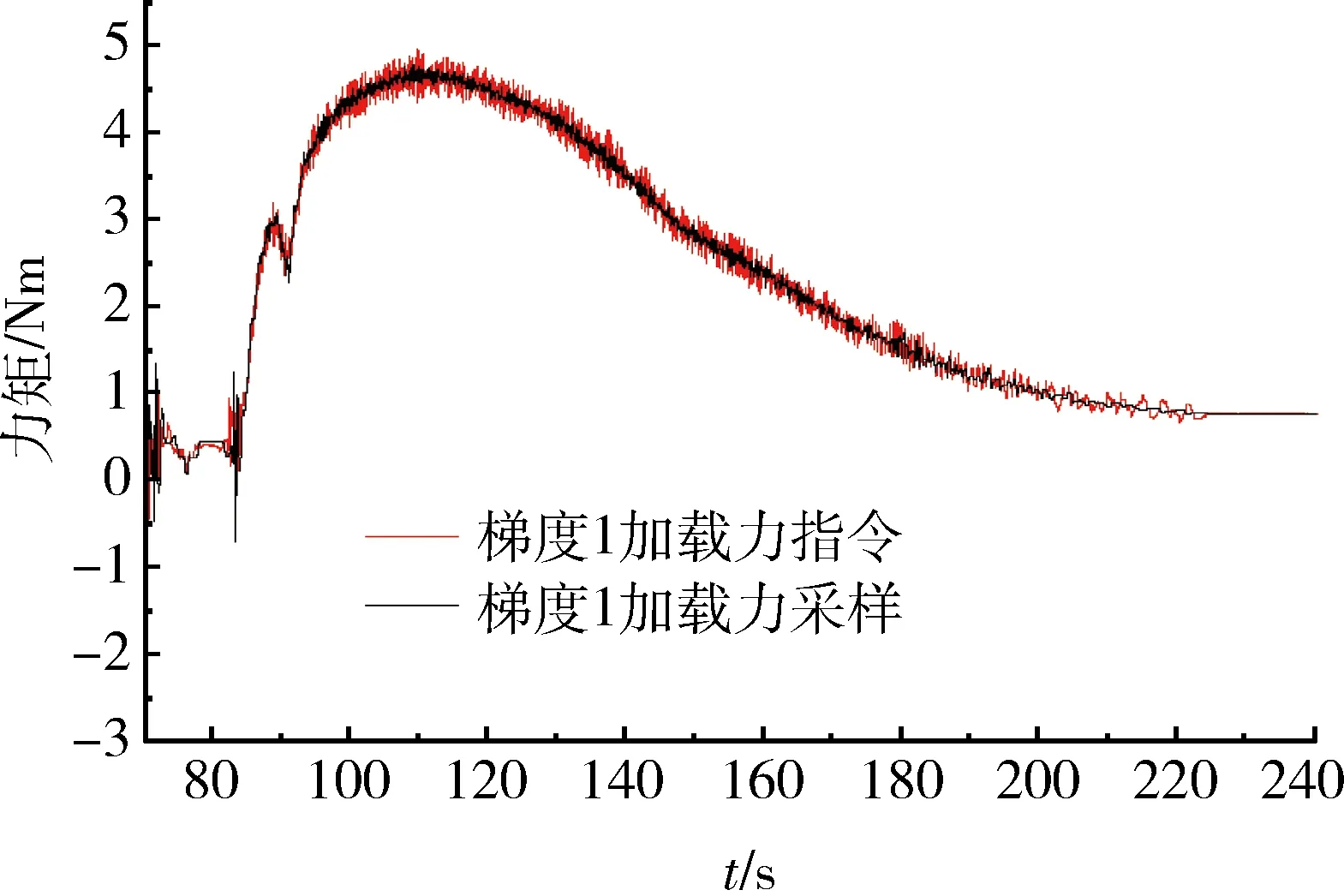
图5 梯度为1时加载效果

图6 梯度为2时加载效果

图7 梯度为-1时加载效果

图8 梯度为-2时加载效果
(2)实时加载试验
此试验中仿真机通过解算出的姿态角,根据受力力矩公式计算出加载力矩,在给惯组模拟器发送指令的同时将力指令传送给变加载系统,由变加载系统对舵轴进行实时加载,加载曲线见图9。

图9 实时加载试验时加载效果
可见负载模拟器在实时加载中可以很好的复现实时力指令。
3 加载影响分析
将传统试验时采用钢板加载时的曲线和同弹道采用实时加载时的曲线进行对比,将它们的同一舵机的线位移传感器采样放在一起分析实时加载相比传统钢板加载对舵机线位移的影响(线位移传感器装在舵机内),见图10。

图10 真实加载时和钢板加载时线位移比较
由图10可见,采用实时加载时舵机系统的线位移曲线和采用钢板时线位移的曲线重合度较好,可以说明负载模拟器在做真实加载时相比钢板加载对舵机线位移的影响不大,负载模拟器的可变加载在半实物仿真试验中应用是可行的。
将钢板加载时的线位移,梯度0加载(空载)时的角位移,梯度1和2加载时的角位移进行对比,如图11所示。

图11 不同加载梯度对舵机角位移影响
由图11可见,在空载时,角位移和钢板加载时的线位移变化不大。在进行加载之后,角位移的幅值有明显的降低,而对动态特性的影响不大。由于角位移传感器通过机械连接装置安装在舵轴的外方,正加载力矩的作用效果为阻止舵轴转动,因此可以推断出由于加载力的阻碍影响引起了连接装置的形变,使得角位移传感器输出相比线位移传感器输出被“吃”掉了一个角度,且随着加载力矩的增大,引起的形变也更大。
将钢板加载时的线位移,梯度0加载(空载)时的角位移,梯度-1,-2加载时的角位移进行对比,如图12所示。
由图12可见,负加载梯度加载时,角位移的变化没有正加载梯度变化时明显,因为负梯度加载力矩的作用是助推舵机转动,使得连接装置的变形并没有正加载时的变形大,从而使得角位移变化相对较小。
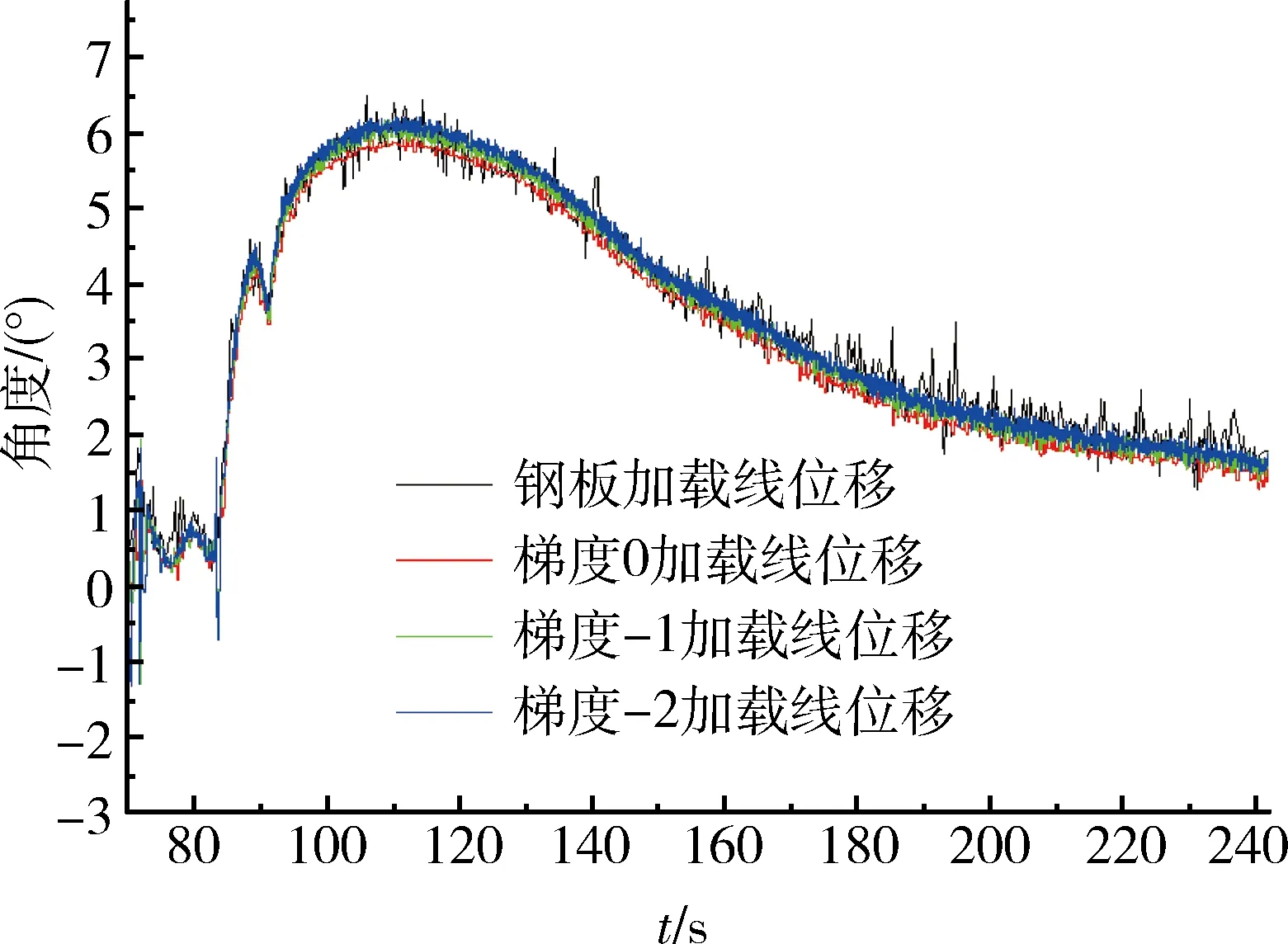
图12 负加载梯度对角位移影响
4 结论
本文采用某型号的实物系统,用不同的加载形式、模拟真实飞行弹道进行了试验。针对负载模拟器的加载情况和舵机的线位移、角位移输出比对进行了研究,得到如下结论:
1)对于采用扭转形式的舵机系统来说,采用变负载模拟器可以代替传统的钢板加载,且加载梯度可变,这对于摸索不同加载极限条件下的舵机性能指标是有帮助的,且具有对扭转形式舵机加载通用化的应用潜力。变负载模拟器可以很好地跟踪仿真机实时计算出的力指令,真正实现了传统钢板加载不能做到的非线性可变加载。
2)实时变加载时舵机的线位移输出相比传统钢板加载的线位移输出变化不大,此线位移在并入仿真回路后,系统控制仿真结果和在传统钢板加载下的仿真结果基本一致。可知在使用实时变加载时,舵机系统和控制系统并无发散,能够正常运行,因此变负载模拟器的实时可变加载在控制系统中的应用是可行的。
3)在对不同加载情况下,将舵机线位移输出和角位移输出对比后可知,由于角位移装在舵机转轴外端,连接装置的变形导致在有正向加载力矩时角位移输出幅值下降明显。而在进行反向力矩加载时舵机角位移幅值变化较小。由于在飞行中舵面的角度变化也是在舵轴输出轴外端,角位移(包含形变)可以反映更加真实的飞行情况,此研究给测量飞控系统外端舵面的真实角位移情况提供了一种试验手段,对其进一步的研究具有参考意义。
[1] 汪首坤,等.导弹舵机动态加载技术[J].北京理工大学学报,2007,3:44-45.
[2] 华清,等.电液负载模拟器的精确数学模型[J].机械工程学报,2002,38(11):31-35.
[3] 张晓旭.电液负载仿真台数学模型及动态特性的研究[D].沈阳工业大学硕士学位论文,2005.
[4] 刘长年.液压伺服系统优化设计理论[M].冶金工业出版社,1989,8.
[5] 焦宗夏,等.电液负载模拟器的复合控制[J].机械工程学报,2002,12:78-80.

