基于协同裕度的多飞行器航迹规划*

汲万峰 王光源 章尧卿 李伟波

海军航空工程学院，烟台 264001

在未来战争中，随着敌方综合防御体系的日趋完善，作战飞行器在突防过程中面临的威胁日益增加，单飞行器单独完成作战任务的难度不断增大，因此，常需要组织飞行器编队对目标实施协同攻击。为了充分发挥协同作战的优势，需要进行多飞行器协同航迹规划，通过飞行航迹的协同与配合，达到相比单机更优的战术效果[1]。

多飞行器协同执行作战任务，经过预规划后，各飞行器沿着各自的航迹飞行。但现代战争条件下，战场形势复杂多变，飞行环境、威胁分布的改变可能导致预规划的航迹效率降低甚至不可行。因此，在多飞行器协同航迹规划中，提高航迹应对环境变化的能力非常必要。传统的多飞行器协同航迹规划[2-9]，在处理飞行环境的突发性变化问题时，并没有对协同策略本身做出改进，单纯以航迹代价最小化为优化目标，得到的协同航迹适应环境变化的能力相对较差。

鉴于此，本文提出多飞行器航迹规划协同裕度的概念，建立了协同裕度模型，采用基于协同裕度的协同航迹规划方法。

1 多飞行器协同航迹规划基本模型

文献[10]构建了单飞行器航迹规划目标函数模型，见式(1)

(1)

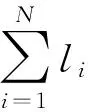
多飞行器协同航迹规划，还要考虑以下约束条件：

1)时间协同约束：设N架飞行器的到达目标的时间分别为T1,T2,…,TN，那么对于第i架飞行器，必须满足如下表达式：

|Ti-T1|≤ΔT,|Ti-T2|≤ΔT,…,|Ti-Ti-1|≤ΔT,

|Ti-Ti+1|≤ΔT,…,|Ti-TN|≤ΔT

其中ΔT为要求的到达目标的最大时间间隔。用Δti表示第i架飞行器与其它飞行器同时到达目标的时间协同代价，将其作为代价因子加入到代价函数中，Δti计算如下：

Δti=max(|Ti-T1|,|Ti-T2|,…,|Ti-Ti-1|,

|Ti-Ti+1|,…,|Ti-TN|)

(2)

2)安全无碰撞约束：对于K架飞行器，以飞行器间的距离代价作为避免发生碰撞的约束因子。方法是从飞行器起始点开始用一个时间增量对航迹进行采样，计算出每条航迹上当前时刻节点的坐标，通过坐标就可以计算出在当前时刻各个飞行器之间的距离，将这个距离作为代价因子加入到代价函数中。以第i架飞行器为例，设ΔLi表示飞行器i与编队内其它飞行器之间的安全距离代价，ΔLi的计算公式为：

(3)

式(3)中，Lij表示第i架和第j架飞行器在某同一时刻所处位置之间的距离，Dsafe为规定的安全距离。在同一时刻飞行器之间的距离在Dsafe以内就认为可能会发生碰撞。

根据以上分析，对于协同航迹规划中的单条航迹i，其约束函数计算如下：

Pi=α1Pf+α2ΔLi+α3Δti

(4)

式(4)中，Pf的含义同式(1)，表示单飞行器规划约束条件，α1,α2,α3表示权重系数。

根据式(1)表示的单飞行器航迹规划目标函数模型，可得多飞行器协同航迹规划第i条航迹的目标函数模型为：

Wi=αwdi+(1-α)wti+Pi

(5)

式(5)中，wdi为航迹i的航程代价，wti为航迹i的威胁代价。因此，多飞行器航迹规划目标函数模型为：

(6)

式(6)中，K表示飞行器架数。

2 基于协同裕度的多飞行器航迹规划模型

多飞行器协同航迹规划根据飞行器起飞时间是否一致可以分为同时出发和依次序出发2种情况。下列情况需要同时出发：1)为了统一指挥的方便和需要；2)在多飞行器多任务规划时，飞行器在执行完部分任务后，协同执行另一项任务。飞行器依次序出发情况下的协同航迹规划比较简单，本文重点研究同时出发情况下的协同航迹规划。

2.1 协同裕度涵义

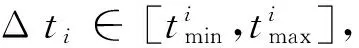
(7)

其中N为飞行器数量。如果S≠Φ，可以选一个协同时间t∈S，各飞行器根据协同时间t计算出各自的速度，分别以相应速度飞行，达到协同的目的；如果S=Φ，则说明各飞行器航迹长度差别太大，在飞行器的速度调整范围内不能达到时间协同的目的，这就需要对航迹长度较短的飞行器进行航迹重规划，使其航迹长度增大，直到S≠Φ，满足飞行器编队的整体协同。

飞行器编队在飞行过程中，由于作战环境和威胁分布的变化而需要进行重规划时，通常为了规避突发威胁而使得航迹长度增大，而导致飞行器按照预定的速度飞行或沿着预定航迹飞行时不能在预定的协同时间t内到达目标点，因而需要提高速度或重新规划后续航迹而推迟协同时间，以达到重新协同的目的。因各飞行器的速度都有一个变化范围，较理想的情况有以下2种：1)当某一飞行器因规避突发威胁而增大了航程时，通过提高飞行速度就可以按时到达目标点而不需要推迟协同时间；2)当该飞行器在其飞行速度范围内通过提高自身速度也不能在预定的协同时间到达目标点，整体协同时间需要推迟，但其它飞行器不需要进行航迹重规划，仅通过调整各自飞行速度就可达到重新协同的目的。上述2种情况在最大程度上减少了航迹重规划的次数或需要重规划航迹的飞行器的数量，从而减少了各飞行器因航迹重规划而频繁进行的通信交流，节省了通信和计算资源。

根据以上分析，将飞行器编队执行任务过程中，规避突发威胁时仅通过速度调整就可达到时间协同的能力称为协同裕度。

2.2 基于协同裕度的航迹规划模型

2.2.1 第一种情形

式(7)中，当S≠Φ时，为使飞行器编队代价函数最小，通常取t=min(S)作为协同时间，因而飞行过程中，航迹最长的飞行器(称其为飞行器甲)以最大速度vmax飞行，其它飞行器以低于vmax的一定速度飞行。这样在飞行过程中，当飞行器甲因遭遇突发威胁进行规避而增大了航程时，就不能通过调整速度而在t时间到达目标点。因此可采取以下策略：计算出最小协同时间t后，可将t适当增大，这样飞行器甲就以一个较vmax小的速度飞行，当其规避突发威胁时，就可能通过提高速度飞行而不会影响协同时间，从而减少其他飞行器进行航迹调整的概率。这样虽然引起整个编队的代价函数增大，但编队适应环境变化的能力变强了。

针对此情况，以飞行器甲为基准进行协同。设其预定航迹长度为l，预定速度为v，预定协同时间为t。在其飞行距离为l1、已飞时间t1=l1/v时遭遇突发威胁进行规避，重规划后航迹距离增加值为Δl，则其还需要飞行的距离l′=l+Δl-vt1，设后续航迹的飞行速度为v′，则所需时间t2=l′/v′，如果t2≤t-t1，则飞行器甲仅通过速度调整就可在预定的协同时间到达目标点，其它飞行器不需要作出调整。设Δv=v′-v，考察t2=l′/v′=l′/(v+Δv)，在l′的值一定的情况下，显然当Δv越大时，t2的值越小，通过提高速度达到协同的概率就越大，但因飞行器有一个速度变化范围[vmin,vmax]，因而Δvmax=vmax-v，由此可见，当飞行器的初始速度v越小，速度调整的范围越大，能够通过速度调整达到预定协同目的的概率越大。同时该飞行器初始速度v的减小也会带来编队其它飞行器速度的减小。将Δvimax=vimax-vi称为此种情况下飞行器i的协同裕度，其中，vimax表示飞行器i的最大速度，vi表示飞行器i的预定速度。Δvimax的值越大，协同裕度越大。但另一方面，当Δvimax增大时，可能导致协同时间增大，进而造成各飞行器编队的航迹代价增大，因而Δvimax和航迹的代价函数是一个相互制约、相互矛盾的关系，需要根据战场态势和作战任务综合衡量。该情况下，建立多飞行器航迹协同的目标函数模型为

(8)

其中β为权重系数。

2.2.2 第二种情形

式(7)中，取t=min(S)作为编队协同时间，飞行器甲以vmax速度飞行，其它飞行器以低于vmax的一定速度飞行。当各飞行器航迹长度差别较大时，航迹长度较短的飞行器(称其为飞行器乙)就可能以接近vmin的速度飞行。这样当飞行器甲因规避突发威胁而引起编队协同时间推迟时，飞行器乙因速度减小的余地有限，就不能通过降低速度达到时间协同。因此可采取以下策略：航迹预规划时，航迹较短的飞行器适当延长航迹距离。这样在飞行器甲因规避突发威胁而引起编队协同时间推迟时，其它飞行器就可能通过调整速度达到重新协同的目的，而不需要进行航迹重规划。

针对此情况，考虑这样一种极限情形，如图1所示。图中A飞行器的航线航程为899km，而B飞行器的航线航程仅为795km，两者相差104km。在这种情况下，各飞行器飞行速度差别很大，才能达到协同目的。图1中，预定协同时间t=68min，飞行器速度变化范围v∈[680,800]，求得A飞行器的飞行速度为793km/h，接近飞行器的最大速度，而B飞行器的飞行速度为701km/h，接近飞行器的最小速度。该情况下，当飞行器A在飞行过程中某时刻1遭遇突发威胁而需要规避时，因速度调整的幅度有限，其到达目标的时间必将向后推迟一个时间段Δt，从而整个飞行器编队的协同时间也将向后推迟一个时间Δt。该情况下B飞行器速度调整的幅度同样有限，因而其必须重规划，以一个较大航程的航线飞行，才能达到协同的目的。这种情况下飞行器编队的协同裕度显然较低。

图1 多飞行器协同航迹规划示意图

图1中，A，B飞行器沿着预规划航迹飞行，A飞行器在飞行过程中发现一突发威胁，以前方M点作为起始点进行重规划，此时已飞行225km，重规划后航迹长度增加31km，协同时间推迟3min。B飞行器以前方N点作为起始点进行重规划，此时已飞行144km，重规划后航迹长度增加了30km。

针对上述情形，首先考察多飞行器预规划协同航迹，各航迹长度为l1,l2,…,lN，各飞行器速度为v1,v2,…,vN，则：

(9)

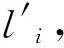
(10)

其中γ为权重系数。

图2中，采用模型(10)的方法，B飞行器航线距离853km，A飞行器规避威胁后，B飞行器不用重规划，以速度720km/h飞行就可，协同时间为71min。通过在预规划中适当增加B飞行器的航迹长度，增加了编队的协同裕度，提高了协同能力。

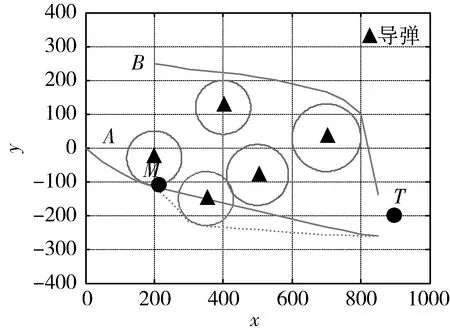
图2 多飞行器协同航迹规划示意图

2.2.3 基于协同裕度的航迹规划模型

(11)

3 仿真算例

A，B，C三架同型飞行器执行一项协同突袭T目标的任务，在直角坐标系下，A飞行器初始位置为(0,0)，B飞行器初始位置为(200,250)，C飞行器初始位置为(400,400)，目标点T位置为(900,-200)。经过预先侦察，获取作战空间内分布有敌方四处导弹威胁兵力，各威胁源位置及威胁半径如表1所示。

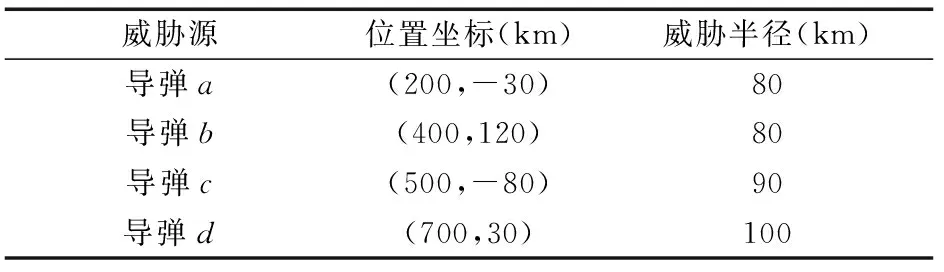
表1 威胁源分布

要求各飞行器避开敌方威胁，在同一时间对目标展开攻击。根据飞行器作战性能、目标属性特点及威胁分布情况，确定A，B，C三架飞行器的协同子目标点位置分别为(850,-140),(850,-260),(950,-140)，单位为km。已知A,B,C三架飞行器的速度变化范围为[680,800]，单位为km/h。

利用遗传算法进行航迹规划，种群规模大小为80，运算终止代数为300，在不同权重系数下规划得到的航迹结果如图3所示。

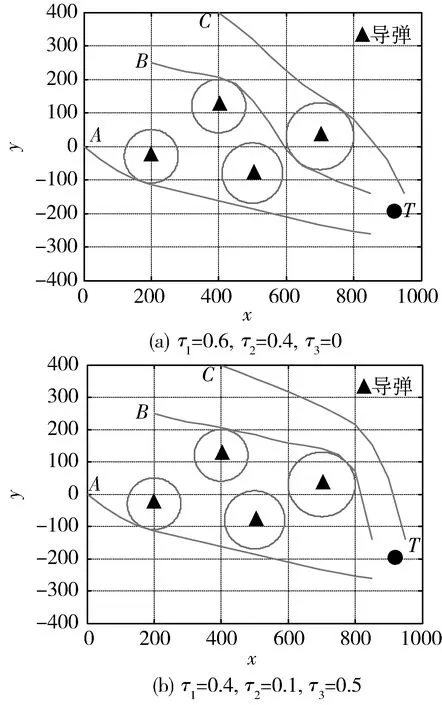
图3 多飞行器协同航迹规划示意图

图3(a)为协同裕度系数k3=0的仿真结果图，各飞行器规划出的是各自代价函数最小的航迹，编队协同时间68min。图3(b)为协同裕度系数k3=0.5的仿真结果图，各飞行器规划出的是综合考虑协同裕度的航迹，编队协同时间71min。表2为协同航迹规划仿真数据表。

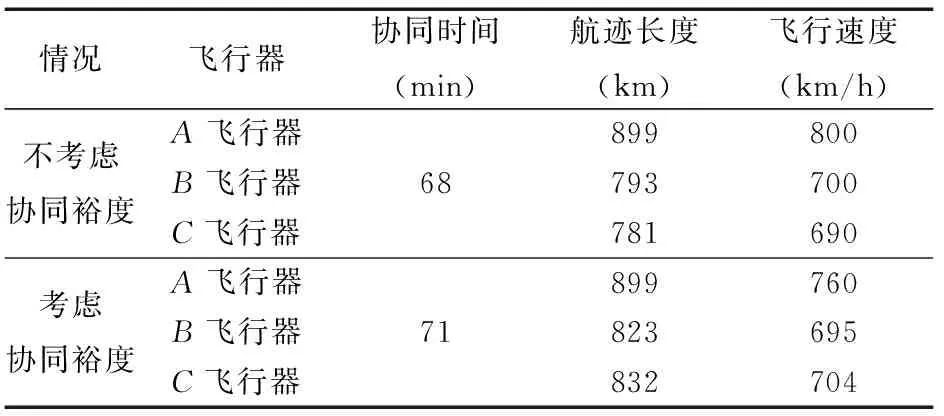
表2 协同航迹规划数据表

综合图3和表2可以得出：

1)考虑编队的协同裕度后，A飞行器以一个低于最大速度的航速飞行。这样在飞行过程中遇到突发威胁需要规避时，就可能通过提高飞行速度飞行而不耽误编队的协同时间。如假设A飞行器沿着预规划航迹飞行到M点时发现一突发威胁，中心坐标为(350,-150)，威胁半径为80km，以前方N点作为起始点进行航迹重规划。此时A飞行器已飞行了225km，飞行时间t1=17.8min。重规划结果如图4所示。

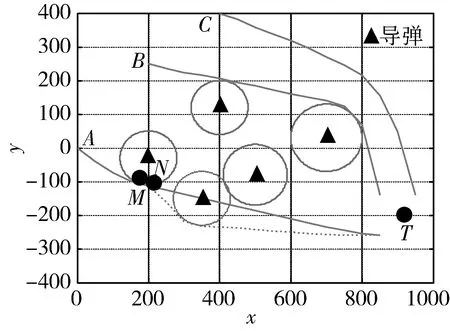
图4 多飞行器协同航迹重规划示意图

图4中，虚线表示的航迹为A飞行器的重规划航迹。在A飞行器的预规划航迹中，N点与子目标点间的航迹长度为674km，重规划后航迹长度增为705km，增加了31km。要能在预定协同时间到达目标点，经计算得A飞行器在后续飞行过程中的飞行速度v=798km/h，低于飞行器的最大速度。可见，A飞行器在后续过程中只需以798km/h的速度飞行，就能在预定协同时间到达目标点，整个飞行器编队的协同时间不需要推迟，因而编队中的B，C飞行器按照预定计划飞行就可，不需要调整。而当不考虑协同裕度时，A飞行器以最大速度800km/h飞行，当遇到突发威胁时，不能通过速度调整按预定协同时间到达目标，编队协同时间必须推迟一个时间段，从而B，C飞行器必须进行相应调整。

2)考虑协同裕度后，B，C飞行器的规划航迹降低了与A飞行器航迹长度的距离差，因而提高了各自的飞行速度。这样在A飞行器即使因为规避突发威胁而使得编队协同时间向后推迟时，B，C飞行器也可能通过降低本身的飞行速度就可达到协同，而不需要进行航迹重规划。如假设A飞行器沿着预规划航迹飞行到M点时突发威胁的中心坐标为(350,-150)，威胁半径为100km，以前方N点作为起始点进行重规划，规划结果如图5所示。

图5 多飞行器协同航迹重规划示意图

图5中，重规划后A飞行器的航迹长度为720km，增加了46km。A飞行器在后续过程中以最大速度800km/h飞行，则需要54min才能到达目标点，比预定协同时间推迟了1min。当A飞行器飞行了225km到达N点时，B飞行器飞行了206km，还剩余航程617km，C飞行器飞行了208.5km，还剩余航程623.5km。要使在重规划后的协同时间到达目标点，经计算可得B飞行器飞行速度为686km/h，C飞行器飞行速度为693km/h，均在飞行器的速度变化范围内。因此2架飞行器均可通过调整速度达到重新协同的目的，不需要进行航迹重规划。

4 结束语

本文研究了基于协同裕度的多飞行器协同航迹规划问题，建立了基于协同裕度的航迹规划模型，并通过仿真算例进行了验证。仿真结果表明：考虑协同裕度后，规划的协同航迹对环境变化具有更好的适应性。

[1] 严平.无人飞行器航迹规划与任务分配方法研究[D].武汉:华中科技大学,2006.(YAN P. Research on UAV Path Planning and Task Allocation Method[D].Wuhan: Huazhong University of Science and Technology,2006.)

[2] McLain T,Chandler P,Pachter M.A Decomposition Strategy for Optimal Coordination of Unmanned Air Vehicles[C].Proc.of American Control Conference,Chicago,2000: 369-373.

[3] T.McLain,R.Beard.Trajectory Planning for Coordinated Rendezvous of Unmanned Air Vehicles[C].Proceedings of the AIAA Guidance,Navigation,and Control Conference, Denver, Colorado,2000.

[4] Gokham Inalham,Stipanovic Dusan M,Tomlin Claire J.Decentralized Optimization with Application to Multiple Aircraft Coordination[C].Proc.of the 41st IEEE Conference on Decision and Control,Las Vegas,2002.

[5] 宋绍梅,张克,关世义.基于层次分解策略的无人机多机协同航线规划方法研究[J].战术导弹技术，2004,(1):44-48.(SONG S M,ZHANG K,GUAN S Y.Research on UAVs Cooperative Route Planning Method Based on Hierarchical Decomposition Strategy [J].Tactical Missile Technology, 2004,(1):44-48.)

[6] YANG Y,MINAI A A, POLYCARPOU M M.Decentralized Cooperative Search by Networked UAVs in an Uncertain Environment[C].Proceedings of the 2004 American Control Conference, 2004:5558-5563.

[7] Eun Y,Bang H.Cooperative Control of Multiple Unmanned Aerial Vehicles Using the Potential Field Theory[J].Journal of Aircraft,2006,43(6):1805-1814.

[8] 周炜,魏瑞轩,董志兴.基于层次分解策略无人机编队避障方法[J].系统工程与电子技术,2009, 31(5):1152-1157.(ZHOU W,WEI R X,DONG Z X.The Method of Obstacle Avoidance Strategy of UAV Formation Based on Hierarchical Decomposition Strategy[J].Systems Engineering and Electronics, 2009, 31(5):1152-1157.)

[9] 秦硕,朱凡,刘永学.多UAV协同路径规划研究[J].系统仿真学报,2008,20(23):6356-6358.(QIN S,ZHU F,LIU Y X.Research on Path Planning of Multiple Cooperative UAV[J].Journal of System Simulation,2008,20(23):6356-6358.)

[10] 汲万峰,姜礼平,朱建冲,阮冰.基于遗传算法的航路规划模型研究[J].军事运筹与系统工程,2010,24(2):52-55.(JI W F,JIANG L P,ZHU J C,RUAN B.Route Planning Model Based on Genetic Algorithm[J].Military Operations Research and Systems Engineering, 2010,24(2):52-55.)