A-φ方法在高频电磁场计算中的应用

逯贵祯，陈涛，邬丽云，康彤

(1.中国传媒大学信息工程学院，北京100024；2.中国传媒大学理学院，北京100024.)

1 引言

有限元方法早期在电磁场应用中，由于电磁场在不同媒质交界面处切向分量连续而法向分量间断的特性，基于节点的基函数不能有效处理非均于介质问题，并且存在非物理解的问题[1-2]，因此早期大量研究是如何克服这些电磁学中特有的有限元求解问题。对于这两个问题的研究大致分为两类，一类是针对节点基函数的问题，提出新的基函数，包括基于棱边的矢量有限元方法[3]。另一类是改变有限元的泛函表达式，包括使用不同的空间函数处理电磁场问题[1，4-6]。在离散单元的基函数研究中，基于棱边的矢量基函数被认为可以很好地克服上述所提到的问题，也是目前计算电磁学中有限元的主流方法[2]。但是，基于棱边单元的有限元方法需要对棱边单元进行特殊的编号处理，而目前大部分网格处理软件不支持对棱边网格方法的支持。同时与相同精度的节点方法相比，未知量的数目要大于节点单元有限元方法[5]。另外，节点有限元方法具有棱边有限元方法所不具有的优点。首先，节点有限元方法的高阶单元非常容易生成；其次对于多物理场问题，由于物理量都是定义在节点上，因此节点有限元方法适合于多物理场的分析。针对节点有限元方法在电磁场问题中的缺点，文[4]采用了罚函数方法消除非物理解，在罚函数方法中，通过加入无散度约束，排除了由矢量场散度不为零所带来的伪解。文[1]对矢量场散度不为零带来的非物理解问题进行了分析，认为非物理解不是理论上的原因，而是数值计算产生的。因此在合适的边界条件下，亥姆霍兹方程的解不会混合有散度和无散度方程的数值解。从而可以避免非物理解产生。文[5]提出了一种基于节点有限元，采用矢势与标势函数计算电磁场的方法。该方法中矢势与标势函数均满足亥姆霍兹类型的方程，根据规范条件要求，提出了两种不同的规范，其中第一种规范标势函数为零，对于介质边界，可以通过加入强制的边界条件满足电场法向分量不连续的要求。第二种规范中，矢势与标势函数都是连续的，它们之间存在耦合关系，这种耦合性质是由于介质的非均匀性质产生。因此该方法可以有效处理电场在介质截面法向分量不连续的问题。

自从有了基于A-φ方法的节点有限元公式以后，对实际三维工程问题的应用还很少在文献中见到。对于工程问题，需要考虑A-φ方法中矢势和标势函数边界条件的实现方法。本文分别对波导端口，散射吸收边界进行了分析，给出了相应的边界条件实现，并且与基于棱边的矢量有限元方法进行了比较，证明了该方法的正确性。对于不均匀介质，分析了矢势和标势通过不连续介质界面的变化情况，以及电场通过不连续介质的变化情况，从而更清楚地了解A-φ方法能够处理不同媒质交界面处场量不连续的特点。

2 标势与矢势有限元公式

根据电磁场理论，电场与磁场可以用矢势和标势函数表示为，

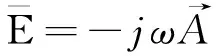
(1)

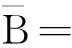
(2)

把1)式代入电场的麦克斯韦公式，得到，

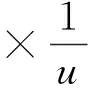
(3)

▽·▽

(4)

为了唯一规定矢势和标势函数，需要加上规范条件，Boyse[5]给出了两种规范条件，第一种规范条件规定矢势和标势的关系为：

▽·2μφ

(5)

第一种规范条件要求矢势函数在不连续界面有一个跳变，与通常对电场和磁场函数的要求是一样的。在第一种规范条件下，矢势方程与标势方程之间没有耦合，同时矢势方程与标势方程都是准亥姆霍兹方程，它们可以给出唯一的，稳定的无散度麦克斯韦方程解。但是仍然存在界面不连续的问题。第二种规范条件由6)式给出：

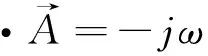
(6)

第二种规范条件允许矢势和标势函数是连续函数，其中包括在不连续界面，因此适合基于节点方法的有限元。但是矢势方程与标势方程之间在非均匀介质情况下存在耦合，同时每个节点需要4个自由度。同样地，它们可以给出唯一的，稳定的无散度麦克斯韦方程解。考虑在第二种规范条件的矢势和标势函数满足的方程为：

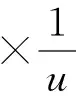
(7)

-▽·▽▽=P

(8)

第一类边界条件，

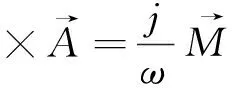
(9a)

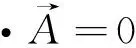
(9b)

φ=0

(9c)

第二类边界条件，

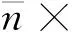
(10a)

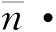
(10b)

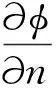
(10c)

利用迦略金方法可以得到弱形式的有限元公式

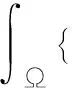
(11)

从以上公式可以看到，当存在不均匀介质时，标势方程和矢势方程存在互偶。

3 应用举例

自从Boyse提出高频A-φ有限元方法以后，1992年给出了关于非均匀介质中有限元计算结果[5]。当时主要是针对二维不均匀介质问题。1997年Boyse给出了针对理想导体问题提出了阻抗边界条件[6]。1998年提出了基于节点的PML有限元方法[7]。然而对于三维电磁场的高频问题的求解还没有在文献中见到。本文的工作是考虑方法的三维应用，特别是针对常见的工程问题的边界条件设置进行了分析研究。在工程应用中，主要是两类问题，一类是开域问题，边界条件主要是应用散射边界条件；第二类是封闭区域问题，波导中电波传播是一种典型的问题，其边界条件主要考虑端口边界条件。下面我们针对这两类问题，研究基于节点的有限元方法边界条件的设置问题，给出相应典型问题的应用。

3.1 矩形波导

矩形波导是很重要的微波器件，利用有限元A-φ方法求解波导传输问题，端口边界条件的设置是非常重要的。利用有限元方法求解研究矩形波导电波传播问题，端口的边界条件由12)式决定，

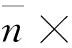
(12)

为了讨论节点有限元处理非均匀介质中场量不连续问题的能力，研究一个波导中有介质片的基本问题。考虑如图1所示矩形波导的电波传播问题，矩形波导中有一个介质片，相对介电常数等于10.对于该波导，由于存在介质片的不均匀性，传统的基于节点方法的有限元公式会出现伪解的问题。但是采用A-φ方法，可以很好地解决这个问题。图2给出了电场Ez分量的场分布计算结果，图2a)是采用棱边方法计算的结果，图2b)是采用节点有限元计算的结果，可以看到两个计算结果是一致的。

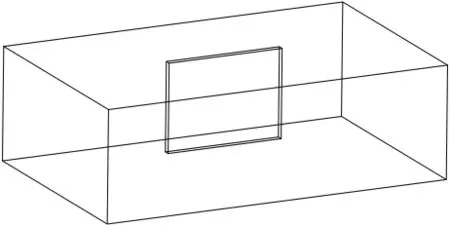
图1 理想导体矩形波导尺寸：a=1.9 cm，b=0.95 cm，l=3 cm；波导中心有一个介质片，长1cm，高0.75 cm，厚0.05cm，相对介电常数10

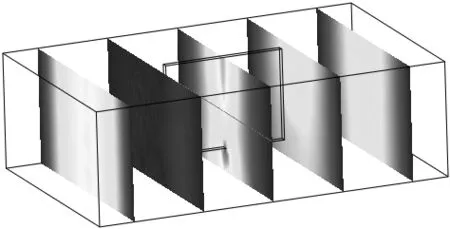
(a)理想导体矩形波导中电场空间分布，工作频率15GHz，采用基于棱边单元的有限元方法

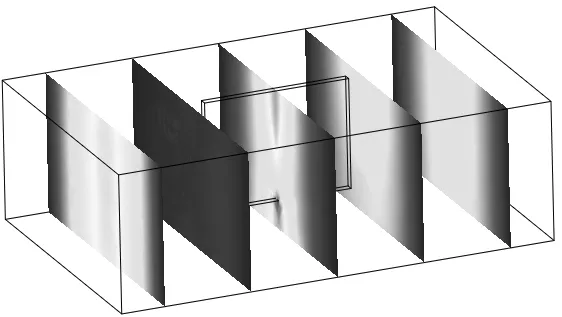
(b)理想导体矩形波导中电场空间分布，工作频率15GHz，采用基于节点单元的A-φ方法图2

为了研究介质不连续对场分布的影响，考虑介质片位置如图3所示。在图3中所画线段是计算中研究场分布的路径，由于路径穿过不连续介质，电场的垂直分量会发生不连续的变化。在传统节点有限元中，由于电场在节点是连续的，因此不能处理这类不连续问题。然而，对于A-φ方法，矢势A和标势φ在节点都是连续函数，不连续性由φ的梯度产生，因此A+▽φ组合在一起，可以处理这类不连续问题。

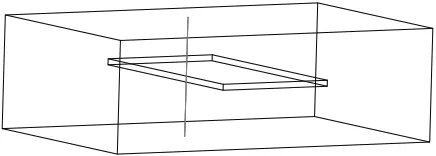
图3 理想导体与介质片参数同图1，介质片平行放置，研究电场穿过介质片的变化分布

从图4的曲线可以看出，通过不均匀介质界面时，矢势是连续函数。由于矢势是连续函数，因此采用基于节点的基函数就不会出现传统采用电场函数所带来的问题。然而，尽管矢势是连续函数，由它和标势函数的梯度叠加形成的电场函数满足原来的电磁场边界条件。

3.2 导体球散射

导体球散射是属于开域问题，散射边界对计算结果影响很大。在A-φ方法中，矢势满足的辐射边界条件为与电场满足的边界条件相同，标势在辐射边界规定为零。导体边界同样用阻抗边界条件进行了处理。对于矢势和标势，相应的辐射边界条件为：

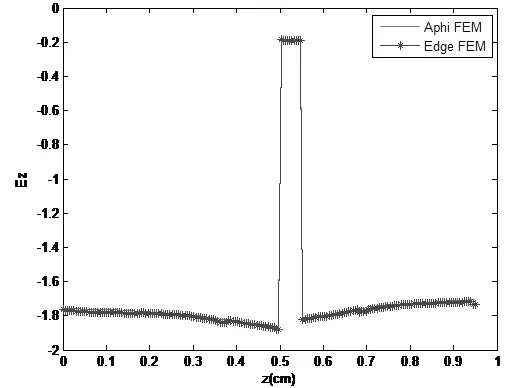
(a)电场z分量通过不连续介质的分布曲线，工作频率15GHz

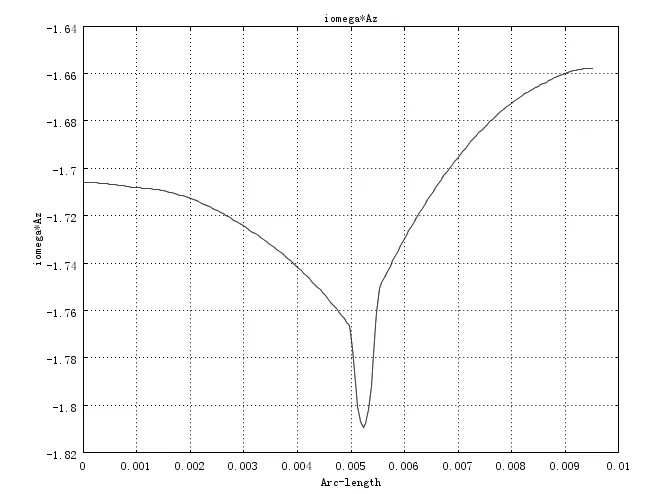
(b)矢势z分量通过不连续介质的分布曲线，工作频率15GHz

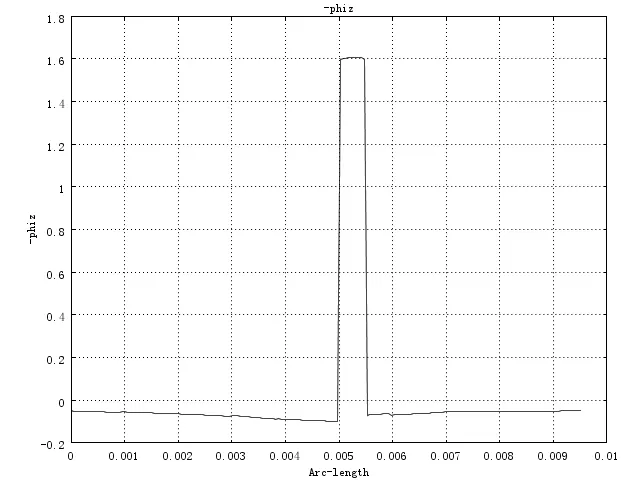
(c)标势梯度z分量通过不连续介质的分布曲线，工作频率15GHz图4

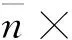
( 13a)

φ=0

(13b)

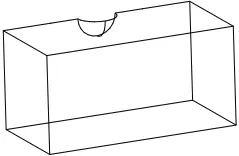
图5 导体球散射问题，考虑散射问题的对称性，计算四分之一结构，球半径0.01米，边界边长0.1米

图6给出了导体球的归一化散射截面随频率变化曲线和解析解的比较，计算结果和解析解吻合很好。

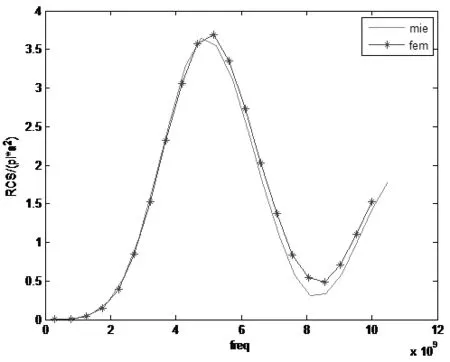
图6 归一化雷达散射界面随频率变化曲线

4 结论

论文基于A-φ节点有限元方法研究了波导中电波传输问题和理想导体球的散射问题。在A-φ方法中，选择合适的洛伦茨规范可以得到适合采用基于节点基函数的有限元公式。该公式可以避免采用电磁场作为求解函数所带来的伪解和不均匀介质出现的不连续问题。计算结果表明通过施加适当的边界条件，基于节点的有限元方法可以得到与棱边单元相同的计算结果。同时，对于非连续介质情况，尽管矢势通过不连续界面是连续的，但是电场的法向不连续性和棱边方法电场的法向不连续结果是一致的。对于散射问题，考虑的对称性，理想导体边界条件，计算区域存在90度两面直角，对于这类导体问题，节点方法在夹角附近存在杂散场解问题，通过采用阻抗边界条件可以有效克服这些问题。理想球体散射A-φ节点有限元方法的数值结果与解析结果进行比较，可以看到两结果符合很好。

参考文献：

[1]D R Lynch，K D Paulsen.Origin of vector parasites in numerical Maxwellsolutions [J].IEEE Trans，Microwave Theory Tech，1991，39(3)：383-394.

[2]Jianmin Jin.The finite element method in electromagnetics [M].John Wiley & Sons Inc，2002.

[3]J C Nedelec.Mixed finite elements in R3 [J].Numer Math，1980，35：315-341.

[4]B M A Rahman，J B Davies.Penalty function improvement ofwaveguide solution by finite elements [J].IEEE Trans，Microwave Theory and Tech，1984，32(8)：922-928.

[5]William E Boyse，R Lynch，Keith D Paulsen，Gerald N Minerbo.Nodal-BasedFinite-Element Modeling ofMaxwell’s Equations [J].IEEE Trans，Antennas Propagat，1992，40(6)：642-651.

[6]William E Boyse，Keith D Paulsen.Accurate Solutions of Maxwell’s Equations Around PEC Corners and Highly Curved Surfaces Using Nodal Finite Elements[J].IEEE Trans，Antennas Propagat，1997，45(12)：1758-1767.

[7]Jingwu Tang，Keith D Paulsen，Shah A Haider.Perfectly Matched Layer Mesh Terminationsfor Nodal-Based Finite-Element Methods in Electromagnetic Scattering [J].IEEE Trans，Antennas Propagat，1998，45(12)：507-516.