论Bessel波束超光速现象

黄志洵

(中国传媒大学信息工程学院，北京 100024)

1 引言

自1987年J.Durnin等[1]提出Bessel波束这种独特的波动形式以来，研究者日渐增多。由于它已用在从声波到光波的宽广频域，其意义已不限于电磁波。Bessel波束在一定情况下会呈现出超光速性(superluminality)，这就引起了人们更大的兴趣。本文是对研究状况的简要评述。值得注意的是，中国科学家发表了相关领域的多篇论文[2～4]，非常可喜，证明了国内专家学者在关注科学问题方面的广泛性。

Bessel波束技术是由理论预言到实验成功的范例之一，它丰富了波科学和超光速物理的内容。而它的基础在于数学物理方法中的圆柱函数理论。

2 波科学研究中的圆柱函数[5，6]

18世纪时开始了“科学的数学化”进程。1750年以后L.Euler开始用级数方法求解某些微分方程。1759年他研究了矩形鼓膜和圆形鼓膜的振动，分别得到以下的偏微分方程：

其中(x，y)和(r，φ)是矩形膜和圆形膜上任一点的坐标，z是垂直位移，c是由膜决定的常数。Euler取下述函数试解圆形膜方程：

z=u(r)Sin(ωt+α)Sin(mφ+β)

故u(r)满足

(1)

式中k0=ω/c；这在后来被称为Bessel方程，其标准形式为：

(2)

式中m是方程的阶；可见Euler导出的方程与Bessel方程标准形式只有微小的区别。1818年F.W.Bessel找到方程的一个特解Jm(x)，称为m阶第一类Bessel函数。它是一个无穷级数，当x较小时可写成正幂级数形式：

(3)

式中n！=1·2·3·4……n；Jm(x)有无限多个零点，其值的变化有周期性；例如取m=0，1；即得

(4)

(5)

图1是m=0，1，2，3时的Jm(x)函数曲线，注意只有J0(x)是在x=0时函数值不为零。

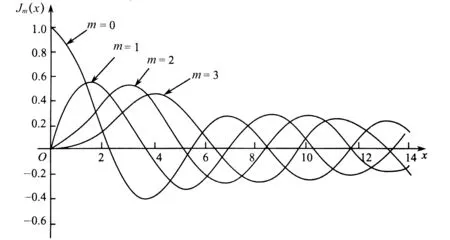
图1 Bessel函数图像

当x较大(例如x≥13时)，可用渐近公式计算Jm(x)：

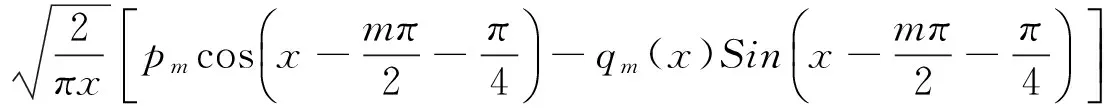
(6)

式中

(7)

(8)

由于方程(2)的通解为

y=aJm(x)+bNm(x)

(9)

因此还应了解m阶第二类Bessel函数N(x)，它简称Neumann函数。当m为整数时有

(10)

这时有一个称为Weber解的级数展开式：

(11)

故把m的值(例如：0、1……)代入即可计算函数值。Nm(x)也是振荡型的实函数；但当x=0时Jm(x)为有限值或零，而Nm(x)为无限大。在电磁理论问题中，必须考虑到不同柱函数的不同特点。

和Jm(x)一样，在x较大时可用渐近公式：

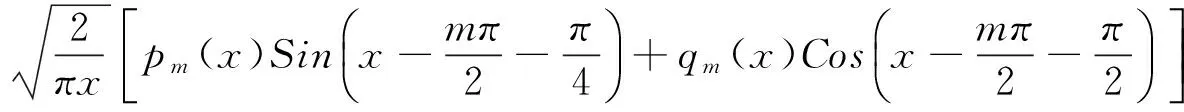
(12)

以上就是1867年C.G.Neumann发展Bessel函数的基本内容。

1869年H.Hankel讨论了Jm(x)与Nm(x)的线性组合，结果产生了Hankel函数：

(13)

(14)

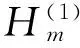
当x较大时，也有所谓渐近公式成立：

(15)

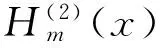
(16)

现在来看修正Bessel方程(modified Bessel equation)，这是以jx代替x之后由(2)式得出的：

(17)

它也叫虚宗量Bessel方程(Bessel equation of imaginary argument)，通解为

y=aIm(x)+bKm(x)

(18)

Im(x)是m阶第一类修正Bessel函数，Km(x)是m阶第二类修正Bessel函数。后者也叫Beset函数；当x为实数，Km(x)是实函数。现在Im(x)、Km(x)均非振荡型，不存在实的零点。Km(x)的特点是，当x增大时函数值逐渐减小。从应用上看，Km(x)是很重要的；例如1893年J.J.Thomson对金属壁圆波导的分析(波导出现于1936年，但Thomson很早就做过数学分析)，是假设一个电介质圆柱体嵌埋在无限大的导电媒质之中(该电介质实际上可能是空气)；这时他假定在介质内场按Bessel函数变化，在导电媒质内场按第二类修正Bessel函数(即Km)变化；笔者在专著《截止波导理论导论》[7]曾详细介绍了Thomson的很有特色的数学分析过程。

Beset函数的定义为：

(19)

其幂级数展开式与Nm(x)有些相似：

(20)

而在|x|较大时Km(x)的渐近展开式为

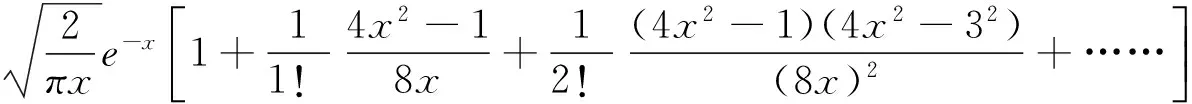
(21)

若|x|>5～6，可简化为

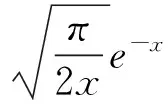
(22)

对于圆介质波导和光纤，上述式子均可用来描写场分布(只要把x改为径向坐标r)，即无限远处场为零。又如分析金属壁圆波导的早期工作(J.J.Thomson)，也成功地运用了(22)式的表达方式。……另外，Km与Bessel函数有以下关系：

(23)

由此可证：

(24)

总之，函数Km(x)随x增大而逐渐减小的特性，在电磁理论与波科学中具有独特的应用价值。实际上它与函数e-αx有类似之处，因此消失态(evanescent states)的某些特征也能在这里找到。这也是本文后面所述的“Bessel波束超光速现象”的一种数学物理解释。

3 Bessel波束的特性

光在传播过程中因波前受物体影响而偏离直线的现象称为光的衍射，具体分为近场衍射和远场衍射。1987年美国Rochester大学的物理学家J.Durnin等[1]发表题为“无衍射波束”(diffraction-free beams)的论文，从理论上预言了一种新的波动形式。众所周知电磁理论中的标量Helmholtz方程为

(25)

其中h2=2+k2=2+ω2εμ，=α+jβ；而波函数ψ=ψ(x，y)或ψ(r，φ)；h称为本征值或特征值。Durnin指出，正是这个方程存在无衍射模波解(a class of diffraction-free mode solutions)；首先，各个平面波都是这种解，但并不限于此。Durnin提出以下波解[1]：

ψ(x，y，z)=J0(αρ)ejβz

(26)

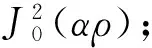
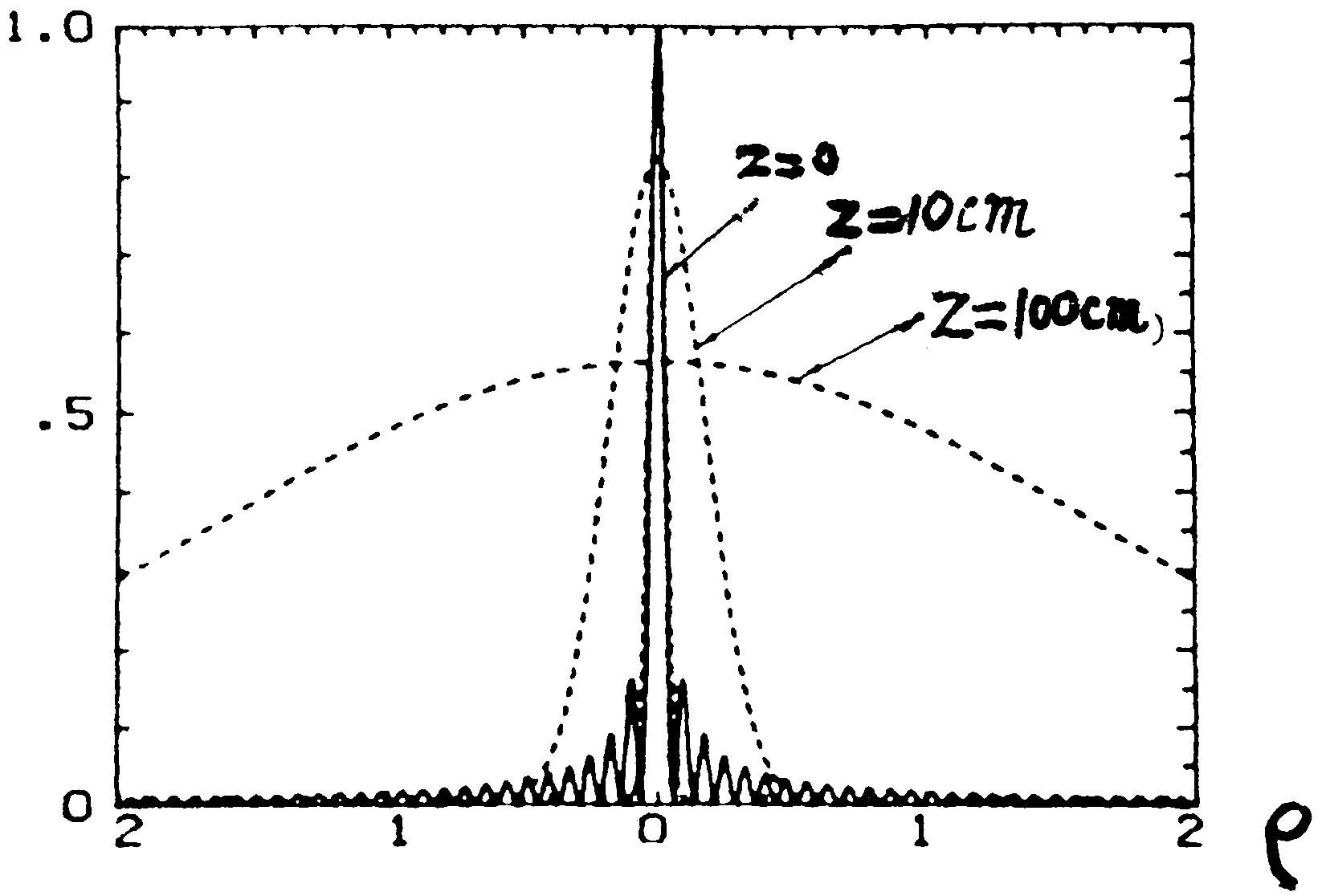
图2 Bessel波束与Gauss波束比较

这就是对Bessel波的研究的开始。Durnin等还做了实验，J0波束其形成是用一个CW激光器，配合使用一个环状缝隙和一个准直化透镜，见图3。图中d=2.5mm，△d=10μm，R=3.5mm，f=305mm。总之，早期研究强调这种波束在大距离上保持其尖锐的成峰径向外廓的特性。

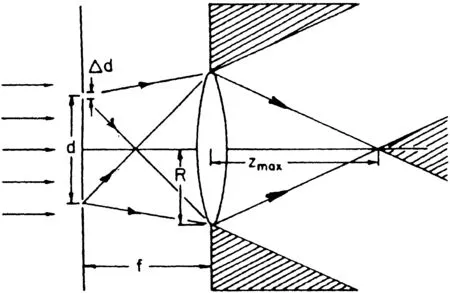
图3 在光频实现Bessel波束的方法

在1987年-1997年期间，Bessel波束在光学、声学方面有所应用；后来又被称为X波(X waves)或Bessel-X脉冲(Bessel-X pulse)。1997年P.Saari等[8]在光频对X波进行实验测量，获得了场的整个3D分布，并把实验结果图形与计算机模拟进行比较。在论文中Bessel波束可表为

EB(ρ，z，t，k)∝J0(ρSinθ)ejk0z cosθe-jωt

(27)

式中z是传播方向，ρ是从z轴起算的横向距离，θ是圆锥角。对于X型场，考虑不同频率时的频谱表达式为

(28)

这就是Bessel-X型脉冲；上式可用电脑计算(ρ，z)平面上的场分布，呈X形状，即X shaped profile。

总之，早期关注Bessel波束振幅与z无关，传播中形状不变，这是不平常的特性。2005年D.Mugnai等[9]讨论了Bessel波束的能量局域化和能速(energy localization and velocity of a Bessel beam)问题。他指出，研究的困难首先在于找出能描述整个系统的矢量场，因为过去对Bessel波束都是用标量场作近似表达。选取球坐标系(ρ，θ，φ)，则Bessel波束是包含一组平面波的组合，它们以同一角度θ0(θ0<π/2)按照下述方向传播：

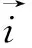
a=Sinθ0cosφ，b=Sinθ0Sinφ，c=cosθ0

(29)

对于在真空或空气中的传播，在点(x，y，z)的每个波可写作：

E(x，y，z)=E0dφ·ejk0(ax+by+cz)e-jωt

(30)

其中E0是子波振幅；然而对圆柱坐标系(ρ，ψ，z)而言有：

x=ρcosψ，y=ρSinψ，z=z

因而积分后可得总场

(31)

上式是标量场；那么如何在矢量场基础上进行分析？Mugnai等进行了探索。所用方法是另行设计一个理论上进行模拟的体系，它可产生一种类似矢量场表示的情形，进而可计算场强、能流和能速。但这套方法不是直接的对Maxwell方程组求解分析。

4 Bessel波束超光速现象

(32)

而cosθ0<1；这是与z轴垂直的波前速度(vp>c)。在无色散时Bessel脉冲的群速也是这个速度，即

(33)

这些是Bessel波束速度讨论的基本出发点。Mugnai[10]论证说，信号速度(vs)也是这个值，故vs>c，信号传播超光速。这个观点引起很大争议。一种看法是，Mugnai报告的超光速现象是由于在对称轴上球面波前干涉所致，实际上仅仅脉冲峰作超光速传送(only the peaks of pulses travel at superluminal speed)。T.Sauter[11]的意见如下：“无可争辩，Bessel波束表面上造成局域化波包以超光速沿对称轴运动。但这个运动不能与一个粒子或一个惯常的波相比拟。实际上，波包是多个以光速传播的波互相干涉所致。这些特别的波可否用于超光速信号传递？这行不通。即使信息接收器安装在轴上，发送器却不是，实际上离开了轴，故不能沿轴发送信号。故Bessel波束不适用于超光速信号传送”。他的意见可供参考。

对于“Bessel-X波超光速性”(superluminality of Bessel-X waves)，我们了解到的主要实验是2000年D.Mugnai[12]在微波进行的实验，目的是观测Bessel波束的超光速现象。实验波长λ≅3.5cm，实验装置见图4，显然是对Durnin[1]的模仿；圆形缝隙平均直径7cm(或10cm)，而球状mirror的直径2R=50cm，聚焦长度f=12cm。圆锥角取为16°或23°，对波速带来增量4%或8%。这些情况与光频实验颇为不同，例如后者θ<1°。

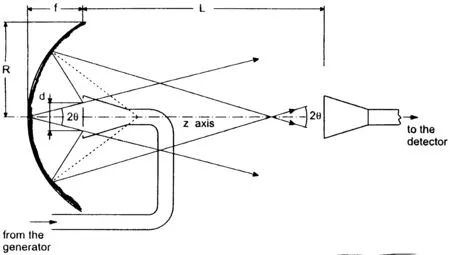
图4 微波Bessel波束超光速实验

Mugnai等以实验演示了超光速波传播，这类波优于消失模隧穿，因后者常常只在几厘米距离上表现出来(消失模特性决定了距离很短)，现在的演示可达1m以上。图5是测量微波传播速度的发送与接收天线系统，D是圆形辐射缝隙的平均直径，实验时取D=7cm以及10cm。信号形式为微波脉冲，载频f=8.6GHz(波长λ约3.5cm)，调制为矩形脉冲(升降时间均在纳秒级)。用Tektronix公司的双路数字示波器TDS680B检测时延，实验方法为，改变发送天线与接收天线的间距(L=0.3m～1.3m)，作时延测量。图5中包含时延τ与距离L的关系，实际测量值用黑色圆点表示，它们联成一条直线，其斜率比光速线略小，由此可知实际的波速比光速略大：

(34)

即比光速c大了5.3%；这个v值是平均的电磁波速度。

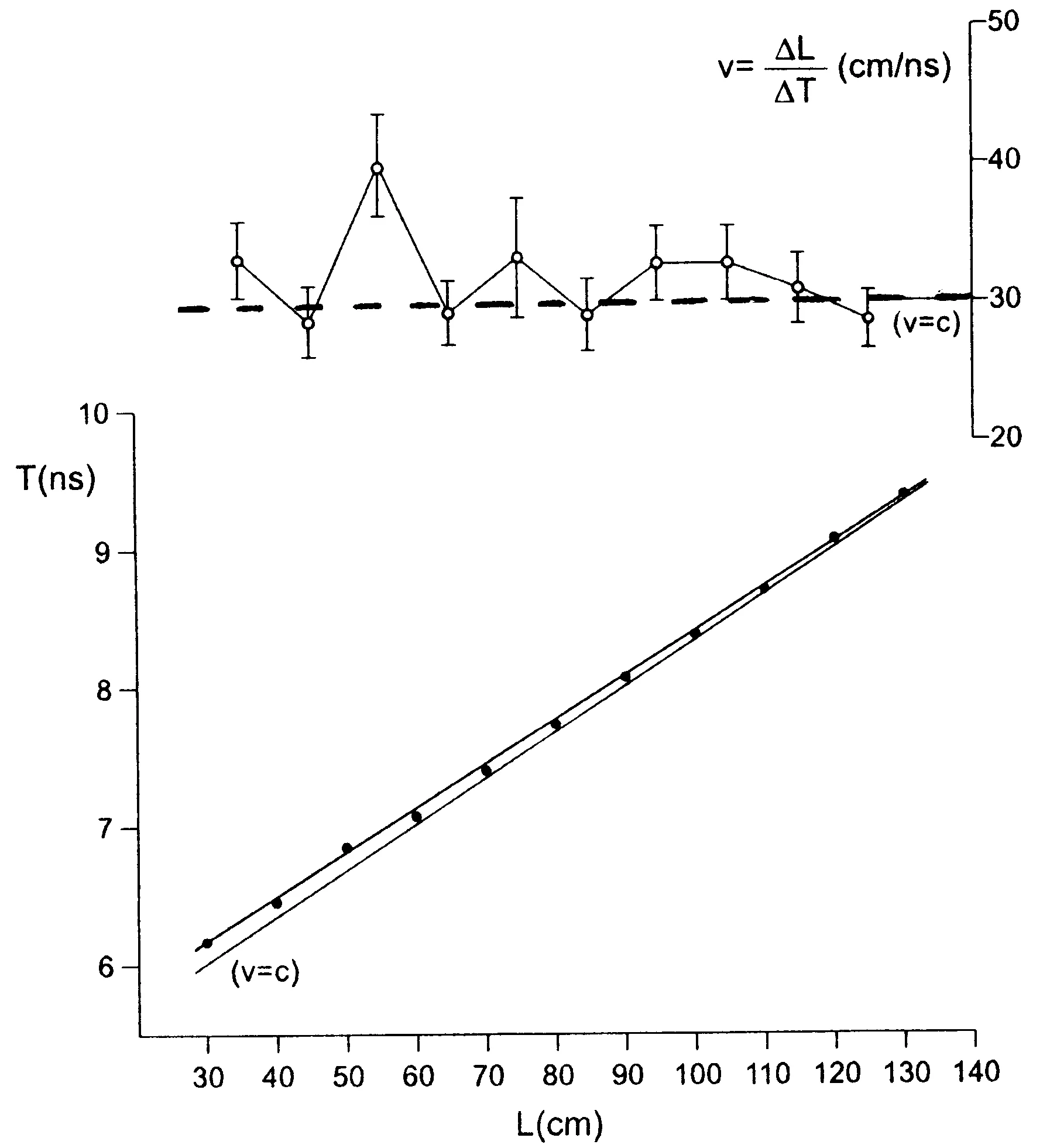
图5 辐射缝隙直径7cm时的实验结果

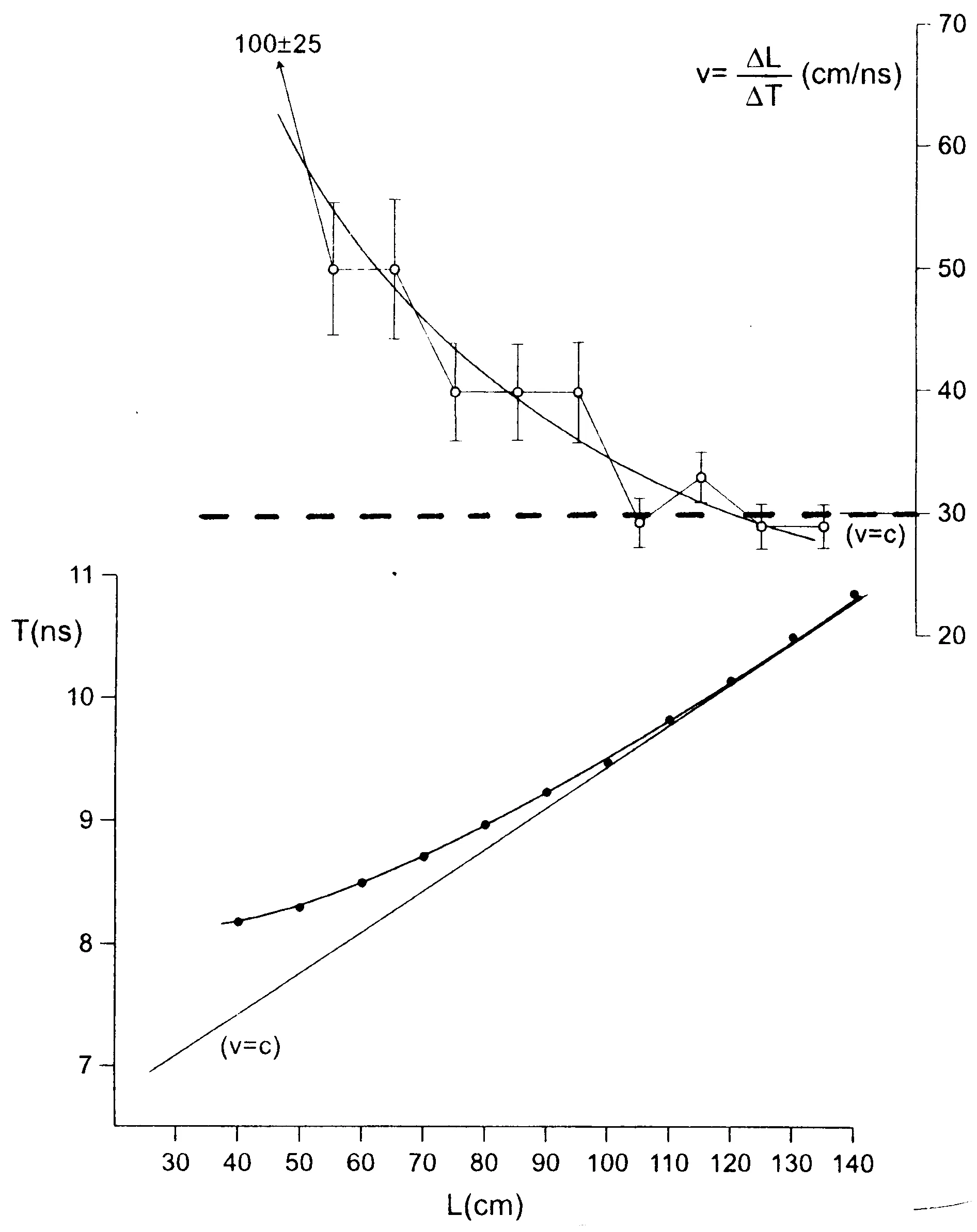
图6 辐射缝隙直径10cm时的实验结果

图5和图6是在选取不同的Slit直径时测得的结果。很明显，在直径10cm时，超光速现象更为突出：只要L<1m，结果就都是超光速的。

2006年王智勇、熊彩东[4]的论文虽非实验研究，但其理论分析和数值计算结果令人耳目一新。他们首先说“Bessel波即使不经过一个隧穿区，也有超光速现象”。然后指出：不仅实宗量普通Bessel波如此，修正Bessel波，由虚宗量Bessel函数描写，也有群速超光速vg>c的情况发生，并有以下特点：①当传播距离加大时群速会增加，这与平面消失波情况类似；②波数加大时群速减小，这也与平面消失波情况类似；③在波数小时，波数加大时群速加大，这与平面消失波情况不同。……必须指出，在虚宗量Bessel波的讨论中，当然要用Beset函数Km(x)，见本文第2节。

当所描述的波束由r1传播到r2，计算得到的比值vg/c与 (r2-r1)呈线性正比关系，见图7；这与Hartman效应[13]的描述是一致的。另一方面，图8是计算得到的比值vg/c与k的关系，可以看到在波数小(k<1.2)时的规律与波数大时(k>1.2)时的规律是不同的。在图7中，虚线表示平面消失波的情况。(注：图8的计算是在一定的距离之下得到的——取(r2-r1)=10)。我们注意到，计算表明vg/c之值是较大的。

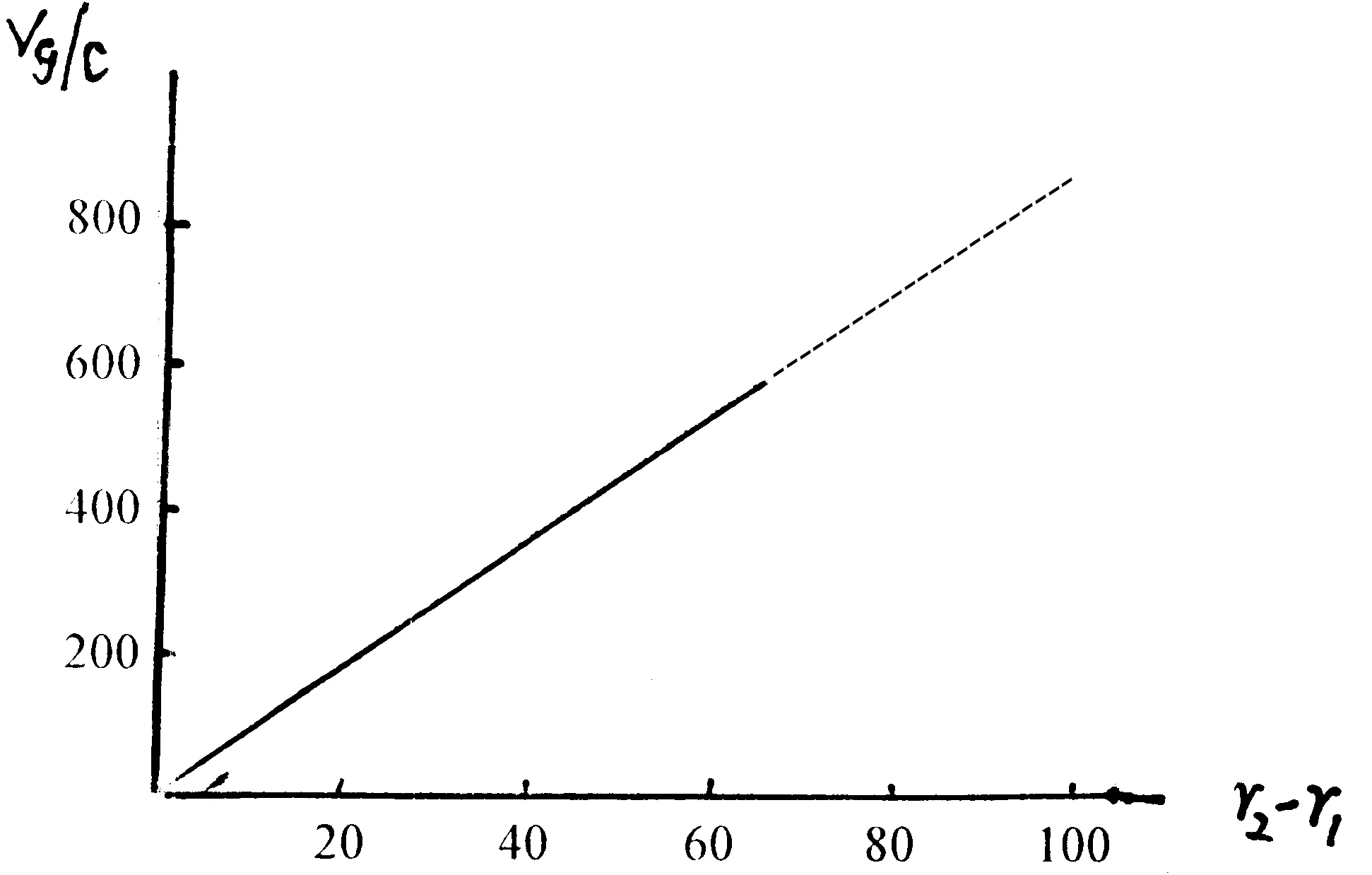
图7 群速与传播距离的关系

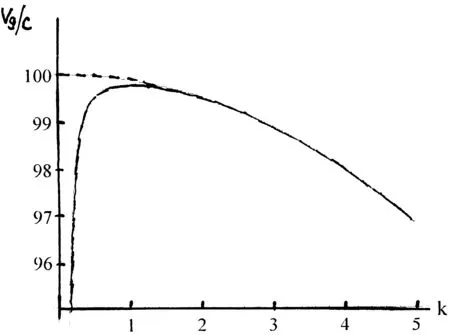
图8 群速与波数的关系

在不久前的讨论中，王智勇向笔者说明了他的工作和观点：假设有两个半径一样大的金属圆板，平行放置，二者间距为D，且二者圆心的连线与这两个圆板垂直，即这两个金属圆板一起构成一个高为D的圆柱的上下底面，但这个圆柱没有侧面，这两个圆板的圆心在圆柱的轴线上。假设在这两个金属原板之间，在圆柱的轴线处，有一个电磁波的波源，产生的电磁波沿圆柱径向向外传播，波前是圆柱面(圆柱波)，这个圆柱波就是Bessel波(圆柱波是行波时，由实宗量的Bessel函数描述。)如果这两个圆板之间的距离D足够小(或者D固定而圆柱波的波长足够长)，会导致这个圆柱波不再是行波，而是沿径向呈指数衰减的波，此时的圆柱波就变成虚宗量的Bessel函数所描述的波，与光子的量子隧穿相对应。他的描述是生动的和有启发性的。

5 结束语

近年来在科学文献中常常出现“Bessel波”和“X波”这两个词，这是通常的论述电磁场和电磁波的理论书籍中没有的，比较令人费解。初步的文献追踪表明，这一领域在众多科学家努力下已取得显著成绩，但也留存若干待解决的问题。例如，现在只有Bessel—X波的标量场表达，更深刻的矢量场理论似未建立；对超光速现象的物理本质也就不甚清晰。又如，对于王智勇、熊彩东论文[4]，是否可以再前进一步，看看有没有获得负群速的可能？因为国内外的许多论文，从超光速群速到负群速只是一步之差。这些问题尚待研究。

作者感谢与王智勇副教授的有益讨论。

[1]Durnin J，et al.Diffraction-free beams[J].Phys Rev Lett，1987，58(15)：1499-1501；又见；Durnin J，Exact solutions for nondiffracting beams：the scalar theory[J].J Opt Soc Am，1987，4(4)：651-654.

[2]Lu X H(陆璇辉)，et al.High order Bessel-Gaussian beam and its propagation properties[J].Chin Phys Lett，2003，20(12)：2155-2157.

[3]Zhang Y(张颖)，Gao B Q(高本庆).Propagation of cylindrical waves in media of time- dependent permittivity[J].Chin Phys Lett，2005，22(2)：446-449.

[4]Wang Z Y(王智勇)，Xiong C D (熊彩东).Superluminal behaviors of modified Bessel waves[J].Chin Phys Lett，23(9)：2422-2425.

[5]Kline M.Mathematical thought form ancient to modern times[M].New York：Oxford Univ Press，1972.

[6]梁昆淼.数学物理方法[M].北京：人民教育出版社，1979.

[7]黄志洵.截止波导理论导论[M].第二版.北京：中国计量出版社，1991.

[8]Saari P，Reivelt K.Evidence of X-shaped propagation invariant localized light waves[J].Phys Rev Lett，1997，79(21)：4135-4138.

[9]Mugnai D，Mochi I.Bessel beam propagation：energy localization and velocity[J].arXiv：Physics./0506120V2，[Physics.optics]，16 Jun 2005.

[10]Mugnai D.Bessel beams and signal propagation[J].Phys Lett A，2000，278(Dec.18)：6-8.

[11]Sauter T，Paschke F.Can Bessel beams carry superluminal signals[J].Phys Lett A，2001，285(Jun.25)：1-6.

[12]Mugnai D.Observation of superluminal behaviors in wave propagation[J].Phys Rev Lett，2000，84(21)：4830-4833.

[13]Hartman T E.Tunneling of a wave packet[J].J Appl Phys.1962，33：3427-3433.