基于隐马尔科夫模板模型的视频动作识别算法

李 庆，师小凯

(武汉理工大学光纤传感技术与信息处理教育部重点实验室，湖北 武汉 430070)

如何从视频中识别人类的动作和行为是当今计算机视觉和模式识别领域内的热点问题。该项研究在智能安防、视频检索、人机交互与自主机器人等现代计算机应用领域有着广阔而深远的影响。当前业界对该问题的主要解决方法包括两种:①双目摄像机深度分析;②单目摄像机视频分析。其中，双目摄像机深度分析在家庭人机交互方面也得到了长足的应用，然而这类方法需要特殊的数据采集设备，因此在视频监控和视频检索领域的应用受到限制。单目摄像机视频中的行为识别技术应用的范围更广，但其实际应用仍然是一个非常有挑战的问题。目前基于单目摄像机视频中的行为识别主要有3种方法:

(1)基于模板匹配的方法。该方法认为，行为可以由一组模板集来描述，ESSA和 PENTLAND［1］用光流特征建立了一套完备的脸部模板集，通过模板匹配的方法实现识别。BOBICK和DAVIS［2］用运动历史图来获取运动和形状特征，然后用获取到的运动和形状特征来表达行为，用全局描述符(运动能量图和运动历史图)作为模板，通过与标准的模板集进行配对实现动作识别。这种方法有两个局限性:①依赖稳定的前景分割，即运动的目标可以从静态背景中分割出来，而笔者所提出的算法没有这个限制;②这类方法中运用的是刚性模板，对于视角和运动目标的外观变化很敏感，而笔者采用的活动模板就没有这方面的局限。

(2)基于时空兴趣点的方法。该方法能够克服视频序列中目标在几何外观上变化。LAPTEV等［3］提取时空兴趣点，并且在这些点的附近提取HOG和HOF特征，用提取到的特征来训练用于动作识别的SVM判别器。在动作识别方法的实现步骤中，需要建立词袋模型(bag of words，BoWs)［4－5］。在词袋模型的建立过程中，运用 K-means算法实现聚类，当有大量数据需要聚类时，会存在计算时间和空间复杂度的问题。时空兴趣点属于局部特征，在动作识别的过程中需要构建这些局部特征间的关系。

(3)基于时间状态－空间模型的方法。该方法包括两个方面:状态集和相连边［6］。状态集包括观测值和状态值，观测值表示某种行为的视频中的每张图像，那么状态值即为该时刻动作的表示，经常作为该动作内部分类的标志;相连边表示各个状态的状态间转移概率和观测值与状态间的观测概率。

笔者采用的算法基于第3种方法，观测值是相邻的两张图像，观测值与状态值之间的关系由一套活动模板决定，这套活动模板包括形状和运动模板，通过模板匹配的方法可以构建观测值与状态间的观测概率，通过隐马尔科夫模型来描述局部特征关系。相比第1种方法，模板的学习不需要依赖于前景分割，学习出来的活动模板在模板匹配时允许在方向和位置上有一定程度的变化，因此对于视角和外观的变化有较好的鲁棒性;相比第2种方法，运用马尔科夫模型描述了动作局部特征的关系，不需要大量的手工标注，通过弱监督的机器学习就可以达到目的。

1 隐马尔科夫模板模型

1．1 模型建立

隐马尔科夫模板模型(HMT)如图1所示。圆圈里面的内容为状态变量，方框中的内容为函数关系。It为t时刻的输入图像，Ft为(t+1)时刻和t时刻的图像计算出来的光流图，而t时刻的观测值ot由t时刻的输入图像和t时刻的光流图组成，即ot={It，Ft}。每个时刻的观测值都对应有一个状态值 qt，状态值 qt是隐性的(即未知的)，并且是离散的，qt∈S，S为行为的状态集。

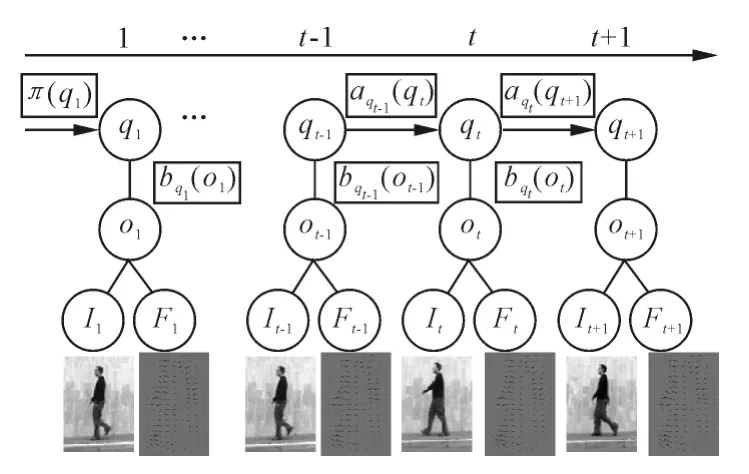
图1 隐马尔科夫模板模型示意图

由上所述，在参数已知的情况下，观测值和状态值的联合概率可以由式(1)表示:

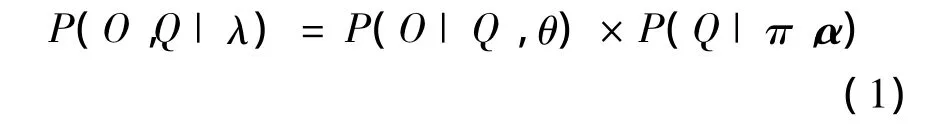
由于t时刻观测值ot的概率仅与所处状态有关，与其他变量无关，因此式(1)右边P(O|Q，θ)可以表达为:

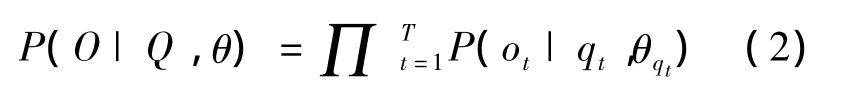
可以将式(1)分解为:

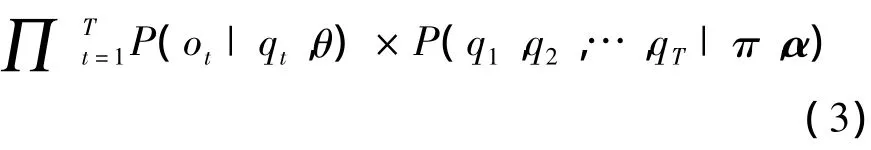
又因为HMT的假设2，在t时刻的状态仅与t－1时刻的状态有关，因此式(1)可以分解为:

1．2 模型的概率表达形式

给定一组特征集B，某一时刻的观测值O(为表达方便省去时间下标)可表示为:

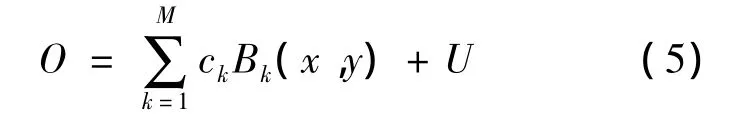
式中:Bk为图像的第k个“基”;M为图像的形状和运动特征，可用M个Base来表达;坐标(x，y)为每个“基”所在的位置;ck为第k个“基”的系数;U为图像的背景部分;B1，B2，…，BM为从集合B中选出被用于表示观测值O的特征集，集合B中包括盖博小波基和光流块;c=(c1，c2，…，cM)为系数的集合。笔者采用类似文献［7－8］中的方法去选择“基”。

根据文献［7］的结论，在状态已知的情况下，图像O的似然函数可由式(6)表示:

式中:q(O)为归一化常数;ri={ri1，ri2};ri1为观测值与第 i个“基”内积的响应，ri1(x，y)=〈o(x，y)，Bi〉，其中(x，y)为第 i个“基”与图像(x，y)位置的区域进行内积;ri2为背景图像I与第i个“基”内积的响应，ri2(x，y)=〈I(x，y)，Bi〉，其中(x，y)为“基”与背景图像 I的(x，y)位置的区域进行内积。类似地，可以假设ri={ri1，ri2}在目标前景上和图像背景上都服从高斯分布，如式(7)所示。

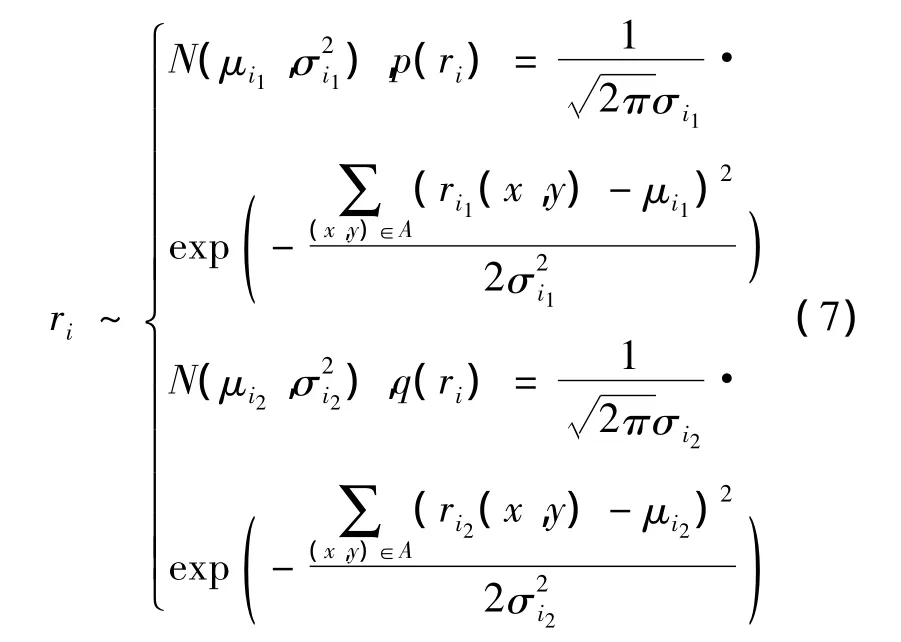
式(7)中的高斯参数(μ，σ)可以通过对像素点的统计得到。

1．3 模型推理

1．3．1 给定类别对数据O的最优理解

在这里参数λ已知，数据O已知，每个数据对应的隐含变量Q未知，可以采用MAP方法求解数据分类:

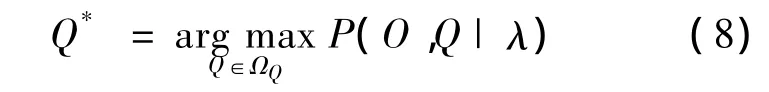
由于P(O，Q|λ)是以视频段为单位计算的，各个视频段之间相互独立，而每个视频段的计算方法是一样的，以求一段视频的隐含变量为例，为了简化求解重新定义 O={o1，o2，…，oT}，对应的隐含变量为 Q={q1，q2，…，qT}，这段视频表述的行为被分为M种姿态。那么每个时刻的隐含变量qt都有M种可能，总共有T个时刻，如果要用穷举法的话，就会有MT种情况，则相应找最优解的计算复杂度为O(MT)。在视频长度T很长的情况下，幂数级的计算复杂度是不能容忍的。为了降低计算的复杂度，笔者采用动态规划方法来使计算的复杂度降为多项式级。

1．3．2 未知类别求最优分类

定义动作类别 A∈ΩA={1，2，…，10}，即识别动作的种类数为10。在动作A的HMT参数λA通过学习后得到参数集 λ ={λ1，λ2，…，λi，…}，给定一段视频，它所表述动作的类型可以通过式(9)计算:

确定该段视频所代表的动作类型，中间式子表明是通过求该动作类型最大后验(MAP)得到的，右边式子的物理意义是:用所述方法求出行为集中每种行为对应的最大联合概率，需要解释的是ΩQA为动作A的姿态集，再通过比较每个行为的最大联合概率，找出其中的最大值，其对应的动作A，就是最终识别结果。

1．4 模型参数估计

EM算法就是在已知数据的情况下寻找参数的最大后验概率的一种算法，由于参数未知，因此，首先要通过对参数初始化，然后估计参数的期望值，使数据的最大似然概率最大，从而估计出新的参数，如此反复直到最后收敛为止。

由于不知道 P(O|λ)，只知道 P(O，Q|λ)，其中Q为隐含变量，因此必须使用迭代方法，首先初始化λ0，然后得到状态Q1，在每一轮循环中迭代估计出新的λ和Q，直到收敛为止。这是借用了EM算法的思想，即:

λ0→Q1→λ1→Q2→…→λ*

2 实验结果

笔者所使用的实验数据为Weizmann dataset，1/2用于动作模板的学习，1/2用于识别。实验数据中包含 10 种行为:bend，jack，jump，pjump，run，side，walk，wave1，wave2 和 skip。针对这 10 种行为，运用所提出的算法将它们各个动作的模板都学习出来，采用40个Gabor基和40个光流基组成活动模板，这些基(Gabor基和光流基)的选择方法具体参见文献［7］。通过HMT模型学习之后得到一套动作模板和一组HMT模型参数。每个姿势对应一个模板，每个模板包括形状模板和运动模板。HMT模型参数包括状态间的转移矩阵和初始化向量。训练这些模板，总共使用了195张图像，每张图像的大小为120×90像素，Gabor的长度为18个像素，分类的总数为4，迭代次数为4。

算法分成两组，一组学习，一组识别。学习算法是在HMT模型的基础上，依据上述模型推理原则，以循环迭代求解最优模型参数的方法实现，图2显示了循环迭代的中间试验结果。从结果中可以看出由于初始化的随机性，在1次和2次迭代中受到背景干扰，出现“毛刺”，姿态模板间的区分度不大。但是随着迭代次数的增加，姿态模板克服了背景干扰，并且姿态模板间的区分度也变得越来越大。

图2 循环迭代学习算法中间结果

识别算法基于模板匹配算法实现，输入图像和模板的相似度可由式(7)得到。为了得到最佳的识别结果，笔者根据状态间的转移规律提出两种模型:左向右型HMT和遍历型HMT。左向右型模型即当前状态能转向自己或者转向相邻的下个状态，状态间的切换有限制;遍历型模型即状态间可以任意转换，状态间的切换没有限制。图3显示了基于特征和姿态数目的识别结果。结果表明提取运动和形状联合特征时，左向右型HMT在识别准确率上有明显优势，考虑到效率问题，每个动作被分为4个姿态就足够了，如图4所示。

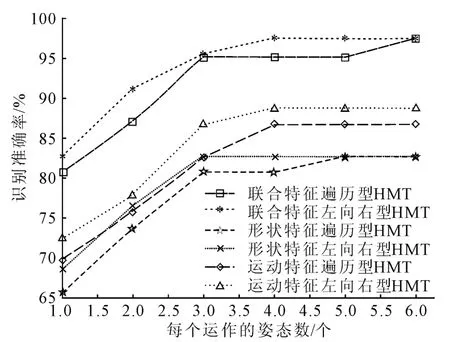
图3 基于特征和姿态数目的识别结果

图4 动作跑的部分识别结果

HMT模型的跑步学习到初始状态向量为π=［0．0，0．4，0．3，0．3］。状态转移矩阵如图5 所示。

图5 动作跑的状态转移矩阵

图6混淆矩阵展示了实验的识别统计结果。横坐标表示实际的动作类型，纵坐标表示识别的类型，图6中交点的坐标值表示识别率，如果横向和纵向对应值相同，就是正确的识别率，如果横向和纵向对应值不同，则是错误的识别率。每一行的数值相加等于1。

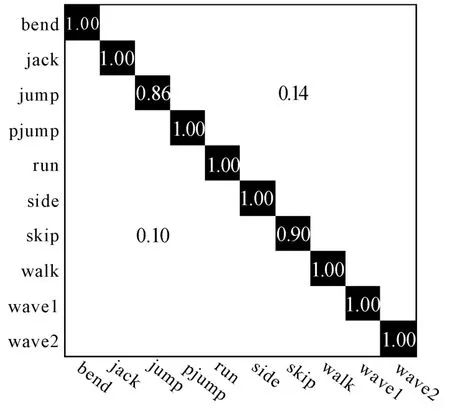
图6 混淆矩阵

所提出的方法充分考虑到姿态间的转换关系，用活动模板表示每种姿态，以克服目标的几何变化;对于“基”与前景和背景图像的响应既符合高斯分布的假设，也符合实际情况，因此在同类方法中，准确率有明显的优势。不同方法的行为识别准确率对比如表1所示。

表1 不同方法的行为识别准确率对比

3 结论

笔者提出了一种基于HMT模型的行为识别方法，HMT模型能够充分地利用行为姿态间的转换规律进一步增强识别效果。基于EM算法来估计HMT模型的参数，解决了先验知识少的问题。

［1］ ESSA I，PENTLAND A．Coding，analysis，interpretation，and recognition of facial expressions［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19(7):757 －763．

［2］ BOBICK A，DAVIS J．The recognition of human movement using temporal templates［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23(3):257－267．

［3］ LAPTEV I，MARSZALEK M，SCHMID C，et al．Learning realistic human actions from moves［C］∥CVPR．［S．l．］:［s．n．］，2008:1 －8．

［4］ SCHULDT C，LAPTEV I，CAPUTO B．Recognizing human actions:a local SVM approach［C］∥ICPR．［S．l．］:［s．n．］，2004:32 －36．

［5］ DOLLAR P，RABAUD V，COTTRELL G，et al．Behavior recognition via sparse spatio－temporal features［C］∥ICCV Workshop on Visual Surveillance and Performance Evaluation of Tracking and Surveillance(VS － PETS)．［S．l．］:［s．n．］，2005:65 －72．

［6］ 江焯林．基于计算机视觉的人体动作检测和识别方法研究［D］．广州:华南理工大学图书馆，2010．

［7］ WU Y N，SI Z Z，GONG H F，et al．Learning active basis model for object detection and recognition［J］．Internal Journal of Computer Vision，2010，90(2):198 －235．

［8］ BENJAMIN Y，ZHU S C．Learning deformable action templates from cluttered videos［C］∥Computer Vision，2009 IEEE 12th International Conference on Digital Object Identifier．［S．l．］:［s．n．］，2009:1507 －1514．

［9］ CAO L，TIAN Y，LIU Z，et al．Action detection using multiple spatial－temporal interest point features［C］∥ICME．［S．l．］:［s．n．］，2010:340 －345．

［10］ KLASER A，MARSZALEK M，SCHMID C，et al．Human focused action localization in video［C］∥ECCV．［S．l．］:［s．n．］，2010:219 －233．

［11］ NIEBLES J，CHEN C，FEI－FEI L．Modeling temporal structure of decomposable motion segments for activity classification［C］∥Computer Vision ECCV 2010．［S．l．］:［s．n．］，2010:392 －405．

［12］ HOAI M，LAN Z，LA TORRE F D．Joint segmentation and classification of human actions in video［C］∥CVPR．［S．l．］:［s．n．］，2011:3265 －3272．