基于自组织数据挖掘的上市公司财务危机预测

张秋菊，朱帮助，刘致秀，马淑姣

(五邑大学经济管理学院，广东 江门 529020)

国外学者很早就开展了上市公司财务危机相关研究。PZARTIKC首次借助对危机公司与非危机公司财务指标的比较分析，发现对于财务危机判别能力最高的是净利润/股东权益和股东权益/负债两个比率。此后绝大部分研究沿袭该思想，运用财务指标对公司财务危机进行预测。1980年开始，随着决策有用性会计目标的流行，现金流量信息受到了普遍关注，一些学者尝试运用现金流量信息预测企业财务危机，如AZIZ等比较分析了Z模型和现金流量模型对企业财务危机预测的准确率，结果发现现金流量模型的预测效果较好。由于我国特有的破产制度以及数据获得的困难，企业财务危机预测研究起步较晚。目前国内对上市公司财务危机预警多以Z－Score多元判别分析(MDA)模型、逻辑回归模型和主成分分析等传统的统计模型以及神经网络等人工智能模型为主［1］。虽然这些模型具有较强的泛化与容错性能，却都存在前提条件过于苛刻、过学习等问题，预测效果不甚理想。

为了提高上市公司财务危机预测的精度，笔者将自组织数据挖掘(self－organize data mining，SODM)引入上市公司财务危机预测，自组织数据挖掘在处理噪声数据、数据降维和非线性建模等方面具有非常明显的优势，有望为上市公司财务危机预测提供新的研究途径和技术手段。

1 上市公司财务危机预测指标选取

由于研究目的不同或者研究时期的不同，研究者对财务危机的定义也不尽相同。在实证研究中，西方研究多将破产公司或申请破产的公司作为危机样本组。由于我国资本市场的特殊性，上市公司破产、退市案例比较少见，因此很难参照国外在实证研究中对上市公司财务危机进行界定。目前国内绝大多数实证研究都是将ST公司作为财务危机的研究样本。而大部分ST公司都是通过大规模的资产重组才恢复正常营运，证明ST公司确实陷入了财务危机。因此，参照国内相关研究文献，将因“财务状况异常”遭到“特别处理”的上市公司(ST公司)认定为发生财务危机的公司。

借鉴文献［2－7］的相关研究成果，笔者从公司盈利能力、偿债能力、成长能力、营运能力和现金流量这5个方面选择预测指标。

盈利能力是上市公司生存和发展的基石。盈利能力越强，发展潜力越大，发生财务危机的可能性越小。偿债能力反映公司能否健康生存和发展。如果上市公司无法到期偿还债务，则发生财务危机的可能性就会增加。成长能力反映上市公司未来的变化趋势和发展方向。营运能力反映上市公司的经营状况。现金流量情况反映上市公司的创造现金净流量能力、筹资能力和资金实力。考虑到数据的可获得性，构建了如表1所示的上市公司财务危机预测指标体系。

表1 上市公司财务危机预测指标体系

为加快运行效率，必须对上市公司财务数据进行分析，识别与财务危机相关的关键属性，在此基础上建立上市公司财务危机预测模型。笔者采用自组织数据挖掘算法中的客观系统分析方法(objective system analysis，OSA)来提取关键属性［8］。

基于OSA算法的基本原理，构建上市公司财务危机关键属性的选择算法，其步骤如下:

(1)将上市公司财务数据集W分成样本容量相同的两组A和B，使得W=A∪B。记A和B的数据长度均为 N。记 P={1，2，…，m}，Q={1，2，…，N}。

(2)令k=1。对第i个变量，用最小二乘法在样本全集上进行参数估计，可得到:

xi=a0+bx0i∈P

然后分别在数据集A和B上用最小二乘法进行参数估计，从而得到:

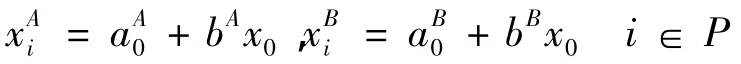
计算最小偏差准则值:

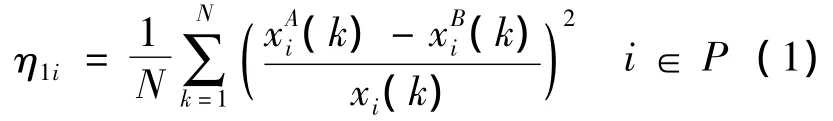
记η1=min(η1i)。

(3)令k=k+1。

在m个自变量中，任取k个不同的属性变量xi，xj，…，xr(i，j，…，r∈P)，用最小二乘法在样本全集上进行参数估计，得到k元方程组:

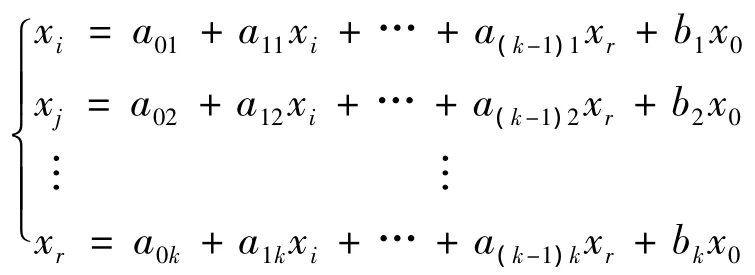
然后，对 xi，xj，…，xr(i，j，…，r∈P)用最小二乘法分别在集A，B上进行参数估计，得到:

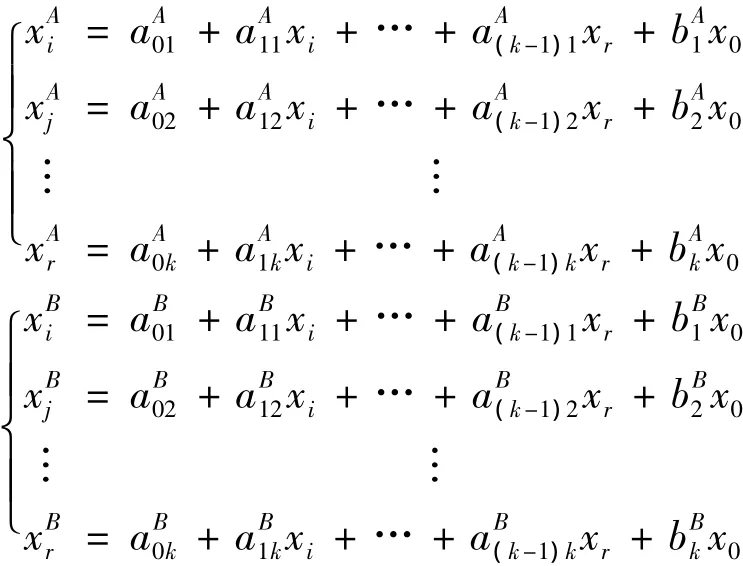
对每一个方程组计算最小偏差准则值:

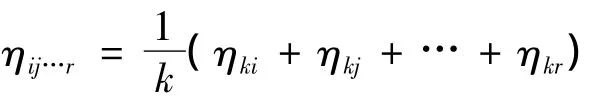
其中，ηki，ηkj，…，ηkr均按照式(1)计算得到。记 ηk=min(ηij…r)。

(4)比较 ηk与 ηk－1，若 ηk≤ηk－1，回到步骤(3);否则停止算法，记系统最小偏差准则值bestη=ηk－1。最小偏差准则值为 ηk－1时对应的方程组中的变量即为系统的特征变量。这些特征变量所对应的属性，即为判定上市公司是否将会发生财务危机的关键属性。

2 FRI上市公司财务危机预测

作为自组织数据挖掘的重要组成部分，自组织模糊规则归纳(fuzzy rule induction，FRI)算法使用黑箱方法分析处理系统输入与输出变量之间的关系，运用数据分组处理技术(GMDH)从系统已知的输入输出数据中自动地提取接近于人类自然语言的模糊规则，在提供预测结果的同时，具有很强的可解释性［9］。目前，FRI算法在复杂系统预测方面已取得了较好的应用效果，但现有文献鲜有将之应用于上市公司财务危机预测研究中。

FRI运用算法GMDH技术自动建立模糊模型的过程，实质上是应用模糊推理系统建立输入变量的真实值函数的过程。FRI模糊推理过程为模糊化→模糊推理(规则归纳)→逆模糊化→y，其中为系统的原始多变量输入，y为原始单变量输出。

模糊化。即通过隶属函数，将清晰变量x转化为模糊变量。笔者将各输入变量的取值范围分成重叠的等距区间，各模糊子集的隶属函数取均匀型分布函数(如图1所示)，将取值范围为［－b，b］的清晰输入变量x划分成负大(NB)、负小(NS)、零(Z)、正小(PS)、正大(PB)5个分区，它们对应的论域依次是(－∞，－a)，(－b，0］，［－a，a］，(0，b］，(a，∞ )，每个分区的中点为该分区的样板点，即此处的隶属度为1。则清晰输入变量 x 转化为模糊输入变量(x1，x2，x3，x4，x5)，其中 x1，x2，x3，x4，x5依次为变量 x 对应 NB、NS、Z、PS和PB的隶属度。

图1 隶属函数

笔者进行模糊化处理的具体过程为:

首先，确定零(Z)分区的代表点，即零点。一般情况下是用变量均值作为零点的。为了减小某些异常数据对模型准确度的影响，去掉每个变量的最小值min xi和最大值max xi，以其余数值的均值averxi作为零点。

然后，令 d=min(averxi－ min xi，max xi－averxi)，L=round(averxi－d)，U=round(averxi+d)，则变量的取值范围为［L，U］。与图1对应，－b→L，－ a→(L+averxi)/2，0→ averxi，a→ (U+averxi)/2，b→ U。

采用上述方法，可将输入变量xi转化成m个模糊集上的模糊数，输出变量y转化为 p个模糊集上的模糊数(y1，y2，…，yp)。

规则归纳。每个模糊规则都由前提(IF)部分和结果(THEN)部分组成。前提部分的模糊集称为输入模糊集，结果部分的模糊集称为输出模糊集。每个模糊规则在输入、输出空间的局部区域(模糊集)上指定了一种映射。因此FRI建模的关键是选取相关的模糊输入和以最优个数的模糊规则建立模糊模型。

FRI是基于GMDH技术进行模糊规则提取的。GMDH是一种基于遗传算法与进化的演化方法，它依据给定的准则从一系列候选模型集合中挑选出较优模型，通过遗传、变异和筛选，产生很多具有不断增长复杂度的候选模型，直至模型在观察样本数据上产生过拟合为止［10］。FRI通常具有多层网络结构，如图2所示。

图2 FRI网络图

令输入变量xi的个数为n，将输入变量xi转化为m个模糊集上的模糊数，则第一层中作为初始输入元素的各输入变量的模糊集的个数为n×m。FRI提取模糊规则的过程为:

(1)初始化。令 g=0，r=0，err=+∞(实际运行中可依建模的具体情况取一个足够大的值)。

(2)令r=r+1。如果r≤p(p为输出变量y转化的模糊分量的个数)，则转到步骤(3)，否则算法结束。

(3)令g=g+1。运用模糊逻辑，对每一对模糊输入建立AND运算。采用极小极大推理方法进行模糊归纳。令模糊输入的数量为Fg－1，则有yr(i，j)=min(Xi，Xj)(i，j=1，2，…，Fg－1)。其中，Xi，Xj为第g层的两个模糊输入。

如当g=1时，模糊输入的个数为F0=n×m，即则

(5)若 errg≤err，则令 err=errg，将选出的 Fg个最优模糊模型作为输入元素，转到步骤(3);否则，对选出的Fg个模型进行两两析取运算，即令，其中为第g层的模糊输出。然后，按使预测值与实际值之间误差平方和最小的选择准则从中选出最优模糊模型，由此可得到最终模糊模型的第r个分量yr，并转到步骤(2)。

逆模糊化。用得到的模糊输出量yr(r=1，2，…，m)对输出变量y进行拟合，得到最终模型y=f(y1，y2，…，yp)。

3 实证分析

从锐思金融研究数据库中，随机选取100家ST公司的数据和100家非ST公司的数据建立模型。从这200家上市公司中随机取80家ST公司的数据和80家非ST公司的数据作为学习样本集W1，剩余40家公司作为测试样本集W2。

以表1中的25个指标作为输入变量，上司公司财务状况(y)为目标变量，用0表示ST公司，1表示非ST公司。首先提取的关键变量有净资产收益率x1、成本费用利润率x2、利息保障倍数x3、现金流动负债比率x4、净资产增长率x5和经营活动产生的现金流量净额x6，以此建立基于FRI上市公司财务危机预测模型。根据我国上市公司的年报披露制度，上市公司当年的财务报告披露的最后截止日期为下一年4月30日，因此上市公司当年是否被ST是由公司上年的财务报表决定的，采用公司刚好被ST前的数据来建立预测模型没有实际的预测意义。因此，笔者采用上市公司被ST前2年的数据来进行实证分析。

利用FRI算法，将输入变量xi转化为5个模糊集上的模糊数，输出变量y因为已经是类别数据，故不用再转化，以y=(y0，y1)来表示上市公司财务危机状态，其中y0和y1分别为公司属于ST类和非ST类的隶属度。分别取F1=14、26和38，在W1上进行训练，结果显示当F1=38时模型在训练集上的误差平方和最小。此时筛选出如下两条规则:

判别规则:如果 y≥0．5，则认为该公司短期内不会发生财务危机，否则认为该公司将发生财务危机。

利用上述判别规则对W2进行检验，结果如表2所示。

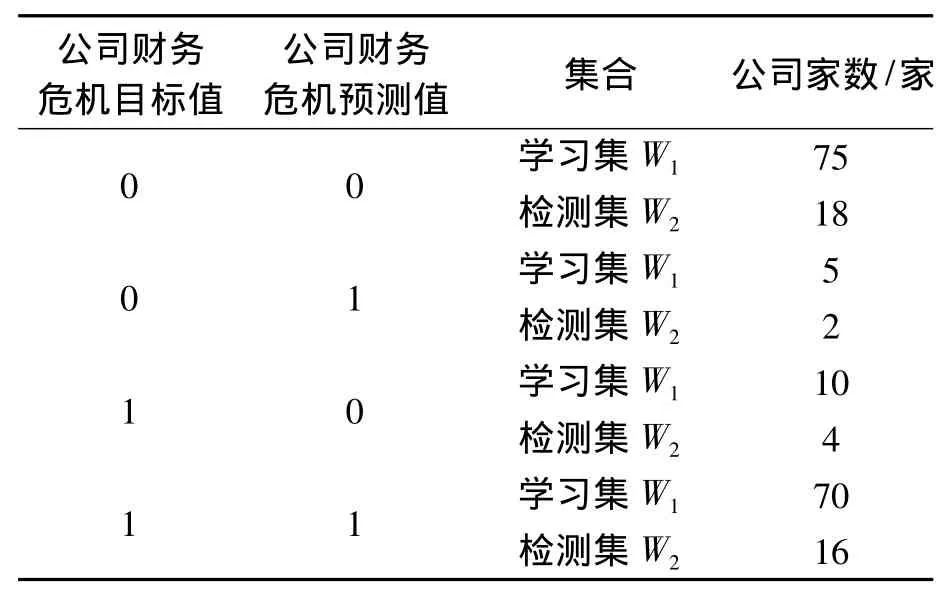
表2 上市公司财务危机预测结果

由表2可以看出，模型学习集和检测集的总体分类准确率分别为(75+70)/160=90．6%和(18+16)/40=85．0%，对ST公司的识别率分别为75/80=93．8%和 18/20=90．0%，对非 ST 公司的识别率分别为70/80=87．5%和16/20=80．0%。将非ST公司误判为ST公司的概率高于将ST公司误判为非ST公司的概率。但不论学习集还是检测集的误判率均在20%以下，判定正确率比较理想。

4 结论

(1)利用OSA算法对上市公司财务属性变量进行选择，在不损失信息的前提下得到6个关键属性分别是资产收益率x1、成本费用利润率x2、利息保障倍数x3、现金流动负债比率x4、净资产增长率x5和经营活动产生的现金流量净额x6，使得GMDH网络输入端数据数量大大减少，简化了网络结构，提高了网络系统的预测速度和学习效率。

(2)把FRI网络作为后置的信息处理系统，提高了模型的容错和抗干扰能力。用FRI网络对经约简后的样本数据进行训练，并从训练样本中提取出了2条上市公司财务危机判断规则，学习集预测准确率达到90．6%，检测集预测准确率也达到85．0%。这说明该模型在上市公司财务危机预测上有广泛的应用前景。

(3)该模型也存在一些不足，如将非ST公司误判为ST的数量较大，如何进一步提高模型对上市公司财务危机预测的能力将是后续研究的重要内容之一。

［1］ 谢邦昌，么海亮．基于穷尽CHAID算法的中国上市公司财务危机模型［J］．统计与决策，2013(1):83 －85．

［2］ 黄迅，张颖，林宇．中国海外上市公司的PCA－SVM财务危机预警研究［J］．成都理工大学学报:社会科学版，2013(1):92－100．

［3］ 周喜，吴可夫．基于混合粗糙集与ANN的上市公司财务危机预警研究［J］．企业经济，2012(2):37－40．

［4］ 潘彬，凌飞．引入违约距离的上市公司财务危机预警应用［J］．系统工程，2012(3):45－51．

［5］ 卢永艳，王维国．基于财务状况多分类的上市公司财务危机预警［J］．数学的实践与认识，2011，41(4):27－33．

［6］ 王智宁，吴应宇，叶新凤．基于Pulic智力资本模型的上市公司财务危机预警研究［J］．数理统计与管理，2009，28(2):309 －317．

［7］ 曹珊珊．上市公司财务困境预测:基于信息熵与Logistic回归的实证分析［J］．对外经贸，2012(9):149－152．

［8］ 张秋菊，朱帮助．基于自组织数据挖掘的电子商务客户流失预测模型［J］．企业经济，2011(1):95－99．

［9］ 刘学生，何跃，贺昌政．模糊规则归纳法及GDP主要影响因素分析［J］．电子科技大学学报，2002，32(1):92－96．

［10］ 贺昌政．自组织数据挖掘与经济预测［M］．北京:科学出版社，2005:43－98．